2021-2022学年人教版九年级数学上册 23.1 图形的旋转 同步练习题 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册 23.1 图形的旋转 同步练习题 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 499.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 14:53:52 | ||
图片预览



文档简介
2021——2022学年度人教版九年级数学上册 第二十三章 旋转 23.1 图形的旋转 同步练习题
一、选择题
1.如图,△ABC按顺时针旋转到△ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点 B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点 D.点D是旋转中心,点A和点D是对应点
2.如图, 将 绕点顺时针旋转一定的角度与 重合 与 是对应点 , 使得点恰好落在上, 若, 则 的度数为 ( )
A. B. C. D.
3.如图,RtABC中,∠C=90°,AC=4,BC=3,以B点为中心,将ABC旋转至DBE,使E点恰好在AB上,则AE的长为( )
A.1 B.2 C.3 D.4
4.如图,∠ABC=20°,将△ABC绕点B顺时针旋转130°得到△EBF.若点A,F,E在同一条直线上,则∠AFB的度数是( )
A.35° B.40° C.45° D.50°
5.如图,是正方形内一点,以为一条边作正方形,连接和.根据旋转知识,给出下列四个说法:①;②; ③若点恰好落在边上时,则; ④若,则.其中正确说法的个数是( )
A.4个 B.3个 C.2个 D.1个
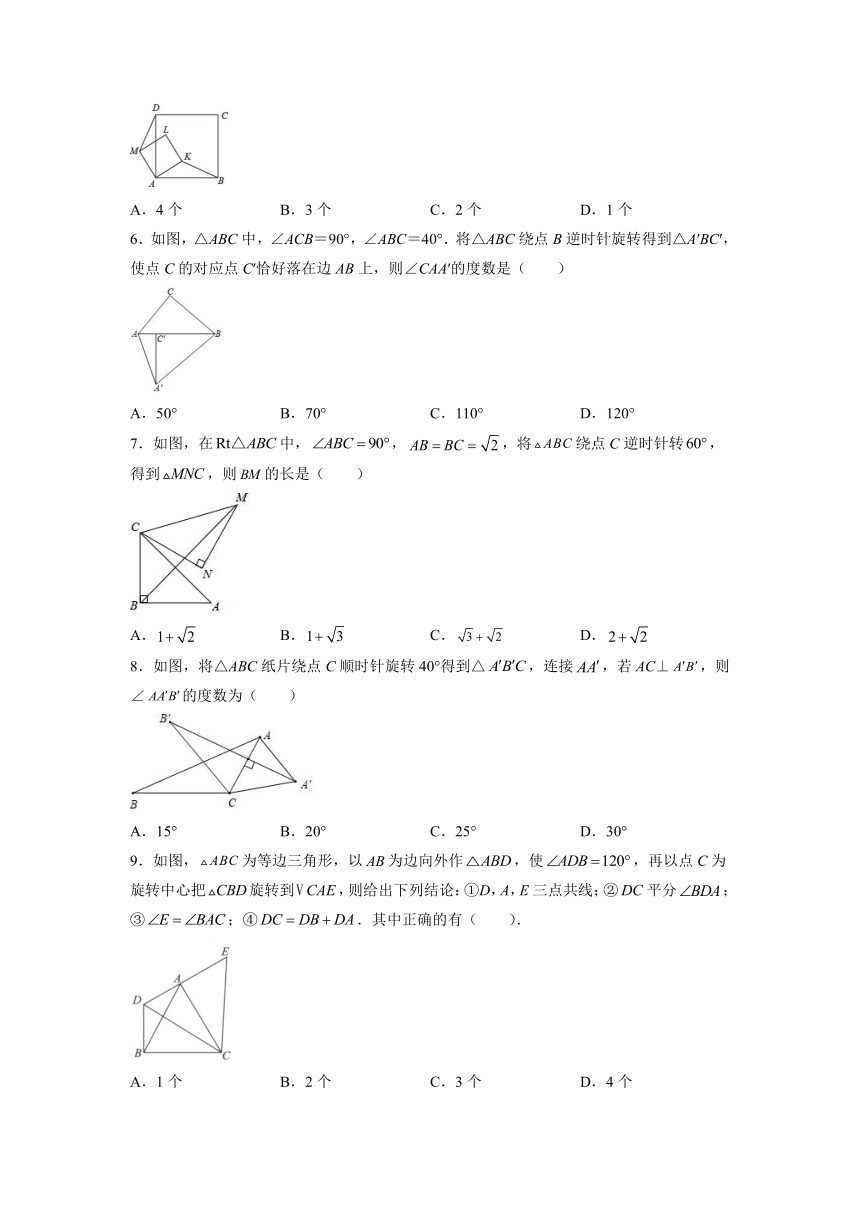
6.如图,△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( )
A.50° B.70° C.110° D.120°
7.如图,在中,,,将绕点C逆时针转,得到,则的长是( )
A. B. C. D.
8.如图,将△ABC纸片绕点C顺时针旋转40°得到△,连接,若AC⊥,则∠的度数为( )
A.15° B.20° C.25° D.30°
9.如图,为等边三角形,以为边向外作,使,再以点C为旋转中心把旋转到,则给出下列结论:①D,A,E三点共线;②平分;③;④.其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
10.如图,在△ABC中,∠ACB=105°,将△ABC绕着点C顺时针方向旋转到△,经过点 A.若=AC,则∠B的度数为( )
A.20° B.25° C.30° D.35°
二、填空题
11.如图,中,,点A的坐标为,点B在x轴上,将绕点B按顺时针方向旋转后得,点A的对应点在x轴上,点的坐标为________.
12.如图,平面内三点A、B、C,AB=5,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD的最大值是__________.
13.如图,绕点A旋转得到,点C恰好落在线段上,已知,则________度.
14.如图,C为线段AB的中点,D为AB垂直平分线上一点,连接BD,将BD绕点D顺时针旋转60°得到线段DE,连接AE,若AB=2,AE=4,则CD的长为 ___.
15.如图,将△ABC绕点A顺时针旋转角α(0°<α<180°),得到△AED,若AC=1,CE=,则α的度数为 ___.
三、解答题
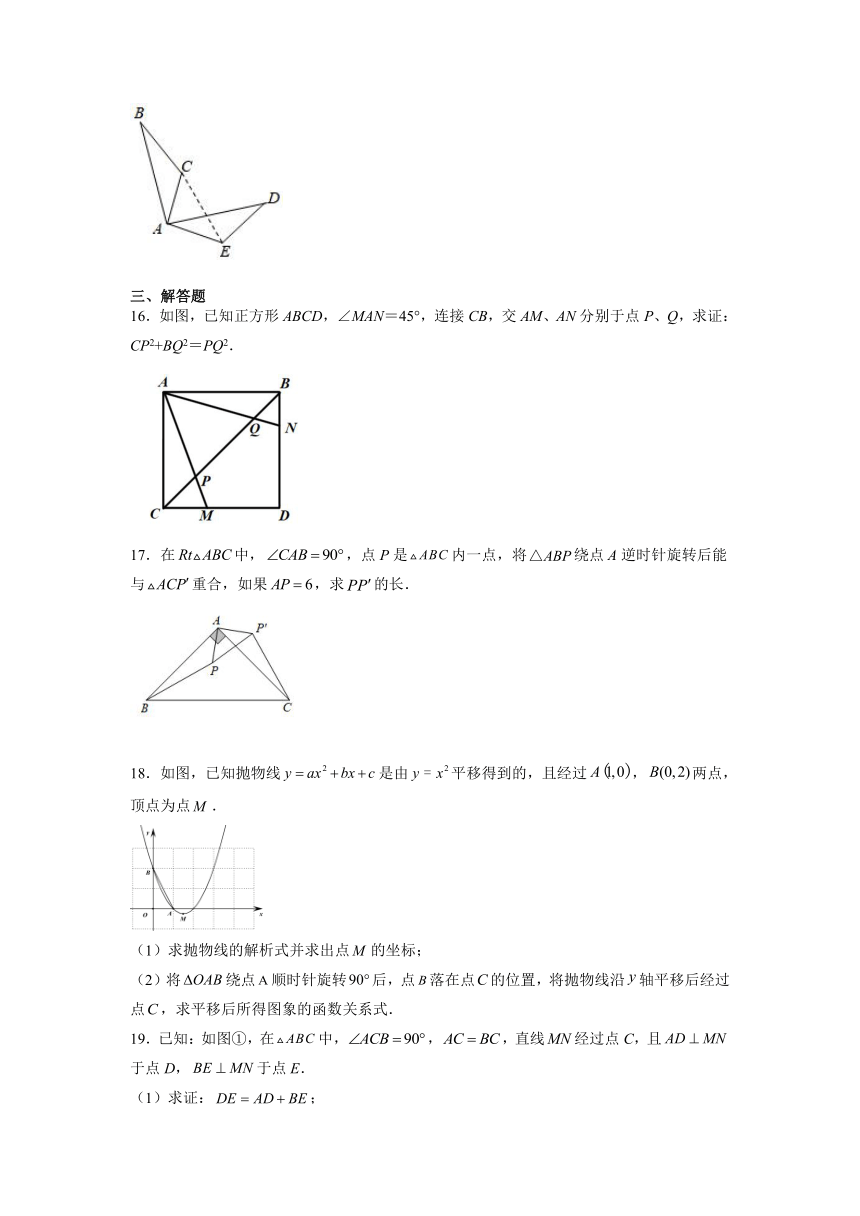
16.如图,已知正方形ABCD,∠MAN=45°,连接CB,交AM、AN分别于点P、Q,求证:CP2+BQ2=PQ2.
17.在中,,点P是内一点,将绕点A逆时针旋转后能与重合,如果,求的长.
18.如图,已知抛物线是由平移得到的,且经过,两点,顶点为点.
(1)求抛物线的解析式并求出点的坐标;
(2)将绕点顺时针旋转后,点落在点的位置,将抛物线沿轴平移后经过点,求平移后所得图象的函数关系式.
19.已知:如图①,在中,,,直线经过点C,且于点D,于点E.
(1)求证:;
(2)当直线绕点C旋转到图②位置时,、、之间有怎样的等量关系?请写出这个等量关系,并加以证明,
20.在平面直角坐标系中,为原点,点,点,把绕点顺时针旋转,得,点,旋转后的对应点为,.
(1)如图①,当旋转角为时,求的长;
(2)如图②,当旋转角为时,求点的坐标;
(3)在(2)的条件下,边上的一点旋转后的对应点为,当取得最小值时,求点的坐标_______.(直接写出结果即可)
21.综合与实践
(情境呈现)如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°.若固定△ABC,将△DEC绕着点C旋转.
(初步探究)(1)如图2,当△DEC绕点C旋转,点D恰好落在AB边的中点上时,请求出此时旋转角的度数.
(2)如图2,当△DEC绕点C旋转,点D恰好落在AB边上时,若此时旋转角为,则∠CED的度数为 (用含的式子表示) .
(拓展提升)(3)当△DEC绕点C旋转到如图3所示的位置时,勤勉小组猜想:△BDC的面积与△AEC的面积相等,试判断勤勉小组的猜想是否正确,若正确,请你帮他们证明;若不正确,请说明理由.
22.如图,是等腰直角三角形,,,点是线段上的一个动点,连接,将线段绕点顺时针旋转至点,连接交于点.
(1)连接,求证:;
(2)当时,判断是什么三角形?并说明理由;
(3)在点运动过程中,当是锐角三角形时,求的取值范围.
23.如图1,在正方形ABCD中,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连接EF.
(1)思路梳理:将ABE绕点A逆时针旋转至ADG,如图1,使AB与AD重合,易证∠GAF=∠EAF=45°,可证AFG≌AFE,故EF,BE,DF之间的数量关系为 ;
(2)类比引申:如图2,在图1的条件下,若点E,F由原来的位置分别变到正方形ABCD的边CB,DC的延长线上,∠EAF=45°,连接EF,猜想EF,BE,DF之间的数量关系为 ,并给出证明;
(3)联想拓展:如图3,等腰RtABC,∠BAC=90°,∠MAN=45°,把∠MAN绕点A旋转,在整个旋转过程中AM、AN分别与直线BC交于点D、E,若BD=2,EC=4,则BE的长为 .
【参考答案】
1.C 2.B 3.B 4.C 5.B 6.D 7.B 8.B 9.D 10.B
11.
12.
13.40
14.7
15.
16.证明:将△ABQ绕A点顺时针旋转90°得到△ACQ′,连接PQ′,
∴AQ′=AQ,CQ′=BQ,∠BAQ=∠CAQ′,∠ACQ′=∠ABC,
∵四边形ABCD为正方形,
∴∠ACQ′=∠ABC=∠ACB=45°,∠CAB=90°,
∵∠MAN=45°,
∴∠CAP+∠BAQ=45°,
∴∠Q′AP=∠CAQ′+∠CAP=45°,
∴∠Q′AP=∠QAP,
在△Q′AP和△QAP中,
,
∴△Q′AP≌△QAP(SAS),
∴PQ=PQ′,
∵∠Q′CP=∠ACQ′+∠ACB=90°,
在Rt△Q′CP中,由勾股定理得,
Q′P2=Q′C2+CP2,
∴CP2+BQ2=PQ2.
17.解:∵将△ABP绕点A逆时针旋转后能与△ACP′重合,
∴△ABP≌△ACP'.
∴AP=AP=6,∠BAP=∠CAP'.
∵∠BAC=90°,
∴∠BAP+∠CAP=90°.
∴∠CAP′+∠CAP=90°,
即∠PAP'=90°.
∴△PAP′是等腰直角三角形.
由勾股定理得: .
∴PP′的长为.
18.解:(1)∵是由平移得到
∴抛物线y=x2+bx+c
∵经过A(1,0),B(0,2),
∴,
解得,
∴所求抛物线的解析式为y=x2﹣3x+2;
∴顶点坐标为M:
(2)∵A(1,0),B(0,2),
∴OA=1,OB=2,
由旋转可得OA=CD=1,OB=AD=2
∴C点的坐标为(3,1),
当x=3时,由y=x2﹣3x+2得y=2,
可知抛物线y=x2﹣3x+2过点(3,2),
∴将原抛物线沿y轴向下平移1个单位后过点C.
∴平移后的抛物线解析式为:y=x2﹣3x+1;
19.(1)证明:,
,而于,于,
,,
,
在和中,
,
,
,,
;
(2),
在和中,
,
,
,,
.
20.(1);(2) ;(3)
21.(1) 由旋转可知:CA=CD
∵∠A=90°,D是AB的中点
∴CD=AD
∴CA=CD=AD
∴△ACD是等边三角形
∴∠ACD=60°
∴旋转角为60°
(2) ,理由如下:
由旋转性质知AC=DC,故∠ACD=,∠A=∠ADC=,
又∵∠CDE=∠A=,
∴∠CED=
(3)勤勉小组的猜想是正确的
理由如下:
过点D作DH⊥BC,垂足为H,
过点A作AG⊥EC的延长线于点G,如图3
∵∠ACB=∠DCE=90°
∴∠HCD+∠ACE=180°
∵∠ACE+∠GCA=180°
∴∠HCD=∠GCA
∵DH⊥BC ,AG⊥EC
∴∠DHC=∠AGC=90°
由旋转可得:CD=CA
∴在△DHC和△AGC中
∴△DHC≌△AGC(AAS)
∴DH=AG
∵,,BC=EC
∴
22.(1)∵是等腰直角三角形,
∴AC=BC,∠ACB=90°
∵将线段绕点顺时针旋转至点,
∴CD=CE,∠DCE=90°
∴∠ACD+∠DCF=∠BCE+∠DCF=90°
∴∠ACD=∠BCE
∴(SAS)
(2)是直角三角形,理由如下:
∵,∠HAC=30°
∴∠ACD=180°-15°-30°=135°
∵
∴∠BEC=∠ACD=135°
∵将线段绕点顺时针旋转至点,
∴CD=CE,∠DCE=90°
∴△ECD是等腰直角三角形
∴∠CED=45°
∴∠BEF=135°-45°=90°
∴是直角三角形;
(3)由(2)得当时, 是直角三角形,此时BE⊥EF;
如图,当AF⊥BF时,∠EFB=90°
∵△ECD是等腰直角三角形,∠CED=45°
∴∠ECF=90°-45°=45°
故=∠ECF=∠ACD=45°
∵点是线段上的一个动点,故AB不能与BF垂直,
∴当是锐角三角形时,求的取值范围为15°<<45°.
23.解:(1)如图1所示:
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
∴∠DAG=∠BAE,AE=AG,
∴∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=90°-45°=45°=∠EAF,即∠EAF=∠FAG.
在△EAF和△GAF中,
,
∴△AFG≌△AFE(SAS).
∴EF=FG.
∴EF=DF+DG=DF+BE,即EF=BE+DF.
故答案为:BE+FD=EF;
(2)DF=EF+BE.
证明:如图2所示.
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∵∠ADC=∠ABE=90°,
∴点C、D、G在一条直线上.
∴EB=DG,AE=AG,∠EAB=∠GAD.
又∵∠BAG+∠GAD=90°,
∴∠EAG=∠BAD=90°.
∵∠EAF=45°,
∴∠FAG=∠EAG-∠EAF=90°-45°=45°.
∴∠EAF=∠GAF.
在△EAF和△GAF中,
,
∴△EAF≌△GAF(SAS).
∴EF=FG.
∵FD=FG+DG,
∴DF=EF+BE,
故答案为:DF=EF+BE;
(3)把△ACE旋转到ABF的位置,连接DF,则∠FAB=∠CAE.
∵∠BAC=90°,∠DAE=45°,
∴∠BAD+∠CAE=45°,
又∵∠FAB=∠CAE,
∴∠FAD=∠DAE=45°,
则在△ADF和△ADE中,
,
∴△ADF≌△ADE(SAS).
∴DF=DE,∠C=∠ABF=45°.
∴∠BDF=90°.
∴△BDF是直角三角形.
∴BD2+BF2=DF2.
∴BD2+CE2=DE2.
∴DE=,
∴BE=BD+DE=,
故答案为:.
一、选择题
1.如图,△ABC按顺时针旋转到△ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点 B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点 D.点D是旋转中心,点A和点D是对应点
2.如图, 将 绕点顺时针旋转一定的角度与 重合 与 是对应点 , 使得点恰好落在上, 若, 则 的度数为 ( )
A. B. C. D.
3.如图,RtABC中,∠C=90°,AC=4,BC=3,以B点为中心,将ABC旋转至DBE,使E点恰好在AB上,则AE的长为( )
A.1 B.2 C.3 D.4
4.如图,∠ABC=20°,将△ABC绕点B顺时针旋转130°得到△EBF.若点A,F,E在同一条直线上,则∠AFB的度数是( )
A.35° B.40° C.45° D.50°
5.如图,是正方形内一点,以为一条边作正方形,连接和.根据旋转知识,给出下列四个说法:①;②; ③若点恰好落在边上时,则; ④若,则.其中正确说法的个数是( )
A.4个 B.3个 C.2个 D.1个
6.如图,△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( )
A.50° B.70° C.110° D.120°
7.如图,在中,,,将绕点C逆时针转,得到,则的长是( )
A. B. C. D.
8.如图,将△ABC纸片绕点C顺时针旋转40°得到△,连接,若AC⊥,则∠的度数为( )
A.15° B.20° C.25° D.30°
9.如图,为等边三角形,以为边向外作,使,再以点C为旋转中心把旋转到,则给出下列结论:①D,A,E三点共线;②平分;③;④.其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
10.如图,在△ABC中,∠ACB=105°,将△ABC绕着点C顺时针方向旋转到△,经过点 A.若=AC,则∠B的度数为( )
A.20° B.25° C.30° D.35°
二、填空题
11.如图,中,,点A的坐标为,点B在x轴上,将绕点B按顺时针方向旋转后得,点A的对应点在x轴上,点的坐标为________.
12.如图,平面内三点A、B、C,AB=5,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD的最大值是__________.
13.如图,绕点A旋转得到,点C恰好落在线段上,已知,则________度.
14.如图,C为线段AB的中点,D为AB垂直平分线上一点,连接BD,将BD绕点D顺时针旋转60°得到线段DE,连接AE,若AB=2,AE=4,则CD的长为 ___.
15.如图,将△ABC绕点A顺时针旋转角α(0°<α<180°),得到△AED,若AC=1,CE=,则α的度数为 ___.
三、解答题
16.如图,已知正方形ABCD,∠MAN=45°,连接CB,交AM、AN分别于点P、Q,求证:CP2+BQ2=PQ2.
17.在中,,点P是内一点,将绕点A逆时针旋转后能与重合,如果,求的长.
18.如图,已知抛物线是由平移得到的,且经过,两点,顶点为点.
(1)求抛物线的解析式并求出点的坐标;
(2)将绕点顺时针旋转后,点落在点的位置,将抛物线沿轴平移后经过点,求平移后所得图象的函数关系式.
19.已知:如图①,在中,,,直线经过点C,且于点D,于点E.
(1)求证:;
(2)当直线绕点C旋转到图②位置时,、、之间有怎样的等量关系?请写出这个等量关系,并加以证明,
20.在平面直角坐标系中,为原点,点,点,把绕点顺时针旋转,得,点,旋转后的对应点为,.
(1)如图①,当旋转角为时,求的长;
(2)如图②,当旋转角为时,求点的坐标;
(3)在(2)的条件下,边上的一点旋转后的对应点为,当取得最小值时,求点的坐标_______.(直接写出结果即可)
21.综合与实践
(情境呈现)如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°.若固定△ABC,将△DEC绕着点C旋转.
(初步探究)(1)如图2,当△DEC绕点C旋转,点D恰好落在AB边的中点上时,请求出此时旋转角的度数.
(2)如图2,当△DEC绕点C旋转,点D恰好落在AB边上时,若此时旋转角为,则∠CED的度数为 (用含的式子表示) .
(拓展提升)(3)当△DEC绕点C旋转到如图3所示的位置时,勤勉小组猜想:△BDC的面积与△AEC的面积相等,试判断勤勉小组的猜想是否正确,若正确,请你帮他们证明;若不正确,请说明理由.
22.如图,是等腰直角三角形,,,点是线段上的一个动点,连接,将线段绕点顺时针旋转至点,连接交于点.
(1)连接,求证:;
(2)当时,判断是什么三角形?并说明理由;
(3)在点运动过程中,当是锐角三角形时,求的取值范围.
23.如图1,在正方形ABCD中,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连接EF.
(1)思路梳理:将ABE绕点A逆时针旋转至ADG,如图1,使AB与AD重合,易证∠GAF=∠EAF=45°,可证AFG≌AFE,故EF,BE,DF之间的数量关系为 ;
(2)类比引申:如图2,在图1的条件下,若点E,F由原来的位置分别变到正方形ABCD的边CB,DC的延长线上,∠EAF=45°,连接EF,猜想EF,BE,DF之间的数量关系为 ,并给出证明;
(3)联想拓展:如图3,等腰RtABC,∠BAC=90°,∠MAN=45°,把∠MAN绕点A旋转,在整个旋转过程中AM、AN分别与直线BC交于点D、E,若BD=2,EC=4,则BE的长为 .
【参考答案】
1.C 2.B 3.B 4.C 5.B 6.D 7.B 8.B 9.D 10.B
11.
12.
13.40
14.7
15.
16.证明:将△ABQ绕A点顺时针旋转90°得到△ACQ′,连接PQ′,
∴AQ′=AQ,CQ′=BQ,∠BAQ=∠CAQ′,∠ACQ′=∠ABC,
∵四边形ABCD为正方形,
∴∠ACQ′=∠ABC=∠ACB=45°,∠CAB=90°,
∵∠MAN=45°,
∴∠CAP+∠BAQ=45°,
∴∠Q′AP=∠CAQ′+∠CAP=45°,
∴∠Q′AP=∠QAP,
在△Q′AP和△QAP中,
,
∴△Q′AP≌△QAP(SAS),
∴PQ=PQ′,
∵∠Q′CP=∠ACQ′+∠ACB=90°,
在Rt△Q′CP中,由勾股定理得,
Q′P2=Q′C2+CP2,
∴CP2+BQ2=PQ2.
17.解:∵将△ABP绕点A逆时针旋转后能与△ACP′重合,
∴△ABP≌△ACP'.
∴AP=AP=6,∠BAP=∠CAP'.
∵∠BAC=90°,
∴∠BAP+∠CAP=90°.
∴∠CAP′+∠CAP=90°,
即∠PAP'=90°.
∴△PAP′是等腰直角三角形.
由勾股定理得: .
∴PP′的长为.
18.解:(1)∵是由平移得到
∴抛物线y=x2+bx+c
∵经过A(1,0),B(0,2),
∴,
解得,
∴所求抛物线的解析式为y=x2﹣3x+2;
∴顶点坐标为M:
(2)∵A(1,0),B(0,2),
∴OA=1,OB=2,
由旋转可得OA=CD=1,OB=AD=2
∴C点的坐标为(3,1),
当x=3时,由y=x2﹣3x+2得y=2,
可知抛物线y=x2﹣3x+2过点(3,2),
∴将原抛物线沿y轴向下平移1个单位后过点C.
∴平移后的抛物线解析式为:y=x2﹣3x+1;
19.(1)证明:,
,而于,于,
,,
,
在和中,
,
,
,,
;
(2),
在和中,
,
,
,,
.
20.(1);(2) ;(3)
21.(1) 由旋转可知:CA=CD
∵∠A=90°,D是AB的中点
∴CD=AD
∴CA=CD=AD
∴△ACD是等边三角形
∴∠ACD=60°
∴旋转角为60°
(2) ,理由如下:
由旋转性质知AC=DC,故∠ACD=,∠A=∠ADC=,
又∵∠CDE=∠A=,
∴∠CED=
(3)勤勉小组的猜想是正确的
理由如下:
过点D作DH⊥BC,垂足为H,
过点A作AG⊥EC的延长线于点G,如图3
∵∠ACB=∠DCE=90°
∴∠HCD+∠ACE=180°
∵∠ACE+∠GCA=180°
∴∠HCD=∠GCA
∵DH⊥BC ,AG⊥EC
∴∠DHC=∠AGC=90°
由旋转可得:CD=CA
∴在△DHC和△AGC中
∴△DHC≌△AGC(AAS)
∴DH=AG
∵,,BC=EC
∴
22.(1)∵是等腰直角三角形,
∴AC=BC,∠ACB=90°
∵将线段绕点顺时针旋转至点,
∴CD=CE,∠DCE=90°
∴∠ACD+∠DCF=∠BCE+∠DCF=90°
∴∠ACD=∠BCE
∴(SAS)
(2)是直角三角形,理由如下:
∵,∠HAC=30°
∴∠ACD=180°-15°-30°=135°
∵
∴∠BEC=∠ACD=135°
∵将线段绕点顺时针旋转至点,
∴CD=CE,∠DCE=90°
∴△ECD是等腰直角三角形
∴∠CED=45°
∴∠BEF=135°-45°=90°
∴是直角三角形;
(3)由(2)得当时, 是直角三角形,此时BE⊥EF;
如图,当AF⊥BF时,∠EFB=90°
∵△ECD是等腰直角三角形,∠CED=45°
∴∠ECF=90°-45°=45°
故=∠ECF=∠ACD=45°
∵点是线段上的一个动点,故AB不能与BF垂直,
∴当是锐角三角形时,求的取值范围为15°<<45°.
23.解:(1)如图1所示:
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
∴∠DAG=∠BAE,AE=AG,
∴∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=90°-45°=45°=∠EAF,即∠EAF=∠FAG.
在△EAF和△GAF中,
,
∴△AFG≌△AFE(SAS).
∴EF=FG.
∴EF=DF+DG=DF+BE,即EF=BE+DF.
故答案为:BE+FD=EF;
(2)DF=EF+BE.
证明:如图2所示.
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∵∠ADC=∠ABE=90°,
∴点C、D、G在一条直线上.
∴EB=DG,AE=AG,∠EAB=∠GAD.
又∵∠BAG+∠GAD=90°,
∴∠EAG=∠BAD=90°.
∵∠EAF=45°,
∴∠FAG=∠EAG-∠EAF=90°-45°=45°.
∴∠EAF=∠GAF.
在△EAF和△GAF中,
,
∴△EAF≌△GAF(SAS).
∴EF=FG.
∵FD=FG+DG,
∴DF=EF+BE,
故答案为:DF=EF+BE;
(3)把△ACE旋转到ABF的位置,连接DF,则∠FAB=∠CAE.
∵∠BAC=90°,∠DAE=45°,
∴∠BAD+∠CAE=45°,
又∵∠FAB=∠CAE,
∴∠FAD=∠DAE=45°,
则在△ADF和△ADE中,
,
∴△ADF≌△ADE(SAS).
∴DF=DE,∠C=∠ABF=45°.
∴∠BDF=90°.
∴△BDF是直角三角形.
∴BD2+BF2=DF2.
∴BD2+CE2=DE2.
∴DE=,
∴BE=BD+DE=,
故答案为:.
同课章节目录
