2021-2022学年人教版八年级数学上册《第14章整式的乘法与因式分解》单元综合优生辅导测试 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册《第14章整式的乘法与因式分解》单元综合优生辅导测试 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 811.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 10:19:03 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学上册《第14章整式的乘法与因式分解》
单元综合优生辅导测试(附答案)
一、单选题(满分30分)
1.下列等式中,从左到右的变形是因式分解的是( )
A. B.
C. D.
2.已知a、b满足等式,x=a2﹣6ab+9b2.y=4a﹣12b﹣4,则x,y的大小关系是( )
A.x=y B.x>y C.x<y D.x≥y
3.下列计算正确的是( )
A. B.
C. D.
4.如图,现有足够多的型号为①②③的正方形和长方形卡片,如果分别选取这三种型号卡片若干张,可以拼成一个不重叠、无缝隙的长方形,小星想用拼图前后面积之间的关系.解释多项式乘法,则其中②和③型号卡片需要的张数各是( )
A.3张和7张 B.2张和3张 C.5张和7张 D.2张和7张
5.已知a、b、c是三角形的边长,那么代数式的值是( )
A.小于零 B.等于零 C.大于零 D.大小不确定
6.已知长方形的周长为16cm,它两邻边长分别为xcm,ycm,且满足,则该长方形的面积为( )cm2
A. B. C.15 D.16
7.若的计算结果中项的系数为,则为( )
A. B. C. D.
8.已知,,则计算①;②;③中错误的个数是( )
A.0 B.1 C.2 D.3
9.已知,,,现给出3个实数a,b,c之间的四个关系式:①;②;③;④.其中,正确的关系式的个数是( )
A.1 B.2 C.3 D.4
10.计算(1)(1)……(1)(1)的值是( )
A. B. C. D.
二、填空题(满分30分)
11.长方形的面积为,长为,则它的周长为______________.
12.已知,则_____.
13.已知,,则______.
14.将边长为1的正方形纸片按如图所示方法进行对折,记第1次对折后得到的图形面积为S1,第2次对折后得到的图形面积为S2,…,第n次对折后得到的图形面积为Sn,请根据图2化简, ______.
15.若,,则______.
16.如图所示,长方形ABCD中放置两个边长都为5的正方形AEFG与正方形CHIJ,若如图阴影部分的面积之和记为,长方形ABCD的面积记为,已知:,则长方形ABCD的周长为______.
17.计算:______.
18.若是一个完全平方式,则__________.
19.已知,,,则________.
20.如图,点M是AB中点,点P在MB上,分别以AP,BP为边作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=6,ab=7,则图中阴影部分的面积为______.
三、解答题(满分60分)
21.若(x﹣2)(x2+ax﹣8b)的展开式中不含x的二次项和一次项.
(1)求b的值;
(2)求(a+1)(a2+1)(a4+1)…(a32+1)+1的值.
22.分解因式:
(1);(2).
23.分解因式:
(1); (2);
(3); (4).
24.阅读理解题
问题提出:如果一个正整数能表示为两个正整数的平方差,那么称这个正整数为“幸福数”.例如,,16就是一个幸福数.我们按照从小到大的顺序把“3,5,7,8,…,,…” 这些幸福数进行排列依次记为:第1个幸福数3,第2个幸福数5,第3个幸福数7,第4个幸福数8,…,第个幸福数.现在需要探究出一种判断一个较大的数是否是幸福数的方法;以及如何求出第个幸福数的值.
实践探究:小明的方法是:在正整数中,从1开始采取从小到大逐个排查的办法一个一个找出来:
,,,
,,,
…
(1)请将第10个幸福数仿照小明的方法用等式表示出来: ;
小颖认为小明的方法太麻烦,她想到:设是正整数,由于,所以,除1外,所有的奇数都是幸福数;又因为所以,除4外,所有能被4整除的偶数都是幸福数;小颖通过上面的探索,已经证明了形如、、(是正整数)的正整数都是幸福数.
(2)请证明形如(是正整数)的数不是幸福数;
迁移应用:(3)当时,求的值.
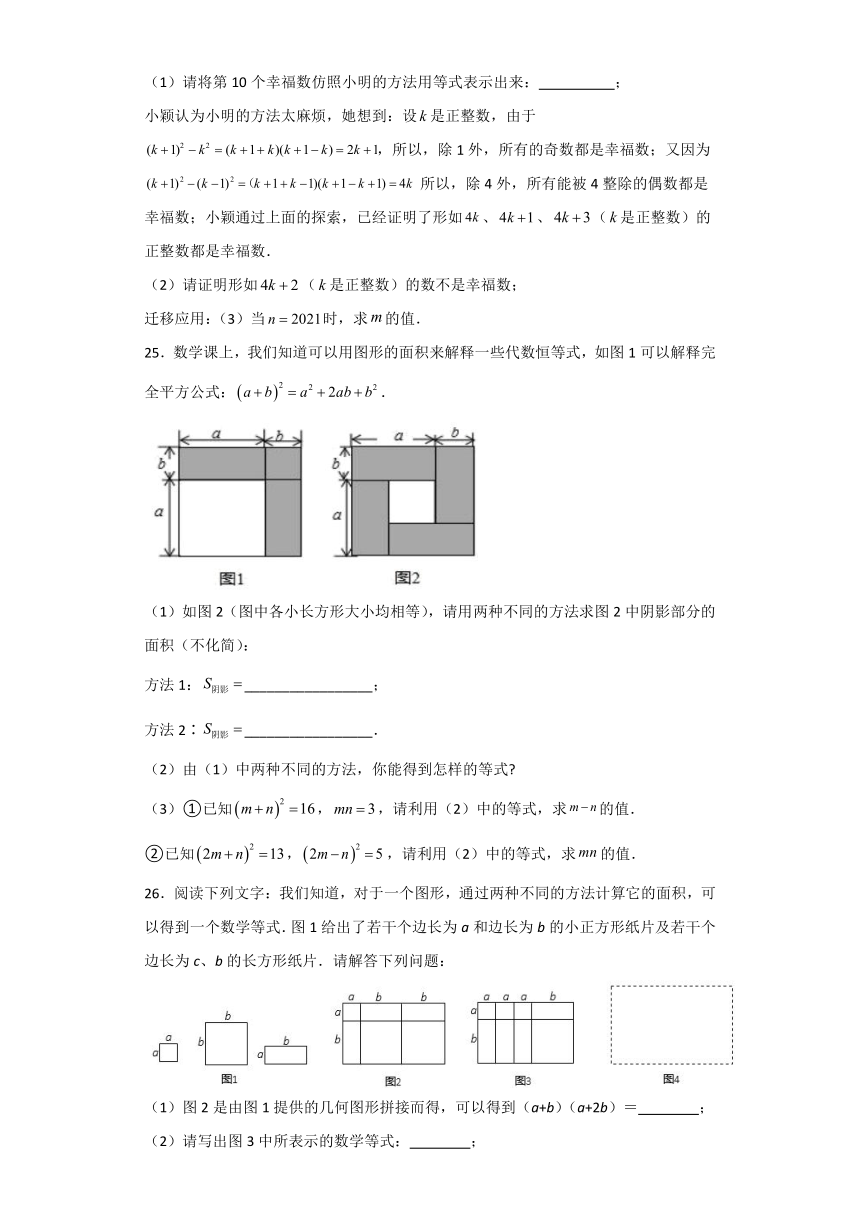
25.数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图1可以解释完全平方公式:.
(1)如图2(图中各小长方形大小均相等),请用两种不同的方法求图2中阴影部分的面积(不化简):
方法1:_________________;
方法2∶_________________.
(2)由(1)中两种不同的方法,你能得到怎样的等式
(3)①已知,,请利用(2)中的等式,求的值.
②已知,,请利用(2)中的等式,求的值.
26.阅读下列文字:我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.图1给出了若干个边长为a和边长为b的小正方形纸片及若干个边长为c、b的长方形纸片.请解答下列问题:
(1)图2是由图1提供的几何图形拼接而得,可以得到(a+b)(a+2b)= ;
(2)请写出图3中所表示的数学等式: ;
(3)请按要求利用所给的纸片在图4的方框中拼出一个长方形,要求所拼出图形的面积为(2a+b)(a+b),进而可以得到等式:(2a+b)(a+b)= .
(4)利用(3)中得到的结论,解决下面的问题:若4a2+6ab+2b2=5,a+b=,求2a+b的值.
参考答案
1.C
解:A、不是把一个多项式化为几个整式的积的形式,原变形不是因式分解,故此选项不符合题意;
B、原变形是整式乘法,不是因式分解,故此选项不符合题意;
C、把一个多项式化为几个整式的积的形式,原变形是因式分解,故此选项符合题意;
D、左边不是多项式,原变形不是因式分解,故此选项不符合题意;
故选:C.
2.D
解:x-y= a2﹣6ab+9b2-(4a﹣12b﹣4)
a2﹣6ab+9b2-4a+12b+4
故选:D.
3.D
解:A、原式=9a6,不符合题意;
B、原式=2a3b-3a2+1,不符合题意;
C、原式=(4x6y4)×(-3x)=-12x7y4,不符合题意;
D、原式=(-27a9b6)×(b)=9a9b7,符合题意.
故选:D.
4.D
解:②型号卡片的面积为,③型号卡片的面积为,
∵,
∴需要②型号卡片2张,③型号卡片7张;
故答案选D.
5.A
解:∵a、b、c是三角形的边长,
∴,,
∴,,
∴,
故选A.
6.A
解:∵长方形的周长为16cm,它两邻边长分别为xcm,ycm,
∴,
∴①,
∵,
∴,
∴,
∴②,
联立①②解得,
∴长方形的面积,
故选A.
7.C
解:∵(3+x)(2x2+mx﹣5)=2x3+(6+m)x2+(﹣5+3m)x﹣15,
又∵结果中x2项的系数为﹣3,
∴6+m=﹣3,
解得m=﹣9.
故选:C.
8.B
解:∵,,
∴,故①错误;
∴,故②错误;
∴,故③正确,
故选B.
9.C
解:∵2a=3,2b=6,2c=12.
∴2a×22=3×4=12,2b×2=6×2=12,2c=12,
∴a+2=b+1=c,
即b=a+1,c=b+1,c=a+2,
于是有:①a+c=a+a+2=2a+2,2b=2a+2,
所以a+c=2b,因此①正确;
②a+b=a+a+1=2a+1,2c﹣3=2a+4﹣3=2a+1,
所以a+b=2c﹣3,因此②正确;
③b+c=a+1+a+2=2a+3,因此③正确;
④b=a+1,因此④不正确;
综上所述,正确的结论有:①②③三个,
故选:C.
10.D
解:
故答案为D
11.8a﹣6b+2
解:∵长方形的面积为4a2﹣6ab+2a,它的长为2a,
∴它的宽为:(4a2﹣6ab+2a)÷2a
=4a2÷2a﹣6ab÷2a+2a÷2a
=2a﹣3b+1,
∴它的周长为:2(2a﹣3b+1+2a)
=8a﹣6b+2.
故答案为:8a﹣6b+2.
12.4
解:∵,,
∴,
∵,,
∴,
联立得:,
解得:,
∴,
故答案为:4.
13.4
解:∵,,
∴
,
故答案为:4.
14.
解:∵
设①
②
①-②得,
故答案为:.
15.
解:∵和,
∴,,
∴,
将代入可得,
故答案为:-2.
16.30
解:设KF=a,FL=b,
由图可知EK=BH=LJ=GD=5-a,KH=EB=GL=DJ=5-b,
∴=2(5-a)(5-b)+ab=25-5a-5b+3ab,
=(5+5-b)(5+5-a)=100-10a-10b+ab,
∵,
∴3(100-10a-10b+ab)-(25-5a-5b+3ab)=150,
整理得a+b=5,
∴长方形ABCD的周长为2(AB+BC)=2(5+5-b+5+5-a)=30,
故答案为:30.
17.
解:原式=[(x-(2y-3))][x+(2y-3)]
=x2-(2y-3)2
=x2-4y2+12y-9
18.﹣1或7或-1
解:∵是一个完全平方式,
∴或,
即:或,
∴2(m﹣3)=±8,
解得:m=﹣1或m=7.
故答案为:﹣1或7.
19.3
解:∵a=2019x+2019,b=2019x+2020,c=2019x+2021,
∴a-b=-1,a-c=-2,b-c=-1,
∴
=
=
=
=3.
故答案为:3.
20.13
解:,,.
.
故答案为:13.
21.(1);(2)
解:(1)
展开式中不含x的二次项和一次项,
,
解得:,
;
(2)当时,
.
22.(1);(2)
解:(1)
.
(2)
.
23.(1);(2);(3);(4)
解:(1)
.
(2).
(3).
(4)
.
24.(1);(2);(3)
解:(1)继续小明的方法,12=42-22,13=72-62,15=82-72,16=52-32,
即第10个幸福数仿照小明的方法用等式表示出来:16=52-32.
故答案为:.
(2)假设是幸福数,则(m,n为正整数),
有,
.
若m,n奇偶性相同,则与均为偶数,
右边为4的倍数,而左边不是4的倍数,故不成立.
若m,n奇偶性不相同,则与均为奇数,
右边为奇数,而左边是2的倍数,是偶数,故不成立.
综上,不可能为两个正整数的平方差,
即不是幸福数.
(3)我们发现将正整数从小到大4个一组,第一组有1个幸福数,其余各组均有3个幸福数,
并且被4除余数是2的数都不是幸福数.
设第n个幸福数在第k组,则,,
即:,
,
又k为整数,.
第2021个幸福数在第675组.
前674组有幸福数(个),
第2021个幸福数是第675组的第1个数为.
.
25.(1),;(2);(3)①;②1
解:()方法1:阴影部分面积为4个相同的小长方形的面积之和,
∴阴影部分面积=;
方法2:阴影部分面积=大正方形的面积-小正方形面积
∴阴影部分面积=.
故答案为:,;
()∵(1)中两种方法求得的阴影部分面积相等,
∴;
()①∵,,,
∴,
∴;
②,,,
∴,
∴.
26.(1)a2+3ab+2b2;(2)(3a+b)(a+b)=3a2+4ab+b2;(3)画图解,2a2+3ab+b2;(4)5
解:(1)∵长方形的面积=a2+3ab+2b2,长方形的面积=(a+b)(a+2b),
∴(a+b)(a+2b)=a2+3ab+2b2,
故答案是:a2+3ab+2b2;
(2)∵长方形的面积=3a2+4ab+b2,长方形的面积=(3a+b)(a+b),
∴(3a+b)(a+b)=3a2+4ab+b2,
故答案是:(3a+b)(a+b)=3a2+4ab+b2;
(3)如图所示:
∴(2a+b)(a+b)=2a2+3ab+b2,
故答案是:2a2+3ab+b2;
(4)∵4a2+6ab+2b2=5,
∴2a2+3ab+b2=,
∵a+b=,(2a+b)(a+b)=2a2+3ab+b2,
∴2a+b=÷=5.
试卷第1页,共3页
单元综合优生辅导测试(附答案)
一、单选题(满分30分)
1.下列等式中,从左到右的变形是因式分解的是( )
A. B.
C. D.
2.已知a、b满足等式,x=a2﹣6ab+9b2.y=4a﹣12b﹣4,则x,y的大小关系是( )
A.x=y B.x>y C.x<y D.x≥y
3.下列计算正确的是( )
A. B.
C. D.
4.如图,现有足够多的型号为①②③的正方形和长方形卡片,如果分别选取这三种型号卡片若干张,可以拼成一个不重叠、无缝隙的长方形,小星想用拼图前后面积之间的关系.解释多项式乘法,则其中②和③型号卡片需要的张数各是( )
A.3张和7张 B.2张和3张 C.5张和7张 D.2张和7张
5.已知a、b、c是三角形的边长,那么代数式的值是( )
A.小于零 B.等于零 C.大于零 D.大小不确定
6.已知长方形的周长为16cm,它两邻边长分别为xcm,ycm,且满足,则该长方形的面积为( )cm2
A. B. C.15 D.16
7.若的计算结果中项的系数为,则为( )
A. B. C. D.
8.已知,,则计算①;②;③中错误的个数是( )
A.0 B.1 C.2 D.3
9.已知,,,现给出3个实数a,b,c之间的四个关系式:①;②;③;④.其中,正确的关系式的个数是( )
A.1 B.2 C.3 D.4
10.计算(1)(1)……(1)(1)的值是( )
A. B. C. D.
二、填空题(满分30分)
11.长方形的面积为,长为,则它的周长为______________.
12.已知,则_____.
13.已知,,则______.
14.将边长为1的正方形纸片按如图所示方法进行对折,记第1次对折后得到的图形面积为S1,第2次对折后得到的图形面积为S2,…,第n次对折后得到的图形面积为Sn,请根据图2化简, ______.
15.若,,则______.
16.如图所示,长方形ABCD中放置两个边长都为5的正方形AEFG与正方形CHIJ,若如图阴影部分的面积之和记为,长方形ABCD的面积记为,已知:,则长方形ABCD的周长为______.
17.计算:______.
18.若是一个完全平方式,则__________.
19.已知,,,则________.
20.如图,点M是AB中点,点P在MB上,分别以AP,BP为边作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=6,ab=7,则图中阴影部分的面积为______.
三、解答题(满分60分)
21.若(x﹣2)(x2+ax﹣8b)的展开式中不含x的二次项和一次项.
(1)求b的值;
(2)求(a+1)(a2+1)(a4+1)…(a32+1)+1的值.
22.分解因式:
(1);(2).
23.分解因式:
(1); (2);
(3); (4).
24.阅读理解题
问题提出:如果一个正整数能表示为两个正整数的平方差,那么称这个正整数为“幸福数”.例如,,16就是一个幸福数.我们按照从小到大的顺序把“3,5,7,8,…,,…” 这些幸福数进行排列依次记为:第1个幸福数3,第2个幸福数5,第3个幸福数7,第4个幸福数8,…,第个幸福数.现在需要探究出一种判断一个较大的数是否是幸福数的方法;以及如何求出第个幸福数的值.
实践探究:小明的方法是:在正整数中,从1开始采取从小到大逐个排查的办法一个一个找出来:
,,,
,,,
…
(1)请将第10个幸福数仿照小明的方法用等式表示出来: ;
小颖认为小明的方法太麻烦,她想到:设是正整数,由于,所以,除1外,所有的奇数都是幸福数;又因为所以,除4外,所有能被4整除的偶数都是幸福数;小颖通过上面的探索,已经证明了形如、、(是正整数)的正整数都是幸福数.
(2)请证明形如(是正整数)的数不是幸福数;
迁移应用:(3)当时,求的值.
25.数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图1可以解释完全平方公式:.
(1)如图2(图中各小长方形大小均相等),请用两种不同的方法求图2中阴影部分的面积(不化简):
方法1:_________________;
方法2∶_________________.
(2)由(1)中两种不同的方法,你能得到怎样的等式
(3)①已知,,请利用(2)中的等式,求的值.
②已知,,请利用(2)中的等式,求的值.
26.阅读下列文字:我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.图1给出了若干个边长为a和边长为b的小正方形纸片及若干个边长为c、b的长方形纸片.请解答下列问题:
(1)图2是由图1提供的几何图形拼接而得,可以得到(a+b)(a+2b)= ;
(2)请写出图3中所表示的数学等式: ;
(3)请按要求利用所给的纸片在图4的方框中拼出一个长方形,要求所拼出图形的面积为(2a+b)(a+b),进而可以得到等式:(2a+b)(a+b)= .
(4)利用(3)中得到的结论,解决下面的问题:若4a2+6ab+2b2=5,a+b=,求2a+b的值.
参考答案
1.C
解:A、不是把一个多项式化为几个整式的积的形式,原变形不是因式分解,故此选项不符合题意;
B、原变形是整式乘法,不是因式分解,故此选项不符合题意;
C、把一个多项式化为几个整式的积的形式,原变形是因式分解,故此选项符合题意;
D、左边不是多项式,原变形不是因式分解,故此选项不符合题意;
故选:C.
2.D
解:x-y= a2﹣6ab+9b2-(4a﹣12b﹣4)
a2﹣6ab+9b2-4a+12b+4
故选:D.
3.D
解:A、原式=9a6,不符合题意;
B、原式=2a3b-3a2+1,不符合题意;
C、原式=(4x6y4)×(-3x)=-12x7y4,不符合题意;
D、原式=(-27a9b6)×(b)=9a9b7,符合题意.
故选:D.
4.D
解:②型号卡片的面积为,③型号卡片的面积为,
∵,
∴需要②型号卡片2张,③型号卡片7张;
故答案选D.
5.A
解:∵a、b、c是三角形的边长,
∴,,
∴,,
∴,
故选A.
6.A
解:∵长方形的周长为16cm,它两邻边长分别为xcm,ycm,
∴,
∴①,
∵,
∴,
∴,
∴②,
联立①②解得,
∴长方形的面积,
故选A.
7.C
解:∵(3+x)(2x2+mx﹣5)=2x3+(6+m)x2+(﹣5+3m)x﹣15,
又∵结果中x2项的系数为﹣3,
∴6+m=﹣3,
解得m=﹣9.
故选:C.
8.B
解:∵,,
∴,故①错误;
∴,故②错误;
∴,故③正确,
故选B.
9.C
解:∵2a=3,2b=6,2c=12.
∴2a×22=3×4=12,2b×2=6×2=12,2c=12,
∴a+2=b+1=c,
即b=a+1,c=b+1,c=a+2,
于是有:①a+c=a+a+2=2a+2,2b=2a+2,
所以a+c=2b,因此①正确;
②a+b=a+a+1=2a+1,2c﹣3=2a+4﹣3=2a+1,
所以a+b=2c﹣3,因此②正确;
③b+c=a+1+a+2=2a+3,因此③正确;
④b=a+1,因此④不正确;
综上所述,正确的结论有:①②③三个,
故选:C.
10.D
解:
故答案为D
11.8a﹣6b+2
解:∵长方形的面积为4a2﹣6ab+2a,它的长为2a,
∴它的宽为:(4a2﹣6ab+2a)÷2a
=4a2÷2a﹣6ab÷2a+2a÷2a
=2a﹣3b+1,
∴它的周长为:2(2a﹣3b+1+2a)
=8a﹣6b+2.
故答案为:8a﹣6b+2.
12.4
解:∵,,
∴,
∵,,
∴,
联立得:,
解得:,
∴,
故答案为:4.
13.4
解:∵,,
∴
,
故答案为:4.
14.
解:∵
设①
②
①-②得,
故答案为:.
15.
解:∵和,
∴,,
∴,
将代入可得,
故答案为:-2.
16.30
解:设KF=a,FL=b,
由图可知EK=BH=LJ=GD=5-a,KH=EB=GL=DJ=5-b,
∴=2(5-a)(5-b)+ab=25-5a-5b+3ab,
=(5+5-b)(5+5-a)=100-10a-10b+ab,
∵,
∴3(100-10a-10b+ab)-(25-5a-5b+3ab)=150,
整理得a+b=5,
∴长方形ABCD的周长为2(AB+BC)=2(5+5-b+5+5-a)=30,
故答案为:30.
17.
解:原式=[(x-(2y-3))][x+(2y-3)]
=x2-(2y-3)2
=x2-4y2+12y-9
18.﹣1或7或-1
解:∵是一个完全平方式,
∴或,
即:或,
∴2(m﹣3)=±8,
解得:m=﹣1或m=7.
故答案为:﹣1或7.
19.3
解:∵a=2019x+2019,b=2019x+2020,c=2019x+2021,
∴a-b=-1,a-c=-2,b-c=-1,
∴
=
=
=
=3.
故答案为:3.
20.13
解:,,.
.
故答案为:13.
21.(1);(2)
解:(1)
展开式中不含x的二次项和一次项,
,
解得:,
;
(2)当时,
.
22.(1);(2)
解:(1)
.
(2)
.
23.(1);(2);(3);(4)
解:(1)
.
(2).
(3).
(4)
.
24.(1);(2);(3)
解:(1)继续小明的方法,12=42-22,13=72-62,15=82-72,16=52-32,
即第10个幸福数仿照小明的方法用等式表示出来:16=52-32.
故答案为:.
(2)假设是幸福数,则(m,n为正整数),
有,
.
若m,n奇偶性相同,则与均为偶数,
右边为4的倍数,而左边不是4的倍数,故不成立.
若m,n奇偶性不相同,则与均为奇数,
右边为奇数,而左边是2的倍数,是偶数,故不成立.
综上,不可能为两个正整数的平方差,
即不是幸福数.
(3)我们发现将正整数从小到大4个一组,第一组有1个幸福数,其余各组均有3个幸福数,
并且被4除余数是2的数都不是幸福数.
设第n个幸福数在第k组,则,,
即:,
,
又k为整数,.
第2021个幸福数在第675组.
前674组有幸福数(个),
第2021个幸福数是第675组的第1个数为.
.
25.(1),;(2);(3)①;②1
解:()方法1:阴影部分面积为4个相同的小长方形的面积之和,
∴阴影部分面积=;
方法2:阴影部分面积=大正方形的面积-小正方形面积
∴阴影部分面积=.
故答案为:,;
()∵(1)中两种方法求得的阴影部分面积相等,
∴;
()①∵,,,
∴,
∴;
②,,,
∴,
∴.
26.(1)a2+3ab+2b2;(2)(3a+b)(a+b)=3a2+4ab+b2;(3)画图解,2a2+3ab+b2;(4)5
解:(1)∵长方形的面积=a2+3ab+2b2,长方形的面积=(a+b)(a+2b),
∴(a+b)(a+2b)=a2+3ab+2b2,
故答案是:a2+3ab+2b2;
(2)∵长方形的面积=3a2+4ab+b2,长方形的面积=(3a+b)(a+b),
∴(3a+b)(a+b)=3a2+4ab+b2,
故答案是:(3a+b)(a+b)=3a2+4ab+b2;
(3)如图所示:
∴(2a+b)(a+b)=2a2+3ab+b2,
故答案是:2a2+3ab+b2;
(4)∵4a2+6ab+2b2=5,
∴2a2+3ab+b2=,
∵a+b=,(2a+b)(a+b)=2a2+3ab+b2,
∴2a+b=÷=5.
试卷第1页,共3页
