第一章 1.2 1.2.1 测量距离或高度问题
文档属性
| 名称 | 第一章 1.2 1.2.1 测量距离或高度问题 |  | |
| 格式 | zip | ||
| 文件大小 | 439.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 09:52:35 | ||
图片预览




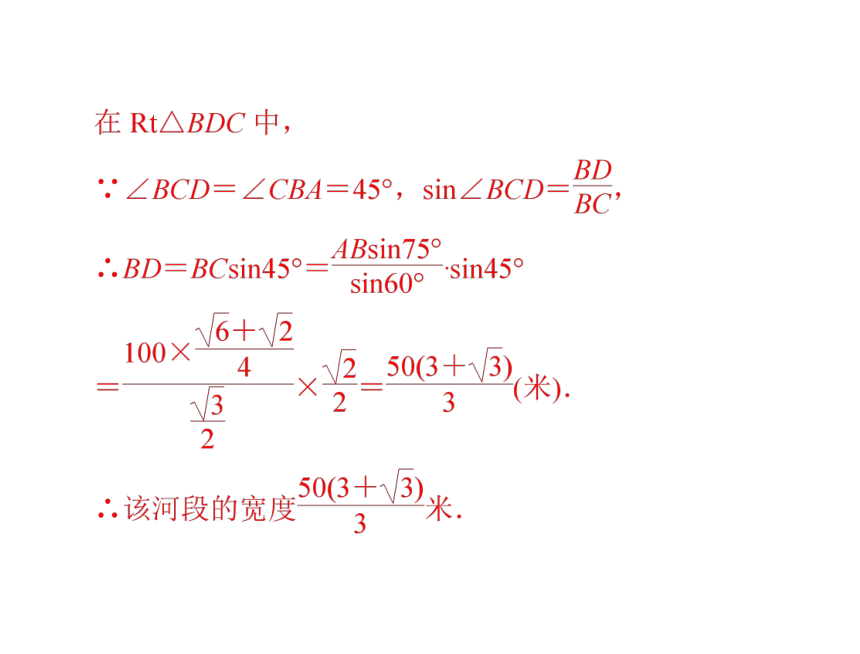


文档简介
(共24张PPT)
1.2
应用举例
1.2.1 测量距离或高度问题
1.能正确运用正弦定理和余弦定理等知识和方法解决一些
有关测量不能到达的一点或两点的距离的实际问题.
2.能正确运用正弦定理和余弦定理等知识和方法解决一些
有关底部不可到达的物体高度测量问题.
3.巩固深化解三角形实际问题的一般方法,养成良好的研
究、探索习惯.
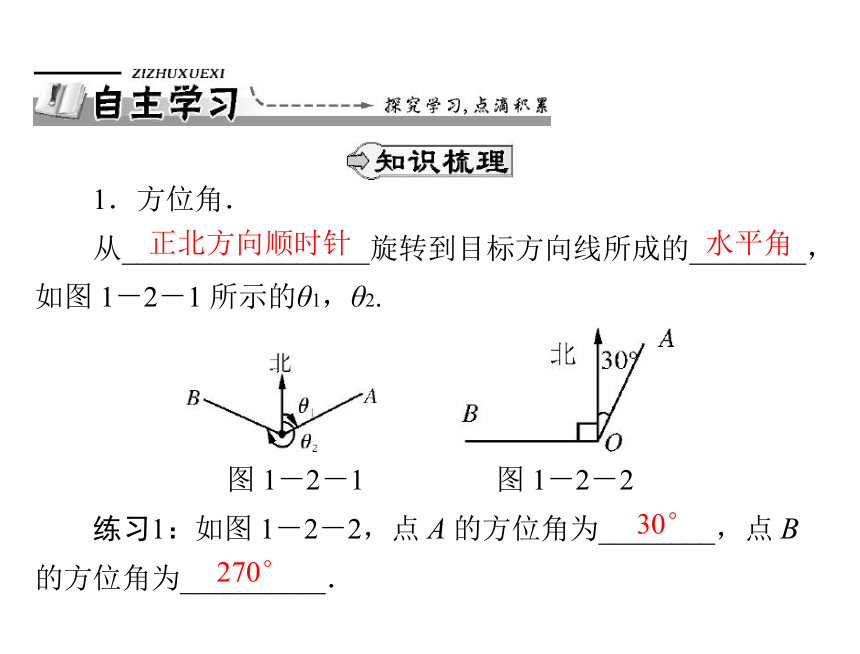
1.方位角.
正北方向顺时针
水平角
从_________________旋转到目标方向线所成的________,
如图 1-2-1 所示的θ1,θ2.
图 1-2-1
图 1-2-2
练习1:如图 1-2-2,点 A 的方位角为________,点 B
的方位角为__________.
30°
270°
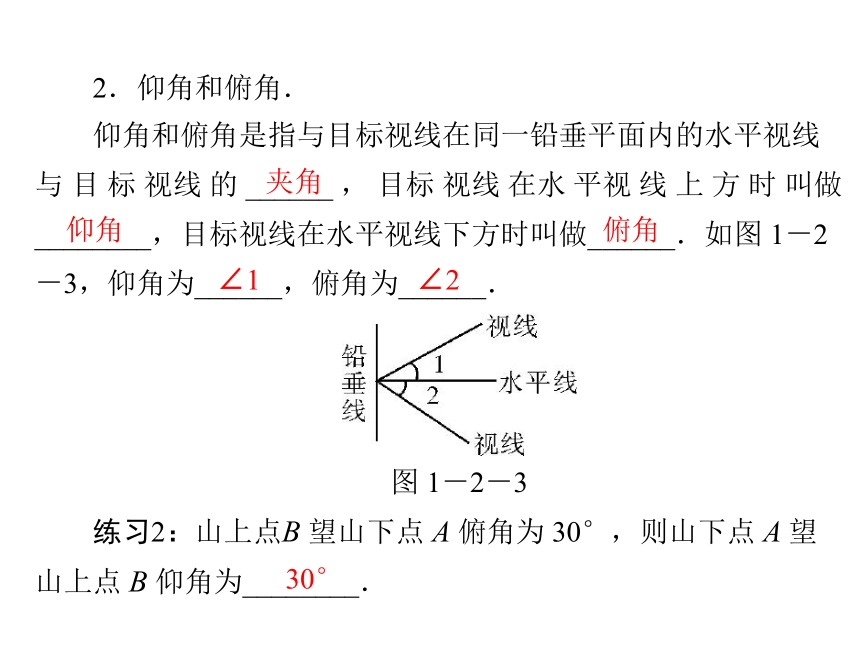
2.仰角和俯角.
夹角
仰角
俯角
∠1
∠2
仰角和俯角是指与目标视线在同一铅垂平面内的水平视线
与 目 标 视线 的 ______ , 目标 视线 在水 平视 线 上 方 时 叫做
________,目标视线在水平视线下方时叫做______.如图 1-2
-3,仰角为______,俯角为______.
图 1-2-3
练习2:山上点B 望山下点 A 俯角为 30°,则山下点 A 望
山上点 B 仰角为________.
30°
1.测量一已知目标与另一无法到达的目标距离时,利用正
弦定理求解需要哪些条件?
答案:选取一个目标,并给目标与可到达目标的距离,再
分别测量该两点与不可到达目标的夹角.
2.测量某一物体高度时,利用余弦定理求解需要哪些条
件?
答案:选取地面两点与物体底部在同一直线上,测量选取
的两点的距离,再分别测量该两点与物体顶点的夹角.
题型1
测量宽度
例1:如图 1-2-4 某河段的两岸可视为平行,为了测量
该河段的宽度,在河段的一岸边选取两点 A,B,观察对岸的点
C,测得∠CAB=75°,∠CBA=45°,且 AB=100 米.
(1)求 sin75°;
(2)求该河段的宽度.
图 1-2-4
过点 B 作 BD 垂直于 CD,垂足为点 D,则 BD 的长就是该
河段的宽度.
【变式与拓展】
1.为了在一条河上建一座桥,施工前在河两岸打上两个桥
位桩 A,B(如图 1-2-5),要测算 A,B 两点的距离,测量人员
在岸边定出基线 BC,测得 BC=50 m,∠ABC=105°,∠BCA
)
A
=45°,就可以计算出 A,B 两点的距离为(
图 1-2-5
2.如图 1-2-6,为了测定河的宽度,在一岸边选定两点
A,B,对岸标记物 C,测得∠CAB=30°,∠CBA=75°,AB
60 m
= 120 m,则河的宽度为_________.
图 1-2-6
题型2
求不可到达两点之间的距离问题
例2:如图 1-2-7,A,B 两点都在河的对岸(不可到达),
在河岸边选定两点 C,D,测得 CD=1 000 米,∠ACB=30°,
∠BCD=30°,∠BDA=30°,∠ADC=60°,求 AB 的长.
图 1-2-7
测量不能达到的两点间的距离,利用解斜三角
形是一个重要的方法.解决这类问题的关键是构造一个或几个
三角形,测出有关边长和角,用正、余弦定理进行计算.
【变式与拓展】
3.某炮兵阵地位于地面 A 处,两观察所分别位于地面点 C
和点 D 处,已知 CD=6 km,∠ACD=45°,∠ADC=75°,目
标出现于地面点 B处时,测得∠BCD=30°,∠BDC=15°,如
图 1-2-8,则炮兵阵地到目的的距离为__________.
图 1-2-8
4.如图 1-2-9,现要计算北江岸边两景点 B 与 C 的距离.
由于地形的限制,需要在岸上选取 A 和 D 两个测量点,现测得
AD⊥CD,AD=10 km,AB=14 km,∠BDA=60°,∠BCD=
135°,求两景点B与C的距离.(假设A,B,C,D 在同一平面
内,测量结果保留整数;参考数据: ≈1.414)
图 1-2-9
题型3
测量高度问题
例3:河对岸有一个建筑物,建筑物的底部不可到达,请
你利用量角器和米尺设计出一套方案测出建筑物的高度.
,
AC=AB·
1
tanα
图 D1
自主解答:方法一:如图 D1,在河的一边取两点 C,D,
使 C,D 与建筑物底部的中心在同一直线上.测得 CD=a,
∠BCA=α,∠BDA=β.设AB=x,则AC与AD都能用 x 表示,
由AD-AC=a,可求得 x.
设 AB=x,则在 Rt△BAC 中,
图D2
解决这类设计测量方案问题时,应先进行发散
思维——联想数学模型,寻求解决问题的各种方案,然后进行
收敛思维——比较各种方案的优劣,考虑计算量的大小,是否
具备可操作性以及实施测量的工作量的大小等等.
【变式与拓展】
5.在某个位置测得某山峰仰角为θ,对着山峰在平行地面
上前进 600 m 后测仰角为原来的 2 倍,继续在平行地面上前进
200
是(
m 后,测得山峰的仰角为原来的 4 倍,则该山峰的高度
)
B
A.200 m
C.400 m
B.300 m
D.100 m
6.如图 1-2-10,为了测量某塔的高度,某人站在 A 处
测得塔尖的仰角为 60°,前进 38.5 m 后,达到 B 处测得塔尖的
图 1-2-10
仰角为 75°.试计算该塔的高度(精确到 1 m).
,
∴BC=
在△ABC 中,∵
AB
sin∠ACB
=
BC
sinA
AB·sinA
sin∠ACB
=
38.5·sin60°
sin15°
.
∴CD=BC·sin75°=
38.5·sin60°
sin15°
·sin75°≈91(m).
解:∵∠CAD=60°,∠CBD=75°,
∴∠ACB=15°.
例4:在 200 米高的山顶上,测得山下一塔顶与塔底的俯
角分别为 30°,60°,求该塔的高度.
图 D3
试解:如图 D3.
B 为山顶,AB=200 米,CD 为塔高,
EB 为水平线,DC 延长线交 BE 于点 E,
∠EBC=30°,∠EBD=60°.
在 Rt△BDE 中,DE=AB=200,
BE=DE·tan30°=
200
3
,
在 Rt△BCE 中,EC=BE·tan30°=
=
200
3
,
∴CD=DE-CE=200-
200 400
3 3
(米).
易错点评:题意理解不清,不能正确画出图形.
1.解决实际测量问题一般要充分认真理解题意,正确作出
图形,从中抽象出一个或几个三角形,把实际问题里的条件和
所求转换成三角形的已知和未知的边、角,然后解三角形,得
到实际问题的解.
2.测量高度的一般方法是选择能观察到测量物体的两点,
分别测量仰角或俯角,同时测量出两个观测点的距离,再利用
解三角形的方法来计算.
3.解斜三角形应用题的一般步骤.
(1)分析:理解题意,分清已知与未知,画出示意图;
(2)建模:根据已知条件与求解目标,把已知量与求解量尽
量集中在有关的三角形中,建立一个解斜三角形的数学模型;
(3)求解:利用正弦定理或余弦定理有序地解三角形,求得
数学模型的解;
(4)检验:检验上述所求的解是否符合实际意义,从而得出
实际问题的解.
1.2
应用举例
1.2.1 测量距离或高度问题
1.能正确运用正弦定理和余弦定理等知识和方法解决一些
有关测量不能到达的一点或两点的距离的实际问题.
2.能正确运用正弦定理和余弦定理等知识和方法解决一些
有关底部不可到达的物体高度测量问题.
3.巩固深化解三角形实际问题的一般方法,养成良好的研
究、探索习惯.
1.方位角.
正北方向顺时针
水平角
从_________________旋转到目标方向线所成的________,
如图 1-2-1 所示的θ1,θ2.
图 1-2-1
图 1-2-2
练习1:如图 1-2-2,点 A 的方位角为________,点 B
的方位角为__________.
30°
270°
2.仰角和俯角.
夹角
仰角
俯角
∠1
∠2
仰角和俯角是指与目标视线在同一铅垂平面内的水平视线
与 目 标 视线 的 ______ , 目标 视线 在水 平视 线 上 方 时 叫做
________,目标视线在水平视线下方时叫做______.如图 1-2
-3,仰角为______,俯角为______.
图 1-2-3
练习2:山上点B 望山下点 A 俯角为 30°,则山下点 A 望
山上点 B 仰角为________.
30°
1.测量一已知目标与另一无法到达的目标距离时,利用正
弦定理求解需要哪些条件?
答案:选取一个目标,并给目标与可到达目标的距离,再
分别测量该两点与不可到达目标的夹角.
2.测量某一物体高度时,利用余弦定理求解需要哪些条
件?
答案:选取地面两点与物体底部在同一直线上,测量选取
的两点的距离,再分别测量该两点与物体顶点的夹角.
题型1
测量宽度
例1:如图 1-2-4 某河段的两岸可视为平行,为了测量
该河段的宽度,在河段的一岸边选取两点 A,B,观察对岸的点
C,测得∠CAB=75°,∠CBA=45°,且 AB=100 米.
(1)求 sin75°;
(2)求该河段的宽度.
图 1-2-4
过点 B 作 BD 垂直于 CD,垂足为点 D,则 BD 的长就是该
河段的宽度.
【变式与拓展】
1.为了在一条河上建一座桥,施工前在河两岸打上两个桥
位桩 A,B(如图 1-2-5),要测算 A,B 两点的距离,测量人员
在岸边定出基线 BC,测得 BC=50 m,∠ABC=105°,∠BCA
)
A
=45°,就可以计算出 A,B 两点的距离为(
图 1-2-5
2.如图 1-2-6,为了测定河的宽度,在一岸边选定两点
A,B,对岸标记物 C,测得∠CAB=30°,∠CBA=75°,AB
60 m
= 120 m,则河的宽度为_________.
图 1-2-6
题型2
求不可到达两点之间的距离问题
例2:如图 1-2-7,A,B 两点都在河的对岸(不可到达),
在河岸边选定两点 C,D,测得 CD=1 000 米,∠ACB=30°,
∠BCD=30°,∠BDA=30°,∠ADC=60°,求 AB 的长.
图 1-2-7
测量不能达到的两点间的距离,利用解斜三角
形是一个重要的方法.解决这类问题的关键是构造一个或几个
三角形,测出有关边长和角,用正、余弦定理进行计算.
【变式与拓展】
3.某炮兵阵地位于地面 A 处,两观察所分别位于地面点 C
和点 D 处,已知 CD=6 km,∠ACD=45°,∠ADC=75°,目
标出现于地面点 B处时,测得∠BCD=30°,∠BDC=15°,如
图 1-2-8,则炮兵阵地到目的的距离为__________.
图 1-2-8
4.如图 1-2-9,现要计算北江岸边两景点 B 与 C 的距离.
由于地形的限制,需要在岸上选取 A 和 D 两个测量点,现测得
AD⊥CD,AD=10 km,AB=14 km,∠BDA=60°,∠BCD=
135°,求两景点B与C的距离.(假设A,B,C,D 在同一平面
内,测量结果保留整数;参考数据: ≈1.414)
图 1-2-9
题型3
测量高度问题
例3:河对岸有一个建筑物,建筑物的底部不可到达,请
你利用量角器和米尺设计出一套方案测出建筑物的高度.
,
AC=AB·
1
tanα
图 D1
自主解答:方法一:如图 D1,在河的一边取两点 C,D,
使 C,D 与建筑物底部的中心在同一直线上.测得 CD=a,
∠BCA=α,∠BDA=β.设AB=x,则AC与AD都能用 x 表示,
由AD-AC=a,可求得 x.
设 AB=x,则在 Rt△BAC 中,
图D2
解决这类设计测量方案问题时,应先进行发散
思维——联想数学模型,寻求解决问题的各种方案,然后进行
收敛思维——比较各种方案的优劣,考虑计算量的大小,是否
具备可操作性以及实施测量的工作量的大小等等.
【变式与拓展】
5.在某个位置测得某山峰仰角为θ,对着山峰在平行地面
上前进 600 m 后测仰角为原来的 2 倍,继续在平行地面上前进
200
是(
m 后,测得山峰的仰角为原来的 4 倍,则该山峰的高度
)
B
A.200 m
C.400 m
B.300 m
D.100 m
6.如图 1-2-10,为了测量某塔的高度,某人站在 A 处
测得塔尖的仰角为 60°,前进 38.5 m 后,达到 B 处测得塔尖的
图 1-2-10
仰角为 75°.试计算该塔的高度(精确到 1 m).
,
∴BC=
在△ABC 中,∵
AB
sin∠ACB
=
BC
sinA
AB·sinA
sin∠ACB
=
38.5·sin60°
sin15°
.
∴CD=BC·sin75°=
38.5·sin60°
sin15°
·sin75°≈91(m).
解:∵∠CAD=60°,∠CBD=75°,
∴∠ACB=15°.
例4:在 200 米高的山顶上,测得山下一塔顶与塔底的俯
角分别为 30°,60°,求该塔的高度.
图 D3
试解:如图 D3.
B 为山顶,AB=200 米,CD 为塔高,
EB 为水平线,DC 延长线交 BE 于点 E,
∠EBC=30°,∠EBD=60°.
在 Rt△BDE 中,DE=AB=200,
BE=DE·tan30°=
200
3
,
在 Rt△BCE 中,EC=BE·tan30°=
=
200
3
,
∴CD=DE-CE=200-
200 400
3 3
(米).
易错点评:题意理解不清,不能正确画出图形.
1.解决实际测量问题一般要充分认真理解题意,正确作出
图形,从中抽象出一个或几个三角形,把实际问题里的条件和
所求转换成三角形的已知和未知的边、角,然后解三角形,得
到实际问题的解.
2.测量高度的一般方法是选择能观察到测量物体的两点,
分别测量仰角或俯角,同时测量出两个观测点的距离,再利用
解三角形的方法来计算.
3.解斜三角形应用题的一般步骤.
(1)分析:理解题意,分清已知与未知,画出示意图;
(2)建模:根据已知条件与求解目标,把已知量与求解量尽
量集中在有关的三角形中,建立一个解斜三角形的数学模型;
(3)求解:利用正弦定理或余弦定理有序地解三角形,求得
数学模型的解;
(4)检验:检验上述所求的解是否符合实际意义,从而得出
实际问题的解.
