第一章 1.2 1.2.2 测量角度问题
文档属性
| 名称 | 第一章 1.2 1.2.2 测量角度问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 350.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 00:00:00 | ||
图片预览







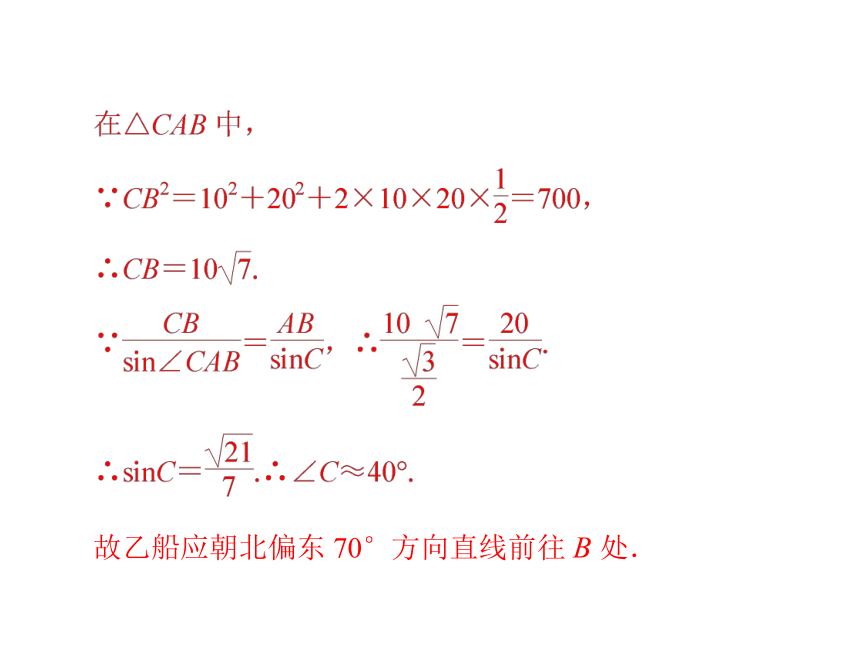
文档简介
(共21张PPT)
1.2.2 测量角度问题
能够运用正弦定理、余弦定理等知识和方法解决一些有关
计算角度的实际问题.
1.复习仰角、俯角、方位角与方向角的含义(见前面章节).
2.坡角是指斜坡所在平面与________的夹角.坡度(坡比)
是指___________________________________________.
练习:沿坡角为 45°的斜坡直线向上行走 80 m,实际升高
了________m.
水平面
坡面的垂直高度 h 和水平宽度 l 的比
40
解析:h=80×sin45°=40 .
1.仰角、俯角、坡角都是锐角吗?
答案:是.
2.方位角与方向角的范围一样吗?
答案:不一样,方位角的取值范围为0°~360°,方向角一
般指锐角.
题型1
船的航向问题
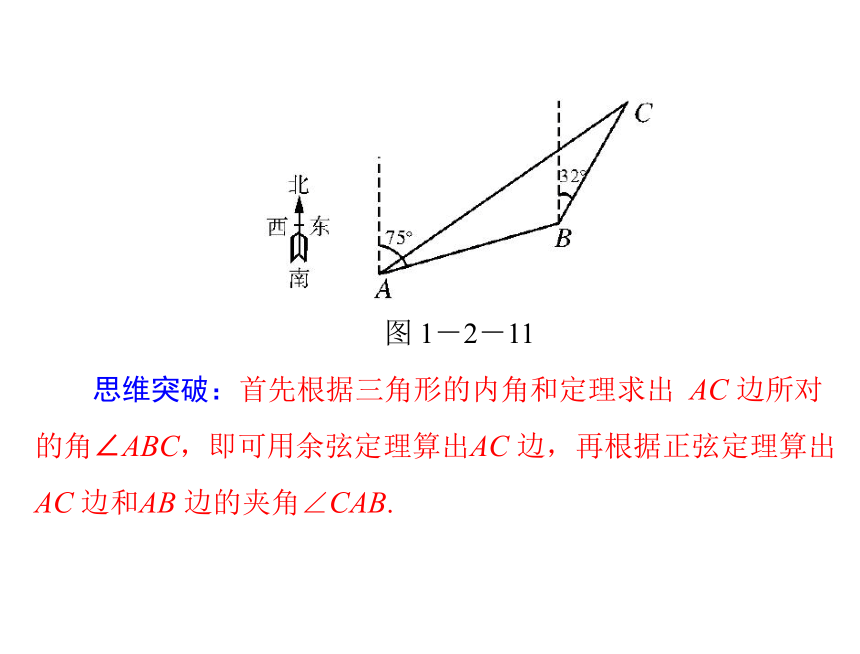
例1:如图 1-2-11,一艘海轮从 A 出发,沿北偏东 75°
的方向航行 67.5 n mile 后到达海岛 B,然后从 B 出发,沿北偏
东 32°的方向航行 54.0 n mile 后达到海岛 C.如果下次航行直接
从 A 出发到达 C,此船应该沿怎样的方向航行,需要航行多少
距离(角度精确到 0.1°,距离精确到 0.01 n mile)
图 1-2-11
思维突破:首先根据三角形的内角和定理求出 AC 边所对
的角∠ABC,即可用余弦定理算出AC 边,再根据正弦定理算出
AC 边和AB 边的夹角∠CAB.
解三角形问题中,求某些角的度数时,最好用
余弦定理求角.因为余弦函数在(0,π)上是单调递减的,而正
弦函数在(0,π)上不是一一对应,一个正弦值可以对应两个角.
但角在
上时,用正、余弦定理皆可.
【变式与拓展】
1.当甲船位于 A 处时获悉在其正东方向相距 20 海里的 B
处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息
告知在甲船的南偏西 30°,相距 10 海里 C 处的乙船,试问乙船
应朝北偏东多少度的方向沿直线前往 B 处救援(角度精确到 1°)
∠CAB=120°.
图 D5
解:如图 D5,要求乙船的航向,
即求∠ACB 的度数.
易知 C<90°,AB=20,AC=10,
故乙船应朝北偏东 70°方向直线前往 B 处.
题型2
解三角形与函数的综合
例2:在某海滨城市附近海面有一台风,据监测,当前台
) 方向
风中心位于城市O(如图1 -2 -12)的东偏南θ(cosθ=
300 km 的海面 P 处,并以 20 km/h 的
速度向西偏北 45°方向移动,台风侵袭
的范围为圆形区域,当前半径为 60 km,
并以 10 km/h 的速度不断增大,问几小
时后该城市开始受到台风的侵袭?受到
台风的侵袭的时间有多少小时?
图 1-2-12
答:12 小时后该城市开始受到台风侵袭,受到台风的侵袭
的时间有 12 小时.
【变式与拓展】
2.如图 1-2-13,甲船在 A 处发现乙船在北偏东 45°与 A
的距离为 10 海里的 C 处,正以 20 海里/小时的速度向南偏东
75°的方向航行,已知甲船的速度是20
海里/小时.问:甲船
沿什么方向,用多少时间才能与乙船相遇?
图 1-2-13
解:设 t 小时后相遇,则 BC,AB 的长分别为 20t 海里、
20 t 海里.
由图可知:∠ACB=120°.
由余弦定理,得
AB2=AC2+BC2-2AC·BC·cos∠ACB,
∴∠BAC=30°.∴甲船应沿北偏东 75°方向航行.
答:甲船应沿北偏东 75°方向航行半小时后才能与乙船相
遇.
例3:某观测站 C 在 A 城的南偏西 20°的方向,由 A 城出
发的一条公路,走向是南偏东 40°,由 C 处测得距 C 为 31 km
的公路上 B 处,有一人正沿公路向 A 城走去,走了 20 km 后到
达 D 处,此时 CD 的间距为 21 km,问:这个人还走多少千米
到达 A 城?
试解:在△ACD 中,已知 CD=21 km,∠CAD=60°,
只需再求出一个量即可.
如图 D4,设∠ACD=α,∠CDB=β.
在△CBD 中,由余弦定理,得
图 D4
易错点评:本题在解△ACD 时,利用余弦定理求AD,会
得出两个根,产生了增根,应对其进行验证,若应用正弦定理
来求解可避免这种情况.
∴这个人再走 15 km 就可到达 A 城.
1.测量角度问题是指无法直接用量角器测量角度的求解问
题.在实际生活中,要测量角的大小,求三角形中角度的大小,
求不能直接测得的角,求轮船航行时航速与航向等问题均可结
合正弦定理及余弦定理,通过解三角形求解.在解决与测量问
题有关的题目时,要搞清楚仰角、俯角、方位角与方向角的含
义,合理的构造三角形求解,即把实际问题数学化.
2.解三角形的应用题时,通常会遇到两种情况,如下:
(1)已知量与未知量全部集中在一个三角形中,依次利用正
弦定理或余弦定理解之.
(2)已知量与未知量涉及两个或几个三角形,这时需要选择
条件足够的三角形优先研究,再逐步在其余的三角形中求出问
题的解.
1.2.2 测量角度问题
能够运用正弦定理、余弦定理等知识和方法解决一些有关
计算角度的实际问题.
1.复习仰角、俯角、方位角与方向角的含义(见前面章节).
2.坡角是指斜坡所在平面与________的夹角.坡度(坡比)
是指___________________________________________.
练习:沿坡角为 45°的斜坡直线向上行走 80 m,实际升高
了________m.
水平面
坡面的垂直高度 h 和水平宽度 l 的比
40
解析:h=80×sin45°=40 .
1.仰角、俯角、坡角都是锐角吗?
答案:是.
2.方位角与方向角的范围一样吗?
答案:不一样,方位角的取值范围为0°~360°,方向角一
般指锐角.
题型1
船的航向问题
例1:如图 1-2-11,一艘海轮从 A 出发,沿北偏东 75°
的方向航行 67.5 n mile 后到达海岛 B,然后从 B 出发,沿北偏
东 32°的方向航行 54.0 n mile 后达到海岛 C.如果下次航行直接
从 A 出发到达 C,此船应该沿怎样的方向航行,需要航行多少
距离(角度精确到 0.1°,距离精确到 0.01 n mile)
图 1-2-11
思维突破:首先根据三角形的内角和定理求出 AC 边所对
的角∠ABC,即可用余弦定理算出AC 边,再根据正弦定理算出
AC 边和AB 边的夹角∠CAB.
解三角形问题中,求某些角的度数时,最好用
余弦定理求角.因为余弦函数在(0,π)上是单调递减的,而正
弦函数在(0,π)上不是一一对应,一个正弦值可以对应两个角.
但角在
上时,用正、余弦定理皆可.
【变式与拓展】
1.当甲船位于 A 处时获悉在其正东方向相距 20 海里的 B
处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息
告知在甲船的南偏西 30°,相距 10 海里 C 处的乙船,试问乙船
应朝北偏东多少度的方向沿直线前往 B 处救援(角度精确到 1°)
∠CAB=120°.
图 D5
解:如图 D5,要求乙船的航向,
即求∠ACB 的度数.
易知 C<90°,AB=20,AC=10,
故乙船应朝北偏东 70°方向直线前往 B 处.
题型2
解三角形与函数的综合
例2:在某海滨城市附近海面有一台风,据监测,当前台
) 方向
风中心位于城市O(如图1 -2 -12)的东偏南θ(cosθ=
300 km 的海面 P 处,并以 20 km/h 的
速度向西偏北 45°方向移动,台风侵袭
的范围为圆形区域,当前半径为 60 km,
并以 10 km/h 的速度不断增大,问几小
时后该城市开始受到台风的侵袭?受到
台风的侵袭的时间有多少小时?
图 1-2-12
答:12 小时后该城市开始受到台风侵袭,受到台风的侵袭
的时间有 12 小时.
【变式与拓展】
2.如图 1-2-13,甲船在 A 处发现乙船在北偏东 45°与 A
的距离为 10 海里的 C 处,正以 20 海里/小时的速度向南偏东
75°的方向航行,已知甲船的速度是20
海里/小时.问:甲船
沿什么方向,用多少时间才能与乙船相遇?
图 1-2-13
解:设 t 小时后相遇,则 BC,AB 的长分别为 20t 海里、
20 t 海里.
由图可知:∠ACB=120°.
由余弦定理,得
AB2=AC2+BC2-2AC·BC·cos∠ACB,
∴∠BAC=30°.∴甲船应沿北偏东 75°方向航行.
答:甲船应沿北偏东 75°方向航行半小时后才能与乙船相
遇.
例3:某观测站 C 在 A 城的南偏西 20°的方向,由 A 城出
发的一条公路,走向是南偏东 40°,由 C 处测得距 C 为 31 km
的公路上 B 处,有一人正沿公路向 A 城走去,走了 20 km 后到
达 D 处,此时 CD 的间距为 21 km,问:这个人还走多少千米
到达 A 城?
试解:在△ACD 中,已知 CD=21 km,∠CAD=60°,
只需再求出一个量即可.
如图 D4,设∠ACD=α,∠CDB=β.
在△CBD 中,由余弦定理,得
图 D4
易错点评:本题在解△ACD 时,利用余弦定理求AD,会
得出两个根,产生了增根,应对其进行验证,若应用正弦定理
来求解可避免这种情况.
∴这个人再走 15 km 就可到达 A 城.
1.测量角度问题是指无法直接用量角器测量角度的求解问
题.在实际生活中,要测量角的大小,求三角形中角度的大小,
求不能直接测得的角,求轮船航行时航速与航向等问题均可结
合正弦定理及余弦定理,通过解三角形求解.在解决与测量问
题有关的题目时,要搞清楚仰角、俯角、方位角与方向角的含
义,合理的构造三角形求解,即把实际问题数学化.
2.解三角形的应用题时,通常会遇到两种情况,如下:
(1)已知量与未知量全部集中在一个三角形中,依次利用正
弦定理或余弦定理解之.
(2)已知量与未知量涉及两个或几个三角形,这时需要选择
条件足够的三角形优先研究,再逐步在其余的三角形中求出问
题的解.
