《生活中的比》(教案)北师大版数学六年级上册
文档属性
| 名称 | 《生活中的比》(教案)北师大版数学六年级上册 |  | |
| 格式 | zip | ||
| 文件大小 | 572.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 11:34:51 | ||
图片预览



文档简介
《生活中的比》教学设计
教学内容:
义务教育课程标准实验教科书(北师大版)小学数学第十一册P48——50。
教材分析
《生活中的比》是在学生已经学过除法的意义、分数的意义以及分数与除法的关系的基础上学习的,是《比的认识》这一单元的起始课。比在数学中是一个重要的概念,体会比的意义和价值是教材内容的数学核心思想。教材以系列情境为学生理解比的意义提供了丰富的直观背景和具体案例。但要用足用好这些情境,真正达到帮助学生理解比的本质的目的,需要创造性地使用教材。因此,本课的教学设计在教学内容的处理方面有以下几点思考:
1、创设问题情境,帮助学生在具体的情境中抽象出比的意义,初步体会学习比的必要性、为引出比的意义做好铺垫。
2、根据历史资料引出比的意义,再以生活为主线,让学生在生活实例中体验比与除法的关系
教学目标
知识目标:经历从具体情境中抽象出比的过程,理解比的意义、能正确读写比、认识比各部份的名称。
能力目标:能利用比的知识解释一些简单的生活问题。
情感目标:感受比在生活中的广泛存在。
教学重点
理解比的意义。
教学难点
理解比的意义。
教学过程
一、创设情境,在情境中体会引入比的必要性,初步感知比的意义。
1、出示情境1。
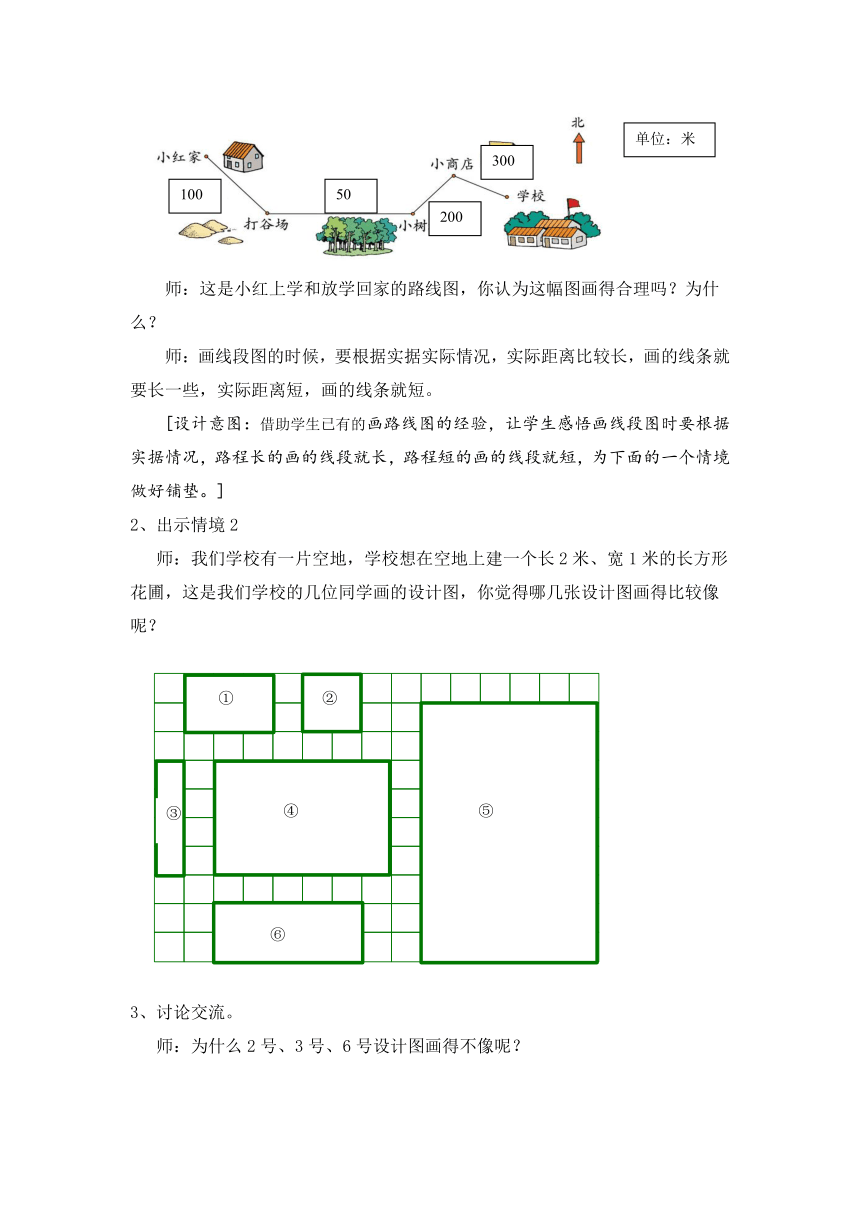
师:这是小红上学和放学回家的路线图,你认为这幅图画得合理吗?为什么?
师:画线段图的时候,要根据实据实际情况,实际距离比较长,画的线条就要长一些,实际距离短,画的线条就短。
[设计意图:借助学生已有的画路线图的经验,让学生感悟画线段图时要根据实据情况,路程长的画的线段就长,路程短的画的线段就短,为下面的一个情境做好铺垫。]
2、出示情境2
师:我们学校有一片空地,学校想在空地上建一个长2米、宽1米的长方形花圃,这是我们学校的几位同学画的设计图,你觉得哪几张设计图画得比较像呢?
3、讨论交流。
师:为什么2号、3号、6号设计图画得不像呢?
为什么这1号、4号、5号设计图会比较像呢?究竟蕴藏差怎样的秘密呢?
观察这几个长方形,在小组里说一说你发现了什么?
学生小组交流
全班交流
可能出现的答案:
这几个长方形的长都是宽的1.5倍。
这几个长方形的宽是长的三分之二。
……
4、还可以怎么画。
师:如果让同学们也来画这个花圃的设计图,还可以怎么画呢?
学生汇报。
师:画得完吗?(……)
师:观察这组数据,什么在变,什么没变?
(长与宽的厘米数在变,长与宽之间的倍数关系没变)
师:那么这些长方形的长与宽之间存在着怎样的关系呢?
学生个别回答。
师:这可以用一种新的表示方法——比。我们可以说这些长方形长与宽的比是(3)比( 2)。
花圃的长3米,宽2米,我们在画花圃的设计图时只要按长与宽的比是3比2来画就会画得像,其实设计师画在画设计图时也要应用到这个知识。
揭示课题——生活中的比
[设计意图:这一环节通过数形结合,让学生辨别哪张设计图画得好,引导学生探索长方形的长与宽之间的关系,发现1号、4号、5号长方形的长与宽存在着固定的倍数关系,再让学生接着画花圃的设计图,学生通过画设计图,体会到长方形的长与宽的厘米数在变,但长与宽之间的倍数关系没有变,怎样用一句话来总结这些长方形共同的特点呢?出此引出比,使学生对“比”有初步的体验,同时,让学生体会到引入比的必要性。]
二、引用历史资料,揭示比的意义,自学比的读写、比各部份的名称。
1、揭示比的意义。
师:比与我们学过的哪些知识有关联呢?让我们一起来看看著名数学家莱布尼兹是怎么说的。
课件出示——你知道吗?
十七世纪,著名数学家莱布尼兹认为,因为两个数相除又叫做两个数的比,所以比号与除号有一种亲缘关系。而比号与除号又不能共用,所以就把 “÷ ” 中的小横线去掉,于是“∶”就成为了比号。
师:现在你知道什么叫做比吗
板书:两个数相除,又叫做这两个数的比。
师:从这段话中你还知道了什么?(比号的写法)
如果用a÷b表示“两个数相除”, a比b该怎么写呢?
师:a、b可以是任意一个数吗?为什么?
板书:b≠0
2、学生带着问题自学课本。
师:现在请同学们打开课本,翻到第50页,划出比的定义。
师:再请同学们带着这两个问题自学课本。
3、全班交流。
师:通过自学,你还知道了什么?
课件出示:
6÷4写作 6:4 读作 6比4
师强调:比号前面的数叫做比的前项,比号后面的数叫做比的后项。用比的前项除以比的后项,所得的商叫做比值。比值跟除法的商是一样的,可以用分数表示、也可以用小数表示。
课件出示:前项、后项、比号、比值。
[设计意图:比的定义是规定的,很难让学生探究得出,因此,借助历史资料,我让学生在阅读中感悟,自己说说哪一句话其实就是比的意义,再用字母来表示这句话的意思。比的读法和写法、比各部份的名称,这两个知识点对学生来说并不是很难掌握,因此,我先让学生自学课本,在自学的基础上进行交流,在交流的过程中弥补自学过程中理解不到位的问题,培养学生自主学习的能力,让学生体验自主探索的乐趣。]
三、走进生活,在具体实例中深入理解比表示的意思。
师:为了让同学们了解生活中的比,郭老师决定带同学们到生活中去看一看,喜欢吗?
1、第1站——走进饮料店
师:谁来介绍一下,这家店的奶茶是怎样调制成的?
师:是5比1吗?怎么验证。
再出示:
师:对比这两种说法,你有什么想法?
(应用了比,能更清楚地反映奶与巧克力的质量之间的倍数关系。)(更简洁)
2、第二站——观看马拉松比赛
马拉松选手跑40千米,大约需2时
师:看到这个情境,你想到了什么问题?要求速度应该怎么算?(路程÷时间=速度)
怎么列式?
路程÷时间还可以怎么表示?路程与速度的比是( )比( ),比值表示什么?
3、第三站——走进水果店
师:我们到了水果店,有A、B、C三个摊位,你会选择哪一个摊位买苹果?
师:要比较哪一个摊位的苹果便宜也就是要比什么?(单价)要求单价怎么求呢?(总价÷数量=单价)
师:请你写出A、B、C三个摊位苹果的总价与数量的比,并算出比值。
学生在课堂练习本上独立写。
全班交流
师:要比较哪个摊位的苹果便宜,实际上就是要比较什么?(比值)
在这里,比值表示什么?
4、第4站——游览北京世界公园。
法国埃菲尔铁塔的高度是320米,北京世界公园的埃菲尔铁塔的高大约是32米,北京世界公园的埃菲尔铁塔的高度与法国埃菲尔铁塔的高度的比是( )∶( )。
可能出示的答案:
1∶10 10∶1 32 ∶320
师:同意1∶10的同学请举手,你们是怎么想的?
5、回顾反思
出示前面出现的4个比
师:现在让我们一起来回顾刚才我们在生活中找到的比。
请个别学生说一说这些比表示的意思。
6、观察对比
师:仔细观察、认真思考,这四个比,有什么相同点,有什么不同点?请同学们先在小组里讨论一下。
全班交流。
师:如果要把这四个比分成两类,可以怎么分?
(1、4一类,表示两个数之间的倍数关系;2、3一类,两个不同类量相比,产生一个新的量。无论是表示倍数关系的比,还是产生新的量的比都是由除法计算得出的,因此,两个数相除,又叫做这两个数的比)
[设计意图:为了让学生理解比是表示两种数量之间相除的关系,我通过四个生活情境让学生体验,其中“走进饮料店” 、“游览北京世界公园”体现的是同类量的比,“观看马拉松比赛”、“走进水果店”体现的是不同类量的比,在教学时从学生已有的生活经验入手,先让学生尝试用比来表示数量间的关系,再用除法进行验证,使学生进一步体会到比是怎么得到的、明确比与除法之间有密切的关系。接着再让学生回顾反思这四个比表示的意思,在这基础上,让学生比较这四个比的异同点,从而让学生感悟到无论是表示倍数关系的比,还是产生新的量的比都是由除法计算得出的,再一次让学生理解比最本质的意义。]
四、结合比赛,在练一练中巩固比的意义。
师:现在,比的意义你们都理解了吗?还有什么问题?接下来我们来进行一个比赛怎样?
请看比赛规则:
比赛规则1、男、女生比赛,轮流回答。2、答对一题,加10分,答错一题倒扣5分。3、得分高的一方获胜。
(1)小强的身高1米,他爸爸的身高是173厘米,小强说他和他爸爸的身高比是1 ︰ 173,对不对?如果不对,你认为是多少呢?
(2)王叔叔2小时加工了30个零件,王叔叔的工作总量与工作时间的比是( ︰ ),比值是( ),比值表示( )。
(3)跑36千米大约需要2时,路程与时间的比大约是( ︰ ),比值是( ),比值表示( )。
(4)足球比赛中常出现“2︰0,它是一个比吗?
(5)调制一种蜜水,3杯蜂蜜要18杯水,水与蜂蜜的比是3︰18,这样说对吗?为什么?。
(6)福尔摩斯侦探术
人的脚长与身高的比是1∶7
福尔摩斯发现一个脚印长25厘米,他可以做出什么样的推断?
(7)小资料
上图是古希腊雅典古城巴台农神庙的剖面图,在其周围描出一个长方形。我们发现,它的宽与长的比值大约是0.618,这个比称为黄金分割比。
著名天文学家开普勒称黄金分割是“几何学中的一大宝藏”,黄金分割比被广泛应用于建筑、绘画等方面。黄金分割比究竟蕴藏着怎样的秘密,你想揭开它的神秘面纱吗?
[设计意图:为了提高学生学习的积极性,在这里采用了竞赛活动的教学策略。让学生在竞赛活动中应用这节课所学的知识解决数学问题。在解决问题的过程中让学生感受“比”和实际生活的密切联系,进一步体会比的意义和价值。]
五、回顾反思,全课小结。
师:通过这节课的学习,你有什么收获呢?
50
200
300
100
单位:米
⑥
⑤
④
③
②
①
自学提纲
1、用数学方法如何写比,如何读呢?
2、比的各部分的名称分别叫什么?
一种巧克力奶是由巧克力与奶调制成的,如果奶有100克就要加入20克巧克力;如果奶有200克就要加入40克巧克力;如果奶有300克就要加入60克巧克力;如果奶有400克就要加入80克巧克力;……
一种巧克力奶是由巧克力与奶调制成的,奶与巧克力的质量比是5比1。
教学内容:
义务教育课程标准实验教科书(北师大版)小学数学第十一册P48——50。
教材分析
《生活中的比》是在学生已经学过除法的意义、分数的意义以及分数与除法的关系的基础上学习的,是《比的认识》这一单元的起始课。比在数学中是一个重要的概念,体会比的意义和价值是教材内容的数学核心思想。教材以系列情境为学生理解比的意义提供了丰富的直观背景和具体案例。但要用足用好这些情境,真正达到帮助学生理解比的本质的目的,需要创造性地使用教材。因此,本课的教学设计在教学内容的处理方面有以下几点思考:
1、创设问题情境,帮助学生在具体的情境中抽象出比的意义,初步体会学习比的必要性、为引出比的意义做好铺垫。
2、根据历史资料引出比的意义,再以生活为主线,让学生在生活实例中体验比与除法的关系
教学目标
知识目标:经历从具体情境中抽象出比的过程,理解比的意义、能正确读写比、认识比各部份的名称。
能力目标:能利用比的知识解释一些简单的生活问题。
情感目标:感受比在生活中的广泛存在。
教学重点
理解比的意义。
教学难点
理解比的意义。
教学过程
一、创设情境,在情境中体会引入比的必要性,初步感知比的意义。
1、出示情境1。
师:这是小红上学和放学回家的路线图,你认为这幅图画得合理吗?为什么?
师:画线段图的时候,要根据实据实际情况,实际距离比较长,画的线条就要长一些,实际距离短,画的线条就短。
[设计意图:借助学生已有的画路线图的经验,让学生感悟画线段图时要根据实据情况,路程长的画的线段就长,路程短的画的线段就短,为下面的一个情境做好铺垫。]
2、出示情境2
师:我们学校有一片空地,学校想在空地上建一个长2米、宽1米的长方形花圃,这是我们学校的几位同学画的设计图,你觉得哪几张设计图画得比较像呢?
3、讨论交流。
师:为什么2号、3号、6号设计图画得不像呢?
为什么这1号、4号、5号设计图会比较像呢?究竟蕴藏差怎样的秘密呢?
观察这几个长方形,在小组里说一说你发现了什么?
学生小组交流
全班交流
可能出现的答案:
这几个长方形的长都是宽的1.5倍。
这几个长方形的宽是长的三分之二。
……
4、还可以怎么画。
师:如果让同学们也来画这个花圃的设计图,还可以怎么画呢?
学生汇报。
师:画得完吗?(……)
师:观察这组数据,什么在变,什么没变?
(长与宽的厘米数在变,长与宽之间的倍数关系没变)
师:那么这些长方形的长与宽之间存在着怎样的关系呢?
学生个别回答。
师:这可以用一种新的表示方法——比。我们可以说这些长方形长与宽的比是(3)比( 2)。
花圃的长3米,宽2米,我们在画花圃的设计图时只要按长与宽的比是3比2来画就会画得像,其实设计师画在画设计图时也要应用到这个知识。
揭示课题——生活中的比
[设计意图:这一环节通过数形结合,让学生辨别哪张设计图画得好,引导学生探索长方形的长与宽之间的关系,发现1号、4号、5号长方形的长与宽存在着固定的倍数关系,再让学生接着画花圃的设计图,学生通过画设计图,体会到长方形的长与宽的厘米数在变,但长与宽之间的倍数关系没有变,怎样用一句话来总结这些长方形共同的特点呢?出此引出比,使学生对“比”有初步的体验,同时,让学生体会到引入比的必要性。]
二、引用历史资料,揭示比的意义,自学比的读写、比各部份的名称。
1、揭示比的意义。
师:比与我们学过的哪些知识有关联呢?让我们一起来看看著名数学家莱布尼兹是怎么说的。
课件出示——你知道吗?
十七世纪,著名数学家莱布尼兹认为,因为两个数相除又叫做两个数的比,所以比号与除号有一种亲缘关系。而比号与除号又不能共用,所以就把 “÷ ” 中的小横线去掉,于是“∶”就成为了比号。
师:现在你知道什么叫做比吗
板书:两个数相除,又叫做这两个数的比。
师:从这段话中你还知道了什么?(比号的写法)
如果用a÷b表示“两个数相除”, a比b该怎么写呢?
师:a、b可以是任意一个数吗?为什么?
板书:b≠0
2、学生带着问题自学课本。
师:现在请同学们打开课本,翻到第50页,划出比的定义。
师:再请同学们带着这两个问题自学课本。
3、全班交流。
师:通过自学,你还知道了什么?
课件出示:
6÷4写作 6:4 读作 6比4
师强调:比号前面的数叫做比的前项,比号后面的数叫做比的后项。用比的前项除以比的后项,所得的商叫做比值。比值跟除法的商是一样的,可以用分数表示、也可以用小数表示。
课件出示:前项、后项、比号、比值。
[设计意图:比的定义是规定的,很难让学生探究得出,因此,借助历史资料,我让学生在阅读中感悟,自己说说哪一句话其实就是比的意义,再用字母来表示这句话的意思。比的读法和写法、比各部份的名称,这两个知识点对学生来说并不是很难掌握,因此,我先让学生自学课本,在自学的基础上进行交流,在交流的过程中弥补自学过程中理解不到位的问题,培养学生自主学习的能力,让学生体验自主探索的乐趣。]
三、走进生活,在具体实例中深入理解比表示的意思。
师:为了让同学们了解生活中的比,郭老师决定带同学们到生活中去看一看,喜欢吗?
1、第1站——走进饮料店
师:谁来介绍一下,这家店的奶茶是怎样调制成的?
师:是5比1吗?怎么验证。
再出示:
师:对比这两种说法,你有什么想法?
(应用了比,能更清楚地反映奶与巧克力的质量之间的倍数关系。)(更简洁)
2、第二站——观看马拉松比赛
马拉松选手跑40千米,大约需2时
师:看到这个情境,你想到了什么问题?要求速度应该怎么算?(路程÷时间=速度)
怎么列式?
路程÷时间还可以怎么表示?路程与速度的比是( )比( ),比值表示什么?
3、第三站——走进水果店
师:我们到了水果店,有A、B、C三个摊位,你会选择哪一个摊位买苹果?
师:要比较哪一个摊位的苹果便宜也就是要比什么?(单价)要求单价怎么求呢?(总价÷数量=单价)
师:请你写出A、B、C三个摊位苹果的总价与数量的比,并算出比值。
学生在课堂练习本上独立写。
全班交流
师:要比较哪个摊位的苹果便宜,实际上就是要比较什么?(比值)
在这里,比值表示什么?
4、第4站——游览北京世界公园。
法国埃菲尔铁塔的高度是320米,北京世界公园的埃菲尔铁塔的高大约是32米,北京世界公园的埃菲尔铁塔的高度与法国埃菲尔铁塔的高度的比是( )∶( )。
可能出示的答案:
1∶10 10∶1 32 ∶320
师:同意1∶10的同学请举手,你们是怎么想的?
5、回顾反思
出示前面出现的4个比
师:现在让我们一起来回顾刚才我们在生活中找到的比。
请个别学生说一说这些比表示的意思。
6、观察对比
师:仔细观察、认真思考,这四个比,有什么相同点,有什么不同点?请同学们先在小组里讨论一下。
全班交流。
师:如果要把这四个比分成两类,可以怎么分?
(1、4一类,表示两个数之间的倍数关系;2、3一类,两个不同类量相比,产生一个新的量。无论是表示倍数关系的比,还是产生新的量的比都是由除法计算得出的,因此,两个数相除,又叫做这两个数的比)
[设计意图:为了让学生理解比是表示两种数量之间相除的关系,我通过四个生活情境让学生体验,其中“走进饮料店” 、“游览北京世界公园”体现的是同类量的比,“观看马拉松比赛”、“走进水果店”体现的是不同类量的比,在教学时从学生已有的生活经验入手,先让学生尝试用比来表示数量间的关系,再用除法进行验证,使学生进一步体会到比是怎么得到的、明确比与除法之间有密切的关系。接着再让学生回顾反思这四个比表示的意思,在这基础上,让学生比较这四个比的异同点,从而让学生感悟到无论是表示倍数关系的比,还是产生新的量的比都是由除法计算得出的,再一次让学生理解比最本质的意义。]
四、结合比赛,在练一练中巩固比的意义。
师:现在,比的意义你们都理解了吗?还有什么问题?接下来我们来进行一个比赛怎样?
请看比赛规则:
比赛规则1、男、女生比赛,轮流回答。2、答对一题,加10分,答错一题倒扣5分。3、得分高的一方获胜。
(1)小强的身高1米,他爸爸的身高是173厘米,小强说他和他爸爸的身高比是1 ︰ 173,对不对?如果不对,你认为是多少呢?
(2)王叔叔2小时加工了30个零件,王叔叔的工作总量与工作时间的比是( ︰ ),比值是( ),比值表示( )。
(3)跑36千米大约需要2时,路程与时间的比大约是( ︰ ),比值是( ),比值表示( )。
(4)足球比赛中常出现“2︰0,它是一个比吗?
(5)调制一种蜜水,3杯蜂蜜要18杯水,水与蜂蜜的比是3︰18,这样说对吗?为什么?。
(6)福尔摩斯侦探术
人的脚长与身高的比是1∶7
福尔摩斯发现一个脚印长25厘米,他可以做出什么样的推断?
(7)小资料
上图是古希腊雅典古城巴台农神庙的剖面图,在其周围描出一个长方形。我们发现,它的宽与长的比值大约是0.618,这个比称为黄金分割比。
著名天文学家开普勒称黄金分割是“几何学中的一大宝藏”,黄金分割比被广泛应用于建筑、绘画等方面。黄金分割比究竟蕴藏着怎样的秘密,你想揭开它的神秘面纱吗?
[设计意图:为了提高学生学习的积极性,在这里采用了竞赛活动的教学策略。让学生在竞赛活动中应用这节课所学的知识解决数学问题。在解决问题的过程中让学生感受“比”和实际生活的密切联系,进一步体会比的意义和价值。]
五、回顾反思,全课小结。
师:通过这节课的学习,你有什么收获呢?
50
200
300
100
单位:米
⑥
⑤
④
③
②
①
自学提纲
1、用数学方法如何写比,如何读呢?
2、比的各部分的名称分别叫什么?
一种巧克力奶是由巧克力与奶调制成的,如果奶有100克就要加入20克巧克力;如果奶有200克就要加入40克巧克力;如果奶有300克就要加入60克巧克力;如果奶有400克就要加入80克巧克力;……
一种巧克力奶是由巧克力与奶调制成的,奶与巧克力的质量比是5比1。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
