2021-2022学年数学人教A版(2019)必修第一册5.1.1 任意角 学案
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)必修第一册5.1.1 任意角 学案 |
|
|
| 格式 | docx | ||
| 文件大小 | 300.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 09:54:09 | ||
图片预览


文档简介
三角函数
5.1.1任意角
学习目标:
1.通过实例展示,使学生理解角的概念推广的必要性;
2.让学生理解并掌握正角、负角、零角、象限角的概念;
3.让学生掌握终边相同的角的表示方法.
一、创设情景,引出问题
问题:初中我们是如何定义角的?角的范围是什么?都学过哪些角?
1、上周六我们学校承担了一项考试,每次考试之前,每个考场都有一项必做的工作,校准时间.若一个考场里的表慢了10分钟,我们将如何校准?在校准时,分针旋转多少度?
2、若是表快了5分钟,我们将如何校准?在校准时,分针旋转多少度?
3、若是慢了一个半小时,我们将如何校准?在校准时,分针旋转多少度?
二、通过对比,获得新知
角的定义:__________________________________________
正角:__________________________________________
负角:__________________________________________
零角:__________________________________________
注:1、角或可以简记成.
刻画角的关键是旋转量、旋转方向.
如果两个角的旋转量相同、旋转方向也相同,我们就称这两个角相等.
4、如果两个角的旋转量相同、旋转方向不同,我们就称这两个角互为相反角.
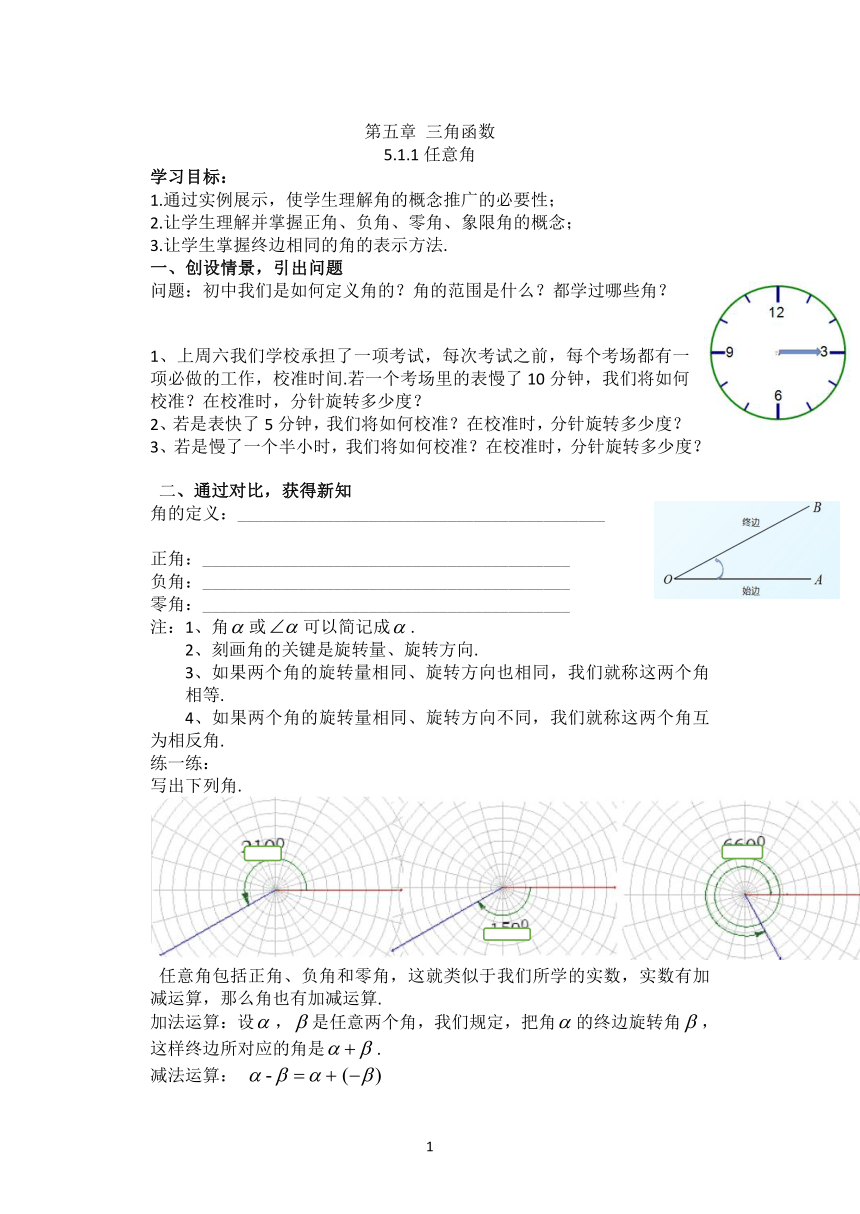
练一练:
写出下列角.
任意角包括正角、负角和零角,这就类似于我们所学的实数,实数有加减运算,那么角也有加减运算.
加法运算:设,是任意两个角,我们规定,把角的终边旋转角,这样终边所对应的角是.
减法运算:
三、合作探究,共获新知
为了更好的研究角,我们需要一个统一的标准,也为了更好地表现角周而复始的变化规律,所以我们通常把角放在直角坐标系中研究.
象限角:使角的顶点与原点重合,角的始边与轴非负半轴重合,角的终边落在第几象限,就说这个角是第几象限角.
象限角分类:__________________________________________
轴线角:__________________________________________
注意:将角放在直角坐标系中,将角的始边与轴非负半轴重合.
练一练:
1、在同一平面直角坐标系中画出以下几个角,并说出分别是第几象限角.
思考1:在做以上练习时,我们发现、、这三个角的终边都是同一条射线,它们的终边相同.你还能找出哪些以这一条射线为终边的角?与终边相同的角与有什么关系?
思考2:与终边相同的角的集合如何表示?
练一练:终边落在轴非正半轴的角的集合如何表示?
问题:如何表示与终边相同的角的集合?
四、新知应用,深入理解
例1、在范围内,找到与角终边相同的角,并判断它是第几象限角.
变式、在 范围内,找到与角终边相同的角,并判断它是第几象限角.
写出终边落在直线上的角的集合.中满足不等式的元素有哪些?
五、当堂检测
1.下列角中,终边在轴非负半轴上的是( )
A. B.90°
C.180° D.270°
2.下列各个角中与角2 021°终边相同的角的度数是( )
A.-149° B.679°
C.321° D.221°
3.角-870°的终边所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.50°角的始边与轴的非负半轴重合,把终边按顺时针方向旋转2周,所得角是________.
六、课堂小结
1、这节课学习了哪些知识?
2、利用哪些方法学习的?
3、学习了哪些技能?
4、还有哪些疑惑?
七、作业
1、课本第171页题.
2、根据这节课所学知识,自己编一道题,并且写出命制这一道题的意图,写出解题步骤.
思考题:已知角在第一象限,能否判断在第几象限?
明日歌
明日复明日,明日何其多?
我生待明日,万事成蹉跎。
世人皆被明日累,春去秋来老将至。
朝看水东流,暮看日西坠。
百年明日能几何?请君听我明日歌。
5.1.1任意角
学习目标:
1.通过实例展示,使学生理解角的概念推广的必要性;
2.让学生理解并掌握正角、负角、零角、象限角的概念;
3.让学生掌握终边相同的角的表示方法.
一、创设情景,引出问题
问题:初中我们是如何定义角的?角的范围是什么?都学过哪些角?
1、上周六我们学校承担了一项考试,每次考试之前,每个考场都有一项必做的工作,校准时间.若一个考场里的表慢了10分钟,我们将如何校准?在校准时,分针旋转多少度?
2、若是表快了5分钟,我们将如何校准?在校准时,分针旋转多少度?
3、若是慢了一个半小时,我们将如何校准?在校准时,分针旋转多少度?
二、通过对比,获得新知
角的定义:__________________________________________
正角:__________________________________________
负角:__________________________________________
零角:__________________________________________
注:1、角或可以简记成.
刻画角的关键是旋转量、旋转方向.
如果两个角的旋转量相同、旋转方向也相同,我们就称这两个角相等.
4、如果两个角的旋转量相同、旋转方向不同,我们就称这两个角互为相反角.
练一练:
写出下列角.
任意角包括正角、负角和零角,这就类似于我们所学的实数,实数有加减运算,那么角也有加减运算.
加法运算:设,是任意两个角,我们规定,把角的终边旋转角,这样终边所对应的角是.
减法运算:
三、合作探究,共获新知
为了更好的研究角,我们需要一个统一的标准,也为了更好地表现角周而复始的变化规律,所以我们通常把角放在直角坐标系中研究.
象限角:使角的顶点与原点重合,角的始边与轴非负半轴重合,角的终边落在第几象限,就说这个角是第几象限角.
象限角分类:__________________________________________
轴线角:__________________________________________
注意:将角放在直角坐标系中,将角的始边与轴非负半轴重合.
练一练:
1、在同一平面直角坐标系中画出以下几个角,并说出分别是第几象限角.
思考1:在做以上练习时,我们发现、、这三个角的终边都是同一条射线,它们的终边相同.你还能找出哪些以这一条射线为终边的角?与终边相同的角与有什么关系?
思考2:与终边相同的角的集合如何表示?
练一练:终边落在轴非正半轴的角的集合如何表示?
问题:如何表示与终边相同的角的集合?
四、新知应用,深入理解
例1、在范围内,找到与角终边相同的角,并判断它是第几象限角.
变式、在 范围内,找到与角终边相同的角,并判断它是第几象限角.
写出终边落在直线上的角的集合.中满足不等式的元素有哪些?
五、当堂检测
1.下列角中,终边在轴非负半轴上的是( )
A. B.90°
C.180° D.270°
2.下列各个角中与角2 021°终边相同的角的度数是( )
A.-149° B.679°
C.321° D.221°
3.角-870°的终边所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.50°角的始边与轴的非负半轴重合,把终边按顺时针方向旋转2周,所得角是________.
六、课堂小结
1、这节课学习了哪些知识?
2、利用哪些方法学习的?
3、学习了哪些技能?
4、还有哪些疑惑?
七、作业
1、课本第171页题.
2、根据这节课所学知识,自己编一道题,并且写出命制这一道题的意图,写出解题步骤.
思考题:已知角在第一象限,能否判断在第几象限?
明日歌
明日复明日,明日何其多?
我生待明日,万事成蹉跎。
世人皆被明日累,春去秋来老将至。
朝看水东流,暮看日西坠。
百年明日能几何?请君听我明日歌。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
