1.5.1弹性碰撞和非弹性碰撞(课件)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理 选择性必修 第一册 (共25张PPT)
文档属性
| 名称 | 1.5.1弹性碰撞和非弹性碰撞(课件)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理 选择性必修 第一册 (共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-26 10:07:26 | ||
图片预览







文档简介
(共25张PPT)
人教版(2019)高中物理选择性必修第一册
第一章 动量守恒定律
1.5.1 弹性碰撞和非弹性碰撞
授课人:扬帆起航
CONTENTS
01
碰撞的分类
02
弹性碰撞
03
碰撞三原则
04
典型例题
目录
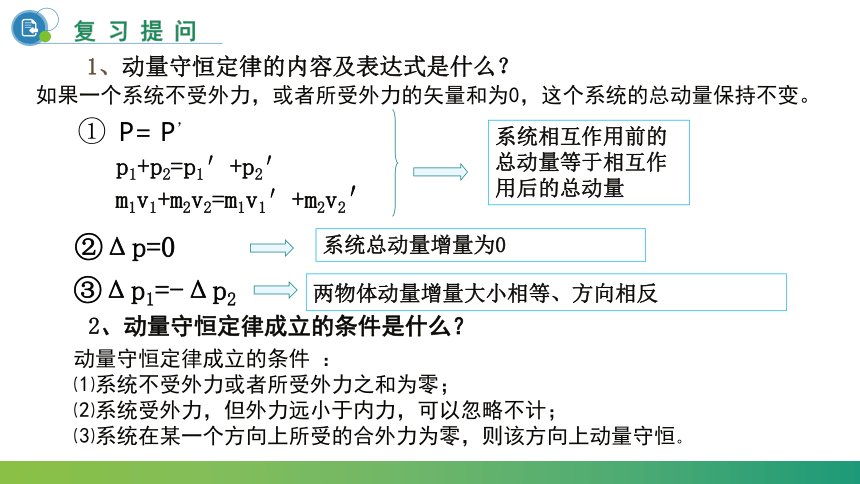
复习提问
2、动量守恒定律成立的条件是什么?
1、动量守恒定律的内容及表达式是什么?
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
动量守恒定律成立的条件 :
⑴系统不受外力或者所受外力之和为零;
⑵系统受外力,但外力远小于内力,可以忽略不计;
⑶系统在某一个方向上所受的合外力为零,则该方向上动量守恒。
① P= P’
p1+p2=p1′+p2′
m1v1+m2v2=m1v1′+m2v2′
系统相互作用前的总动量等于相互作用后的总动量
②Δp=0
系统总动量增量为0
③Δp1=-Δp2
两物体动量增量大小相等、方向相反
01
碰撞的分类
按照机械能是否守恒、碰撞前后速度是否共线可以进行分类
动量守恒定律
碰撞指的是两个物体在_____内发生相互作用,由于相互碰撞的物体组成的系统,外力通常远小于内力,可以忽略不计,系统在碰撞过程中_____
关于碰撞前和碰撞后的含义
碰撞前指的是__________ ,而不是发生碰撞前的某一时刻.
碰撞后指的是 __________ , 而不是发生碰撞后的某一时刻.
即将发生碰撞那一时刻
碰撞刚刚结束的那一时刻
很短的时间
动量守恒
碰 撞
碰撞过程的特点:
1、时间特点:在碰撞过程中,相互作用时间很短( △t→0) ;
2、作用力特点:在碰撞过程中,相互作用力即内力先急剧增大,后急剧减小,平均作用力很大;
3、位移特点:由于碰撞是在瞬间完成的,故可以认为碰撞前后,物体仍在原来的位置,即位移不变。并且,其他与碰撞物体相联系,但不直接参与碰撞的物体,其运动状态仍保持不变。
4、碰撞系统动量的特点:
将碰撞双方包括在同一系统内,系统的总动量(近似)守恒。
5、能量特点:
v1
m1
m2
一 按碰撞前后能量变化分类
1.弹性碰撞:
(1)定义:碰撞过程中机械能守恒的碰撞
3.完全非弹性碰撞(碰撞后两物体连在一起):
动量守恒,机械能损失最大
例如钢球、玻璃球的碰撞
(2)规律:
动量守恒
机械能守恒
2.非弹性碰撞:
(1)定义:碰撞过程中机械能不守恒的碰撞
3.完全非弹性碰撞(碰撞后两物体连在一起):
动量守恒,机械能损失最大
例如木制品、橡皮泥球的碰撞
(2)规律:
动量守恒
(3)完全非弹性碰撞:机械能损失最多
机械能有损失
或者
动量守恒
机械能损失最大
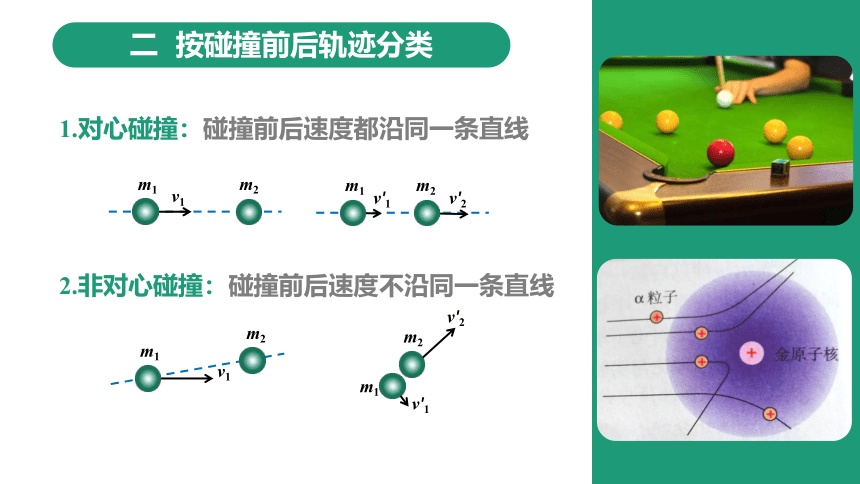
二 按碰撞前后轨迹分类
1.对心碰撞:碰撞前后速度都沿同一条直线
2.非对心碰撞:碰撞前后速度不沿同一条直线
v'1
m1
m2
v'2
v1
m1
m2
v1
m1
m2
v'1
m1
m2
v'2
02
弹性碰撞
动量守恒定律
用方程表达弹性碰撞的规律,并对最终结果进行实际分析
动量守恒
机械能守恒
整理得
解得
1球趋近2球的相对速度
(接近速度)
2球远离1球的相对速度
(分离速度)
等于
弹性碰撞的规律
解得
1球末速度
2球末速度
特殊情况:运动物体碰撞静止物体
即v1≠0,v2=0时,有
1球末速度
2球末速度
碰撞规律不难记
两项相加是规律;
一 二 一,二 二 二;
分母都是1+2;
要问v‘2 是多少;
角标互换就可以;
1换2,2换1
弹性碰撞的规律
碰后实现动量和动能的全部转移(即交换了速度)
碰后m1速度几乎没变,仍按原速度运动 ,质量小物体以m1的速度的两倍向前运动。
碰后m1被按原来速率弹回,m2几乎末动。
1.m1=m2
2.m1>>m2
3.m1<4.m1>m2,v1′>0,v2 ′>0,碰撞后两球都向前运动.
5.m1<m2,v1 ′<0,v2 ′>0碰撞后质量小的球被反弹回去.
弹性碰撞的规律
例1 速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
解:由于是弹性碰撞,根据动量守恒和机械能守恒得
塑料球:
钢球:
与塑料球初速度方向相反
与塑料球初速度方向相同
典例探究
03
碰撞三原则
动量守恒定律
系统动量要守恒;机械能不增加;速度要合理
1.系统动量守恒原则:碰撞前后系统的总动量守恒.
2.动能不增加原则:碰撞后系统的总动能小于或等于碰撞前系统的总动能,即系统的总动能不增加.
3.物理情景可行性原则:若碰后两物体同向运动,则碰撞后后面物体的速度一定小于或等于前面物体的速度(否则碰撞没有结束,还要发生碰撞).
v1
m1
m2
v1′
m1
m2
v2′
例2 质量相等的 A、B 两球在光滑水平桌面上沿同一直线、同一方向运动,A 球的动量是 7 kg·m/s,B 球的动量是 5 kg·m/s, A 球追上 B 球发生碰撞,碰撞后两球的动量可能值是( )
A. pA = 6 kg·m/s, pB' = 6 kg·m/s
B. pA = 3 kg·m/s, pB' = 9 kg·m/s
C. pA =2 kg·m/s, pB' = 14 kg·m/s
D. pA = 4 kg·m/s,pB' = 17 kg·m/s
A
典例探究
分析讲解:
碰撞过程动量守恒,
知:A、B、C都满足.
,知:A、B、C也都满足.
总动能不能增加,即
得:只有A正确了
04
典型例题
动量守恒定律
结合课后习题及变式训练巩固本节课所学的知识
在气垫导轨上,一个质量为400g的滑块以15cm/s的速度与另一个质量为200g,速度为10cm/s并沿反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1)求碰撞后滑块速度的大小和方向.
(2)这次碰撞,两滑块共损失了多少机械能?
课堂练习1
解:(1)以400g的滑块的初速度方向为正方向,根据动量守恒定律
(2)损失的机械能:
一 种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.4×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.中子的质量与氢原子核的质量mH有什么关系.
【查德威克发现中子实验】
碰后氮原子核的速度为:
解:设未知粒子质量m,速度v,它与氢和氮原子核碰撞都是弹性的,碰后氢原子核的速度为:
两式联立,解得未知粒子的质量为mH
课堂练习2
在光滑水平面上,动能为E0 ,动量大小为p0 的小钢球1与静止的小钢球2发生碰撞,碰撞前后球1的运动方向相反,将碰后球1的动能和动量大小分别记为 E1、p1,球2的动能和动量大小分别记为E2、p2,则必有 ( )
A. E1 < E0 B. p1 < p0
C. E2 > E0 D. p2 > p0
ABD
课堂练习3
如图甲所示,在光滑水平面上的两小球发生正碰。小球的质量分别为 m1 和 m2。图乙为它们碰撞前后的 s t (位移 ─ 时间) 图象。已知 m1 = 0.1 kg。由此可以判断 ( )
A. 碰前 m2 静止,m1 向右运动
B. 碰后 m2 和 m1 都向右运动
C. m2 = 0.3 kg
D. 碰撞过程中系统损失了 0.4 J 的机械能
AC
课堂练习4
质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能是以下值吗?
(A)0.6v (B)0.4v (C)0.2v
解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:
B球速度的最大值发生在弹性碰撞时:
∵所以,只有0.4v是速度可能值
课堂练习5
1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
2. 非弹性碰撞:碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。
(1) 规律:动量守恒,机械能减少
(2) 能量转化情况:完全非弹性碰撞中系统动能损失最大
3. 对心碰撞和非对心碰撞
课堂总结
4.微观粒子的碰撞---散射
人教版(2019)高中物理选择性必修第一册
第一章 动量守恒定律
1.5.1 弹性碰撞和非弹性碰撞
授课人:扬帆起航
CONTENTS
01
碰撞的分类
02
弹性碰撞
03
碰撞三原则
04
典型例题
目录
复习提问
2、动量守恒定律成立的条件是什么?
1、动量守恒定律的内容及表达式是什么?
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
动量守恒定律成立的条件 :
⑴系统不受外力或者所受外力之和为零;
⑵系统受外力,但外力远小于内力,可以忽略不计;
⑶系统在某一个方向上所受的合外力为零,则该方向上动量守恒。
① P= P’
p1+p2=p1′+p2′
m1v1+m2v2=m1v1′+m2v2′
系统相互作用前的总动量等于相互作用后的总动量
②Δp=0
系统总动量增量为0
③Δp1=-Δp2
两物体动量增量大小相等、方向相反
01
碰撞的分类
按照机械能是否守恒、碰撞前后速度是否共线可以进行分类
动量守恒定律
碰撞指的是两个物体在_____内发生相互作用,由于相互碰撞的物体组成的系统,外力通常远小于内力,可以忽略不计,系统在碰撞过程中_____
关于碰撞前和碰撞后的含义
碰撞前指的是__________ ,而不是发生碰撞前的某一时刻.
碰撞后指的是 __________ , 而不是发生碰撞后的某一时刻.
即将发生碰撞那一时刻
碰撞刚刚结束的那一时刻
很短的时间
动量守恒
碰 撞
碰撞过程的特点:
1、时间特点:在碰撞过程中,相互作用时间很短( △t→0) ;
2、作用力特点:在碰撞过程中,相互作用力即内力先急剧增大,后急剧减小,平均作用力很大;
3、位移特点:由于碰撞是在瞬间完成的,故可以认为碰撞前后,物体仍在原来的位置,即位移不变。并且,其他与碰撞物体相联系,但不直接参与碰撞的物体,其运动状态仍保持不变。
4、碰撞系统动量的特点:
将碰撞双方包括在同一系统内,系统的总动量(近似)守恒。
5、能量特点:
v1
m1
m2
一 按碰撞前后能量变化分类
1.弹性碰撞:
(1)定义:碰撞过程中机械能守恒的碰撞
3.完全非弹性碰撞(碰撞后两物体连在一起):
动量守恒,机械能损失最大
例如钢球、玻璃球的碰撞
(2)规律:
动量守恒
机械能守恒
2.非弹性碰撞:
(1)定义:碰撞过程中机械能不守恒的碰撞
3.完全非弹性碰撞(碰撞后两物体连在一起):
动量守恒,机械能损失最大
例如木制品、橡皮泥球的碰撞
(2)规律:
动量守恒
(3)完全非弹性碰撞:机械能损失最多
机械能有损失
或者
动量守恒
机械能损失最大
二 按碰撞前后轨迹分类
1.对心碰撞:碰撞前后速度都沿同一条直线
2.非对心碰撞:碰撞前后速度不沿同一条直线
v'1
m1
m2
v'2
v1
m1
m2
v1
m1
m2
v'1
m1
m2
v'2
02
弹性碰撞
动量守恒定律
用方程表达弹性碰撞的规律,并对最终结果进行实际分析
动量守恒
机械能守恒
整理得
解得
1球趋近2球的相对速度
(接近速度)
2球远离1球的相对速度
(分离速度)
等于
弹性碰撞的规律
解得
1球末速度
2球末速度
特殊情况:运动物体碰撞静止物体
即v1≠0,v2=0时,有
1球末速度
2球末速度
碰撞规律不难记
两项相加是规律;
一 二 一,二 二 二;
分母都是1+2;
要问v‘2 是多少;
角标互换就可以;
1换2,2换1
弹性碰撞的规律
碰后实现动量和动能的全部转移(即交换了速度)
碰后m1速度几乎没变,仍按原速度运动 ,质量小物体以m1的速度的两倍向前运动。
碰后m1被按原来速率弹回,m2几乎末动。
1.m1=m2
2.m1>>m2
3.m1<
5.m1<m2,v1 ′<0,v2 ′>0碰撞后质量小的球被反弹回去.
弹性碰撞的规律
例1 速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
解:由于是弹性碰撞,根据动量守恒和机械能守恒得
塑料球:
钢球:
与塑料球初速度方向相反
与塑料球初速度方向相同
典例探究
03
碰撞三原则
动量守恒定律
系统动量要守恒;机械能不增加;速度要合理
1.系统动量守恒原则:碰撞前后系统的总动量守恒.
2.动能不增加原则:碰撞后系统的总动能小于或等于碰撞前系统的总动能,即系统的总动能不增加.
3.物理情景可行性原则:若碰后两物体同向运动,则碰撞后后面物体的速度一定小于或等于前面物体的速度(否则碰撞没有结束,还要发生碰撞).
v1
m1
m2
v1′
m1
m2
v2′
例2 质量相等的 A、B 两球在光滑水平桌面上沿同一直线、同一方向运动,A 球的动量是 7 kg·m/s,B 球的动量是 5 kg·m/s, A 球追上 B 球发生碰撞,碰撞后两球的动量可能值是( )
A. pA = 6 kg·m/s, pB' = 6 kg·m/s
B. pA = 3 kg·m/s, pB' = 9 kg·m/s
C. pA =2 kg·m/s, pB' = 14 kg·m/s
D. pA = 4 kg·m/s,pB' = 17 kg·m/s
A
典例探究
分析讲解:
碰撞过程动量守恒,
知:A、B、C都满足.
,知:A、B、C也都满足.
总动能不能增加,即
得:只有A正确了
04
典型例题
动量守恒定律
结合课后习题及变式训练巩固本节课所学的知识
在气垫导轨上,一个质量为400g的滑块以15cm/s的速度与另一个质量为200g,速度为10cm/s并沿反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1)求碰撞后滑块速度的大小和方向.
(2)这次碰撞,两滑块共损失了多少机械能?
课堂练习1
解:(1)以400g的滑块的初速度方向为正方向,根据动量守恒定律
(2)损失的机械能:
一 种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.4×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.中子的质量与氢原子核的质量mH有什么关系.
【查德威克发现中子实验】
碰后氮原子核的速度为:
解:设未知粒子质量m,速度v,它与氢和氮原子核碰撞都是弹性的,碰后氢原子核的速度为:
两式联立,解得未知粒子的质量为mH
课堂练习2
在光滑水平面上,动能为E0 ,动量大小为p0 的小钢球1与静止的小钢球2发生碰撞,碰撞前后球1的运动方向相反,将碰后球1的动能和动量大小分别记为 E1、p1,球2的动能和动量大小分别记为E2、p2,则必有 ( )
A. E1 < E0 B. p1 < p0
C. E2 > E0 D. p2 > p0
ABD
课堂练习3
如图甲所示,在光滑水平面上的两小球发生正碰。小球的质量分别为 m1 和 m2。图乙为它们碰撞前后的 s t (位移 ─ 时间) 图象。已知 m1 = 0.1 kg。由此可以判断 ( )
A. 碰前 m2 静止,m1 向右运动
B. 碰后 m2 和 m1 都向右运动
C. m2 = 0.3 kg
D. 碰撞过程中系统损失了 0.4 J 的机械能
AC
课堂练习4
质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能是以下值吗?
(A)0.6v (B)0.4v (C)0.2v
解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:
B球速度的最大值发生在弹性碰撞时:
∵所以,只有0.4v是速度可能值
课堂练习5
1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
2. 非弹性碰撞:碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。
(1) 规律:动量守恒,机械能减少
(2) 能量转化情况:完全非弹性碰撞中系统动能损失最大
3. 对心碰撞和非对心碰撞
课堂总结
4.微观粒子的碰撞---散射
