第三章 3.1.1 空间向量及其加减﹑数乘运算
文档属性
| 名称 | 第三章 3.1.1 空间向量及其加减﹑数乘运算 |  | |
| 格式 | zip | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 15:15:38 | ||
图片预览








文档简介
(共22张PPT)
第三章
空间向量与立体几何
3.1 空间向量及其运算
3.1.1 空间向量及其加减﹑数乘运算
1.掌握空间向量相关的概念、几何表示法、字母表示法.
2.了解共线(平行)向量、共面向量的定义.
3.掌握空间向量的加减、数乘运算及运算律,共线向量、
共面向量的表示法.
4.理解共线、共面向量定理及其推论,并能利用它们证明
空间向量的共线、共面问题.
1.空间向量.
在空间,我们把具有________和________的量叫做空间向
量.向量的__________叫做向量的长度或模.
大小
方向
大小
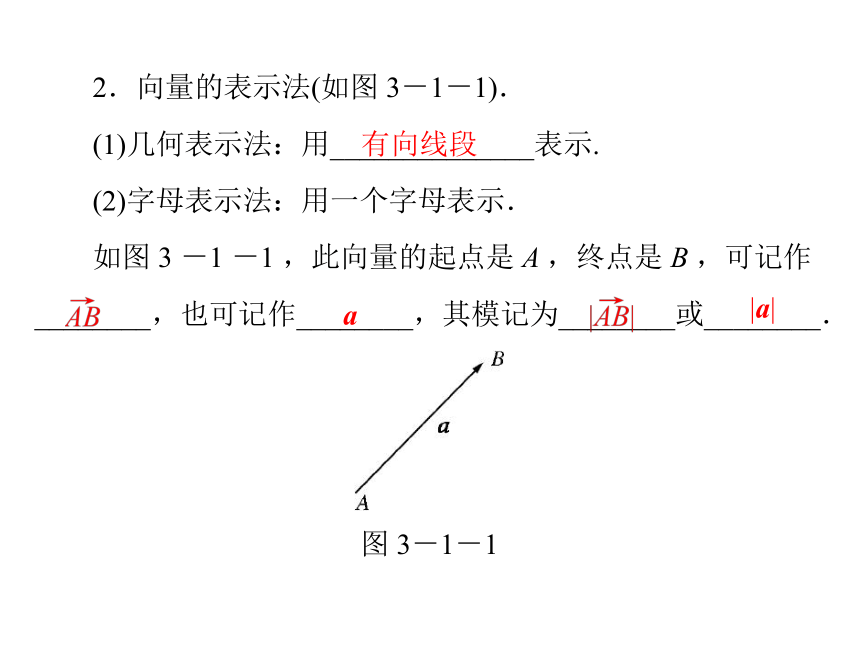
2.向量的表示法(如图 3-1-1).
(1)几何表示法:用______________表示.
(2)字母表示法:用一个字母表示.
如图 3 -1 -1 ,此向量的起点是 A ,终点是 B ,可记作
________,也可记作________,其模记为________或________.
图 3-1-1
有向线段
a
|a|
是________.当有向线段的起点A与终点B重合时,AB=0.
3.零向量.
长度为______的向量叫做零向量,记作 0,零向量的方向
→
4.单位向量.
模长为________的向量.
5.相反向量.
与向量 a 的______相等而__________相反的向量,称为 a
的相反向量,记作-a.
0
任意的
1
长度
方向
6.相等向量.
__________相同且________相等的向量称为相等向量.在
空间,同向且等长的有向线段表示同一向量或相等向量.
图 3-1-2
方向
模
OB=____________=__________;
CA=____________=__________.
7.类似于平面向量,定义空间向量的加减运算(如图
3-1-2).
→
→
a+b
a-b
8.空间向量的加法运算律.
(1)交换律:_________________.
(2)结合律:___________________.
9.向量的数乘.
实数λ与向量 a 的积仍然是一个向量,记作______,称为
向量的数乘.长度是_____________.当λ>0 时,λa 与向量
a的方向________;当λ<0 时,λa 与向量 a 的方向________;
当λ=0时,λa=________.
a+b=b+a
(a+b)+c=a+(b+c)
λa
|λ|·|a|
相同
相反
0
11.共线向量.
如果表示空间向量的有向线段所在的直线互相
________________,则这些向量叫做共线向量或__________.
12.共线向量定理.
对空间任意两个向量 a,b(b≠0),a∥b 的充要条件是存在
实数λ,使__________,称此为共线向量定理.
注意:b≠0 不可丢掉,否则实数λ就不一定存在.
(1)分配律:__________________.
(2)结合律:__________________.
10.数乘运算律.
λ(a+b)=λa+λb
λ(μa)=(λμ)a
平行或重合
平行向量
a=λb
13.共面向量.
________________________叫做共面向量.空间任意两个
向量______________.
14.共面向理定理.
如果两个向量 a,b 不共线,那么向量 p 与向量 a,b 共面
的充要条件是:_______________________________________.
称此为共面向量定理.
平行于同一平面的向量
总是共面的
存在唯一的有序实数对(x,y),使p=xa+yb
【要点1】正确理解空间向量的概念.
【剖析】(1)向量是既有大小又有方向的量,向量的模是正
数或 0,是可以进行比较大小的.由于方向不能比较大小,因
此“大于”、“小于”对向量来说是没有意义的,比如可以说|a|>|b|,
但不能说 a>b.
(2)在空间,单位向量、向量的模、相等的向量和相反向量
等概念与平面向量中相对应的概念完全一致.
【要点2】向量的三角形法则和平行四边形法则的要点是
什么?
【剖析】对于向量加法运用平行四边形法则要求两向量有
共同起点,运用三角形法则要求向量首尾顺次相连.对于向量
减法要求两向量有共同的起点.
【要点3】空间向量的数乘运算.
【剖析】空间向量数乘运算的结果仍是一个向量,可以根据
定义来判断它的方向和大小.向量 a 的模可以扩大(当|λ|>1时),
也可以缩小(当|λ|<1 时);向量 a 的方向可以不改变(当λ>0时),
也可以改变(当λ<0 时).实数与向量可以求积,但是不能进行
加减,例如λ+a,λ-a 是没有意义的.
【要点4】共线向量与共面向量.
【剖析】对于空间任意两个向量 a,b(b≠0),共线向量定
理可分解为以下两个命题:①a∥b 存在唯一实数λ使 a=λb;
②存在唯一实数λ,使得 a=λb a∥b.
对于空间任意两个向量,它们总是共面的,但空间任意三
个向量就不一定共面了.三个非零向量 a,b,c,其中任意两
个向量不共线,则它们共面的充要条件:存在三个非零实数 l,
m,n,使 la+mb+nc=0.
题型1 空间向量的线性运算
例1:如图 3-1-3,在正方体 ABCD-A1B1C1D1 中,下列
各式中运算的结果为向量 AC1 的共有(
)
A.1 个
C.3 个
B.2 个
D.4 个
图 3-1-3
思维突破:化简向量表达式主要是利用平行四边形法则或
三角形法则,遇到减法时既可以转化成加法,也可以按减法法
则进行运算.
答案:D
A
CD=7a-2b,则一定共线的三点是(
题型2 共线问题
→
)
A.A,B,D
C.B,C,D
B.A,B,C
D.A,C,D
思维突破:证明三点共线的关键是证明以某点为起点的两
个向量中,一个向量可以表示为另一个向量与某个实数的数乘
形式.
答案:A
(1)OB+OM=3OP-OA;
(2)OP=4OA-OB-OM.
题型3 共面问题
例3:对于平面 ABM 外的任一点 O,确定在下列条件下,
点 P 是否与点 A,B,M 一定共面?
→ → → →
→ → → →
思维突破:要证明四点共面,可以根据共面向量定理证明
其中任意两个点所构成的向量共面,从而得到四点共面.
【变式与拓展】
A.有相同起点的向量
C.共面向量
B.等长的向量
D.不共面向量
C
第三章
空间向量与立体几何
3.1 空间向量及其运算
3.1.1 空间向量及其加减﹑数乘运算
1.掌握空间向量相关的概念、几何表示法、字母表示法.
2.了解共线(平行)向量、共面向量的定义.
3.掌握空间向量的加减、数乘运算及运算律,共线向量、
共面向量的表示法.
4.理解共线、共面向量定理及其推论,并能利用它们证明
空间向量的共线、共面问题.
1.空间向量.
在空间,我们把具有________和________的量叫做空间向
量.向量的__________叫做向量的长度或模.
大小
方向
大小
2.向量的表示法(如图 3-1-1).
(1)几何表示法:用______________表示.
(2)字母表示法:用一个字母表示.
如图 3 -1 -1 ,此向量的起点是 A ,终点是 B ,可记作
________,也可记作________,其模记为________或________.
图 3-1-1
有向线段
a
|a|
是________.当有向线段的起点A与终点B重合时,AB=0.
3.零向量.
长度为______的向量叫做零向量,记作 0,零向量的方向
→
4.单位向量.
模长为________的向量.
5.相反向量.
与向量 a 的______相等而__________相反的向量,称为 a
的相反向量,记作-a.
0
任意的
1
长度
方向
6.相等向量.
__________相同且________相等的向量称为相等向量.在
空间,同向且等长的有向线段表示同一向量或相等向量.
图 3-1-2
方向
模
OB=____________=__________;
CA=____________=__________.
7.类似于平面向量,定义空间向量的加减运算(如图
3-1-2).
→
→
a+b
a-b
8.空间向量的加法运算律.
(1)交换律:_________________.
(2)结合律:___________________.
9.向量的数乘.
实数λ与向量 a 的积仍然是一个向量,记作______,称为
向量的数乘.长度是_____________.当λ>0 时,λa 与向量
a的方向________;当λ<0 时,λa 与向量 a 的方向________;
当λ=0时,λa=________.
a+b=b+a
(a+b)+c=a+(b+c)
λa
|λ|·|a|
相同
相反
0
11.共线向量.
如果表示空间向量的有向线段所在的直线互相
________________,则这些向量叫做共线向量或__________.
12.共线向量定理.
对空间任意两个向量 a,b(b≠0),a∥b 的充要条件是存在
实数λ,使__________,称此为共线向量定理.
注意:b≠0 不可丢掉,否则实数λ就不一定存在.
(1)分配律:__________________.
(2)结合律:__________________.
10.数乘运算律.
λ(a+b)=λa+λb
λ(μa)=(λμ)a
平行或重合
平行向量
a=λb
13.共面向量.
________________________叫做共面向量.空间任意两个
向量______________.
14.共面向理定理.
如果两个向量 a,b 不共线,那么向量 p 与向量 a,b 共面
的充要条件是:_______________________________________.
称此为共面向量定理.
平行于同一平面的向量
总是共面的
存在唯一的有序实数对(x,y),使p=xa+yb
【要点1】正确理解空间向量的概念.
【剖析】(1)向量是既有大小又有方向的量,向量的模是正
数或 0,是可以进行比较大小的.由于方向不能比较大小,因
此“大于”、“小于”对向量来说是没有意义的,比如可以说|a|>|b|,
但不能说 a>b.
(2)在空间,单位向量、向量的模、相等的向量和相反向量
等概念与平面向量中相对应的概念完全一致.
【要点2】向量的三角形法则和平行四边形法则的要点是
什么?
【剖析】对于向量加法运用平行四边形法则要求两向量有
共同起点,运用三角形法则要求向量首尾顺次相连.对于向量
减法要求两向量有共同的起点.
【要点3】空间向量的数乘运算.
【剖析】空间向量数乘运算的结果仍是一个向量,可以根据
定义来判断它的方向和大小.向量 a 的模可以扩大(当|λ|>1时),
也可以缩小(当|λ|<1 时);向量 a 的方向可以不改变(当λ>0时),
也可以改变(当λ<0 时).实数与向量可以求积,但是不能进行
加减,例如λ+a,λ-a 是没有意义的.
【要点4】共线向量与共面向量.
【剖析】对于空间任意两个向量 a,b(b≠0),共线向量定
理可分解为以下两个命题:①a∥b 存在唯一实数λ使 a=λb;
②存在唯一实数λ,使得 a=λb a∥b.
对于空间任意两个向量,它们总是共面的,但空间任意三
个向量就不一定共面了.三个非零向量 a,b,c,其中任意两
个向量不共线,则它们共面的充要条件:存在三个非零实数 l,
m,n,使 la+mb+nc=0.
题型1 空间向量的线性运算
例1:如图 3-1-3,在正方体 ABCD-A1B1C1D1 中,下列
各式中运算的结果为向量 AC1 的共有(
)
A.1 个
C.3 个
B.2 个
D.4 个
图 3-1-3
思维突破:化简向量表达式主要是利用平行四边形法则或
三角形法则,遇到减法时既可以转化成加法,也可以按减法法
则进行运算.
答案:D
A
CD=7a-2b,则一定共线的三点是(
题型2 共线问题
→
)
A.A,B,D
C.B,C,D
B.A,B,C
D.A,C,D
思维突破:证明三点共线的关键是证明以某点为起点的两
个向量中,一个向量可以表示为另一个向量与某个实数的数乘
形式.
答案:A
(1)OB+OM=3OP-OA;
(2)OP=4OA-OB-OM.
题型3 共面问题
例3:对于平面 ABM 外的任一点 O,确定在下列条件下,
点 P 是否与点 A,B,M 一定共面?
→ → → →
→ → → →
思维突破:要证明四点共面,可以根据共面向量定理证明
其中任意两个点所构成的向量共面,从而得到四点共面.
【变式与拓展】
A.有相同起点的向量
C.共面向量
B.等长的向量
D.不共面向量
C
