第三章 3.1.2 空间向量的数量积运算
文档属性
| 名称 | 第三章 3.1.2 空间向量的数量积运算 |  | |
| 格式 | zip | ||
| 文件大小 | 338.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 15:15:38 | ||
图片预览





文档简介
(共17张PPT)
3.1.2 空间向量的数量积运算
1.了解空间向量夹角的概念及表示方法.
2.掌握空间向量数量积的计算方法及应用.
3.能将立体几何问题转化为向量运算问题.
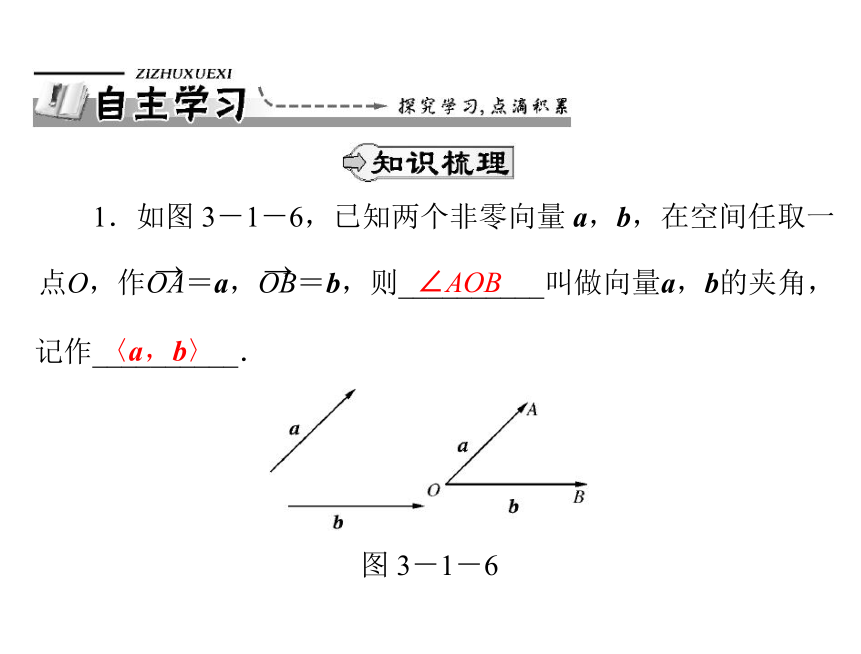
点O,作OA=a,OB=b,则__________叫做向量a,b的夹角,
1.如图 3-1-6,已知两个非零向量 a,b,在空间任取一
→ →
记作__________.
图 3-1-6
∠AOB
〈a,b〉
[0,π]
向量a,b互相垂直
a⊥b
a,b的数量积
a·b
a·b=|a||b|cos〈a,b〉
4.空间向量的数量积满足以下运算律:
(1)(λa)·b=__________.
(2)a·b=__________.
(3)a·(b+c)=______________.
注意:一般情况下(a·b)·c 与 a·(b·c)是不相等的.
5.线线垂直.
若 a,b 是非零向量,则 a⊥b __________.
λ(a·b)
b·a
a·b+a·c
a·b=0
【要点】利用数量积求夹角与长度.
(1)AB·AC;(2)AD·BD;(3)GF·AC.
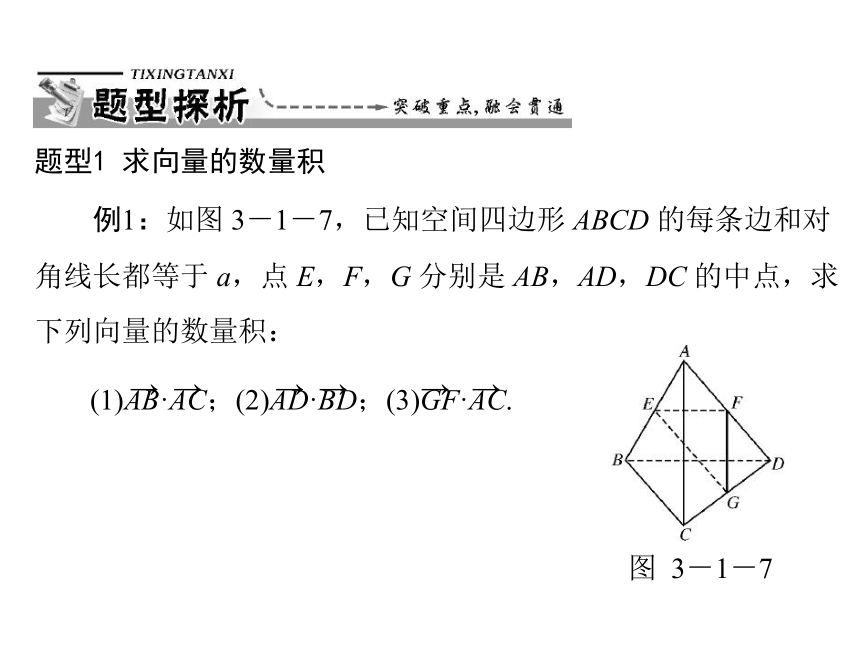
题型1 求向量的数量积
例1:如图 3-1-7,已知空间四边形 ABCD 的每条边和对
角线长都等于 a,点 E,F,G 分别是 AB,AD,DC 的中点,求
下列向量的数量积:
→ → → → → →
图 3-1-7
【变式与拓展】
则 a·b+b·c+c·a=(
)
A.1.5
B.-1.5
C.0.5
D.-0.5
C
PC的自身数量积,由已知向量的模及向量间的夹角,得其模的
题型2 求线段的长度
例2:已知在 ABCD 中,AD=4,CD=3,∠D=60°,
PA ⊥平面 ABCD,并且 PA =6,求 PC 的长.
思维突破:求 PC 的长,先把 PC 转化为向量,然后求向量
→
平方,再开方即为所求.
求|PC|.
【变式与拓展】
2.已知 PA ⊥平面 ABC,∠ABC=120°,PA=AB=BC=6,
→
题型3 向量的夹角问题
例3:如图3-1-8,在空间四边形 OABC 中,OA=8,AB=6,
AC=4,BC=5,∠OAC=45°,∠OAB=60°,求 OA与 BC 夹角
的余弦值.
图 3-1-8
【变式与拓展】
3.如图 3-1-9,在平行六面体 AC′中,∠B′BA=
∠B′BC=∠ABC=60°,AB=1,AD=2,AA′=3,求 A′D
与 D′C 所成的角的余弦值.
图 3-1-9
3.1.2 空间向量的数量积运算
1.了解空间向量夹角的概念及表示方法.
2.掌握空间向量数量积的计算方法及应用.
3.能将立体几何问题转化为向量运算问题.
点O,作OA=a,OB=b,则__________叫做向量a,b的夹角,
1.如图 3-1-6,已知两个非零向量 a,b,在空间任取一
→ →
记作__________.
图 3-1-6
∠AOB
〈a,b〉
[0,π]
向量a,b互相垂直
a⊥b
a,b的数量积
a·b
a·b=|a||b|cos〈a,b〉
4.空间向量的数量积满足以下运算律:
(1)(λa)·b=__________.
(2)a·b=__________.
(3)a·(b+c)=______________.
注意:一般情况下(a·b)·c 与 a·(b·c)是不相等的.
5.线线垂直.
若 a,b 是非零向量,则 a⊥b __________.
λ(a·b)
b·a
a·b+a·c
a·b=0
【要点】利用数量积求夹角与长度.
(1)AB·AC;(2)AD·BD;(3)GF·AC.
题型1 求向量的数量积
例1:如图 3-1-7,已知空间四边形 ABCD 的每条边和对
角线长都等于 a,点 E,F,G 分别是 AB,AD,DC 的中点,求
下列向量的数量积:
→ → → → → →
图 3-1-7
【变式与拓展】
则 a·b+b·c+c·a=(
)
A.1.5
B.-1.5
C.0.5
D.-0.5
C
PC的自身数量积,由已知向量的模及向量间的夹角,得其模的
题型2 求线段的长度
例2:已知在 ABCD 中,AD=4,CD=3,∠D=60°,
PA ⊥平面 ABCD,并且 PA =6,求 PC 的长.
思维突破:求 PC 的长,先把 PC 转化为向量,然后求向量
→
平方,再开方即为所求.
求|PC|.
【变式与拓展】
2.已知 PA ⊥平面 ABC,∠ABC=120°,PA=AB=BC=6,
→
题型3 向量的夹角问题
例3:如图3-1-8,在空间四边形 OABC 中,OA=8,AB=6,
AC=4,BC=5,∠OAC=45°,∠OAB=60°,求 OA与 BC 夹角
的余弦值.
图 3-1-8
【变式与拓展】
3.如图 3-1-9,在平行六面体 AC′中,∠B′BA=
∠B′BC=∠ABC=60°,AB=1,AD=2,AA′=3,求 A′D
与 D′C 所成的角的余弦值.
图 3-1-9
