第三章 3.1.3 空间向量运算的坐标表示
文档属性
| 名称 | 第三章 3.1.3 空间向量运算的坐标表示 |

|
|
| 格式 | zip | ||
| 文件大小 | 235.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 00:00:00 | ||
图片预览





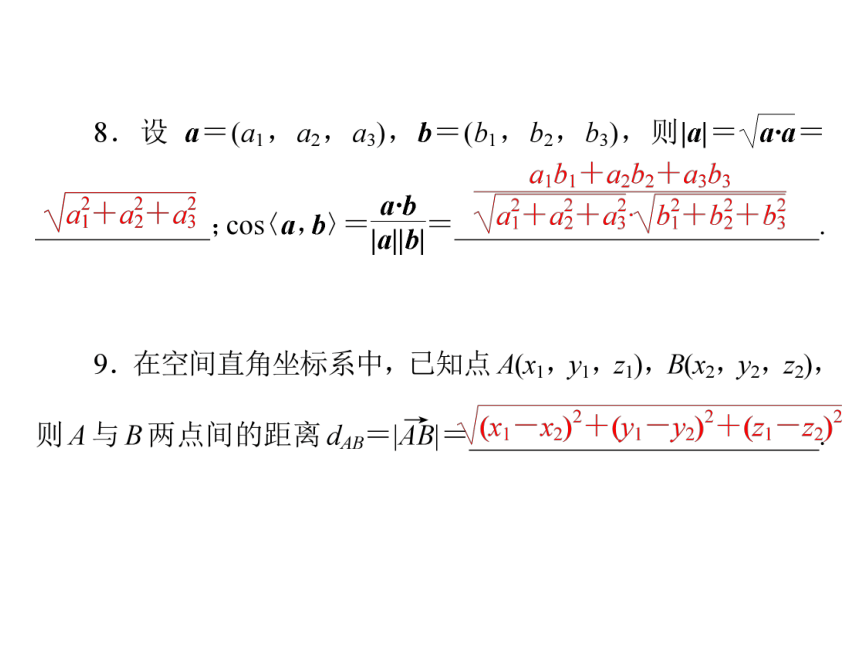

文档简介
(共16张PPT)
3.1.3 空间向量运算的坐标表示
1.了解空间向量基本定理、意义及其表示.
2.理解空间向量的正交分解、长度公式、夹角公式和空间
两点间距离公式.
3.掌握在简单问题中运用空间三个不共面的向量作为基底
表示其他向量.能用向量的坐标运算解决简单几何体中的问题.
1.设 i,j,k 是空间三个两两垂直的向量,那么对空间任
一向量 p,存在一个__________________,使得____________,
我们称____________为向量 p 在 i,j,k 上的分向量.
2.空间向量基本定理.
如果三个向量 a,b,c 不共面,那么对空间任一向量 p,
存在有序实数组(x,y,z),使得 p=____________.
有序实数组(x,y,z)
p=xi+yj+zk
xi,yj,zk
xa+yb+zc
3.如果三个向量 a,b,c 不共面,那么所有空间向量所组
成的集合就是{p|p=xa+yb+zc,x,y,z∈R}.这个集合可看
作是由 a,b,c 生成的,我们把____________叫做空间的一个
基底 ,_________ 都叫做基向量 .空间任何________________
都可构成空间的一个基底.
4.设 e1,e2,e3 为有公共起点 O 的三个两两相互垂直的单
位向量,称它们为________________.
{a,b,c}
a,b,c
三个不共面的向量
单位正交基底
5.在空间选定一个单位正交基底{e1,e2,e3 },以 e1,e2,e3
的公共起点 O 为______,分别以 e1,e2,e3 的方向为 x 轴, y 轴,
z 轴的_________建立空间直角坐标系 Oxyz.那么对于空间任意一个
向量 p ,一定可以把它平行移动,使它的起点________________,
得到一个向量________.由空间向量分解定理可知,存在有序实
数组{x,y,z},使得_________________.我们把_______称作向
量p 在单位正交基底 e1,e2,e3 下的坐标,记作____________.
原点
正方向
与原点O重合
p=xe1+ye2+ze3
x,y,z
p=(x,y,z)
6.一个向量在直角坐标系中的坐标等于表示这个向量的有
向线段的_____________________.
7.设 a=(a1,a2,a3),b=(b1,b2,b3),则
a+b=________________________;
a-b=________________________;
λa=__________________;a·b=________________;
a∥b ______________________________________;
a⊥b ____________________.
终点与始点的坐标之差
(a1+b1,a2+b2,a3+b3)
(a1-b1,a2-b2,a3-b3)
(λa1,λa2,λa3)
a1b1+a2b2+a3b3
a1=λb1,a2=λb2,a3=λb3(λ∈R)
a1b1+a2b2+a3b3=0
题型1 空间向量的坐标运算
例1:已知 a=(2,-1,-2),b=(0,-1,4),求 a+b;
a-b;a·b;(2a)·(-b);(a+b)·(a-b).
自主解答:a+b=(2+0,-1-1,-2+4)=(2,-2,2);
a-b=(2-0,-1+1,-2-4)=(2,0,-6);
a·b=2×0+(-1)×(-1)+(-2)×4=-7;
(2a)·(-b)=-2(a·b)=-2×(-7)=14;
(a+b)·(a-b)=2×2+(-2)×0+2×(-6)=-8.
思维突破:计算时注意运算法则和公式的灵活应用.
【变式与拓展】
1.已知向量 a=(3,-2,1),b=(-2,4,0),则 4a+2b=(
)
A.(16,0,4)
C.(8,16,4)
B.(8,-16,4)
D.(8,0,4)
解析:4a+2b=4(3,-2,1)+2(-2,4,0)=(12,-8,4)+ (-4,8,0)
=(8,0,4).故选 D.
D
并求MN,DC的坐标.
题型2 坐标表示空间向量
例2:已知 PA 垂直于边长为 1 的正方形 ABCD 所在的平面,
M,N 分别是 AB,PC 的中点,并且 PA =AD.建立直角坐标系
→ →
思维突破:空间直角坐标系建立的关键是寻找三条两两互
相垂直的直线.
【变式与拓展】
2.设{i,j,k}是空间向量的一个单位正交基底,a=3i+
2j-k,b=-2i+4j+2k,则向量 a,b 的坐标分别是__________,
____________.
(3,2,-1)
(-2,4,2)
(2)求cos〈BA1,CB1〉的值.
题型3 空间向量的夹角、距离公式的应用
例3:已知如图 3-1-10,在直三棱柱 ABC-A1B1C1 的底
面△ABC 中,CA=CB=1,∠BCA=90°,棱 AA1=2,点 N 是
A1A 的中点.
(1)求 BN 的长;
→ →
图 3-1-10
【变式与拓展】
3.已知 a=(1-t,1-t,t),b=(2,t,t),则|b-a|的最小值
是(
)
C
O 为坐标原点,求向量OA与OB的夹角.
4.已知点 A 的坐标是(-1,-2,6),点 B 的坐标是(1,2,-6),
→ →
3.1.3 空间向量运算的坐标表示
1.了解空间向量基本定理、意义及其表示.
2.理解空间向量的正交分解、长度公式、夹角公式和空间
两点间距离公式.
3.掌握在简单问题中运用空间三个不共面的向量作为基底
表示其他向量.能用向量的坐标运算解决简单几何体中的问题.
1.设 i,j,k 是空间三个两两垂直的向量,那么对空间任
一向量 p,存在一个__________________,使得____________,
我们称____________为向量 p 在 i,j,k 上的分向量.
2.空间向量基本定理.
如果三个向量 a,b,c 不共面,那么对空间任一向量 p,
存在有序实数组(x,y,z),使得 p=____________.
有序实数组(x,y,z)
p=xi+yj+zk
xi,yj,zk
xa+yb+zc
3.如果三个向量 a,b,c 不共面,那么所有空间向量所组
成的集合就是{p|p=xa+yb+zc,x,y,z∈R}.这个集合可看
作是由 a,b,c 生成的,我们把____________叫做空间的一个
基底 ,_________ 都叫做基向量 .空间任何________________
都可构成空间的一个基底.
4.设 e1,e2,e3 为有公共起点 O 的三个两两相互垂直的单
位向量,称它们为________________.
{a,b,c}
a,b,c
三个不共面的向量
单位正交基底
5.在空间选定一个单位正交基底{e1,e2,e3 },以 e1,e2,e3
的公共起点 O 为______,分别以 e1,e2,e3 的方向为 x 轴, y 轴,
z 轴的_________建立空间直角坐标系 Oxyz.那么对于空间任意一个
向量 p ,一定可以把它平行移动,使它的起点________________,
得到一个向量________.由空间向量分解定理可知,存在有序实
数组{x,y,z},使得_________________.我们把_______称作向
量p 在单位正交基底 e1,e2,e3 下的坐标,记作____________.
原点
正方向
与原点O重合
p=xe1+ye2+ze3
x,y,z
p=(x,y,z)
6.一个向量在直角坐标系中的坐标等于表示这个向量的有
向线段的_____________________.
7.设 a=(a1,a2,a3),b=(b1,b2,b3),则
a+b=________________________;
a-b=________________________;
λa=__________________;a·b=________________;
a∥b ______________________________________;
a⊥b ____________________.
终点与始点的坐标之差
(a1+b1,a2+b2,a3+b3)
(a1-b1,a2-b2,a3-b3)
(λa1,λa2,λa3)
a1b1+a2b2+a3b3
a1=λb1,a2=λb2,a3=λb3(λ∈R)
a1b1+a2b2+a3b3=0
题型1 空间向量的坐标运算
例1:已知 a=(2,-1,-2),b=(0,-1,4),求 a+b;
a-b;a·b;(2a)·(-b);(a+b)·(a-b).
自主解答:a+b=(2+0,-1-1,-2+4)=(2,-2,2);
a-b=(2-0,-1+1,-2-4)=(2,0,-6);
a·b=2×0+(-1)×(-1)+(-2)×4=-7;
(2a)·(-b)=-2(a·b)=-2×(-7)=14;
(a+b)·(a-b)=2×2+(-2)×0+2×(-6)=-8.
思维突破:计算时注意运算法则和公式的灵活应用.
【变式与拓展】
1.已知向量 a=(3,-2,1),b=(-2,4,0),则 4a+2b=(
)
A.(16,0,4)
C.(8,16,4)
B.(8,-16,4)
D.(8,0,4)
解析:4a+2b=4(3,-2,1)+2(-2,4,0)=(12,-8,4)+ (-4,8,0)
=(8,0,4).故选 D.
D
并求MN,DC的坐标.
题型2 坐标表示空间向量
例2:已知 PA 垂直于边长为 1 的正方形 ABCD 所在的平面,
M,N 分别是 AB,PC 的中点,并且 PA =AD.建立直角坐标系
→ →
思维突破:空间直角坐标系建立的关键是寻找三条两两互
相垂直的直线.
【变式与拓展】
2.设{i,j,k}是空间向量的一个单位正交基底,a=3i+
2j-k,b=-2i+4j+2k,则向量 a,b 的坐标分别是__________,
____________.
(3,2,-1)
(-2,4,2)
(2)求cos〈BA1,CB1〉的值.
题型3 空间向量的夹角、距离公式的应用
例3:已知如图 3-1-10,在直三棱柱 ABC-A1B1C1 的底
面△ABC 中,CA=CB=1,∠BCA=90°,棱 AA1=2,点 N 是
A1A 的中点.
(1)求 BN 的长;
→ →
图 3-1-10
【变式与拓展】
3.已知 a=(1-t,1-t,t),b=(2,t,t),则|b-a|的最小值
是(
)
C
O 为坐标原点,求向量OA与OB的夹角.
4.已知点 A 的坐标是(-1,-2,6),点 B 的坐标是(1,2,-6),
→ →
