第一章 1.2.1 充分条件与必要条件
文档属性
| 名称 | 第一章 1.2.1 充分条件与必要条件 |  | |
| 格式 | zip | ||
| 文件大小 | 129.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 15:15:38 | ||
图片预览




文档简介
(共10张PPT)
1.2.1
充分条件与必要条件
1.理解充分条件、必要条件的意义.
2.能进行有关充分、必要条件的判断.
p 的__________条件.
1.一般地,“若 p,则 q”为真命题,是指由 p 通过推理
可以得出 q.这时,我们就说,由 p 可推出 q,记作 p q,并且
说 p 是 q 的__________条件,q 是 p 的__________条件.
2.若 p q,但 q p,则称 p 是 q 的__________ 条件,q是
/
充分
必要
充分不必要
必要不充分
【要点1】命题“若 p,则 q”与“p 是 q 的充分条件”有何关
系,其逆命题与“p 是 q 的必要条件”有何关系.
【剖析】对“若 p,则 q”形式的命题,若此命题为真命题,
则 p q,故 p 是 q 的充分条件;反之,若 p 是 q 的充分条件,
则命题“若 p,则 q”是真命题.同理若其逆命题成立,则 p 是
q 的必要条件;反之,若 p 是 q 的必要条件,则命题“若 p,则
q”的逆命题是真命题.
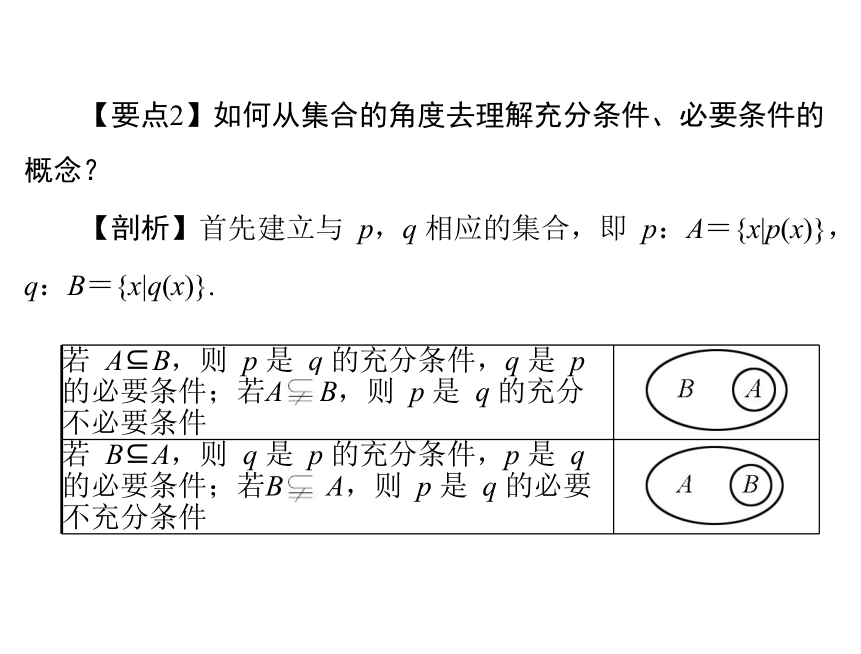
若 A B,则 p 是 q 的充分条件,q 是 p 的必要条件;若A B,则 p 是 q 的充分不必要条件
若 B A,则 q 是 p 的充分条件,p 是 q 的必要条件;若B A,则 p 是 q 的必要不充分条件
【要点2】如何从集合的角度去理解充分条件、必要条件的
概念?
【剖析】首先建立与 p,q 相应的集合,即 p:A={x|p(x)},
q:B={x|q(x)}.
题型1 充分条件与必要条件的判断
例1:下列形如“若 p,则 q”的命题是否是真命题?它的
逆命题是真命题吗?p 是 q 的什么条件?
(1)若直线 a 与平面α的一条直线垂直,则 a⊥α;
(2)若两直线平行,则它们的斜率相等;
(3)若数列的通项公式为 an=n,则它的前 3 项为 a1=1,
a2=2,a3=3.
思维突破:判断 p 是 q 的什么条件的方法:①验证由 p 能
否推出 q,由 q 能否推出 p;②利用原命题、逆命题的真假来
判断 p 是 q 的什么条件.
自主解答:(1)原命题是假命题,逆命题是真命题,故 p 是
q 的必要但不充分条件.
(2)原命题和逆命题都是假命题,故 p 是 q 的既不充分也不
必要条件.
(3)原命题是真命题,逆命题是假命题,故 p 是 q 的充分但
不必要条件.
【变式与拓展】
1.(2012 年安徽)设平面α与平面β相交于直线 m,直线 a
在平面α内,直线 b 在平面β内,且 b⊥m,则“α⊥β”是“a⊥b”
的(
)
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
题型2 充分条件与必要条件的应用
例2:不等式(a+x)(1+x)<0 成立的一个充分不必要条件是
-2)
A.a≤-2 B.a≥2
C.a<-2 D.a>2
思维突破:若命题可以用集合表示,则将其用集合表示出
来,然后再用集合的观点探究充分条件和必要条件.
答案:D
D.x≤- 或 x≥3
【变式与拓展】
2.不等式 2x2 -5x-3≥0 成立的一个充分不必要条件是
(
)
C
B.x≥0
A.x<0
C.x∈{-1,3,5}
1
2
1.2.1
充分条件与必要条件
1.理解充分条件、必要条件的意义.
2.能进行有关充分、必要条件的判断.
p 的__________条件.
1.一般地,“若 p,则 q”为真命题,是指由 p 通过推理
可以得出 q.这时,我们就说,由 p 可推出 q,记作 p q,并且
说 p 是 q 的__________条件,q 是 p 的__________条件.
2.若 p q,但 q p,则称 p 是 q 的__________ 条件,q是
/
充分
必要
充分不必要
必要不充分
【要点1】命题“若 p,则 q”与“p 是 q 的充分条件”有何关
系,其逆命题与“p 是 q 的必要条件”有何关系.
【剖析】对“若 p,则 q”形式的命题,若此命题为真命题,
则 p q,故 p 是 q 的充分条件;反之,若 p 是 q 的充分条件,
则命题“若 p,则 q”是真命题.同理若其逆命题成立,则 p 是
q 的必要条件;反之,若 p 是 q 的必要条件,则命题“若 p,则
q”的逆命题是真命题.
若 A B,则 p 是 q 的充分条件,q 是 p 的必要条件;若A B,则 p 是 q 的充分不必要条件
若 B A,则 q 是 p 的充分条件,p 是 q 的必要条件;若B A,则 p 是 q 的必要不充分条件
【要点2】如何从集合的角度去理解充分条件、必要条件的
概念?
【剖析】首先建立与 p,q 相应的集合,即 p:A={x|p(x)},
q:B={x|q(x)}.
题型1 充分条件与必要条件的判断
例1:下列形如“若 p,则 q”的命题是否是真命题?它的
逆命题是真命题吗?p 是 q 的什么条件?
(1)若直线 a 与平面α的一条直线垂直,则 a⊥α;
(2)若两直线平行,则它们的斜率相等;
(3)若数列的通项公式为 an=n,则它的前 3 项为 a1=1,
a2=2,a3=3.
思维突破:判断 p 是 q 的什么条件的方法:①验证由 p 能
否推出 q,由 q 能否推出 p;②利用原命题、逆命题的真假来
判断 p 是 q 的什么条件.
自主解答:(1)原命题是假命题,逆命题是真命题,故 p 是
q 的必要但不充分条件.
(2)原命题和逆命题都是假命题,故 p 是 q 的既不充分也不
必要条件.
(3)原命题是真命题,逆命题是假命题,故 p 是 q 的充分但
不必要条件.
【变式与拓展】
1.(2012 年安徽)设平面α与平面β相交于直线 m,直线 a
在平面α内,直线 b 在平面β内,且 b⊥m,则“α⊥β”是“a⊥b”
的(
)
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
题型2 充分条件与必要条件的应用
例2:不等式(a+x)(1+x)<0 成立的一个充分不必要条件是
-2
A.a≤-2 B.a≥2
C.a<-2 D.a>2
思维突破:若命题可以用集合表示,则将其用集合表示出
来,然后再用集合的观点探究充分条件和必要条件.
答案:D
D.x≤- 或 x≥3
【变式与拓展】
2.不等式 2x2 -5x-3≥0 成立的一个充分不必要条件是
(
)
C
B.x≥0
A.x<0
C.x∈{-1,3,5}
1
2
