第二章 2.3.1 双曲线及其标准方程
文档属性
| 名称 | 第二章 2.3.1 双曲线及其标准方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 234.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
2.3 双曲线
2.3.1
双曲线及其标准方程
1.了解双曲线标准方程的推导过程.
2.能根据条件熟练求出双曲线的标准方程.
3.掌握双曲线的定义与标准方程.
1.双曲线的定义.
平面内到两定点 F1,F2 的距离的差的___________________
____________________的点的轨迹叫做双曲线.这两个定点叫
做双曲线的________,
两焦点之间的距离叫做双曲线的________.
绝对值是常数
(小于|F1F2|且大于0)
焦点
焦距
2.双曲线的标准方程.
(1)焦点在 x 轴上,标准方程为______________________,
焦点坐标为______________,a,b,c 的关系是____________.
(2)焦点在 y 轴上,标准方程为________________________,
焦点坐标为______________,a,b,c 的关系是____________.
(c,0),(-c,0)
c2=a2+b2
(0,c),(0,-c)
c2=a2+b2
【要点1】如何理解双曲线的定义?
【剖析】“常数要小于|F1F2|且大于 0” 这一条件可以用
“三角形的两边之差小于第三边”加以理解.“差的绝对值”这一
条件是因为当|MF1|<|MF2|或|MF1|>|MF2|时,点 P 的轨迹为
双曲线的一支.而双曲线是由两个分支组成的,故在定义中
应为“差的绝对值”.
①当||PF1|-|PF2||=0 时,点 P 的轨迹是线段 F1F2 的垂直平
分线;
②当 0<||PF1|-|PF2||=2a<|F1F2|时,点 P 的轨迹是双曲线;
③当|PF1|-|PF2|=2a 或|PF1|-|PF2|=-2a 时,点 P 的轨迹
只是双曲线的其中一支;
④当||PF1|-|PF2||=2a=|F1F2|时,点 P 的轨迹是以 F1,F2
为端点向外的两条射线;
⑤当||PF1|-|PF2||=2a>|F1F2|时,点 P 的轨迹不存在.
【要点2】双曲线的定义中“差的绝对值”中的“绝对值”能
否去掉?
【剖析】不能去掉,若去掉绝对值,点的轨迹就成为双曲
线的一支.
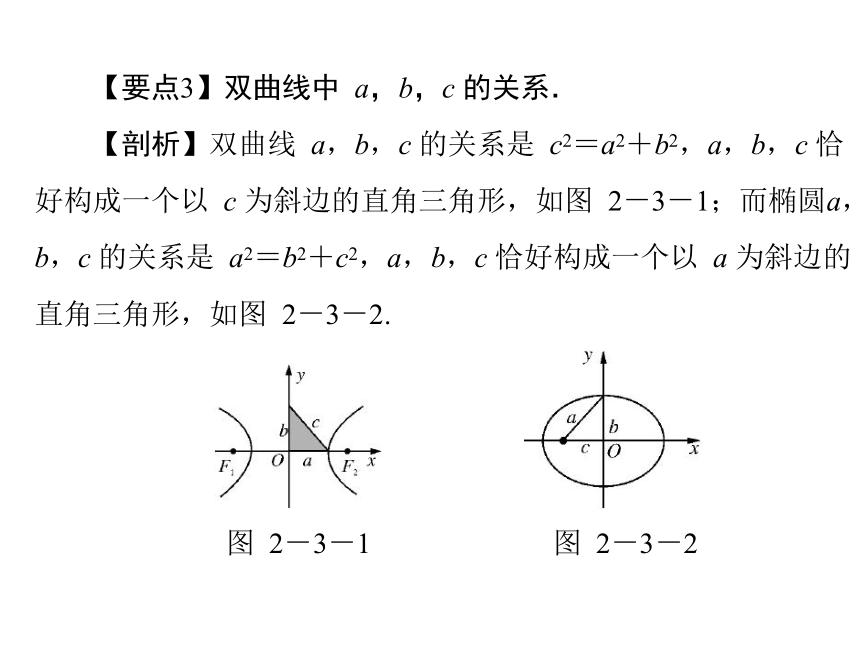
【要点3】双曲线中 a,b,c 的关系.
【剖析】双曲线 a,b,c 的关系是 c2=a2+b2,a,b,c 恰
好构成一个以 c 为斜边的直角三角形,如图 2-3-1;而椭圆a,
b,c 的关系是 a2=b2+c2,a,b,c 恰好构成一个以 a 为斜边的
直角三角形,如图 2-3-2.
图 2-3-1
图 2-3-2
题型 1 双曲线定义及应用
例1:AB 是某平面上一定线段且|AB|=3,点 P 是该平面内
)
A.圆
B.双曲线的一支
C.椭圆的一部分
D.抛物线
答案:B
【变式与拓展】
1.“ab<0”是方程 ax2+by2=1 表示双曲线的(
)条件.
C
A.必要不充分
B.充分不必要
C.充要
D.既不充分也不必要
题型2 求双曲线的标准方程
例2:已知双曲线两个焦点的坐标为 F1(-13,0),F2(13,0),
双曲线上一点 P 到 F1,F2 的距离的差的绝对值等于 10,求双曲
线的标准方程.
思维突破:求解双曲线的标准方程,只要确定焦点所在坐标
轴及 a,b的值即可,通常由定义可以确定2a,根据c2=a2 +b2,
基本量 a,b,c 中知道其中两个,可求出第三个.
【变式与拓展】
2.若双曲线的一个顶点坐标为(3,0),焦距为 10,则它的
标准方程为________________.
题型 3 含有参数的双曲线方程
是(
)
A.k<2 或 k>5 B.2C.k>5 或-25 或 k>2
思维突破:根据双曲线的标准方程可知,需要(|k|-2)·(4-
k)<0,联立不等式组求得 k 的范围.
答案:C
+
【变式与拓展】
4.如果方程
x2 y2
m+1 m+2
=1 表示双曲线,那么 m 的取值
范围是__________.
-2
2.3 双曲线
2.3.1
双曲线及其标准方程
1.了解双曲线标准方程的推导过程.
2.能根据条件熟练求出双曲线的标准方程.
3.掌握双曲线的定义与标准方程.
1.双曲线的定义.
平面内到两定点 F1,F2 的距离的差的___________________
____________________的点的轨迹叫做双曲线.这两个定点叫
做双曲线的________,
两焦点之间的距离叫做双曲线的________.
绝对值是常数
(小于|F1F2|且大于0)
焦点
焦距
2.双曲线的标准方程.
(1)焦点在 x 轴上,标准方程为______________________,
焦点坐标为______________,a,b,c 的关系是____________.
(2)焦点在 y 轴上,标准方程为________________________,
焦点坐标为______________,a,b,c 的关系是____________.
(c,0),(-c,0)
c2=a2+b2
(0,c),(0,-c)
c2=a2+b2
【要点1】如何理解双曲线的定义?
【剖析】“常数要小于|F1F2|且大于 0” 这一条件可以用
“三角形的两边之差小于第三边”加以理解.“差的绝对值”这一
条件是因为当|MF1|<|MF2|或|MF1|>|MF2|时,点 P 的轨迹为
双曲线的一支.而双曲线是由两个分支组成的,故在定义中
应为“差的绝对值”.
①当||PF1|-|PF2||=0 时,点 P 的轨迹是线段 F1F2 的垂直平
分线;
②当 0<||PF1|-|PF2||=2a<|F1F2|时,点 P 的轨迹是双曲线;
③当|PF1|-|PF2|=2a 或|PF1|-|PF2|=-2a 时,点 P 的轨迹
只是双曲线的其中一支;
④当||PF1|-|PF2||=2a=|F1F2|时,点 P 的轨迹是以 F1,F2
为端点向外的两条射线;
⑤当||PF1|-|PF2||=2a>|F1F2|时,点 P 的轨迹不存在.
【要点2】双曲线的定义中“差的绝对值”中的“绝对值”能
否去掉?
【剖析】不能去掉,若去掉绝对值,点的轨迹就成为双曲
线的一支.
【要点3】双曲线中 a,b,c 的关系.
【剖析】双曲线 a,b,c 的关系是 c2=a2+b2,a,b,c 恰
好构成一个以 c 为斜边的直角三角形,如图 2-3-1;而椭圆a,
b,c 的关系是 a2=b2+c2,a,b,c 恰好构成一个以 a 为斜边的
直角三角形,如图 2-3-2.
图 2-3-1
图 2-3-2
题型 1 双曲线定义及应用
例1:AB 是某平面上一定线段且|AB|=3,点 P 是该平面内
)
A.圆
B.双曲线的一支
C.椭圆的一部分
D.抛物线
答案:B
【变式与拓展】
1.“ab<0”是方程 ax2+by2=1 表示双曲线的(
)条件.
C
A.必要不充分
B.充分不必要
C.充要
D.既不充分也不必要
题型2 求双曲线的标准方程
例2:已知双曲线两个焦点的坐标为 F1(-13,0),F2(13,0),
双曲线上一点 P 到 F1,F2 的距离的差的绝对值等于 10,求双曲
线的标准方程.
思维突破:求解双曲线的标准方程,只要确定焦点所在坐标
轴及 a,b的值即可,通常由定义可以确定2a,根据c2=a2 +b2,
基本量 a,b,c 中知道其中两个,可求出第三个.
【变式与拓展】
2.若双曲线的一个顶点坐标为(3,0),焦距为 10,则它的
标准方程为________________.
题型 3 含有参数的双曲线方程
是(
)
A.k<2 或 k>5 B.2
思维突破:根据双曲线的标准方程可知,需要(|k|-2)·(4-
k)<0,联立不等式组求得 k 的范围.
答案:C
+
【变式与拓展】
4.如果方程
x2 y2
m+1 m+2
=1 表示双曲线,那么 m 的取值
范围是__________.
-2
