第二章 2.3.2 双曲线的简单几何性质
文档属性
| 名称 | 第二章 2.3.2 双曲线的简单几何性质 |  | |
| 格式 | zip | ||
| 文件大小 | 335.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 15:15:38 | ||
图片预览






文档简介
(共16张PPT)
2.3.2 双曲线的简单几何性质
1.了解双曲线的简单几何性质(范围、对称性、顶点、实
轴长和虚轴长等).
2.理解离心率的定义、取值范围和渐近线方程.
3.掌握标准方程中 a,b,c,e 间的关系.
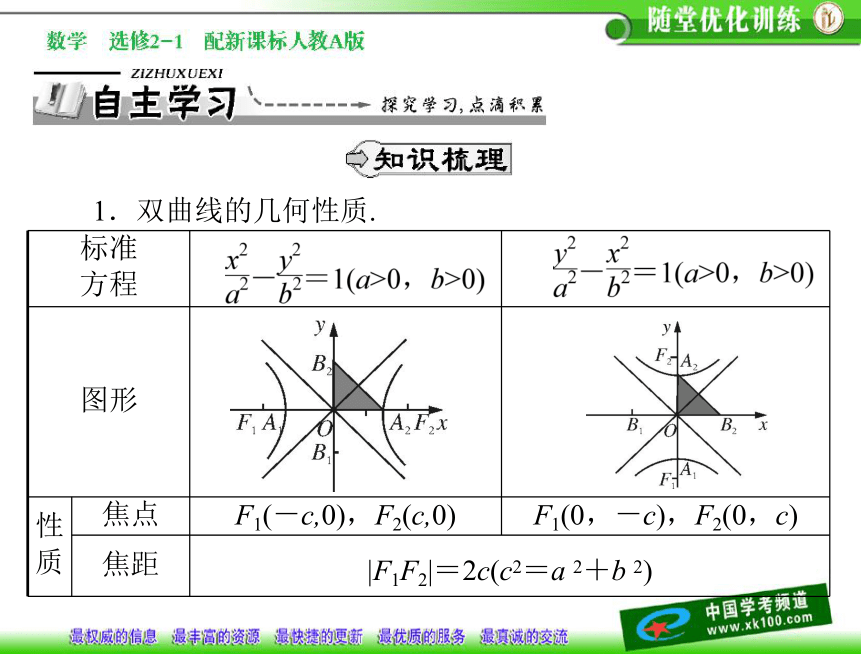
标准
方程
图形
性
质 焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距
|F1F2|=2c(c2=a 2+b 2)
1.双曲线的几何性质.
标准
方程
性
质 范围 |x|≥____,y∈R |y|≥______,x∈R
对称 关于 x 轴、y 轴成轴对称,关于原点成中心对称
顶点 (-a,0),(a,0) (0,-a),(0,a)
轴 实轴长 2a,虚轴长 2b
离心率
渐近线
续表
a
a
实轴和虚轴
y=±x
双曲线
双曲线的准线
【要点1】椭圆与双曲线几何性质的比较.
【剖析】(1)双曲线只有两个顶点,而椭圆有四个顶点,这
与椭圆不同.不能把双曲线的虚轴与椭圆的短轴混淆.
(2)椭圆的焦点总在长轴上,双曲线的焦点总在实轴上.
(3)椭圆离心率越大(即越接近于 1),椭圆就越扁平;而双曲
线的离心率越大,双曲线的形状从扁狭逐渐变得开阔,就是说
双曲线的“张口”逐渐增大.
【要点2】双曲线有两个顶点?双曲线的焦点能在虚轴上吗?
【剖析】两个.不能,焦点只能在实轴上.
题型1 双曲线的几何性质
例1:求双曲线 9y2-16x2=144 的半实轴长、半虚轴上、
焦点坐标、离心率和渐近线方程.
【变式与拓展】
1.双曲线
y2
20
-
x2
16
=-1 的实轴长为________,虚轴长为
______________ ,焦点坐标为______________ ,顶点坐标为
______________,离心率 e=______,渐近线方程为_________.
8
(-6,0),(6,0)
(-4,0),(4,0)
题型2 利用几何性质求标准方程
思维突破:双曲线焦点可能在 x 轴上,也可能在 y 轴上.
解答时要分两类情况.
【变式与拓展】
C
题型3 求双曲线的离心率
C
2.3.2 双曲线的简单几何性质
1.了解双曲线的简单几何性质(范围、对称性、顶点、实
轴长和虚轴长等).
2.理解离心率的定义、取值范围和渐近线方程.
3.掌握标准方程中 a,b,c,e 间的关系.
标准
方程
图形
性
质 焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距
|F1F2|=2c(c2=a 2+b 2)
1.双曲线的几何性质.
标准
方程
性
质 范围 |x|≥____,y∈R |y|≥______,x∈R
对称 关于 x 轴、y 轴成轴对称,关于原点成中心对称
顶点 (-a,0),(a,0) (0,-a),(0,a)
轴 实轴长 2a,虚轴长 2b
离心率
渐近线
续表
a
a
实轴和虚轴
y=±x
双曲线
双曲线的准线
【要点1】椭圆与双曲线几何性质的比较.
【剖析】(1)双曲线只有两个顶点,而椭圆有四个顶点,这
与椭圆不同.不能把双曲线的虚轴与椭圆的短轴混淆.
(2)椭圆的焦点总在长轴上,双曲线的焦点总在实轴上.
(3)椭圆离心率越大(即越接近于 1),椭圆就越扁平;而双曲
线的离心率越大,双曲线的形状从扁狭逐渐变得开阔,就是说
双曲线的“张口”逐渐增大.
【要点2】双曲线有两个顶点?双曲线的焦点能在虚轴上吗?
【剖析】两个.不能,焦点只能在实轴上.
题型1 双曲线的几何性质
例1:求双曲线 9y2-16x2=144 的半实轴长、半虚轴上、
焦点坐标、离心率和渐近线方程.
【变式与拓展】
1.双曲线
y2
20
-
x2
16
=-1 的实轴长为________,虚轴长为
______________ ,焦点坐标为______________ ,顶点坐标为
______________,离心率 e=______,渐近线方程为_________.
8
(-6,0),(6,0)
(-4,0),(4,0)
题型2 利用几何性质求标准方程
思维突破:双曲线焦点可能在 x 轴上,也可能在 y 轴上.
解答时要分两类情况.
【变式与拓展】
C
题型3 求双曲线的离心率
C
