第二章 2.4.2 抛物线的简单几何性质
文档属性
| 名称 | 第二章 2.4.2 抛物线的简单几何性质 |  | |
| 格式 | zip | ||
| 文件大小 | 258.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 15:15:38 | ||
图片预览






文档简介
(共14张PPT)
2.4.2 抛物线的简单几何性质
1.理解抛物线的几何性质(包括范围、对称性、顶点和离
心率).
2.能根据抛物线的几何性质对抛物线方程进行讨论,在此
基础上,列表、描点和画抛物线图形.
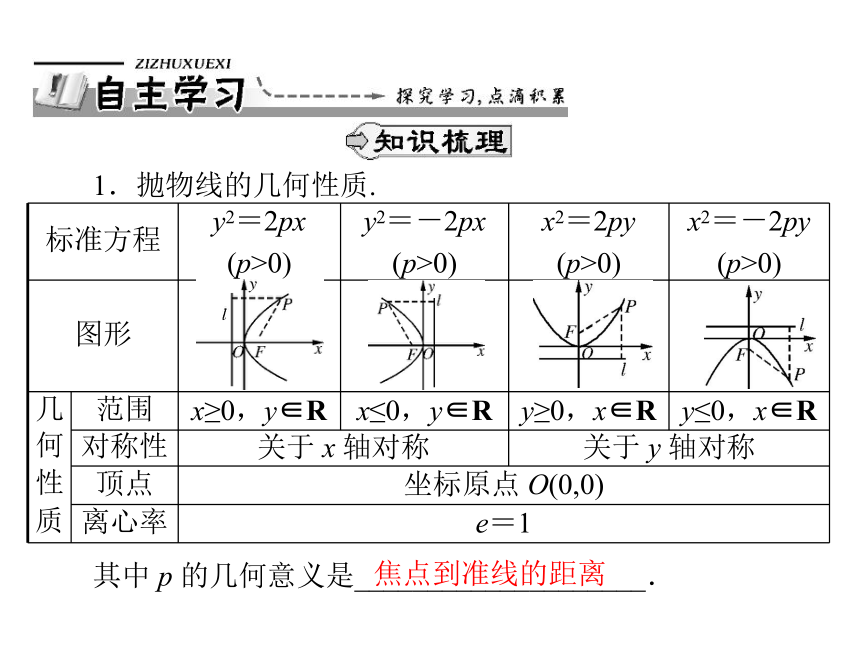
标准方程 y2=2px
(p>0) y2=-2px
(p>0) x2=2py
(p>0) x2=-2py
(p>0)
图形
几
何
性
质 范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
对称性 关于 x 轴对称 关于 y 轴对称
顶点 坐标原点 O(0,0)
离心率 e=1
1.抛物线的几何性质.
其中 p 的几何意义是____________________.
焦点到准线的距离
【要点】有人说抛物线类似于双曲线的一支,是这样吗?
抛物线与椭圆、双曲线有什么不同?
【剖析】不能把抛物线看作双曲线的一支,双曲线有渐近
线,而抛物线没有.直线与抛物线相交时,只要直线不平行于
抛物线的对称轴就一定有两个交点;而对于直线与双曲线的一
支相交来说,则要看直线与渐近线相交的情况才能确定交点个
数.当抛物线上的点趋向于无穷远时,过抛物线上的点的切线
行于抛物线的轴,即曲线接近于和轴平行,而双曲线上
的点趋于无穷时,它的切线的斜率接近于渐近线的斜率.
抛物线的性质和椭圆、双曲线比较起来,差别较大.它的
离心率等于 1;它只有一个焦点、一个顶点、一条对称轴和一
条准线,它无中心,也没有渐近线.
题型1 焦点弦问题
例1:已知直线 l 过抛物线 y2=2px(p>0)的焦点且与抛物线
相交,其中一点为(2p,2p),求其焦点弦的长度.
思维突破:①联立直线与抛物线方程,由根与系数关系求
得 x1+x2;②利用焦点弦公式.
【变式与拓展】
6
题型2 抛物线的对称性
例2:正三角形的一个顶点位于原点,另外两个顶点在抛
物线 y2=4x 上,求这个正三角形的边长.
【变式与拓展】
2.己知等边三角形的一个顶点是抛物线 y2=x 的焦点,另外
两个顶点在抛物线上,则这个等边三角形的边长为____________.
解析:利用抛物线的对称性,分两种情况讨论.
题型3 由几何性质求抛物线方程
例3:已知抛物线的顶点是坐标原点,对称轴为 x 轴,且
思维突破:圆和抛物线都关于 x 轴对称,所以它们的交点
也关于 x 轴对称,即公共弦被 x 轴垂直平分,于是由弦长可知
交点纵坐标.
【变式与拓展】
3.已知抛物线的焦点在 x 轴上,直线 y=2x-4 被抛物线
截得的线段长为 3
,则抛物线的标准方程是______________
________________.
y2=4x
或y2=-36x
2.4.2 抛物线的简单几何性质
1.理解抛物线的几何性质(包括范围、对称性、顶点和离
心率).
2.能根据抛物线的几何性质对抛物线方程进行讨论,在此
基础上,列表、描点和画抛物线图形.
标准方程 y2=2px
(p>0) y2=-2px
(p>0) x2=2py
(p>0) x2=-2py
(p>0)
图形
几
何
性
质 范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
对称性 关于 x 轴对称 关于 y 轴对称
顶点 坐标原点 O(0,0)
离心率 e=1
1.抛物线的几何性质.
其中 p 的几何意义是____________________.
焦点到准线的距离
【要点】有人说抛物线类似于双曲线的一支,是这样吗?
抛物线与椭圆、双曲线有什么不同?
【剖析】不能把抛物线看作双曲线的一支,双曲线有渐近
线,而抛物线没有.直线与抛物线相交时,只要直线不平行于
抛物线的对称轴就一定有两个交点;而对于直线与双曲线的一
支相交来说,则要看直线与渐近线相交的情况才能确定交点个
数.当抛物线上的点趋向于无穷远时,过抛物线上的点的切线
行于抛物线的轴,即曲线接近于和轴平行,而双曲线上
的点趋于无穷时,它的切线的斜率接近于渐近线的斜率.
抛物线的性质和椭圆、双曲线比较起来,差别较大.它的
离心率等于 1;它只有一个焦点、一个顶点、一条对称轴和一
条准线,它无中心,也没有渐近线.
题型1 焦点弦问题
例1:已知直线 l 过抛物线 y2=2px(p>0)的焦点且与抛物线
相交,其中一点为(2p,2p),求其焦点弦的长度.
思维突破:①联立直线与抛物线方程,由根与系数关系求
得 x1+x2;②利用焦点弦公式.
【变式与拓展】
6
题型2 抛物线的对称性
例2:正三角形的一个顶点位于原点,另外两个顶点在抛
物线 y2=4x 上,求这个正三角形的边长.
【变式与拓展】
2.己知等边三角形的一个顶点是抛物线 y2=x 的焦点,另外
两个顶点在抛物线上,则这个等边三角形的边长为____________.
解析:利用抛物线的对称性,分两种情况讨论.
题型3 由几何性质求抛物线方程
例3:已知抛物线的顶点是坐标原点,对称轴为 x 轴,且
思维突破:圆和抛物线都关于 x 轴对称,所以它们的交点
也关于 x 轴对称,即公共弦被 x 轴垂直平分,于是由弦长可知
交点纵坐标.
【变式与拓展】
3.已知抛物线的焦点在 x 轴上,直线 y=2x-4 被抛物线
截得的线段长为 3
,则抛物线的标准方程是______________
________________.
y2=4x
或y2=-36x
