第二章 2.4.3 抛物线习题课
文档属性
| 名称 | 第二章 2.4.3 抛物线习题课 |

|
|
| 格式 | zip | ||
| 文件大小 | 290.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
2.4.3 抛物线习题课
1.掌握直线与抛物线位置关系的判断.
2.掌握直线与抛物线相交时与弦长相关的知识.
3.掌握直线与抛物线相关的求值、证明问题.
1.在有关抛物线的问题中,如果要建立平面直角坐标系,
一般以______________为坐标轴的原点,以________________
为 x 轴或 y 轴,这样得到的抛物线方程就是标准方程.
2.直线与抛物线的位置关系有三种:相交、相切和相离.
(1)当直线与抛物线相交时,有______个公共点.
(2)当直线与抛物线相切时,有______公共点.
(3)当直线与抛物线相离时,有______个公共点.
抛物线的顶点
抛物线的对称轴
1或2
1
0
【要点1】如何处理直线与抛物线相交问题?
【剖析】直线与抛物线相交,涉及弦长问题,常用两点间
的距离公式计算弦长(即应用弦长公式);涉及弦长的中点问题,
常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标
联系起来.所谓“点差法”是指:设两个交点分别为 A(x1, y1),
B(x2,y2),然后代入抛物线方程中,得到两个式子,将两
式相减,再运用平方差公式,结合中点公式、斜率公式求解.
做题时,应充分挖掘题目中的隐含条件,寻找量与量之间的关
系将其灵活转化,往往能达到事半功倍的效果.
【要点2】怎样解决与曲线有关的最值问题?
【剖析】与曲线有关的最值问题,解法常有两种:当题目
的条件和结论能明显体现几何特征及意义,可考虑利用数形结
合法解;当题目的条件和结论能体现一种明确的函数关系,则
可先建立目标函数,再求这个函数的最值.
题型1 抛物线的应用
例1:一辆卡车高 3 米,宽 1.6 米,欲通过抛物线形隧道,
拱口宽恰好是抛物线的通径长,若拱口宽为 a 米,求能使卡车
通过的 a 的最小整数值.
思维突破:深刻理解题意,将实际问题与数学模型联系起
来,并建立恰当的坐标系,是解这类问题的关键.
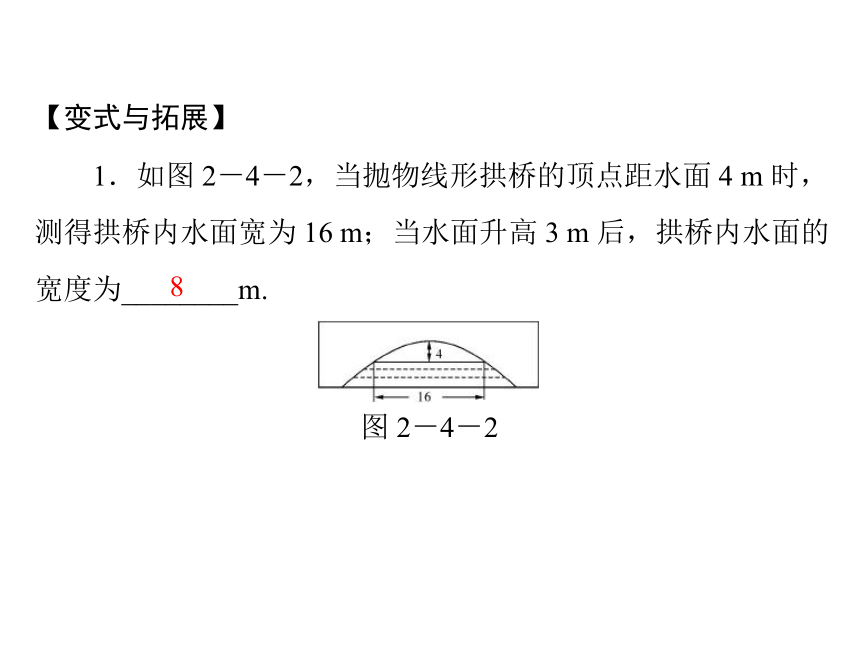
【变式与拓展】
1.如图 2-4-2,当抛物线形拱桥的顶点距水面 4 m 时,
测得拱桥内水面宽为 16 m;当水面升高 3 m 后,拱桥内水面的
宽度为________m.
图 2-4-2
8
题型2 直线与抛物线的位置关系
例2:设直线 y=2x+b 与抛物线 y2=4x 交于 A,B 两点,
思维突破:在解决弦长问题时,应注意充分利用已知条件,
由于弦在直线与抛物线相交时才存在,故应注意Δ>0 这一隐含
条件.
【变式与拓展】
题型3 抛物线的综合应用问题
【变式与拓展】
(1)求点 P 的轨迹 C 的方程;
(2)已知点 A(m,2)在曲线 C 上,过点 A 作曲线 C 的两条弦
AD 和 AE,且 AD⊥AE,判断:直线 DE 是否过定点?试证明
你的结论.
化简,得 t2-6t+5=4m2+8m,
即 t2-6t+9=4m2+8m+4,即(t-3)2=4(m+1)2.
∴t-3=±2(m+1),
∴t=2m+5 或 t=-2m+1,代入(*)式检验只有 t=2m+5
满足Δ>0.
∴直线 DE 的方程为 x=m(y+2)+5.
∴直线 DE 过定点(5,-2).
2.4.3 抛物线习题课
1.掌握直线与抛物线位置关系的判断.
2.掌握直线与抛物线相交时与弦长相关的知识.
3.掌握直线与抛物线相关的求值、证明问题.
1.在有关抛物线的问题中,如果要建立平面直角坐标系,
一般以______________为坐标轴的原点,以________________
为 x 轴或 y 轴,这样得到的抛物线方程就是标准方程.
2.直线与抛物线的位置关系有三种:相交、相切和相离.
(1)当直线与抛物线相交时,有______个公共点.
(2)当直线与抛物线相切时,有______公共点.
(3)当直线与抛物线相离时,有______个公共点.
抛物线的顶点
抛物线的对称轴
1或2
1
0
【要点1】如何处理直线与抛物线相交问题?
【剖析】直线与抛物线相交,涉及弦长问题,常用两点间
的距离公式计算弦长(即应用弦长公式);涉及弦长的中点问题,
常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标
联系起来.所谓“点差法”是指:设两个交点分别为 A(x1, y1),
B(x2,y2),然后代入抛物线方程中,得到两个式子,将两
式相减,再运用平方差公式,结合中点公式、斜率公式求解.
做题时,应充分挖掘题目中的隐含条件,寻找量与量之间的关
系将其灵活转化,往往能达到事半功倍的效果.
【要点2】怎样解决与曲线有关的最值问题?
【剖析】与曲线有关的最值问题,解法常有两种:当题目
的条件和结论能明显体现几何特征及意义,可考虑利用数形结
合法解;当题目的条件和结论能体现一种明确的函数关系,则
可先建立目标函数,再求这个函数的最值.
题型1 抛物线的应用
例1:一辆卡车高 3 米,宽 1.6 米,欲通过抛物线形隧道,
拱口宽恰好是抛物线的通径长,若拱口宽为 a 米,求能使卡车
通过的 a 的最小整数值.
思维突破:深刻理解题意,将实际问题与数学模型联系起
来,并建立恰当的坐标系,是解这类问题的关键.
【变式与拓展】
1.如图 2-4-2,当抛物线形拱桥的顶点距水面 4 m 时,
测得拱桥内水面宽为 16 m;当水面升高 3 m 后,拱桥内水面的
宽度为________m.
图 2-4-2
8
题型2 直线与抛物线的位置关系
例2:设直线 y=2x+b 与抛物线 y2=4x 交于 A,B 两点,
思维突破:在解决弦长问题时,应注意充分利用已知条件,
由于弦在直线与抛物线相交时才存在,故应注意Δ>0 这一隐含
条件.
【变式与拓展】
题型3 抛物线的综合应用问题
【变式与拓展】
(1)求点 P 的轨迹 C 的方程;
(2)已知点 A(m,2)在曲线 C 上,过点 A 作曲线 C 的两条弦
AD 和 AE,且 AD⊥AE,判断:直线 DE 是否过定点?试证明
你的结论.
化简,得 t2-6t+5=4m2+8m,
即 t2-6t+9=4m2+8m+4,即(t-3)2=4(m+1)2.
∴t-3=±2(m+1),
∴t=2m+5 或 t=-2m+1,代入(*)式检验只有 t=2m+5
满足Δ>0.
∴直线 DE 的方程为 x=m(y+2)+5.
∴直线 DE 过定点(5,-2).
