机械振动
图片预览




文档简介
(共63张PPT)
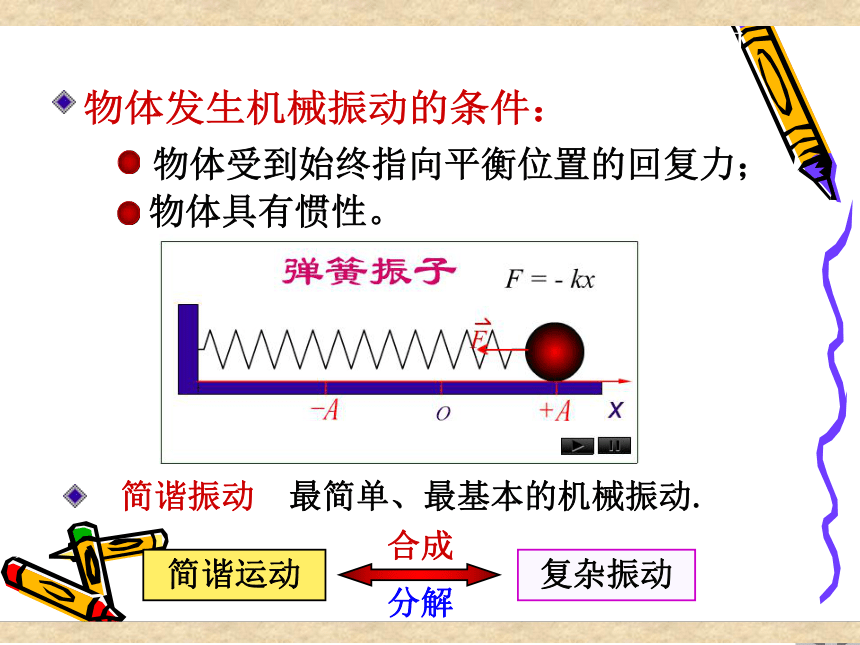
简谐振动
任一物理量在某一定值附近往复变化均称为振动.
运动形式: 直线、平面和空间振动.
例如一切发声体、心脏、海浪起伏、地震以及晶体
中原子的振动等.
简谐振动
简谐振动 最简单、最基本的机械振动.
简谐运动
复杂振动
合成
分解
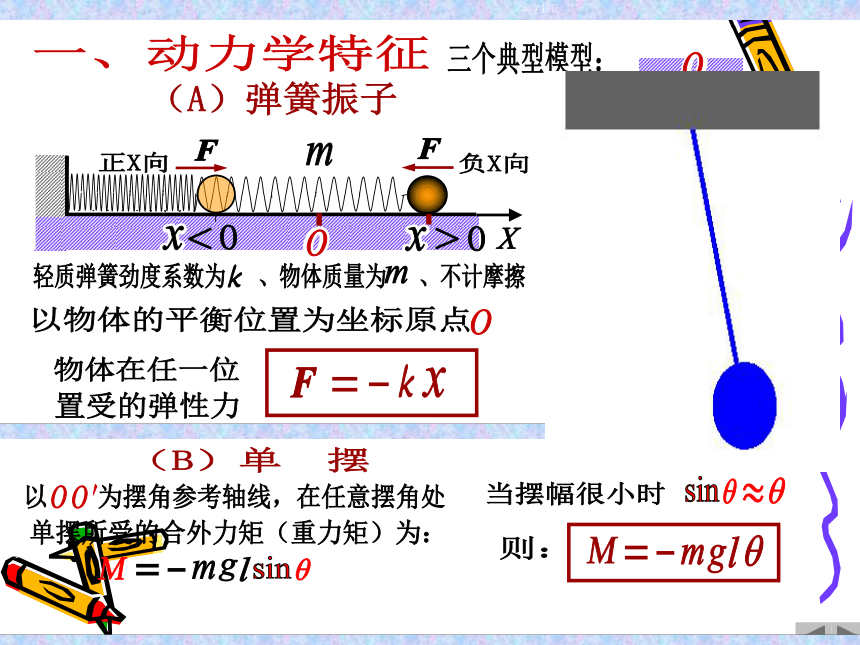
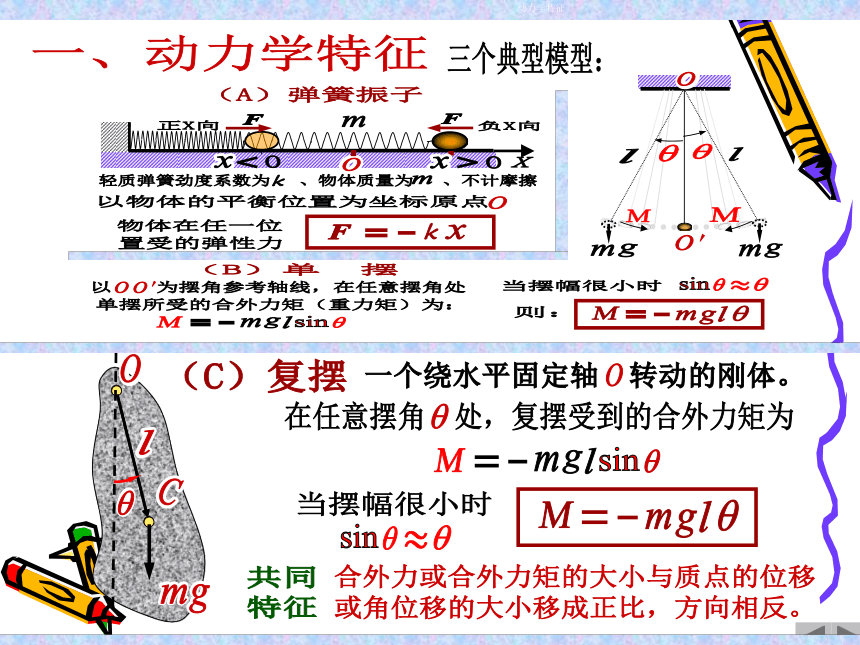
4-1 简谐振动的动力学特征
简谐振动:一个作往复运动的物体,如果其偏离平衡位置的位移x(或角位移 )随时间t按余弦(或正弦)规律变化的振动。
谐振子: 作简谐振动的物体.
简谐振动(simple harmonic vibration)
是研究各种复杂振动的重要基础。
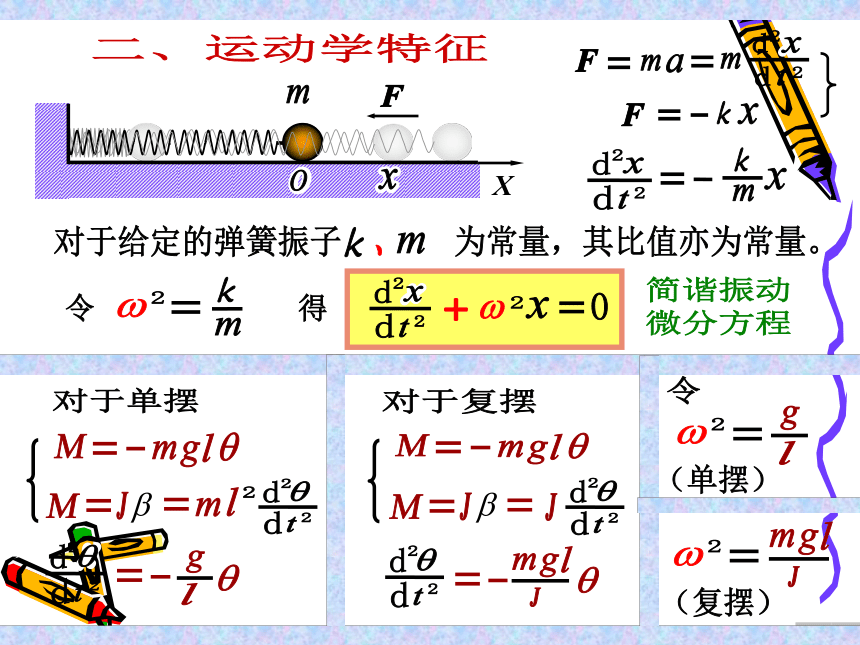
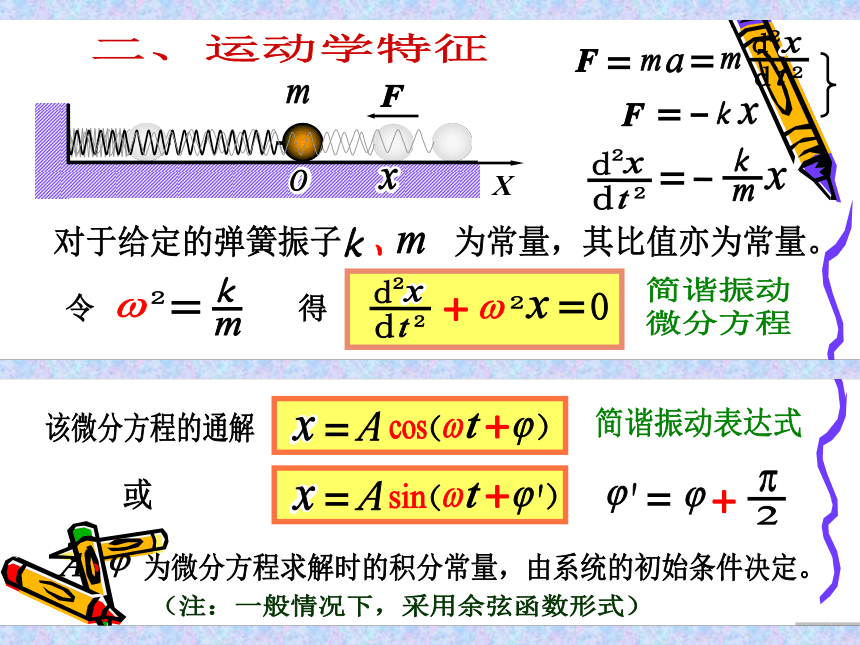
动学特征
动力学特征
运动学特征
X
X
续
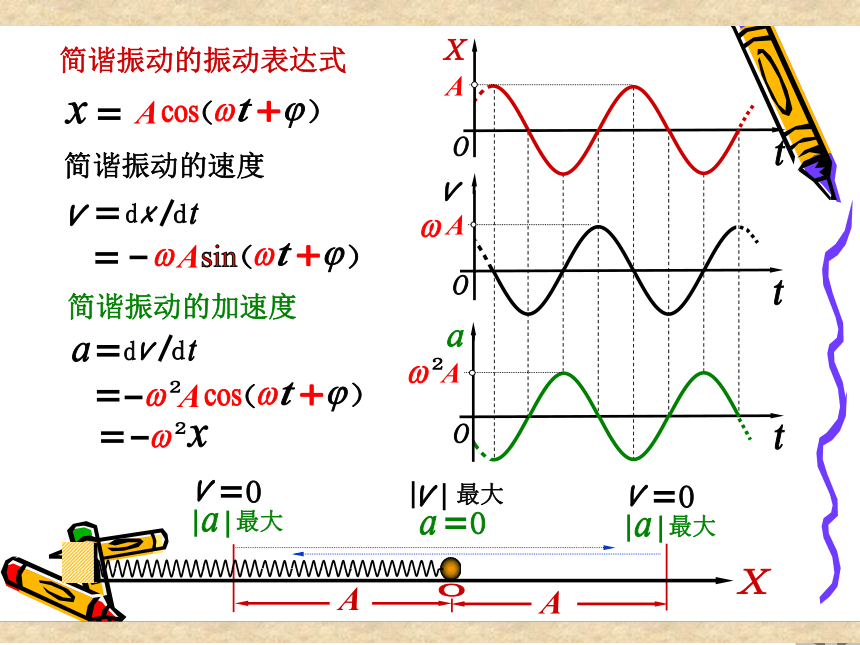
简谐振动的加速度
A
A
简谐振动的振动表达式
简谐振动的速度
A
A
A
最大
最大
最大
A
A
A
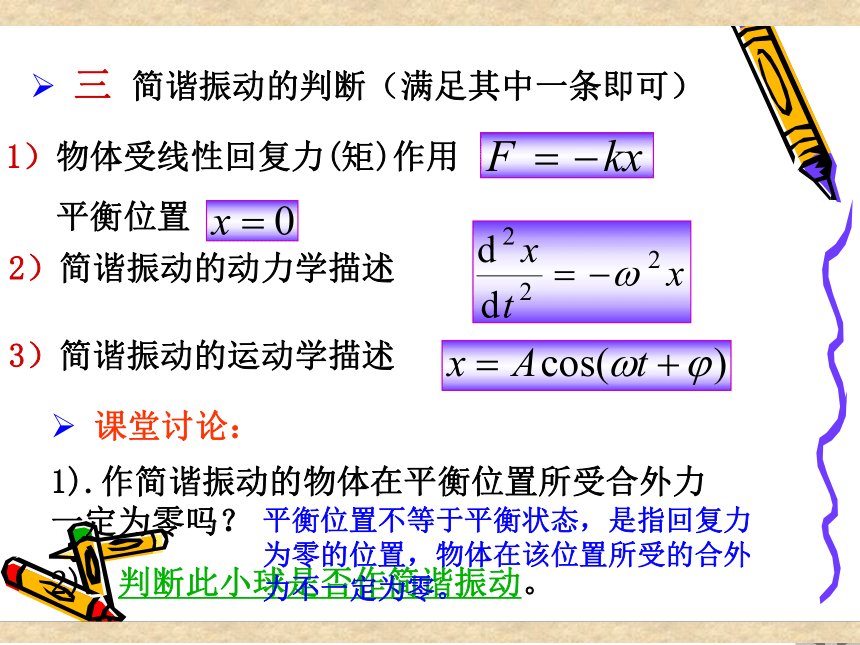
三 简谐振动的判断(满足其中一条即可)
2)简谐振动的动力学描述
3)简谐振动的运动学描述
课堂讨论:
1).作简谐振动的物体在平衡位置所受合外力 一定为零吗?
2). 判断此小球是否作简谐振动。
1)物体受线性回复力(矩)作用
平衡位置
平衡位置不等于平衡状态,是指回复力为零的位置,物体在该位置所受的合外力不一定为零。
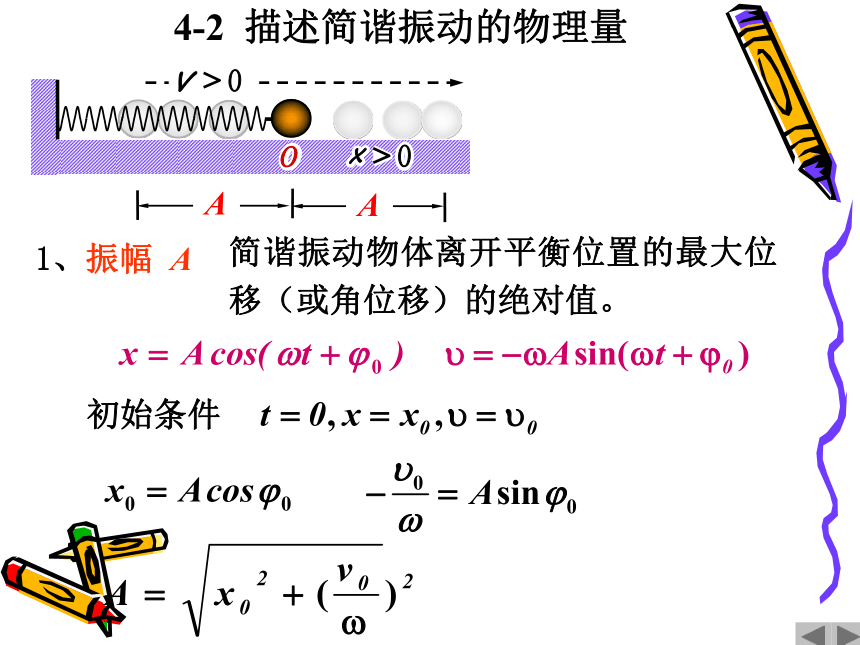
1、振幅 A
简谐振动物体离开平衡位置的最大位移(或角位移)的绝对值。
初始条件
4-2 描述简谐振动的物理量
A
A
频率 :单位时间内全振动的次数。
2、周期 、频率、角频率
对弹簧振子
角频率
固有周期、固有频率、固有角频率
周期T :物体完成一次全振动所需时间。
单摆
复摆
0 是t =0时刻的位相—初相位
3、相位和初相位
—相位,决定简谐振动物体的运动状态
4. 相位差
=( 2 t+ 2)-( 1 t+ 1)
对两同频率的谐振动 = 2- 1
初相差
同相和反相
t
x
o
A1
-A1
A2
- A2
x1
x2
T
同相
当 =2k ,k=0,±1,±2…,两振动步调相同,称同相
x2
T
x
o
A1
-A1
A2
- A2
x1
t
反相
当 =(2k+1) , k=0,±1,±2... 两振动步调相反,称反相
2 超前于 1 或 1滞后于 2
相位差反映了两个振动不同程度的参差错落
例1:一弹簧振子系统,弹簧的劲度系数为k=0.72N/m,物体的质量为m=20g。今将物体从平衡位置沿桌面向右拉长到0.04m处,由静止释放,求振动方程。
又因为x0为正,初速度v0=0,可得
因而简谐振动的方程为:
解:设 ,只要确定A、ω和 0即可。由题可知,k=0.72N/m,m=20g=0.02kg,x0=0.04m,v0=0,代入公式可得
R
M
m
k
O
X
x
旋转矢量法
A
A
X
X
O
j
M ( 0 )
A
j
初相
M ( t )
t
w
t
w
M ( t )
t
w
M ( t )
t
w
M ( t )
M ( t )
t
w
M ( t )
t
w
M (T )
T
w
周期 T
M ( t )
t
w
M ( t )
t
w
X
O
j
M ( 0 )
j
初相
M ( t )
t
w
A
循环往复
4-3 简谐振动的旋转矢量表示法
旋转
矢量 的
端点在
轴上的投
影点的运
动为简谐
运动.
x
0
t+ 0
O
p
t=0
M
说明:
旋转矢量法是研究简谐振动的一种直观方法;
不能把M的运动误认为简谐振动。
模 振幅A
作坐标轴ox ,自原点作一矢量
与x 轴的夹角 相位
角速度 角频率
初始与x 轴的夹角 初相
旋转矢量 简谐振动
(旋转矢量旋转一周所需的时间)
用旋转矢量图画简谐运动的 图
P点坐标、速度和加速度都作简谐振动
矢端M在x 轴投影的运动规律:
P点的坐标
即M点位矢在x 轴上的投影
速度
即M点速率在x 轴上的投影
加速度
即M点向心加速度在x 轴上的投影
0
t+ 0
O
p
t=0
M
用旋转矢量表示相位关系
同相
反相
谐振动的位移、速度、加速度之间的位相关系
t
o
T
a
v
x
T/4
T/4
由图可见:
x
t+
o
·
例. 已知简谐振动 , 当 时位
移为 且向 负向运动。
求(1)振动方 程。
(2) 且向 正向运动时的速度、加速
度及从这一位置回到平衡位置的最小时间。
解(1)
由旋转矢量 得
(2)先求 由旋转矢量法
(半个周期)
o
由旋转矢量法
(用解析法也可求出!)
例. 已知 x t 曲线,写出振动方程,
并求它们的位相差?
x
解:
或
或
位相差反映了两振动达到同一状态有时间差
讨论:
例 已知某简谐振动的 速度与时间的关系曲线如图所示,试求其振动方程。
解:方法1
设振动方程为
故振动方程为
方法2:
用旋转矢量法辅助求解。
v的旋转矢量与v轴夹角表示t 时刻相位
由图知
以弹簧振子为例
谐振动系统的能量=系统的动能Ek+系统的势能Ep
某一时刻,谐振子速度为v,位移为x
谐振动的动能和势能是时间的周期性函数
4-4 简谐振动的能量
动能
势能
情况同动能。
机械能
简谐振动系统机械能守恒
例七
该摆动系统的机械能守恒数学表达式
该摆的运动学微分方程及摆动周期
动能 刚体(直棒)转动动能
势能 系统的重力势能
以垂态直棒中心点 C 为重力零势点
令
机械能
机械能守恒,即 为恒量,
即
得 简谐角振动微分方程
该摆的振动周期
匀质细直悬棒
质量 m、长 L
在铅直面内摆动
摆幅很小
转动惯量
4-5 简谐振动的合成
某质点同时参与两个同频率且在同一条直线上的简谐运动
合振动
1、应用解析法
令
一、两个同方向同频率简谐运动的合成
2、应用旋转矢量法
x
y
合成振动
是简谐运动
3、讨论
合振幅最大
情况1
当 称为干涉相长
情况2
合振幅最小
当 称为干涉相消
情况3:一般情况
质点同时参与两个不同频率但在同一条直线上的简谐振动
合振动
假设
1
o
x
2
二、同方向不同频率的简谐振动的合成
合成振动表达式:
合振动是振幅按 |2A0cos2π(ν2-ν1)t/2| 缓慢变化的频率为(ν2+ν1)/2 的“准周期运动”
x
t
x2
t
x1
t
1 )单位时间内振动加强或减弱的次数叫拍频
2)合振动的“频率”为
其振幅变化的周期是由振幅绝对值变化来决定,即振动忽强忽弱。这种合振动忽强忽弱的现象称为拍。
拍现象的应用:
用标准音叉振动校准乐器
测定超声波
测定无线电频率
调制高频振荡的振幅和频率等
385 Hz
383 Hz
听到的音频
384 Hz
强度节拍性变化
2 Hz
四、两个相互垂直的同频率简谐振动的合成
某质点同时参与两个同频率的互相垂直方向的简谐运动
合振动的轨迹方程为
是个椭圆方程,具体形状由相位差决定。
讨论1
合振动的轨迹是一条通过原点的直线
讨论2
合振动的轨迹是一条通过原点的直线
讨论3
合振动的轨迹是椭圆方程,且顺时针旋转
讨论4
合振动的轨迹是椭圆方程,且逆时针旋转
讨论5
合振动的轨迹是的圆
讨论6
则为任一椭圆方程
综上所述:两个频率相同的互相垂直的简谐振动合成后,合振动在一直线上或者在椭圆上进行当两个分振动的振幅相等时,椭圆轨道就成为圆。
续上
或
为任意值时,合振动的轨迹一般为椭圆
五、两个垂直方向不同频率简谐运动的合成
合成运动不是周期性的运动。下面就两种情况讨论
视为同频率的合成:两个振动的相位差缓慢地变化,质点运动的轨道循环变化。
情况1:两个分振动的频率相差很小
合成运动的轨道是封闭曲线,运动也具有周期。这种运动轨迹的图形称为李萨如图形。
情况2:两个分振动的频率相差较大,有简单整数比关系
例如
由切点数之比
可测频率。
例4 有两个振动方向相同的简谐振动,其振动方程分别为 ,
1) 求它们的合振动方程;
问: 当 3为何值时, x1+x3的振动为最大值?当 3为何值时, x1+x3的振动为最小值?
解:1) 两个振动方向相同, 频率相同的简谐振动合成后还是简谐振动, 合振动方程为
2) 另有一同方向的简谐振动
所求的振动方程为
2)
当 时,相位相同。
当 时,相位相反。
根据已知条件,t=0时,合矢量应在第二象限,故
一、 阻尼振动
阻尼振动
能量随时间减小的振动称阻尼振动或减幅振动。
摩擦阻尼:
系统克服阻力作功使振幅受到摩擦力的作用,系统的动能转化为热能。
辐射阻尼:
振动以波的形式向外传波,使振动能量向周围辐射出去。
4-5 阻尼振动 受迫振动 共振
阻尼振动的振动方程(系统受到弱介质阻力而衰减)
振子动力学方程
振子受阻力
系统固有角频率
阻尼系数
弱介质阻力是指振子运动速度较低时,
介质对物体的阻力仅与速度的一次方成正比
—阻力系数
弱阻尼
弱阻尼
每一周期内损失的能量越小,振幅衰减越慢,周期越接近于谐振动。
阻尼振动的振幅按指数衰减
阻尼振动的准周期
临界阻尼
临界阻尼
系统不作往复运动,而是较快地回到平衡位置并停下来
过阻尼
过阻尼
系统不作往复运动,而是非常缓慢地回到平衡位置
二、 受迫振动
受迫振动 振动系统在周期性外力作用下的振动。
弱阻尼谐振子系统在策动力作用下的受迫振动的方程
令
周期性外力——策动力
稳定解
(1)频率: 等于策动力的频率
(2)振幅:
(3)初相:
特点:稳态时的受迫振动按简谐振动的规律变化
阻尼振动
简谐振动
三、共振
在一定条件下, 振幅出现极大值, 振动剧烈的现象。
1、位移共振
(1)共振频率 :
(2)共振振幅 :
2、速度共振
一定条件下, 速度振幅极大的现象。
速度共振时,速度与策动力同相,一周期内策动力总作正功,此时向系统输入的能量最大。
共振现象的危害
1940 年11月7日美国 Tocama 悬索桥因共振而坍塌
简谐振动
任一物理量在某一定值附近往复变化均称为振动.
运动形式: 直线、平面和空间振动.
例如一切发声体、心脏、海浪起伏、地震以及晶体
中原子的振动等.
简谐振动
简谐振动 最简单、最基本的机械振动.
简谐运动
复杂振动
合成
分解
4-1 简谐振动的动力学特征
简谐振动:一个作往复运动的物体,如果其偏离平衡位置的位移x(或角位移 )随时间t按余弦(或正弦)规律变化的振动。
谐振子: 作简谐振动的物体.
简谐振动(simple harmonic vibration)
是研究各种复杂振动的重要基础。
动学特征
动力学特征
运动学特征
X
X
续
简谐振动的加速度
A
A
简谐振动的振动表达式
简谐振动的速度
A
A
A
最大
最大
最大
A
A
A
三 简谐振动的判断(满足其中一条即可)
2)简谐振动的动力学描述
3)简谐振动的运动学描述
课堂讨论:
1).作简谐振动的物体在平衡位置所受合外力 一定为零吗?
2). 判断此小球是否作简谐振动。
1)物体受线性回复力(矩)作用
平衡位置
平衡位置不等于平衡状态,是指回复力为零的位置,物体在该位置所受的合外力不一定为零。
1、振幅 A
简谐振动物体离开平衡位置的最大位移(或角位移)的绝对值。
初始条件
4-2 描述简谐振动的物理量
A
A
频率 :单位时间内全振动的次数。
2、周期 、频率、角频率
对弹簧振子
角频率
固有周期、固有频率、固有角频率
周期T :物体完成一次全振动所需时间。
单摆
复摆
0 是t =0时刻的位相—初相位
3、相位和初相位
—相位,决定简谐振动物体的运动状态
4. 相位差
=( 2 t+ 2)-( 1 t+ 1)
对两同频率的谐振动 = 2- 1
初相差
同相和反相
t
x
o
A1
-A1
A2
- A2
x1
x2
T
同相
当 =2k ,k=0,±1,±2…,两振动步调相同,称同相
x2
T
x
o
A1
-A1
A2
- A2
x1
t
反相
当 =(2k+1) , k=0,±1,±2... 两振动步调相反,称反相
2 超前于 1 或 1滞后于 2
相位差反映了两个振动不同程度的参差错落
例1:一弹簧振子系统,弹簧的劲度系数为k=0.72N/m,物体的质量为m=20g。今将物体从平衡位置沿桌面向右拉长到0.04m处,由静止释放,求振动方程。
又因为x0为正,初速度v0=0,可得
因而简谐振动的方程为:
解:设 ,只要确定A、ω和 0即可。由题可知,k=0.72N/m,m=20g=0.02kg,x0=0.04m,v0=0,代入公式可得
R
M
m
k
O
X
x
旋转矢量法
A
A
X
X
O
j
M ( 0 )
A
j
初相
M ( t )
t
w
t
w
M ( t )
t
w
M ( t )
t
w
M ( t )
M ( t )
t
w
M ( t )
t
w
M (T )
T
w
周期 T
M ( t )
t
w
M ( t )
t
w
X
O
j
M ( 0 )
j
初相
M ( t )
t
w
A
循环往复
4-3 简谐振动的旋转矢量表示法
旋转
矢量 的
端点在
轴上的投
影点的运
动为简谐
运动.
x
0
t+ 0
O
p
t=0
M
说明:
旋转矢量法是研究简谐振动的一种直观方法;
不能把M的运动误认为简谐振动。
模 振幅A
作坐标轴ox ,自原点作一矢量
与x 轴的夹角 相位
角速度 角频率
初始与x 轴的夹角 初相
旋转矢量 简谐振动
(旋转矢量旋转一周所需的时间)
用旋转矢量图画简谐运动的 图
P点坐标、速度和加速度都作简谐振动
矢端M在x 轴投影的运动规律:
P点的坐标
即M点位矢在x 轴上的投影
速度
即M点速率在x 轴上的投影
加速度
即M点向心加速度在x 轴上的投影
0
t+ 0
O
p
t=0
M
用旋转矢量表示相位关系
同相
反相
谐振动的位移、速度、加速度之间的位相关系
t
o
T
a
v
x
T/4
T/4
由图可见:
x
t+
o
·
例. 已知简谐振动 , 当 时位
移为 且向 负向运动。
求(1)振动方 程。
(2) 且向 正向运动时的速度、加速
度及从这一位置回到平衡位置的最小时间。
解(1)
由旋转矢量 得
(2)先求 由旋转矢量法
(半个周期)
o
由旋转矢量法
(用解析法也可求出!)
例. 已知 x t 曲线,写出振动方程,
并求它们的位相差?
x
解:
或
或
位相差反映了两振动达到同一状态有时间差
讨论:
例 已知某简谐振动的 速度与时间的关系曲线如图所示,试求其振动方程。
解:方法1
设振动方程为
故振动方程为
方法2:
用旋转矢量法辅助求解。
v的旋转矢量与v轴夹角表示t 时刻相位
由图知
以弹簧振子为例
谐振动系统的能量=系统的动能Ek+系统的势能Ep
某一时刻,谐振子速度为v,位移为x
谐振动的动能和势能是时间的周期性函数
4-4 简谐振动的能量
动能
势能
情况同动能。
机械能
简谐振动系统机械能守恒
例七
该摆动系统的机械能守恒数学表达式
该摆的运动学微分方程及摆动周期
动能 刚体(直棒)转动动能
势能 系统的重力势能
以垂态直棒中心点 C 为重力零势点
令
机械能
机械能守恒,即 为恒量,
即
得 简谐角振动微分方程
该摆的振动周期
匀质细直悬棒
质量 m、长 L
在铅直面内摆动
摆幅很小
转动惯量
4-5 简谐振动的合成
某质点同时参与两个同频率且在同一条直线上的简谐运动
合振动
1、应用解析法
令
一、两个同方向同频率简谐运动的合成
2、应用旋转矢量法
x
y
合成振动
是简谐运动
3、讨论
合振幅最大
情况1
当 称为干涉相长
情况2
合振幅最小
当 称为干涉相消
情况3:一般情况
质点同时参与两个不同频率但在同一条直线上的简谐振动
合振动
假设
1
o
x
2
二、同方向不同频率的简谐振动的合成
合成振动表达式:
合振动是振幅按 |2A0cos2π(ν2-ν1)t/2| 缓慢变化的频率为(ν2+ν1)/2 的“准周期运动”
x
t
x2
t
x1
t
1 )单位时间内振动加强或减弱的次数叫拍频
2)合振动的“频率”为
其振幅变化的周期是由振幅绝对值变化来决定,即振动忽强忽弱。这种合振动忽强忽弱的现象称为拍。
拍现象的应用:
用标准音叉振动校准乐器
测定超声波
测定无线电频率
调制高频振荡的振幅和频率等
385 Hz
383 Hz
听到的音频
384 Hz
强度节拍性变化
2 Hz
四、两个相互垂直的同频率简谐振动的合成
某质点同时参与两个同频率的互相垂直方向的简谐运动
合振动的轨迹方程为
是个椭圆方程,具体形状由相位差决定。
讨论1
合振动的轨迹是一条通过原点的直线
讨论2
合振动的轨迹是一条通过原点的直线
讨论3
合振动的轨迹是椭圆方程,且顺时针旋转
讨论4
合振动的轨迹是椭圆方程,且逆时针旋转
讨论5
合振动的轨迹是的圆
讨论6
则为任一椭圆方程
综上所述:两个频率相同的互相垂直的简谐振动合成后,合振动在一直线上或者在椭圆上进行当两个分振动的振幅相等时,椭圆轨道就成为圆。
续上
或
为任意值时,合振动的轨迹一般为椭圆
五、两个垂直方向不同频率简谐运动的合成
合成运动不是周期性的运动。下面就两种情况讨论
视为同频率的合成:两个振动的相位差缓慢地变化,质点运动的轨道循环变化。
情况1:两个分振动的频率相差很小
合成运动的轨道是封闭曲线,运动也具有周期。这种运动轨迹的图形称为李萨如图形。
情况2:两个分振动的频率相差较大,有简单整数比关系
例如
由切点数之比
可测频率。
例4 有两个振动方向相同的简谐振动,其振动方程分别为 ,
1) 求它们的合振动方程;
问: 当 3为何值时, x1+x3的振动为最大值?当 3为何值时, x1+x3的振动为最小值?
解:1) 两个振动方向相同, 频率相同的简谐振动合成后还是简谐振动, 合振动方程为
2) 另有一同方向的简谐振动
所求的振动方程为
2)
当 时,相位相同。
当 时,相位相反。
根据已知条件,t=0时,合矢量应在第二象限,故
一、 阻尼振动
阻尼振动
能量随时间减小的振动称阻尼振动或减幅振动。
摩擦阻尼:
系统克服阻力作功使振幅受到摩擦力的作用,系统的动能转化为热能。
辐射阻尼:
振动以波的形式向外传波,使振动能量向周围辐射出去。
4-5 阻尼振动 受迫振动 共振
阻尼振动的振动方程(系统受到弱介质阻力而衰减)
振子动力学方程
振子受阻力
系统固有角频率
阻尼系数
弱介质阻力是指振子运动速度较低时,
介质对物体的阻力仅与速度的一次方成正比
—阻力系数
弱阻尼
弱阻尼
每一周期内损失的能量越小,振幅衰减越慢,周期越接近于谐振动。
阻尼振动的振幅按指数衰减
阻尼振动的准周期
临界阻尼
临界阻尼
系统不作往复运动,而是较快地回到平衡位置并停下来
过阻尼
过阻尼
系统不作往复运动,而是非常缓慢地回到平衡位置
二、 受迫振动
受迫振动 振动系统在周期性外力作用下的振动。
弱阻尼谐振子系统在策动力作用下的受迫振动的方程
令
周期性外力——策动力
稳定解
(1)频率: 等于策动力的频率
(2)振幅:
(3)初相:
特点:稳态时的受迫振动按简谐振动的规律变化
阻尼振动
简谐振动
三、共振
在一定条件下, 振幅出现极大值, 振动剧烈的现象。
1、位移共振
(1)共振频率 :
(2)共振振幅 :
2、速度共振
一定条件下, 速度振幅极大的现象。
速度共振时,速度与策动力同相,一周期内策动力总作正功,此时向系统输入的能量最大。
共振现象的危害
1940 年11月7日美国 Tocama 悬索桥因共振而坍塌
