1.4.1 用空间向量研究直线、平面的平行关系 同步练习-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(含答案)
文档属性
| 名称 | 1.4.1 用空间向量研究直线、平面的平行关系 同步练习-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 12:28:33 | ||
图片预览

文档简介
用空间向量研究直线、平面的平行关系
基础巩固
1.已知平面α的一个法向量是(2,3,-1),平面β的一个法向量是(4,λ,-2),若α∥β,则实数λ的值是( )
A.- B.6 C.-6 D.
2.设a=(3,-2,-1)是直线l的一个方向向量,n=(1,2,-1)是平面α的一个法向量,则( )
A.l⊥α B.l∥α
C.l∥α或l α D.l α或l⊥α
3.已知平面α内的两条直线的方向向量分别为a=(1,2,1),b=(-1,1,2),则平面α的一个法向量为( )
A.(-1,-2,5) B.(-1,1,-1)
C.(1,1,1) D.(1,-1,-1)
4.如图,在正方体ABCD-A1B1C1D1中,M,N分别为A1B,AC的中点,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.不能确定
5.(多选题)如图,在平行六面体ABCD-A1B1C1D1中,M,P,Q分别为AB,CD,BC的中点.下列结论正确的是( )
A.A1M∥D1P
B.A1M∥B1Q
C.A1M∥平面DCC1D1
D.A1M∥平面D1PQB1
6.已知直线l∥平面α,且直线l的一个方向向量为m=(2,-8,1),平面α的一个法向量为n=(1,y,2),则y= .
7.已知A(4,1,3),B(2,3,1),C(3,7,-5),点P(x,-1,3)在平面ABC内,则x= ,= (用向量表示).
8.已知点O(0,0,0),A(4,1,3),B(2,3,1),C(3,7,-5),以=(x,-1,3)为方向向量的直线与平面ABC平行,则x= .
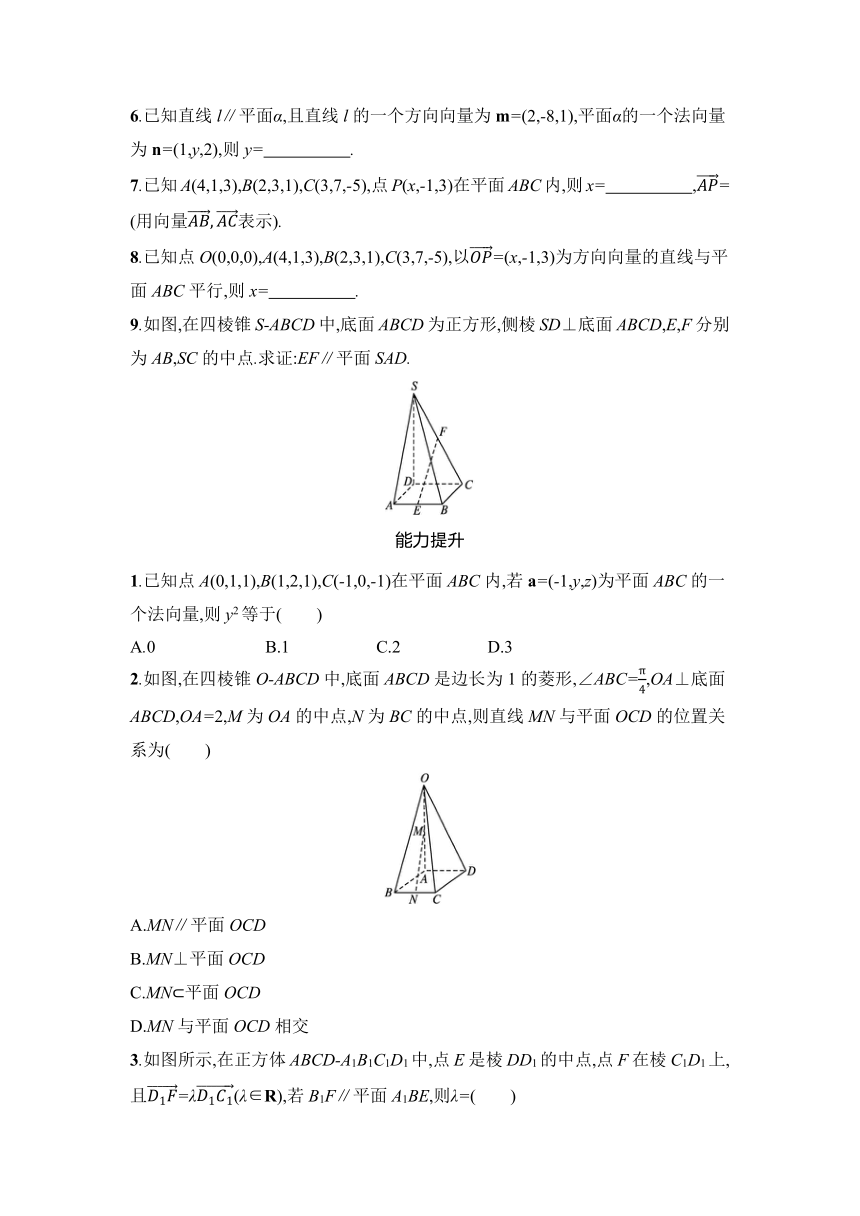
9.如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.求证:EF∥平面SAD.
能力提升
1.已知点A(0,1,1),B(1,2,1),C(-1,0,-1)在平面ABC内,若a=(-1,y,z)为平面ABC的一个法向量,则y2等于( )
A.0 B.1 C.2 D.3
2.如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点,则直线MN与平面OCD的位置关系为( )
A.MN∥平面OCD
B.MN⊥平面OCD
C.MN 平面OCD
D.MN与平面OCD相交
3.如图所示,在正方体ABCD-A1B1C1D1中,点E是棱DD1的中点,点F在棱C1D1上,且=λ(λ∈R),若B1F∥平面A1BE,则λ=( )
A. B. C. D.
4.若平面α的一个法向量为u1=(-3,y,2),平面β的一个法向量为u2=(6,-2,z),且α∥β,则y+z= .
5.如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,点M在EF上,且AM∥平面BDE,以C为原点,建立空间直角坐标系,则点M的坐标为 .
6.如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP=2,D为AP的中点,E,F,G分别为PC,PD,BC的中点,将△PCD沿CD折起,使得PD⊥平面ABCD.求证:AP∥平面EFG.
7.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=AD=1,问在棱PD上是否存在一点E,使CE∥平面PAB 若存在,求出点E的位置;若不存在,请说明理由.
参考答案
基础巩固
1. B
2. C
3. B
4.B
5.ACD
6.
7. 11 -4
8. -4
9.
证明:如图,以D为原点,DA,DC,DS所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.
设AB=a,SD=b,则E(a,,0),F(0,),
所以=(-a,0,).
由题意可知,CD⊥平面SAD,故=(0,a,0)为平面SAD的一个法向量.
因为=0,EF 平面SAD,
所以EF∥平面SAD.
能力提升
1. B
2. A
3. C
4.-3
5.
6.
证明:如图,以D为原点,DA,DC,DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
则P(0,0,2),G(1,2,0),E(0,1,1),F(0,0,1),A(2,0,0),所以=(-2,0,2),=(0,-1,0),=(1,1,-1).
设平面EFG的法向量为n=(x,y,z),
则
所以
令z=1,则x=1.
所以n=(1,0,1)为平面EFG的一个法向量.
因为n·=1×(-2)+0×0+1×2=0,AP 平面EFG,所以AP∥平面EFG.
7.
解:存在一点E,使CE∥平面PAB,此时E为PD的中点.理由如下:
如图,以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,则由题意可知,P(0,0,1),C(1,1,0),D(0,2,0),平面PAB的一个法向量为n=(0,1,0),所以=(-1,-1,1),=(0,2,-1).
设=λ(0≤λ≤1),则=(-1,2λ-1,1-λ).
若CE∥平面PAB,则·n=0,即2λ-1=0,所以λ=,此时E为PD的中点.
故在棱PD上存在一点E,使CE∥平面PAB,此时E为PD的中点.
基础巩固
1.已知平面α的一个法向量是(2,3,-1),平面β的一个法向量是(4,λ,-2),若α∥β,则实数λ的值是( )
A.- B.6 C.-6 D.
2.设a=(3,-2,-1)是直线l的一个方向向量,n=(1,2,-1)是平面α的一个法向量,则( )
A.l⊥α B.l∥α
C.l∥α或l α D.l α或l⊥α
3.已知平面α内的两条直线的方向向量分别为a=(1,2,1),b=(-1,1,2),则平面α的一个法向量为( )
A.(-1,-2,5) B.(-1,1,-1)
C.(1,1,1) D.(1,-1,-1)
4.如图,在正方体ABCD-A1B1C1D1中,M,N分别为A1B,AC的中点,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.不能确定
5.(多选题)如图,在平行六面体ABCD-A1B1C1D1中,M,P,Q分别为AB,CD,BC的中点.下列结论正确的是( )
A.A1M∥D1P
B.A1M∥B1Q
C.A1M∥平面DCC1D1
D.A1M∥平面D1PQB1
6.已知直线l∥平面α,且直线l的一个方向向量为m=(2,-8,1),平面α的一个法向量为n=(1,y,2),则y= .
7.已知A(4,1,3),B(2,3,1),C(3,7,-5),点P(x,-1,3)在平面ABC内,则x= ,= (用向量表示).
8.已知点O(0,0,0),A(4,1,3),B(2,3,1),C(3,7,-5),以=(x,-1,3)为方向向量的直线与平面ABC平行,则x= .
9.如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.求证:EF∥平面SAD.
能力提升
1.已知点A(0,1,1),B(1,2,1),C(-1,0,-1)在平面ABC内,若a=(-1,y,z)为平面ABC的一个法向量,则y2等于( )
A.0 B.1 C.2 D.3
2.如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点,则直线MN与平面OCD的位置关系为( )
A.MN∥平面OCD
B.MN⊥平面OCD
C.MN 平面OCD
D.MN与平面OCD相交
3.如图所示,在正方体ABCD-A1B1C1D1中,点E是棱DD1的中点,点F在棱C1D1上,且=λ(λ∈R),若B1F∥平面A1BE,则λ=( )
A. B. C. D.
4.若平面α的一个法向量为u1=(-3,y,2),平面β的一个法向量为u2=(6,-2,z),且α∥β,则y+z= .
5.如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,点M在EF上,且AM∥平面BDE,以C为原点,建立空间直角坐标系,则点M的坐标为 .
6.如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP=2,D为AP的中点,E,F,G分别为PC,PD,BC的中点,将△PCD沿CD折起,使得PD⊥平面ABCD.求证:AP∥平面EFG.
7.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=AD=1,问在棱PD上是否存在一点E,使CE∥平面PAB 若存在,求出点E的位置;若不存在,请说明理由.
参考答案
基础巩固
1. B
2. C
3. B
4.B
5.ACD
6.
7. 11 -4
8. -4
9.
证明:如图,以D为原点,DA,DC,DS所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.
设AB=a,SD=b,则E(a,,0),F(0,),
所以=(-a,0,).
由题意可知,CD⊥平面SAD,故=(0,a,0)为平面SAD的一个法向量.
因为=0,EF 平面SAD,
所以EF∥平面SAD.
能力提升
1. B
2. A
3. C
4.-3
5.
6.
证明:如图,以D为原点,DA,DC,DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
则P(0,0,2),G(1,2,0),E(0,1,1),F(0,0,1),A(2,0,0),所以=(-2,0,2),=(0,-1,0),=(1,1,-1).
设平面EFG的法向量为n=(x,y,z),
则
所以
令z=1,则x=1.
所以n=(1,0,1)为平面EFG的一个法向量.
因为n·=1×(-2)+0×0+1×2=0,AP 平面EFG,所以AP∥平面EFG.
7.
解:存在一点E,使CE∥平面PAB,此时E为PD的中点.理由如下:
如图,以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,则由题意可知,P(0,0,1),C(1,1,0),D(0,2,0),平面PAB的一个法向量为n=(0,1,0),所以=(-1,-1,1),=(0,2,-1).
设=λ(0≤λ≤1),则=(-1,2λ-1,1-λ).
若CE∥平面PAB,则·n=0,即2λ-1=0,所以λ=,此时E为PD的中点.
故在棱PD上存在一点E,使CE∥平面PAB,此时E为PD的中点.
