人教版2021-2022学年九年级数学下册27.1图形的相似 课后自主提升训练(word版、含解析)
文档属性
| 名称 | 人教版2021-2022学年九年级数学下册27.1图形的相似 课后自主提升训练(word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 289.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览



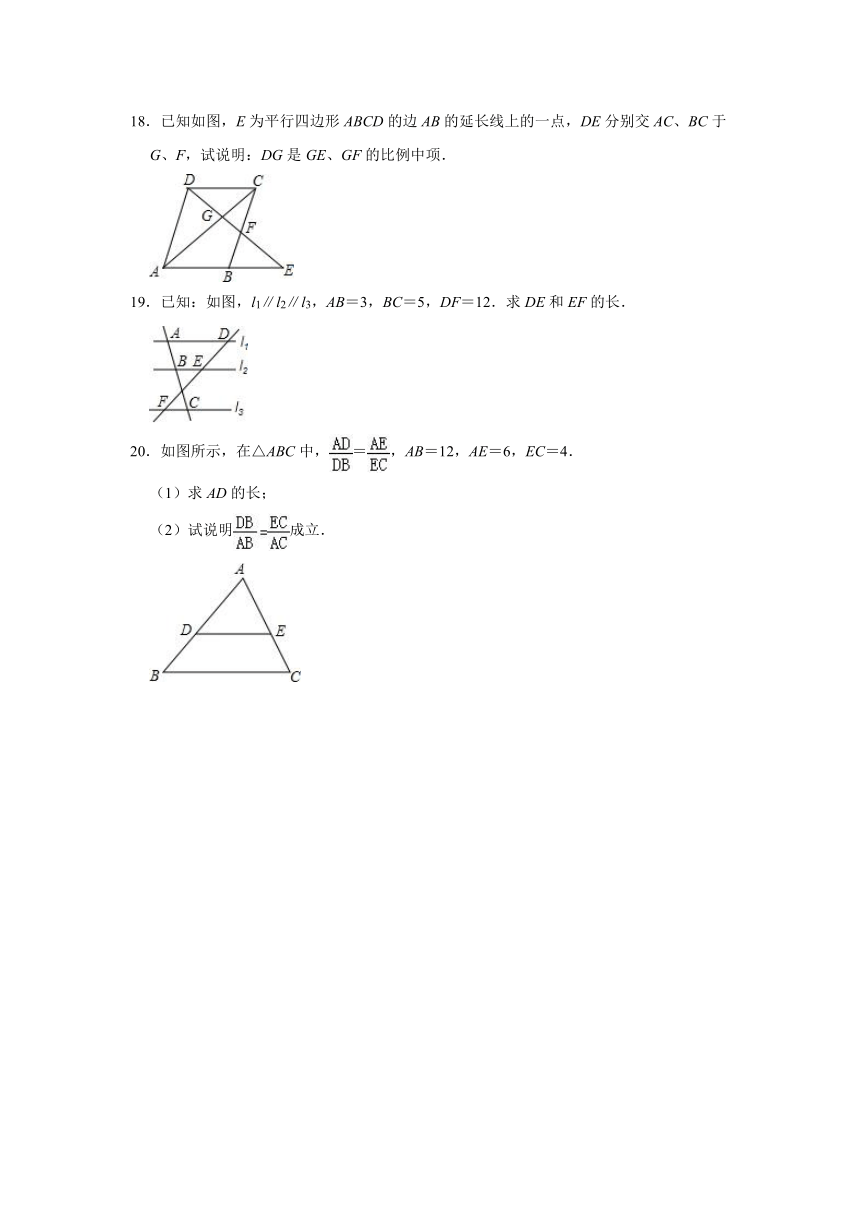
文档简介
2021-2022学年人教版九年级数学下册《27.1图形的相似》课后自主提升训练(附答案)
1.若3x﹣2y=0,则+1等于( )
A. B. C. D.﹣
2.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则=( )
A. B.2 C. D.
3.如图,已知DE∥BC,EF∥AB,现得到下列结论:
①;②;③;④.
其中正确比例式的个数有( )
A.4个 B.3个 C.2个 D.1个
4.如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,EF∥CD交AB于F,那么下列比例式中正确的是( )
A. B. C. D.
5.下列各组图形一定相似的是( )
A.两个矩形
B.两个等边三角形
C.各有一角是80°的两个等腰三角形
D.任意两个菱形
6.下列说法中正确的有( )
①位似图形都相似;
②两个等腰三角形一定相似;
③两个相似多边形的面积比为4:9,则周长的比为16:81;
④若一个三角形的三边分别比另一个三角形的三边长2cm,那么这两个三角形一定相似.
A.1个 B.2个 C.3个 D.4个
7.如果a=3,c=12,则a与c的比例中项是 .
8.如图,点D、E、F分别位于△ABC的三边上,满足DE∥BC,EF∥AB,如果AD:DB=3:2,那么BF:FC= .
9.(1)已知=,求的值.
(2)已知==,求的值.
10.如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)求证:BC2=AC CD;
(2)求∠ABD的度数.
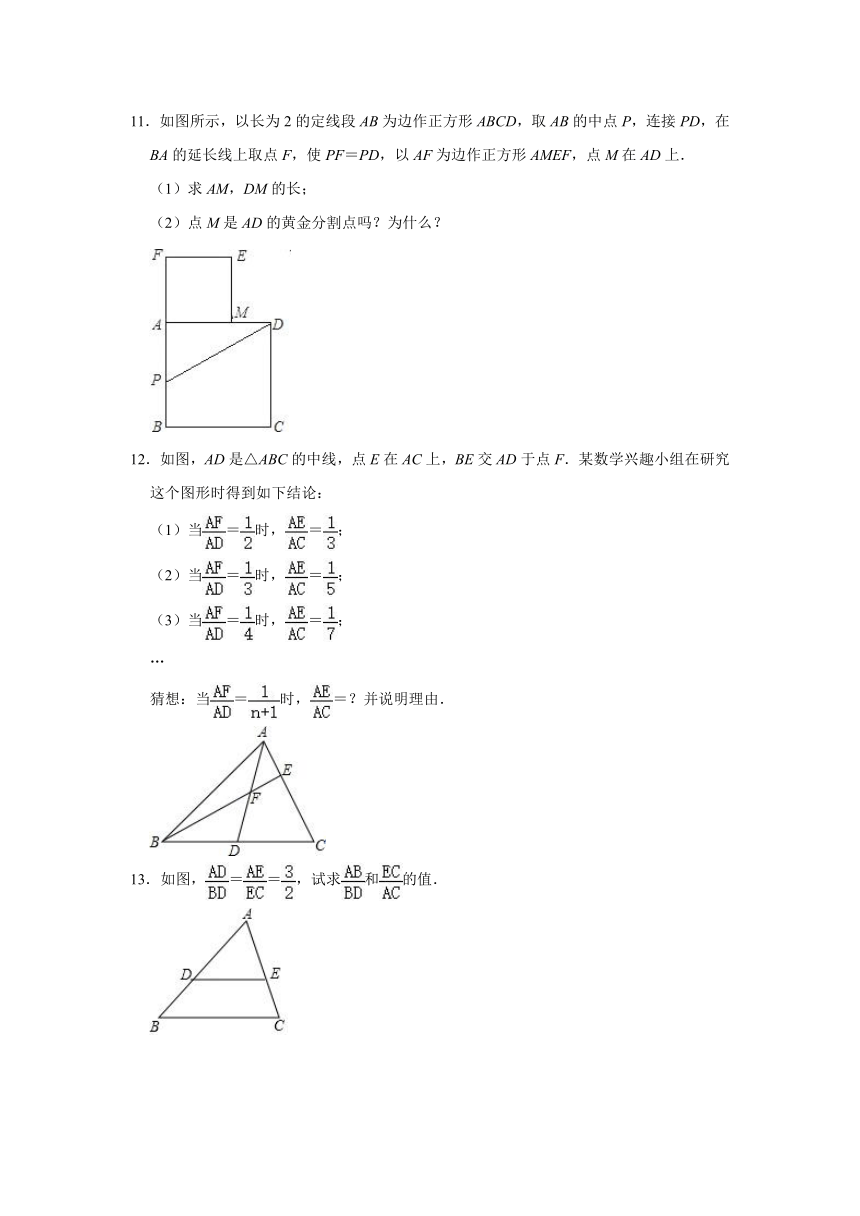
11.如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)点M是AD的黄金分割点吗?为什么?
12.如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:
(1)当=时,=;
(2)当=时,=;
(3)当=时,=;
…
猜想:当=时,=?并说明理由.
13.如图,==,试求和的值.
14.在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
(1)求的值;
(2)若BD=5,求CQ的长.
15.已知,如图,点A,B,C分别在△EFD的各边上,且AB∥DE,BC∥EF,CA∥FD,求证:A,B,C分别是△EFD各边的中点.
16.如图,BC∥ED,BD、CE相交于点A,且DE=4,BC=8.
(1)若AE=2,求AC的长;
(2)若BD=9,求AB的长.
17.如图,△ABC中,BD是角平分线,过D作DE∥AB交BC于点E,AB=5cm,BE=3cm,分别求出DE与EC的长.
18.已知如图,E为平行四边形ABCD的边AB的延长线上的一点,DE分别交AC、BC于G、F,试说明:DG是GE、GF的比例中项.
19.已知:如图,l1∥l2∥l3,AB=3,BC=5,DF=12.求DE和EF的长.
20.如图所示,在△ABC中,=,AB=12,AE=6,EC=4.
(1)求AD的长;
(2)试说明成立.
参考答案
1.解:由题意,得
3x=2y.
两边都除以3y,得
=.
+1=+1=,
故选:C.
2.解:∵AH=2,HB=1,
∴AB=AH+BH=3,
∵l1∥l2∥l3,
∴==.
故选:A.
3.解:∵EF∥AB,
∴=,=,
即=,
∵DE∥BC,
∴==,
即=,
=≠,
所以①②④正确,故题中正确的个数为3个.
故选:B.
4.解:A、∵EF∥CD,DE∥BC,
∴,,
∵CE≠AC,
∴.故本答案错误;
B、∵DE∥BC,EF∥CD,
∴,,
∴,
∵AD≠DF,
∴,故本答案错误;
C、∵EF∥CD,DE∥BC,
∴,,
∴.
∵AD≠DF,
∴,故本答案错误;
D、∵DE∥BC,EF∥CD,
∴,,
∴,故本答案正确.
故选:D.
5.解:两个矩形对应边的比不一定相等,故不一定相似;
两个等边三角形相似对应边的比相等,对应角相等,一定相似;
各有一角是80°的两个等腰三角形对应角不一定相等,故不一定相似;
任意两个菱形对应角不一定相等,故不一定相似;
故选:B.
6.解:①正确.
②两个等腰三角形一定相似,错误不一定相似.
③两个相似多边形的面积比为4:9,则周长的比为16:81,错误周长比应该是2:3,
④不相似,三边不一定成比例.
故选:A.
7.解:∵b是a、c的比例中项,
∴b2=ac,
即b2=3×12=36,
∴b=±6,
故答案为±6
8.解:∵DE∥BC,
∴=,
∵AD:DB=3:2,AB=AD+DB,
∴=,
∴=,
∵DE∥BC,EF∥AB,
∴四边形DEBF是平行四边形,
∴DE=BF,
∵BC=BF+CF,=,
∴=,
∴BF:CF=3:2,
故答案为3:2;
9.解:(1)∵=,
∴2b=1.5a,
∴==﹣;
(2)设===k(k≠0),则x=2k,y=3k,z=4k,
∴==.
10.解:(1)∵AD=BC,BC=,
∴AD=,
∵AB=AC=1,
∴CD==.
∴BC2=()2==,AC CD==.
∴BC2=AC CD.
(2)∵BC2=AC CD,
∴=.
又∵∠C=∠C,
∴△BCD∽△ACB.
∴==1,∠DBC=∠A.
∴BD=BC=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x°,则∠ABD=∠DBC=x°,∠C=∠BDC=2x°.
∵∠DBC+∠BDC+∠C=180°,
∴x+2x+2x=180,
解得x=36.
∴∠ABD=36°.
11.解:(1)在Rt△APD中,AP=1,AD=2,由勾股定理知PD===,
∴AM=AF=PF﹣AP=PD﹣AP=﹣1,
DM=AD﹣AM=3﹣.
故AM的长为﹣1,DM的长为3﹣;
(2)点M是AD的黄金分割点.
由于=,
∴点M是AD的黄金分割点.
12.解:猜想:当=时,=;理由如下:
如图,过点D作DG∥BE,交AC与点G;
则,
∴,EG=nAE;
∵AD是△ABC的中线,
∴EG=CG,AC=(2n+1)AE,
∴.
13.解:∵==,
∴=,
∴=,
∴=.
14.解:(1)设BD=x,则CD=2x,AD=3x,BC=BD+CD=3x,
∵AQ∥BC,
∴==1,
∴AQ=CD=2x,
∴==;
(2)∵BD=5,BD:CD:AD=1:2:3,
∴CD=10,AD=15,
∵E是AD的中点,
∴DE=AD=7.5,
由勾股定理得,CE==,
∴CQ=25.
15.证明:如图,∵AB∥DE,BC∥EF,CA∥FD,
∴四边形AFBC,四边形ABDC,四边形ABCE为平行四边形,
∴BF=CA,BD=AC,
∴BF=BD;同理可证:AF=AE,CD=CE,
∴A,B,C分别是△EFD各边的中点.
16.解:(1)∵BC∥ED,
∴,即,
解得:AC=4;
(2)∵BC∥ED,
∴==2,
∴AB=2AD,
∵BD=9,
∴AD=3,AB=6.
17.解:∵BD是角平分线,
∴∠ABD=∠CBD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠BDE=∠EBD,
∴DE=BE=3cm,
∵DE∥AB,
∴=,即=,解得CE=(cm).
答:DE与EC的长分别为3cm、cm.
18.解:∵四边形ABCD是平行四边形,
∴DC∥AE,
∴=,
∵AD∥BC,
∴=,
∴=,
∴DG2=GE GF,
∴DG是GE、GF的比例中项.
19.解:∵l1∥l2∥l3,
∴AB:BC=DE:EF,
∵AB=3,BC=5,DF=12,
∴3:5=DE:(12﹣DE),
∴DE=4.5,
∴EF=12﹣4.5=7.5.
20.解:(1)∵=,
∴=,
∴AD=;
(2)∵=,
∴=,即=,
∴.
1.若3x﹣2y=0,则+1等于( )
A. B. C. D.﹣
2.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则=( )
A. B.2 C. D.
3.如图,已知DE∥BC,EF∥AB,现得到下列结论:
①;②;③;④.
其中正确比例式的个数有( )
A.4个 B.3个 C.2个 D.1个
4.如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,EF∥CD交AB于F,那么下列比例式中正确的是( )
A. B. C. D.
5.下列各组图形一定相似的是( )
A.两个矩形
B.两个等边三角形
C.各有一角是80°的两个等腰三角形
D.任意两个菱形
6.下列说法中正确的有( )
①位似图形都相似;
②两个等腰三角形一定相似;
③两个相似多边形的面积比为4:9,则周长的比为16:81;
④若一个三角形的三边分别比另一个三角形的三边长2cm,那么这两个三角形一定相似.
A.1个 B.2个 C.3个 D.4个
7.如果a=3,c=12,则a与c的比例中项是 .
8.如图,点D、E、F分别位于△ABC的三边上,满足DE∥BC,EF∥AB,如果AD:DB=3:2,那么BF:FC= .
9.(1)已知=,求的值.
(2)已知==,求的值.
10.如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)求证:BC2=AC CD;
(2)求∠ABD的度数.
11.如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)点M是AD的黄金分割点吗?为什么?
12.如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:
(1)当=时,=;
(2)当=时,=;
(3)当=时,=;
…
猜想:当=时,=?并说明理由.
13.如图,==,试求和的值.
14.在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
(1)求的值;
(2)若BD=5,求CQ的长.
15.已知,如图,点A,B,C分别在△EFD的各边上,且AB∥DE,BC∥EF,CA∥FD,求证:A,B,C分别是△EFD各边的中点.
16.如图,BC∥ED,BD、CE相交于点A,且DE=4,BC=8.
(1)若AE=2,求AC的长;
(2)若BD=9,求AB的长.
17.如图,△ABC中,BD是角平分线,过D作DE∥AB交BC于点E,AB=5cm,BE=3cm,分别求出DE与EC的长.
18.已知如图,E为平行四边形ABCD的边AB的延长线上的一点,DE分别交AC、BC于G、F,试说明:DG是GE、GF的比例中项.
19.已知:如图,l1∥l2∥l3,AB=3,BC=5,DF=12.求DE和EF的长.
20.如图所示,在△ABC中,=,AB=12,AE=6,EC=4.
(1)求AD的长;
(2)试说明成立.
参考答案
1.解:由题意,得
3x=2y.
两边都除以3y,得
=.
+1=+1=,
故选:C.
2.解:∵AH=2,HB=1,
∴AB=AH+BH=3,
∵l1∥l2∥l3,
∴==.
故选:A.
3.解:∵EF∥AB,
∴=,=,
即=,
∵DE∥BC,
∴==,
即=,
=≠,
所以①②④正确,故题中正确的个数为3个.
故选:B.
4.解:A、∵EF∥CD,DE∥BC,
∴,,
∵CE≠AC,
∴.故本答案错误;
B、∵DE∥BC,EF∥CD,
∴,,
∴,
∵AD≠DF,
∴,故本答案错误;
C、∵EF∥CD,DE∥BC,
∴,,
∴.
∵AD≠DF,
∴,故本答案错误;
D、∵DE∥BC,EF∥CD,
∴,,
∴,故本答案正确.
故选:D.
5.解:两个矩形对应边的比不一定相等,故不一定相似;
两个等边三角形相似对应边的比相等,对应角相等,一定相似;
各有一角是80°的两个等腰三角形对应角不一定相等,故不一定相似;
任意两个菱形对应角不一定相等,故不一定相似;
故选:B.
6.解:①正确.
②两个等腰三角形一定相似,错误不一定相似.
③两个相似多边形的面积比为4:9,则周长的比为16:81,错误周长比应该是2:3,
④不相似,三边不一定成比例.
故选:A.
7.解:∵b是a、c的比例中项,
∴b2=ac,
即b2=3×12=36,
∴b=±6,
故答案为±6
8.解:∵DE∥BC,
∴=,
∵AD:DB=3:2,AB=AD+DB,
∴=,
∴=,
∵DE∥BC,EF∥AB,
∴四边形DEBF是平行四边形,
∴DE=BF,
∵BC=BF+CF,=,
∴=,
∴BF:CF=3:2,
故答案为3:2;
9.解:(1)∵=,
∴2b=1.5a,
∴==﹣;
(2)设===k(k≠0),则x=2k,y=3k,z=4k,
∴==.
10.解:(1)∵AD=BC,BC=,
∴AD=,
∵AB=AC=1,
∴CD==.
∴BC2=()2==,AC CD==.
∴BC2=AC CD.
(2)∵BC2=AC CD,
∴=.
又∵∠C=∠C,
∴△BCD∽△ACB.
∴==1,∠DBC=∠A.
∴BD=BC=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x°,则∠ABD=∠DBC=x°,∠C=∠BDC=2x°.
∵∠DBC+∠BDC+∠C=180°,
∴x+2x+2x=180,
解得x=36.
∴∠ABD=36°.
11.解:(1)在Rt△APD中,AP=1,AD=2,由勾股定理知PD===,
∴AM=AF=PF﹣AP=PD﹣AP=﹣1,
DM=AD﹣AM=3﹣.
故AM的长为﹣1,DM的长为3﹣;
(2)点M是AD的黄金分割点.
由于=,
∴点M是AD的黄金分割点.
12.解:猜想:当=时,=;理由如下:
如图,过点D作DG∥BE,交AC与点G;
则,
∴,EG=nAE;
∵AD是△ABC的中线,
∴EG=CG,AC=(2n+1)AE,
∴.
13.解:∵==,
∴=,
∴=,
∴=.
14.解:(1)设BD=x,则CD=2x,AD=3x,BC=BD+CD=3x,
∵AQ∥BC,
∴==1,
∴AQ=CD=2x,
∴==;
(2)∵BD=5,BD:CD:AD=1:2:3,
∴CD=10,AD=15,
∵E是AD的中点,
∴DE=AD=7.5,
由勾股定理得,CE==,
∴CQ=25.
15.证明:如图,∵AB∥DE,BC∥EF,CA∥FD,
∴四边形AFBC,四边形ABDC,四边形ABCE为平行四边形,
∴BF=CA,BD=AC,
∴BF=BD;同理可证:AF=AE,CD=CE,
∴A,B,C分别是△EFD各边的中点.
16.解:(1)∵BC∥ED,
∴,即,
解得:AC=4;
(2)∵BC∥ED,
∴==2,
∴AB=2AD,
∵BD=9,
∴AD=3,AB=6.
17.解:∵BD是角平分线,
∴∠ABD=∠CBD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠BDE=∠EBD,
∴DE=BE=3cm,
∵DE∥AB,
∴=,即=,解得CE=(cm).
答:DE与EC的长分别为3cm、cm.
18.解:∵四边形ABCD是平行四边形,
∴DC∥AE,
∴=,
∵AD∥BC,
∴=,
∴=,
∴DG2=GE GF,
∴DG是GE、GF的比例中项.
19.解:∵l1∥l2∥l3,
∴AB:BC=DE:EF,
∵AB=3,BC=5,DF=12,
∴3:5=DE:(12﹣DE),
∴DE=4.5,
∴EF=12﹣4.5=7.5.
20.解:(1)∵=,
∴=,
∴AD=;
(2)∵=,
∴=,即=,
∴.
