2021-2022学年苏科版九年级数学下册第5章二次函数5.1--5.2小节提优练习(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册第5章二次函数5.1--5.2小节提优练习(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 600.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 23:05:50 | ||
图片预览


文档简介
二次函数--5.1--5.2小节提优练习
一、选择题
将 的图象向右平移 个单位,再向下平移 个单位,所得函数的对称轴和最小值分别为
A. , B. , C. , D. ,
如图,, 分别为 图象上的两点,且直线 垂直于 轴.若 ,则直线 的解析式为
A. B. C. D.
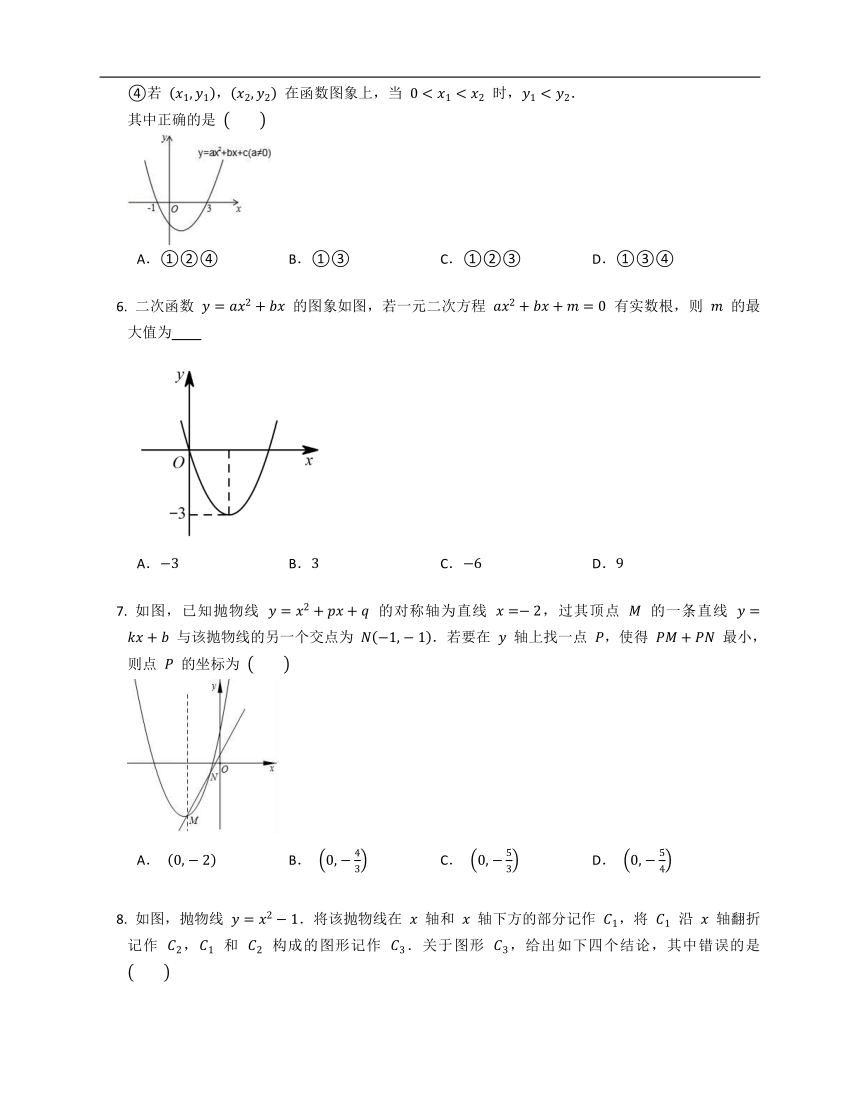
如图为二次函数 的图象,则下列说法:① ;② ;③ ;④ 当 时,.其中正确的个数为
A. B. C. D.
已知二次函数 ( 为常数),在自变量 的值满足 的情况下,与其对应的函数值 的最小值为 ,则 的值为
A. 或 B. 或 C. 或 D. 或
二次函数 的图象如图所示,下列说法:
① ;
②当 时,;
③ ;
④若 , 在函数图象上,当 时,.
其中正确的是
A.①②④ B.①③ C.①②③ D.①③④
二次函数 的图象如图,若一元二次方程 有实数根,则 的最大值为
A. B. C. D.
如图,已知抛物线 的对称轴为直线 ,过其顶点 的一条直线 与该抛物线的另一个交点为 .若要在 轴上找一点 ,使得 最小,则点 的坐标为
A. B. C. D.
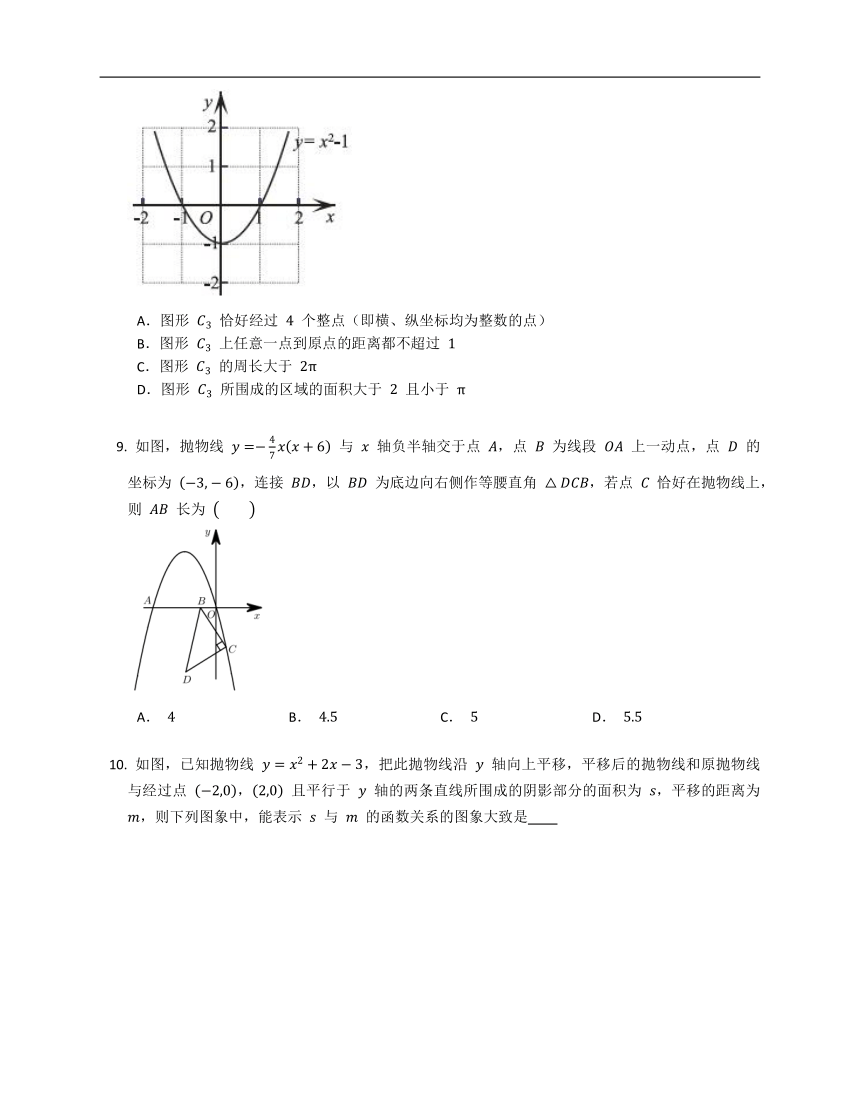
如图,抛物线 .将该抛物线在 轴和 轴下方的部分记作 ,将 沿 轴翻折记作 , 和 构成的图形记作 .关于图形 ,给出如下四个结论,其中错误的是
A.图形 恰好经过 个整点(即横、纵坐标均为整数的点)
B.图形 上任意一点到原点的距离都不超过
C.图形 的周长大于
D.图形 所围成的区域的面积大于 且小于
如图,抛物线 与 轴负半轴交于点 ,点 为线段 上一动点,点 的坐标为 ,连接 ,以 为底边向右侧作等腰直角 ,若点 恰好在抛物线上,则 长为
A. B. C. D.
如图,已知抛物线 ,把此抛物线沿 轴向上平移,平移后的抛物线和原抛物线与经过点 , 且平行于 轴的两条直线所围成的阴影部分的面积为 ,平移的距离为 ,则下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
二、填空题
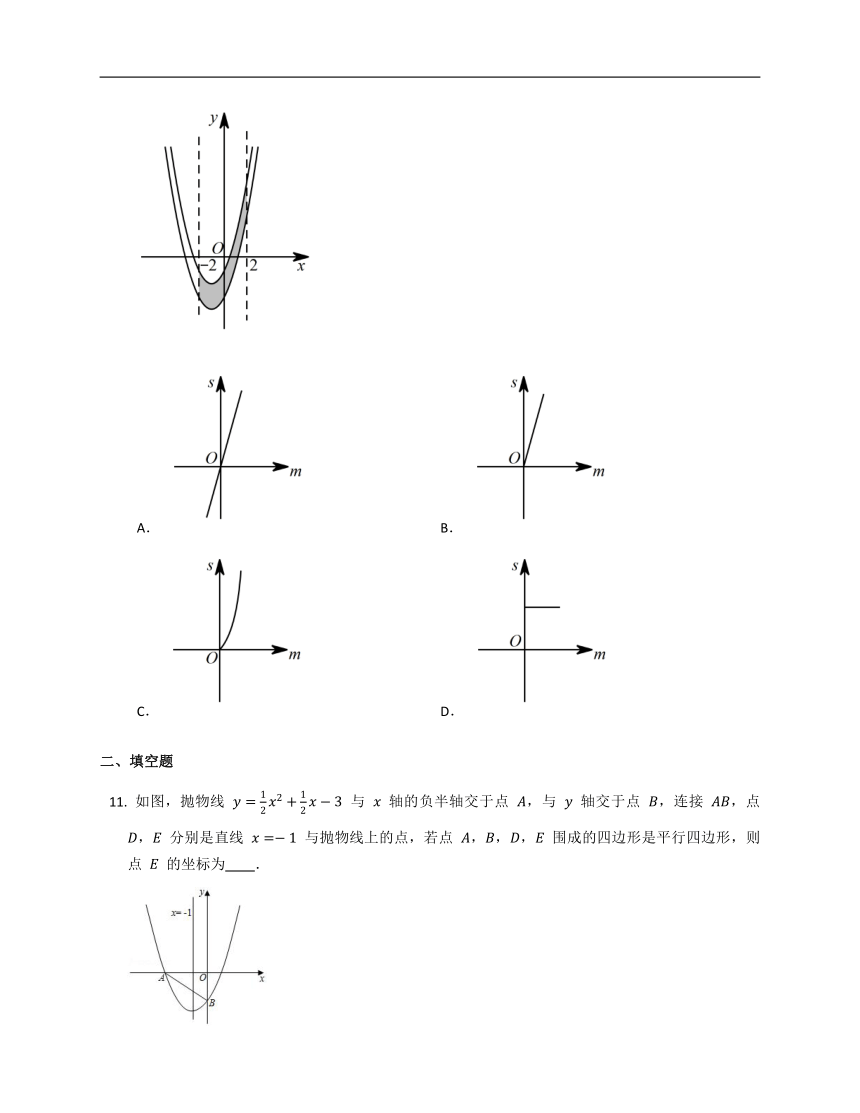
如图,抛物线 与 轴的负半轴交于点 ,与 轴交于点 ,连接 ,点 , 分别是直线 与抛物线上的点,若点 ,,, 围成的四边形是平行四边形,则点 的坐标为 .
如图,在平面直角坐标系中,二次函数 的图象过正方形 的三个顶点 ,,,则 的值是 .
已知二次函数 的图象与 轴交于 和 ,其中 ,与 轴交于正半轴上一点.下列结论:① ;② ;③ ;④ .其中正确结论的序号是 .
设抛物线 ,其中 为实数.
()若抛物线经过点 ,则 ;
()将抛物线 向上平移 个单位,所得抛物线顶点的纵坐标的最大值是 .
将抛物线 向上平移 个单位长度后,经过点 ,则 的值是 .
已知抛物线 过点 ,且抛物线上任意不同两点 , 都满足:当 时,;当 时,.以原点 为圆心, 为半径的圆与抛物线的另两个交点为 ,,且 在 的左侧, 有一个内角为 ,则抛物线的解析式为 .
已知当 和 时,多项式 的值相等,且 ,则当 时,多项式 的值等于 .
如图,一段抛物线:,记为 ,它与 轴交于点 ,;将 绕点 旋转 得 ,交 轴于点 ;将 绕点 旋转 得 ,交 轴于点 ; 如此进行下去,直至得 ,若 在第 段抛物线 上,则 的值为 .
三、解答题
已知函数 与 .
(1) 完成下表:
X -3 -2 -1 0 1 2 3
Y=-(x+1)2
Y=-(x-1)2
(2) 建立平面直角坐标系,并在坐标系中作出二次函数 与 的图象;
(3) 抛物线 与 之间有什么关系?它们是轴对称图形吗?它们的对称轴和顶点坐标分别是什么?
(4) 随 的增大, 分别是如何变化的?
已知在平面直角坐标系 中,二次函数 的图象经过点 和点 .
(1) 求这个二次函数的解析式;
(2) 将这个二次函数的图象向上平移,交 轴于点 ,其纵坐标为 ,请用 的代数式表示平移后函数图象顶点 的坐标;
(3) 在第()小题的条件下,如果点 的坐标为 , 平分 ,求 的值.
有一个二次函数满足以下条件:
①函数图象与 轴的交点坐标分别为 ,(点 在点 的右侧);
②对称轴是 ;
③该函数有最小值是 .
(1) 请根据以上信息求出二次函数表达式;
(2) 将该函数图象中 部分的图象向下翻折与原图象未翻折的部分组成图象“”,试结合图象分析:平行于 轴的直线 与图象“”的交点的个数情况.
如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点,与 轴交于点 .
(1) 若点 为直线 上方抛物线上的动点,当 的面积最大时,求此时 点的坐标;
(2) 若点 是抛物线对称轴上的动点,点 是抛物线上的动点,当以点 ,,, 为顶点的四边形是平行四边形时,直接写出此时 点的坐标.
有这样一个问题:探究函数 的图象与性质.
小东根据学习函数的经验,对函数 的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1) 函数 的自变量 的取值范围是 ;
(2) 下表是 与 的几组对应值.
X ··· -3 -2 -1 - - 1 2 3 ···
Y ··· - - - m ···
求 的值;
(3) 如下图,在平面直角坐标系 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4) 进一步探究发现,该函数图象在第一象限内的最低点的坐标是 ,结合函数的图象,写出该函数的其他性质(一条即可): .
如图,在平面直角坐标系 中,已知抛物线 经过点 ,对称轴是直线 ,顶点为点 ,抛物线与 轴交于点 .
(1) 求抛物线的表达式和点 的坐标;
(2) 将上述抛物线向下平移 个单位,平移后的抛物线与 轴正半轴交于点 ,求 的面积;
(3) 如果点 在原抛物线上,且在对称轴的右侧,连接 交线段 于点 ,,求点 的坐标.
将抛物线 向下平移 个单位长度得到抛物线 ,再将抛物线 向左平移 个单位长度得到抛物线 .
(1) 直接写出抛物线 , 的解析式;
(2) 如图(),点 在抛物线 对称轴 右侧上,点 在对称轴 上, 是以 为斜边的等腰直角三角形,求点 的坐标;
(3) 如图(),直线 (, 为常数)与抛物线 交于 , 两点, 为线段 的中点;直线 与抛物线 交于 , 两点, 为线段 的中点.求证:直线 经过一个定点.
对某一个函数给出如下定义:若存在实数 ,对于任意的函数值 ,都满足 ,则称这个函数是有界函数,在所有满足条件的 中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是 .
(1) 分别判断函数 和 是不是有界函数.若是有界函数,求其边界值.
(2) 若函数 (,)的边界值是 ,且这个函数的最大值也是 ,求 的取值范围.
(3) 将函数 (,)的图象向下平移 个单位,得到的函数的边界值是 ,当 在什么范围时,满足 .
如图 ,抛物线 与 轴交于 ,( 在 的左侧)两点,与 轴交于点 ,将直线 沿 轴正方向平移 个单位得到直线 ,将抛物线的对称轴沿 轴正方向平移 个单位得到直线 .
(1) 求直线 的解析式;
(2) 如图 ,点 为直线 上方抛物线上一动点,连接 , 与直线 分别交于点 ,,过点 作 于点 , 是线段 上一动点,过 作 于点 ,连接 ,当 的面积最大时,求 的最小值;
(3) 如图 ,连接 ,将 绕点 顺时针旋转 后得到 ,点 是直线 上一点,在直角坐标平面内是否存在一点 ,使得以点 ,,, 为顶点的四边形是矩形?若存在,求出点 的坐标;若不存在,请说明理由.
已知关于 的二次函数 在 和 时函数值相等.
(1) 求 的值.
(2) 若该二次函数的图象与直线 的一个交点为 ,求它的解析式.
(3) 在()的条件下,直线 与 轴, 轴分别交于点 ,,将线段 向右平移 个单位,同时将该二次函数在 的部分向左平移 个单位后得到的图象记为 ,请结合图象回答,当图象 与平移后的线段有公共点时, 的取值范围.
答案
一、选择题
1. 【答案】A
【解析】将 的图象向右平移 个单位,再向下平移 个单位,
所得图象的函数表达式是 即 ,
所以对称轴为 ,最小值为 .
【知识点】二次函数的图象变换、二次函数的图象与性质
2. 【答案】C
【知识点】二次函数的图象与性质、一次函数的解析式
3. 【答案】C
【解析】①开口向下,故 ,①错误;
②对称轴为直线 ,故 ,,,②正确;
③当 时,,③正确
④由图得,当 时,,④正确.
【知识点】二次函数的图象与性质
4. 【答案】B
【解析】二次函数的对称轴为直线 ,以下分情况讨论.
当 时,当 时, 取得最小值,即 ,解得 ,(舍去);
当 时,当 时, 取得最小值 ,不符合题意;
当 时,当 时, 取得最小值,即 ,解得 ,(舍去).
综上所述,.
【知识点】二次函数的最值
5. 【答案】B
【解析】 函数图象的对称轴为:,
,即 ,①正确;
由图象可知,当 时,,②错误;
由图象可知,当 时,,
,
,
,③正确;
抛物线的对称轴为 ,开口方向向上,
若 , 在函数图象上,
当 时,;当 时,,
故④错误.
【知识点】二次函数的图象与性质
6. 【答案】B
【解析】提示:令 ,则 是由二次函数 向上平移 个单位得到的函数,由图象可知二次函数 向上平移三个单位后与 轴只有一个交点,再向上平移没有交点,所以 的最大值为 .
【知识点】二次函数的图象与性质
7. 【答案】B
【解析】如图,作 点关于 轴的对称点 ,连接 交 轴于 点.
将 点坐标代入抛物线,并联立对称轴,
得 解得
,
, 点关于 轴的对称点 ,
设 的解析式为 ,
将 , 代入函数解析式,
得 解得
的解析式为 ,
当 时,,即 .
【知识点】轴对称之最短路径、二次函数的图象与性质、一次函数的解析式
8. 【答案】C
【知识点】二次函数的图象变换
9. 【答案】C
【解析】由题意,作 轴,,垂足分别为 ,.
设 点坐标为 ,
则 ,,
为等腰直角三角形,
,,
,
,
,
在 与 中,
,
,
,
,,(舍去),
,,
,
,
,
,
,
.
【知识点】二次函数的图象与性质、角角边
10. 【答案】B
【解析】如图,作出抛物线的对称轴 .
因为抛物线是上下平移,所以两个抛物线是同一条对称轴.
设对称轴与两抛物线分别交于 、 两点,直线 与抛物线交于 、 ,直线 与抛物线交于 、 ,则 ,
所以阴影部分的面积等于两个平行四边形的面积之和,即 .
【知识点】平行四边形、函数关系的表示、二次函数的图象变换
二、填空题
11. 【答案】 或 或
【解析】 抛物线 与 轴的负半轴交于点 ,与 轴交于点 ,
,.
当 为平行四边形的边时,,且 ,
线段 可由线段 平移得到.
点 在直线 上,
①当点 的对应点为 时,如图,
需先将 向左平移 个单位长度,此时点 的对应点 的横坐标为 ,
将 代入 ,得 ,
.
②当点 的对应点为 时,
同理,先将 向右平移 个单位长度,可得点 的对应点 的横坐标为 ,
将 代入 ,得 ,
;
当 为平行四边形的对角线时,可知 的中点坐标为 ,
在直线 上,
根据对称性可知 的横坐标为 ,
将 代入 ,得 ,
.
综上所述,点 的坐标为 或 或 .
【知识点】平行四边形的判定、二次函数的图象与性质、二次函数与方程
12. 【答案】
【知识点】二次函数的图象与性质、勾股定理、正方形的性质
13. 【答案】②④
【解析】 抛物线与x轴的交点为 和 ,,与 轴交于正半轴,
.
,
.
,,故①错误,③错误;
抛物线与 轴有两个交点,
.
,故②正确;
抛物线与 轴的交点有一个为 ,
.
.
,(已证),
,.
,,
,故④正确.
【知识点】二次函数的图象与性质
14. 【答案】 ;
【解析】()点 代入抛物线解析式 ,
得 ,解得 .
() 向上平移 个单位可得,,
所以 ,
所以抛物线顶点的纵坐标 ,
因为 ,
所以 的最大值为 .
【知识点】二次函数图像上点的坐标特征、二次函数的图象变换、二次函数的顶点
15. 【答案】
【解析】将抛物线 向上平移 个单位长度后,
表达式为:,
经过点 ,代入得:,
则 .
【知识点】二次函数的图象变换
16. 【答案】
【解析】 抛物线过点 ,
,
当 时,,由 ,得到 ,
当 时, 随 的增大而增大,
同理当 时, 随 的增大而减小,
抛物线的对称轴为 轴,且开口向下,即 ,
以 为圆心, 为半径的圆与抛物线交于另两点 ,,如图所示,
为等腰三角形,
中有一个角为 ,
为等边三角形,且 ,
设线段 与 轴的交点为点 ,则有 ,且 ,
,,
在 的左侧,
的坐标为 ,
点在抛物线上,且 ,,
,
解得:,
则抛物线解析式为 .
【知识点】解直角三角形、二次函数的图象与性质、圆的对称性
17. 【答案】
【解析】 和 时,多项式 的值相等,
二次函数 的对称轴为直线 ,
二次函数 的对称轴为直线 ,
,
,,
当 时,.
【知识点】二次函数的图象与性质
18. 【答案】
【解析】令 ,则 ,解得 ,,
,
由图可知,抛物线 在 轴下方,
相当于抛物线 向右平移 个单位得到 ,
再将 绕点 旋转 得 ,
抛物线 解析式为 ,
在第 段抛物线 上,
.
【知识点】二次函数的图象变换
三、解答题
19. 【答案】
(1) 略
(2) 略
(3) 抛物线 和 都可以看作是由 平移得到的,即它们的开口方向相同、开口大小相同,形状相同.它们是轴对称图形,它们的对称轴分别是直线 ,,顶点坐标分别是 ,.
(4) 二次函数 : 时, 随 增大而减小, 时, 随 增大而增大;二次函数 : 时, 随 增大而减小, 时, 随 增大而增大.
【知识点】描点法画二次函数图像、y=a(x-h)^2的图象、二次函数的增减性、二次函数的图象变换
20. 【答案】
(1) .
(2) .
(3) .
【知识点】二次函数的解析式、角平分线的性质、二次函数的顶点、二次函数的图象变换、二次函数与方程、坐标平面内图形轴对称变换
21. 【答案】
(1) 由上述信息可知该函数图象的顶点坐标为 ,
设二次函数的表达式为 .
该函数图象经过点 ,
,解得 .
二次函数解析式为 .
(2) 如图所示.
当 时,直线 与 有一个交点;
当 时,直线 与 有两个交点;
当 时,直线 与 有三个交点;
当 时,直线 与 有两个交点;
当 时,直线 与 有一个交点.
【知识点】二次函数的图象变换、二次函数的解析式
22. 【答案】
(1) 抛物线 与 轴交于 , 两点,
,
,,
点 的坐标为 ,点 的坐标为 ,
抛物线 与 轴交于点 ,
点 的坐标为 ,
点 的坐标为 ,点 的坐标为 ,
直线 解析式为:.
如图,过点 作 ,交 于点 ,
设点 ,则点 ,
,
的面积 ,
当 时, 的面积有最大值,
点 .
(2) 点 的坐标为 或 或 .
【解析】
(2) 设点 坐标为 ,
点 的坐标为 ,点 的坐标为 ,
抛物线的对称轴为直线 ,
点 是抛物线对称轴上的动点,
设点 坐标为 ,
当 为边时,则四边形 是平行四边形或四边形 是平行四边形,
若四边形 是平行四边形,
与 互相平分,
,,
,,
,
,
点 坐标为 ;
若四边形 是平行四边形,
与 互相平分,
,,
,,
,
,
点 坐标为 ;
当 为对角线时,
以点 ,,, 为顶点的四边形是平行四边形,
与 是互相平分,
,,
,,
,
,
点 坐标为 .
综上所述:点 的坐标为 或 或 .
【知识点】二次函数的图象与性质、平行四边形的判定、二次函数与方程
23. 【答案】
(1)
(2) 令 ,
,
.
(3) 如图,
(4) 该函数没有最大值
【解析】
(4) 或:该函数在 处断开;该函数没有最小值;该函数图象没有经过第四象限
【知识点】反比例函数的图象与性质、反比例函数的图象变换、二次函数的图象与性质
24. 【答案】
(1) 根据二次函数 ,对称轴 ,
系数 ,,,
又 点 ,对称轴是直线 ,
代入得:,,
则 ,,
函数解析式为 .
顶点坐标为 ,
代入 ,, 得:顶点 .
(2) 由平移知识知平移后解析式为:,
则与 正半轴交点为 ,代入函数式求得 ,即 ,
根据求得坐标作图,作 轴,
则 ,
,
代入数值解得:,即 的面积为 .
(3) 作 平行于 交抛物线于点 ,由题意设 ,
,
,
由点 ,,得:,
,,
,解得: 或 ,
在对称轴右侧,
,
,
把 代入原函数表达式得:;
点坐标为 .
【知识点】二次函数的解析式、二次函数的图象变换、基本定理、二次函数与方程、二次函数的顶点、y=ax^2+bx+c的图象
25. 【答案】
(1) 抛物线 向下平移 个单位长度得到抛物线 ,再将抛物线 向左平移 个单位长度得到抛物线 ,
抛物线 的解析式为:,即 ,
抛物线 的解析式为:,即 .
(2) 如下图,过点 作 轴于点 ,连接 ,
是等腰直角三角形,
,
又 ,
点 ,,, 四点共圆,
,
,
是等腰直角三角形,
.
点 在抛物线 对称轴 右侧上,点 在对称轴 上,
抛物线 的对称轴为 ,
设点 的坐标为 ,
,,
,
解得: 或 (舍去),
点 的坐标为 ;
同理,当点 、点 在 轴的下方时,
,
或 (舍去),
点 的坐标为 ,
综上,点 的坐标为 或 .
(3) 直线 (, 为常数)与抛物线 交于 , 两点,
,
设点 的横坐标为 ,点 的横坐标为 ,
,
中点 的横坐标 ,
中点 的纵坐标 ,
点 的坐标为 ;
同理可得:点 的坐标为 ,
设直线 的解析式为 ,
将 , 代入得:
解得:
直线 的解析式为 ,
不论 取何值时(),当 时,,
直线 经过定点 .
【知识点】二次函数的图象变换、判断四点共圆的方法、连线与坐标轴平行的两点间距离、一次函数的解析式、二次函数与方程、y=ax^2+bx+c的图象
26. 【答案】
(1) 根据有界函数的定义知,函数 不是有界函数,
是有界函数,
当 时,,
当 时,,
.
故 的边界值为 .
(2) 函数 的图象是 随 的增大而减小,
当 时,,则 ,
当 时,,则
解得:.
(3) 若 ,函数向下平移 个单位后, 时,函数值小于 ,此时函数的边界 ,与题意不符,故 .
当 时, 即过点 ,
当 时,,即过点 ,
都向下平移 个单位,则 ,,
或 ,
或 .
【知识点】反比例函数图像上的点的坐标特征、k,b对一次函数图象及性质的影响、一次函数图像上点的坐标特征、二次函数的图象变换
27. 【答案】
(1) 令 ,则 ,解得 ,,
在 的左侧,
,
令 ,则 ,即 ,
设直线 解析式为 ,把 , 代入,
解得:
直线 解析式为:.
(2) 如图 ,过 作 轴交 于点 ,
,
当 取最大值时, 最大,
设 ,,
当 时, 取最大值,此时 ,
在抛物线 中,
对称轴为 ,
由平移知直线 为:,
,
设直线 与 轴的垂足为 ,连接 ,
在 中,,,,
,
,
作 关于直线 的对称点 ,连接 ,
与直线 , 分别交于 , 点,
则 是等边三角形,
,,
,,,
,
将 沿 方向平移 个单位得到 ,
将直线 绕点 顺时针旋转 得到直线 ,
过点 作 于点 ,与 的交点即为 点,
易知 和 都为等腰直角三角形,
,,
,
.
(3) 连接 ,则 为等边三角形,
,,
,,,
①如图 ,当四边形 为矩形时,
,
由题意知, 与直线 的夹角为 ,
,
,,
,
同理可求出 ,,.
综上所述:在直角坐标平面内存在一点 ,使得以点 ,,, 为顶点的四边形是矩形,坐标是 ,,,.
【知识点】二次函数的图象与性质、二次函数的解析式、旋转及其性质
28. 【答案】
(1) 方法一:
将 和 代入方程得:,
整理得:,
解得:.
(2) 方法一:
将 代入 ,得:,
将 代入二次函数 ,
得:,则 ,
故解析式为:.
(3) 方法一:
如图:
的取值范围为: 或 .
【解析】
(1) 方法二:
在 和 时函数值相等,
代入得:,解得:.
(2) 方法二:
当 时,,
二次函数的图象与直线 的一个交点为 ,
把 代入 得:,,
二次函数的解析式是:.
(3) 方法二:
当 时,,
当 时,,解得:,
当 时,,解:,
,.
,,,,,
,,,
图象 为二次函数在 的部分,
从下端看最早相交的点为 与 相交,即 时,
从上端看, 与 相交,即 时;
由图象得:当图象 与平移后的线段有公共点时, 的取值范围是 或 .
【知识点】二次函数的图象变换、二次函数的解析式、二次函数与方程
一、选择题
将 的图象向右平移 个单位,再向下平移 个单位,所得函数的对称轴和最小值分别为
A. , B. , C. , D. ,
如图,, 分别为 图象上的两点,且直线 垂直于 轴.若 ,则直线 的解析式为
A. B. C. D.
如图为二次函数 的图象,则下列说法:① ;② ;③ ;④ 当 时,.其中正确的个数为
A. B. C. D.
已知二次函数 ( 为常数),在自变量 的值满足 的情况下,与其对应的函数值 的最小值为 ,则 的值为
A. 或 B. 或 C. 或 D. 或
二次函数 的图象如图所示,下列说法:
① ;
②当 时,;
③ ;
④若 , 在函数图象上,当 时,.
其中正确的是
A.①②④ B.①③ C.①②③ D.①③④
二次函数 的图象如图,若一元二次方程 有实数根,则 的最大值为
A. B. C. D.
如图,已知抛物线 的对称轴为直线 ,过其顶点 的一条直线 与该抛物线的另一个交点为 .若要在 轴上找一点 ,使得 最小,则点 的坐标为
A. B. C. D.
如图,抛物线 .将该抛物线在 轴和 轴下方的部分记作 ,将 沿 轴翻折记作 , 和 构成的图形记作 .关于图形 ,给出如下四个结论,其中错误的是
A.图形 恰好经过 个整点(即横、纵坐标均为整数的点)
B.图形 上任意一点到原点的距离都不超过
C.图形 的周长大于
D.图形 所围成的区域的面积大于 且小于
如图,抛物线 与 轴负半轴交于点 ,点 为线段 上一动点,点 的坐标为 ,连接 ,以 为底边向右侧作等腰直角 ,若点 恰好在抛物线上,则 长为
A. B. C. D.
如图,已知抛物线 ,把此抛物线沿 轴向上平移,平移后的抛物线和原抛物线与经过点 , 且平行于 轴的两条直线所围成的阴影部分的面积为 ,平移的距离为 ,则下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
二、填空题
如图,抛物线 与 轴的负半轴交于点 ,与 轴交于点 ,连接 ,点 , 分别是直线 与抛物线上的点,若点 ,,, 围成的四边形是平行四边形,则点 的坐标为 .
如图,在平面直角坐标系中,二次函数 的图象过正方形 的三个顶点 ,,,则 的值是 .
已知二次函数 的图象与 轴交于 和 ,其中 ,与 轴交于正半轴上一点.下列结论:① ;② ;③ ;④ .其中正确结论的序号是 .
设抛物线 ,其中 为实数.
()若抛物线经过点 ,则 ;
()将抛物线 向上平移 个单位,所得抛物线顶点的纵坐标的最大值是 .
将抛物线 向上平移 个单位长度后,经过点 ,则 的值是 .
已知抛物线 过点 ,且抛物线上任意不同两点 , 都满足:当 时,;当 时,.以原点 为圆心, 为半径的圆与抛物线的另两个交点为 ,,且 在 的左侧, 有一个内角为 ,则抛物线的解析式为 .
已知当 和 时,多项式 的值相等,且 ,则当 时,多项式 的值等于 .
如图,一段抛物线:,记为 ,它与 轴交于点 ,;将 绕点 旋转 得 ,交 轴于点 ;将 绕点 旋转 得 ,交 轴于点 ; 如此进行下去,直至得 ,若 在第 段抛物线 上,则 的值为 .
三、解答题
已知函数 与 .
(1) 完成下表:
X -3 -2 -1 0 1 2 3
Y=-(x+1)2
Y=-(x-1)2
(2) 建立平面直角坐标系,并在坐标系中作出二次函数 与 的图象;
(3) 抛物线 与 之间有什么关系?它们是轴对称图形吗?它们的对称轴和顶点坐标分别是什么?
(4) 随 的增大, 分别是如何变化的?
已知在平面直角坐标系 中,二次函数 的图象经过点 和点 .
(1) 求这个二次函数的解析式;
(2) 将这个二次函数的图象向上平移,交 轴于点 ,其纵坐标为 ,请用 的代数式表示平移后函数图象顶点 的坐标;
(3) 在第()小题的条件下,如果点 的坐标为 , 平分 ,求 的值.
有一个二次函数满足以下条件:
①函数图象与 轴的交点坐标分别为 ,(点 在点 的右侧);
②对称轴是 ;
③该函数有最小值是 .
(1) 请根据以上信息求出二次函数表达式;
(2) 将该函数图象中 部分的图象向下翻折与原图象未翻折的部分组成图象“”,试结合图象分析:平行于 轴的直线 与图象“”的交点的个数情况.
如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点,与 轴交于点 .
(1) 若点 为直线 上方抛物线上的动点,当 的面积最大时,求此时 点的坐标;
(2) 若点 是抛物线对称轴上的动点,点 是抛物线上的动点,当以点 ,,, 为顶点的四边形是平行四边形时,直接写出此时 点的坐标.
有这样一个问题:探究函数 的图象与性质.
小东根据学习函数的经验,对函数 的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1) 函数 的自变量 的取值范围是 ;
(2) 下表是 与 的几组对应值.
X ··· -3 -2 -1 - - 1 2 3 ···
Y ··· - - - m ···
求 的值;
(3) 如下图,在平面直角坐标系 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4) 进一步探究发现,该函数图象在第一象限内的最低点的坐标是 ,结合函数的图象,写出该函数的其他性质(一条即可): .
如图,在平面直角坐标系 中,已知抛物线 经过点 ,对称轴是直线 ,顶点为点 ,抛物线与 轴交于点 .
(1) 求抛物线的表达式和点 的坐标;
(2) 将上述抛物线向下平移 个单位,平移后的抛物线与 轴正半轴交于点 ,求 的面积;
(3) 如果点 在原抛物线上,且在对称轴的右侧,连接 交线段 于点 ,,求点 的坐标.
将抛物线 向下平移 个单位长度得到抛物线 ,再将抛物线 向左平移 个单位长度得到抛物线 .
(1) 直接写出抛物线 , 的解析式;
(2) 如图(),点 在抛物线 对称轴 右侧上,点 在对称轴 上, 是以 为斜边的等腰直角三角形,求点 的坐标;
(3) 如图(),直线 (, 为常数)与抛物线 交于 , 两点, 为线段 的中点;直线 与抛物线 交于 , 两点, 为线段 的中点.求证:直线 经过一个定点.
对某一个函数给出如下定义:若存在实数 ,对于任意的函数值 ,都满足 ,则称这个函数是有界函数,在所有满足条件的 中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是 .
(1) 分别判断函数 和 是不是有界函数.若是有界函数,求其边界值.
(2) 若函数 (,)的边界值是 ,且这个函数的最大值也是 ,求 的取值范围.
(3) 将函数 (,)的图象向下平移 个单位,得到的函数的边界值是 ,当 在什么范围时,满足 .
如图 ,抛物线 与 轴交于 ,( 在 的左侧)两点,与 轴交于点 ,将直线 沿 轴正方向平移 个单位得到直线 ,将抛物线的对称轴沿 轴正方向平移 个单位得到直线 .
(1) 求直线 的解析式;
(2) 如图 ,点 为直线 上方抛物线上一动点,连接 , 与直线 分别交于点 ,,过点 作 于点 , 是线段 上一动点,过 作 于点 ,连接 ,当 的面积最大时,求 的最小值;
(3) 如图 ,连接 ,将 绕点 顺时针旋转 后得到 ,点 是直线 上一点,在直角坐标平面内是否存在一点 ,使得以点 ,,, 为顶点的四边形是矩形?若存在,求出点 的坐标;若不存在,请说明理由.
已知关于 的二次函数 在 和 时函数值相等.
(1) 求 的值.
(2) 若该二次函数的图象与直线 的一个交点为 ,求它的解析式.
(3) 在()的条件下,直线 与 轴, 轴分别交于点 ,,将线段 向右平移 个单位,同时将该二次函数在 的部分向左平移 个单位后得到的图象记为 ,请结合图象回答,当图象 与平移后的线段有公共点时, 的取值范围.
答案
一、选择题
1. 【答案】A
【解析】将 的图象向右平移 个单位,再向下平移 个单位,
所得图象的函数表达式是 即 ,
所以对称轴为 ,最小值为 .
【知识点】二次函数的图象变换、二次函数的图象与性质
2. 【答案】C
【知识点】二次函数的图象与性质、一次函数的解析式
3. 【答案】C
【解析】①开口向下,故 ,①错误;
②对称轴为直线 ,故 ,,,②正确;
③当 时,,③正确
④由图得,当 时,,④正确.
【知识点】二次函数的图象与性质
4. 【答案】B
【解析】二次函数的对称轴为直线 ,以下分情况讨论.
当 时,当 时, 取得最小值,即 ,解得 ,(舍去);
当 时,当 时, 取得最小值 ,不符合题意;
当 时,当 时, 取得最小值,即 ,解得 ,(舍去).
综上所述,.
【知识点】二次函数的最值
5. 【答案】B
【解析】 函数图象的对称轴为:,
,即 ,①正确;
由图象可知,当 时,,②错误;
由图象可知,当 时,,
,
,
,③正确;
抛物线的对称轴为 ,开口方向向上,
若 , 在函数图象上,
当 时,;当 时,,
故④错误.
【知识点】二次函数的图象与性质
6. 【答案】B
【解析】提示:令 ,则 是由二次函数 向上平移 个单位得到的函数,由图象可知二次函数 向上平移三个单位后与 轴只有一个交点,再向上平移没有交点,所以 的最大值为 .
【知识点】二次函数的图象与性质
7. 【答案】B
【解析】如图,作 点关于 轴的对称点 ,连接 交 轴于 点.
将 点坐标代入抛物线,并联立对称轴,
得 解得
,
, 点关于 轴的对称点 ,
设 的解析式为 ,
将 , 代入函数解析式,
得 解得
的解析式为 ,
当 时,,即 .
【知识点】轴对称之最短路径、二次函数的图象与性质、一次函数的解析式
8. 【答案】C
【知识点】二次函数的图象变换
9. 【答案】C
【解析】由题意,作 轴,,垂足分别为 ,.
设 点坐标为 ,
则 ,,
为等腰直角三角形,
,,
,
,
,
在 与 中,
,
,
,
,,(舍去),
,,
,
,
,
,
,
.
【知识点】二次函数的图象与性质、角角边
10. 【答案】B
【解析】如图,作出抛物线的对称轴 .
因为抛物线是上下平移,所以两个抛物线是同一条对称轴.
设对称轴与两抛物线分别交于 、 两点,直线 与抛物线交于 、 ,直线 与抛物线交于 、 ,则 ,
所以阴影部分的面积等于两个平行四边形的面积之和,即 .
【知识点】平行四边形、函数关系的表示、二次函数的图象变换
二、填空题
11. 【答案】 或 或
【解析】 抛物线 与 轴的负半轴交于点 ,与 轴交于点 ,
,.
当 为平行四边形的边时,,且 ,
线段 可由线段 平移得到.
点 在直线 上,
①当点 的对应点为 时,如图,
需先将 向左平移 个单位长度,此时点 的对应点 的横坐标为 ,
将 代入 ,得 ,
.
②当点 的对应点为 时,
同理,先将 向右平移 个单位长度,可得点 的对应点 的横坐标为 ,
将 代入 ,得 ,
;
当 为平行四边形的对角线时,可知 的中点坐标为 ,
在直线 上,
根据对称性可知 的横坐标为 ,
将 代入 ,得 ,
.
综上所述,点 的坐标为 或 或 .
【知识点】平行四边形的判定、二次函数的图象与性质、二次函数与方程
12. 【答案】
【知识点】二次函数的图象与性质、勾股定理、正方形的性质
13. 【答案】②④
【解析】 抛物线与x轴的交点为 和 ,,与 轴交于正半轴,
.
,
.
,,故①错误,③错误;
抛物线与 轴有两个交点,
.
,故②正确;
抛物线与 轴的交点有一个为 ,
.
.
,(已证),
,.
,,
,故④正确.
【知识点】二次函数的图象与性质
14. 【答案】 ;
【解析】()点 代入抛物线解析式 ,
得 ,解得 .
() 向上平移 个单位可得,,
所以 ,
所以抛物线顶点的纵坐标 ,
因为 ,
所以 的最大值为 .
【知识点】二次函数图像上点的坐标特征、二次函数的图象变换、二次函数的顶点
15. 【答案】
【解析】将抛物线 向上平移 个单位长度后,
表达式为:,
经过点 ,代入得:,
则 .
【知识点】二次函数的图象变换
16. 【答案】
【解析】 抛物线过点 ,
,
当 时,,由 ,得到 ,
当 时, 随 的增大而增大,
同理当 时, 随 的增大而减小,
抛物线的对称轴为 轴,且开口向下,即 ,
以 为圆心, 为半径的圆与抛物线交于另两点 ,,如图所示,
为等腰三角形,
中有一个角为 ,
为等边三角形,且 ,
设线段 与 轴的交点为点 ,则有 ,且 ,
,,
在 的左侧,
的坐标为 ,
点在抛物线上,且 ,,
,
解得:,
则抛物线解析式为 .
【知识点】解直角三角形、二次函数的图象与性质、圆的对称性
17. 【答案】
【解析】 和 时,多项式 的值相等,
二次函数 的对称轴为直线 ,
二次函数 的对称轴为直线 ,
,
,,
当 时,.
【知识点】二次函数的图象与性质
18. 【答案】
【解析】令 ,则 ,解得 ,,
,
由图可知,抛物线 在 轴下方,
相当于抛物线 向右平移 个单位得到 ,
再将 绕点 旋转 得 ,
抛物线 解析式为 ,
在第 段抛物线 上,
.
【知识点】二次函数的图象变换
三、解答题
19. 【答案】
(1) 略
(2) 略
(3) 抛物线 和 都可以看作是由 平移得到的,即它们的开口方向相同、开口大小相同,形状相同.它们是轴对称图形,它们的对称轴分别是直线 ,,顶点坐标分别是 ,.
(4) 二次函数 : 时, 随 增大而减小, 时, 随 增大而增大;二次函数 : 时, 随 增大而减小, 时, 随 增大而增大.
【知识点】描点法画二次函数图像、y=a(x-h)^2的图象、二次函数的增减性、二次函数的图象变换
20. 【答案】
(1) .
(2) .
(3) .
【知识点】二次函数的解析式、角平分线的性质、二次函数的顶点、二次函数的图象变换、二次函数与方程、坐标平面内图形轴对称变换
21. 【答案】
(1) 由上述信息可知该函数图象的顶点坐标为 ,
设二次函数的表达式为 .
该函数图象经过点 ,
,解得 .
二次函数解析式为 .
(2) 如图所示.
当 时,直线 与 有一个交点;
当 时,直线 与 有两个交点;
当 时,直线 与 有三个交点;
当 时,直线 与 有两个交点;
当 时,直线 与 有一个交点.
【知识点】二次函数的图象变换、二次函数的解析式
22. 【答案】
(1) 抛物线 与 轴交于 , 两点,
,
,,
点 的坐标为 ,点 的坐标为 ,
抛物线 与 轴交于点 ,
点 的坐标为 ,
点 的坐标为 ,点 的坐标为 ,
直线 解析式为:.
如图,过点 作 ,交 于点 ,
设点 ,则点 ,
,
的面积 ,
当 时, 的面积有最大值,
点 .
(2) 点 的坐标为 或 或 .
【解析】
(2) 设点 坐标为 ,
点 的坐标为 ,点 的坐标为 ,
抛物线的对称轴为直线 ,
点 是抛物线对称轴上的动点,
设点 坐标为 ,
当 为边时,则四边形 是平行四边形或四边形 是平行四边形,
若四边形 是平行四边形,
与 互相平分,
,,
,,
,
,
点 坐标为 ;
若四边形 是平行四边形,
与 互相平分,
,,
,,
,
,
点 坐标为 ;
当 为对角线时,
以点 ,,, 为顶点的四边形是平行四边形,
与 是互相平分,
,,
,,
,
,
点 坐标为 .
综上所述:点 的坐标为 或 或 .
【知识点】二次函数的图象与性质、平行四边形的判定、二次函数与方程
23. 【答案】
(1)
(2) 令 ,
,
.
(3) 如图,
(4) 该函数没有最大值
【解析】
(4) 或:该函数在 处断开;该函数没有最小值;该函数图象没有经过第四象限
【知识点】反比例函数的图象与性质、反比例函数的图象变换、二次函数的图象与性质
24. 【答案】
(1) 根据二次函数 ,对称轴 ,
系数 ,,,
又 点 ,对称轴是直线 ,
代入得:,,
则 ,,
函数解析式为 .
顶点坐标为 ,
代入 ,, 得:顶点 .
(2) 由平移知识知平移后解析式为:,
则与 正半轴交点为 ,代入函数式求得 ,即 ,
根据求得坐标作图,作 轴,
则 ,
,
代入数值解得:,即 的面积为 .
(3) 作 平行于 交抛物线于点 ,由题意设 ,
,
,
由点 ,,得:,
,,
,解得: 或 ,
在对称轴右侧,
,
,
把 代入原函数表达式得:;
点坐标为 .
【知识点】二次函数的解析式、二次函数的图象变换、基本定理、二次函数与方程、二次函数的顶点、y=ax^2+bx+c的图象
25. 【答案】
(1) 抛物线 向下平移 个单位长度得到抛物线 ,再将抛物线 向左平移 个单位长度得到抛物线 ,
抛物线 的解析式为:,即 ,
抛物线 的解析式为:,即 .
(2) 如下图,过点 作 轴于点 ,连接 ,
是等腰直角三角形,
,
又 ,
点 ,,, 四点共圆,
,
,
是等腰直角三角形,
.
点 在抛物线 对称轴 右侧上,点 在对称轴 上,
抛物线 的对称轴为 ,
设点 的坐标为 ,
,,
,
解得: 或 (舍去),
点 的坐标为 ;
同理,当点 、点 在 轴的下方时,
,
或 (舍去),
点 的坐标为 ,
综上,点 的坐标为 或 .
(3) 直线 (, 为常数)与抛物线 交于 , 两点,
,
设点 的横坐标为 ,点 的横坐标为 ,
,
中点 的横坐标 ,
中点 的纵坐标 ,
点 的坐标为 ;
同理可得:点 的坐标为 ,
设直线 的解析式为 ,
将 , 代入得:
解得:
直线 的解析式为 ,
不论 取何值时(),当 时,,
直线 经过定点 .
【知识点】二次函数的图象变换、判断四点共圆的方法、连线与坐标轴平行的两点间距离、一次函数的解析式、二次函数与方程、y=ax^2+bx+c的图象
26. 【答案】
(1) 根据有界函数的定义知,函数 不是有界函数,
是有界函数,
当 时,,
当 时,,
.
故 的边界值为 .
(2) 函数 的图象是 随 的增大而减小,
当 时,,则 ,
当 时,,则
解得:.
(3) 若 ,函数向下平移 个单位后, 时,函数值小于 ,此时函数的边界 ,与题意不符,故 .
当 时, 即过点 ,
当 时,,即过点 ,
都向下平移 个单位,则 ,,
或 ,
或 .
【知识点】反比例函数图像上的点的坐标特征、k,b对一次函数图象及性质的影响、一次函数图像上点的坐标特征、二次函数的图象变换
27. 【答案】
(1) 令 ,则 ,解得 ,,
在 的左侧,
,
令 ,则 ,即 ,
设直线 解析式为 ,把 , 代入,
解得:
直线 解析式为:.
(2) 如图 ,过 作 轴交 于点 ,
,
当 取最大值时, 最大,
设 ,,
当 时, 取最大值,此时 ,
在抛物线 中,
对称轴为 ,
由平移知直线 为:,
,
设直线 与 轴的垂足为 ,连接 ,
在 中,,,,
,
,
作 关于直线 的对称点 ,连接 ,
与直线 , 分别交于 , 点,
则 是等边三角形,
,,
,,,
,
将 沿 方向平移 个单位得到 ,
将直线 绕点 顺时针旋转 得到直线 ,
过点 作 于点 ,与 的交点即为 点,
易知 和 都为等腰直角三角形,
,,
,
.
(3) 连接 ,则 为等边三角形,
,,
,,,
①如图 ,当四边形 为矩形时,
,
由题意知, 与直线 的夹角为 ,
,
,,
,
同理可求出 ,,.
综上所述:在直角坐标平面内存在一点 ,使得以点 ,,, 为顶点的四边形是矩形,坐标是 ,,,.
【知识点】二次函数的图象与性质、二次函数的解析式、旋转及其性质
28. 【答案】
(1) 方法一:
将 和 代入方程得:,
整理得:,
解得:.
(2) 方法一:
将 代入 ,得:,
将 代入二次函数 ,
得:,则 ,
故解析式为:.
(3) 方法一:
如图:
的取值范围为: 或 .
【解析】
(1) 方法二:
在 和 时函数值相等,
代入得:,解得:.
(2) 方法二:
当 时,,
二次函数的图象与直线 的一个交点为 ,
把 代入 得:,,
二次函数的解析式是:.
(3) 方法二:
当 时,,
当 时,,解得:,
当 时,,解:,
,.
,,,,,
,,,
图象 为二次函数在 的部分,
从下端看最早相交的点为 与 相交,即 时,
从上端看, 与 相交,即 时;
由图象得:当图象 与平移后的线段有公共点时, 的取值范围是 或 .
【知识点】二次函数的图象变换、二次函数的解析式、二次函数与方程
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
