2021-2022学年华东师大版七年级数学上册第四章 图形的初步认识单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版七年级数学上册第四章 图形的初步认识单元测试卷(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 303.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览




文档简介
第四章图形的初步认识同步测试卷 2021-2022学年华东师大版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共14小题,共42分)
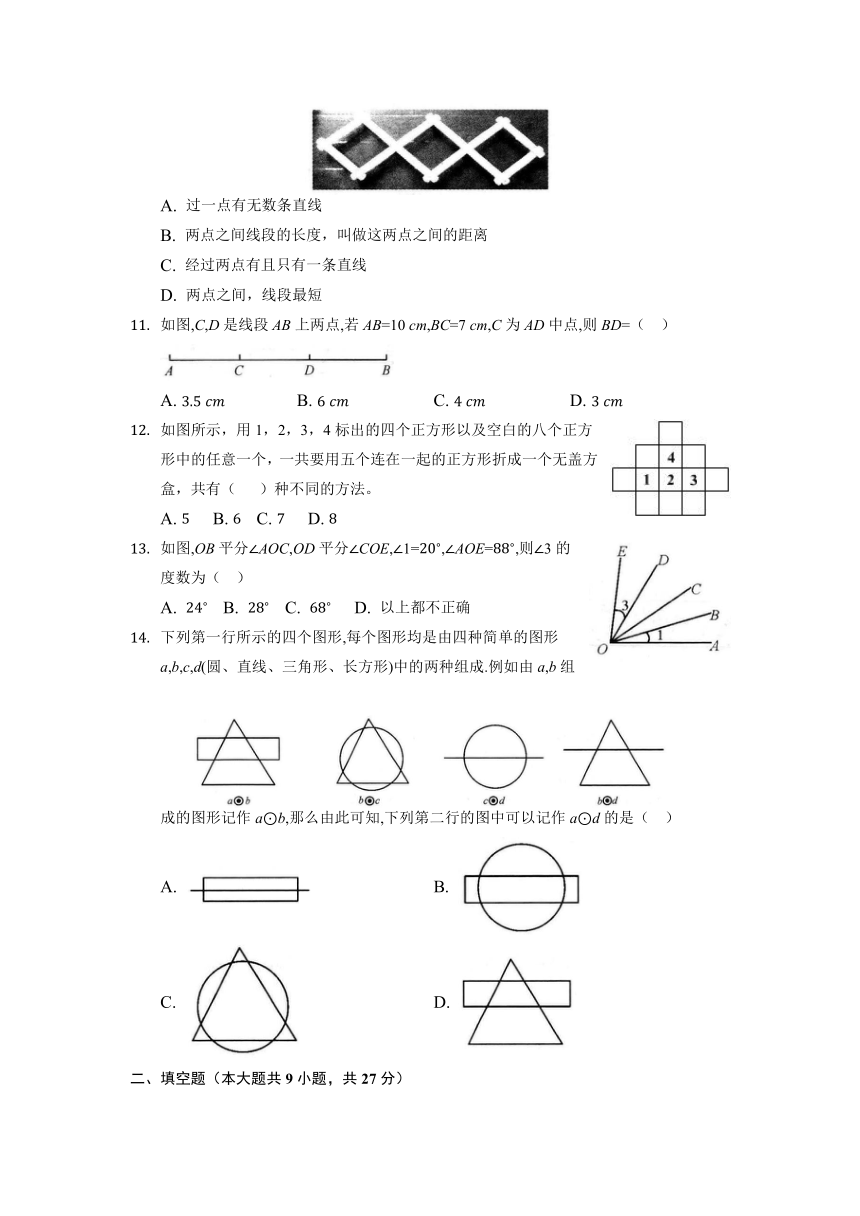
如图,给出的直线、射线、线段,根据各自的性质,能相交的是( )
A. B.
C. D.
如图,下列表示角的方法错误的是( )
A. 与表示同一个角
B. 表示的是
C. 图中共有三个角:,,
D. 也可用来表示
如图是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
A. 大 B. 伟 C. 国 D. 的
如图,下列说法中正确的是( )
A. 的方向是北偏东
B. 的方向是北偏西
C. 的方向是南偏西
D. 的方向是东南方向
如图,下列七个图形是正方体的展开图的有( )
A. 个 B. 个 C. 个 D. 个
有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图所示),请你根据图形判断涂成绿色一面的对面的颜色是().
A. 白 B. 红 C. 黄 D. 黑
如图所示为一无盖长方体盒子的表面展开图(重叠部分不计),可知该无盖长方体的容积为().
A. B. C. D.
下列图形不是立体图形的是( )
A. 球 B. 圆柱 C. 圆锥 D. 圆
下列图形的主视图与其他三个不同的是( )
A. B.
C. D.
如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是( )
A. 过一点有无数条直线
B. 两点之间线段的长度,叫做这两点之间的距离
C. 经过两点有且只有一条直线
D. 两点之间,线段最短
如图,C,D是线段AB上两点,若AB=10 cm,BC=7 cm,C为AD中点,则BD=( )
A. B. C. D.
如图所示,用1,2,3,4标出的四个正方形以及空白的八个正方形中的任意一个,一共要用五个连在一起的正方形折成一个无盖方盒,共有( )种不同的方法。
A. B. C. D.
如图,OB平分AOC,OD平分COE,1=,AOE=,则3的度数为( )
A. B. C. D. 以上都不正确
下列第一行所示的四个图形,每个图形均是由四种简单的图形a,b,c,d(圆、直线、三角形、长方形)中的两种组成.例如由a,b组成的图形记作a⊙b,那么由此可知,下列第二行的图中可以记作a⊙d的是( )
A. B.
C. D.
二、填空题(本大题共9小题,共27分)
计算:-= .
如图,纸上有10个小正方形(其中5个有阴影,5个无阴影),从图中5个无阴影的小正方形中选出一个,与5个有阴影的小正方形折出一个正方体的包装盒,不同的选法有______种.
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,可以剪去________(填序号).
如果按图中虚线对折可以做成一个顶面为无盖的盒子,那么该盒子的下底面的字母是________.
如图所示,每个正方体的6个面上分别写有1到6这六个自然数,并且任意两个相对面上所写两个数字之和为7,把这样的7个正方体一个挨着一个地连接起来,叠合在一起的两个面上的数字之和为8,则图中*所在面上的数字是________.
若1与2互补,3与互余,2+3=,则1= .
如图,C,D是线段AB上的两点,若AC=4,CD=5,DB=3,则图中所有线段的和是 .
如图,将三个同样的正方形的一个顶点重合放置,那么1的度数为 .
两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,,那么六条直线最多有 个交点.
三、解答题(本大题共9小题,共51分)
如图所示为一个长方体的表面展开图,将它折叠成一个长方体,那么:
(1)与字母N重合的点是哪几个?
(2)若AG=CK=14 cm,LK=5 cm,则该长方体的表面积和体积分别是多少?
下面都是由五个相同的小正方形组成的图形,请你在各图中分别添加一个小正方形,使它们能折叠成小正方体.
如图,已知四点A,B,C,D,请用尺规作图完成.(保留画图痕迹)
(1)画直线AB;
(2)画射线AC;
(3)连结BC并延长BC到E,使得CE=AB+BC;
(4)在线段BD上取点P,使PA+PC的值最小.
如图,线段CD=2厘米,点C是AB的中点,点D是AC的中点,求线段BD的长.
如图,点C是线段AB的中点.
(1)若点D在CB上,且DB=1.5 cm,AD=6.5 cm,求线段CD的长度;
(2)若将(1)中的“点D在CB上”改为“点D在CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
如图,已知直线AB与CD相交于点O,COE=,OF平分BOE,AOC=EOF.
(1)求AOC的度数;
(2)写出图中EOF的余角和补角.
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东,射线OC的方向是北偏东,且的角与的角互余.
(1)若m=50,则射线OC的方向是 ;
图中与BOE互余的角有 ,与BOE互补的角有 ;
(2)若射线OA是BON的平分线,则BOS与AOC是否存在确定的数量关系 如果存在,请写出你的结论以及计算过程;如果不存在,请说明理由.
问题发现:
(1)如图1,已知线段AB=6,C是AB延长线上一点,D,E分别是AC,BC的中点.
若BC=4,则DE= ;
若BC=8,则DE= ;
通过以上计算,你能发现AB与DE之间的数量关系吗 直接写出结果: .
应用:(2)如图2,AOB=,OD平分AOC,OE平分BOC,求DOE的大小,并写出推导过程.
如图中a,b,c,d四个图都称作平面图形,观察图b和表中对应数值,探究计数的方法并作答.
(1)数一数每个图各有多少个顶点、多少条边,这些边围出多少个区域,并将结果填入下表(其中b已填好):
图 a b c d
顶点数(V) 7
边数(E) 9
区域数(F) 3
(2)根据表中数值,写出平面图形的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图形有20个顶点和11个区域,那么利用(2)中得出的关系,这个平面图形有多少条边
参考答案
1.【答案】D
2.【答案】D
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】C
11.【答案】C
12.【答案】B
13.【答案】A
14.【答案】A
15.【答案】
16.【答案】2
17.【答案】1或2或6
18.【答案】B
19.【答案】3
20.【答案】
21.【答案】41
22.【答案】
23.【答案】15
24.【答案】解:(1)与字母N重合的点有H,J两个;
(2)由AG=CK=14 cm,LK=5cm,
可得CL=CK-LK=14-5=9(cm),,
长方体的表面积为2×(9×5+2×5+2×9)=146(cm2),
长方体的体积为5×9×2=90(cm3).
25.【答案】解:如图.
26.【答案】解:如图.
27.【答案】解:因为点D是AC的中点,CD=2厘米,
所以AC=2CD=4厘米.
又因为点C是AB的中点,
所以CB=AC=4厘米.
所以BD=CB+CD=6厘米.
28.【答案】解:(1)AB=AD+DB=6.5+1.5=8(cm),
因为点C是线段AB的中点,
所以CB=AB=4 cm.
所以CD=CB-DB=4-1.5=2.5(cm).
(2)如图:
因为AB=AD-DB=6.5-1.5=5(cm),
所以CB=AB=2.5 cm.
所以CD=CB+DB=4 cm.
29.【答案】解:(1)因为COE=,
所以AOC+EOF+BOF=.
因为OF平分BOE,
所以EOF=BOF.
因为AOC=EOF,
所以AOC=EOF=BOF=.
(2)EOF的余角:BOE,DOF.
EOF的补角:BOC,AOF,AOD.
30.【答案】解:(1)北偏东;
BOS,EOC;BOW,COS;
(2)AOC=BOS.
因为射线OA是BON的平分线,
所以NOA=BON.
因为BOS+BON=,
所以BON=-BOS.
所以NOA=BON=-BOS.
因为NOC+BOS=,
所以NOC=-BOS.
所以AOC=NOA-NOC=-BOS-(-BOS)=BOS.
31.【答案】解:(1)3;
3;
DE=AB;
(2)因为OD平分AOC,OE平分BOC,
所以DOC=AOC,EOC=BOC.
所以DOE=DOC-EOC=(AOC-BOC)=AOB=.
32.【答案】解:(1)
图 a b c d
顶点数(V) 4 7 8 10
边数(E) 6 9 12 15
区域数(F) 3 3 5 6
(2)V+F-E=1.
(3)这个平面图形的边有20+11-1=30(条).
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共14小题,共42分)
如图,给出的直线、射线、线段,根据各自的性质,能相交的是( )
A. B.
C. D.
如图,下列表示角的方法错误的是( )
A. 与表示同一个角
B. 表示的是
C. 图中共有三个角:,,
D. 也可用来表示
如图是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
A. 大 B. 伟 C. 国 D. 的
如图,下列说法中正确的是( )
A. 的方向是北偏东
B. 的方向是北偏西
C. 的方向是南偏西
D. 的方向是东南方向
如图,下列七个图形是正方体的展开图的有( )
A. 个 B. 个 C. 个 D. 个
有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图所示),请你根据图形判断涂成绿色一面的对面的颜色是().
A. 白 B. 红 C. 黄 D. 黑
如图所示为一无盖长方体盒子的表面展开图(重叠部分不计),可知该无盖长方体的容积为().
A. B. C. D.
下列图形不是立体图形的是( )
A. 球 B. 圆柱 C. 圆锥 D. 圆
下列图形的主视图与其他三个不同的是( )
A. B.
C. D.
如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是( )
A. 过一点有无数条直线
B. 两点之间线段的长度,叫做这两点之间的距离
C. 经过两点有且只有一条直线
D. 两点之间,线段最短
如图,C,D是线段AB上两点,若AB=10 cm,BC=7 cm,C为AD中点,则BD=( )
A. B. C. D.
如图所示,用1,2,3,4标出的四个正方形以及空白的八个正方形中的任意一个,一共要用五个连在一起的正方形折成一个无盖方盒,共有( )种不同的方法。
A. B. C. D.
如图,OB平分AOC,OD平分COE,1=,AOE=,则3的度数为( )
A. B. C. D. 以上都不正确
下列第一行所示的四个图形,每个图形均是由四种简单的图形a,b,c,d(圆、直线、三角形、长方形)中的两种组成.例如由a,b组成的图形记作a⊙b,那么由此可知,下列第二行的图中可以记作a⊙d的是( )
A. B.
C. D.
二、填空题(本大题共9小题,共27分)
计算:-= .
如图,纸上有10个小正方形(其中5个有阴影,5个无阴影),从图中5个无阴影的小正方形中选出一个,与5个有阴影的小正方形折出一个正方体的包装盒,不同的选法有______种.
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,可以剪去________(填序号).
如果按图中虚线对折可以做成一个顶面为无盖的盒子,那么该盒子的下底面的字母是________.
如图所示,每个正方体的6个面上分别写有1到6这六个自然数,并且任意两个相对面上所写两个数字之和为7,把这样的7个正方体一个挨着一个地连接起来,叠合在一起的两个面上的数字之和为8,则图中*所在面上的数字是________.
若1与2互补,3与互余,2+3=,则1= .
如图,C,D是线段AB上的两点,若AC=4,CD=5,DB=3,则图中所有线段的和是 .
如图,将三个同样的正方形的一个顶点重合放置,那么1的度数为 .
两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,,那么六条直线最多有 个交点.
三、解答题(本大题共9小题,共51分)
如图所示为一个长方体的表面展开图,将它折叠成一个长方体,那么:
(1)与字母N重合的点是哪几个?
(2)若AG=CK=14 cm,LK=5 cm,则该长方体的表面积和体积分别是多少?
下面都是由五个相同的小正方形组成的图形,请你在各图中分别添加一个小正方形,使它们能折叠成小正方体.
如图,已知四点A,B,C,D,请用尺规作图完成.(保留画图痕迹)
(1)画直线AB;
(2)画射线AC;
(3)连结BC并延长BC到E,使得CE=AB+BC;
(4)在线段BD上取点P,使PA+PC的值最小.
如图,线段CD=2厘米,点C是AB的中点,点D是AC的中点,求线段BD的长.
如图,点C是线段AB的中点.
(1)若点D在CB上,且DB=1.5 cm,AD=6.5 cm,求线段CD的长度;
(2)若将(1)中的“点D在CB上”改为“点D在CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
如图,已知直线AB与CD相交于点O,COE=,OF平分BOE,AOC=EOF.
(1)求AOC的度数;
(2)写出图中EOF的余角和补角.
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东,射线OC的方向是北偏东,且的角与的角互余.
(1)若m=50,则射线OC的方向是 ;
图中与BOE互余的角有 ,与BOE互补的角有 ;
(2)若射线OA是BON的平分线,则BOS与AOC是否存在确定的数量关系 如果存在,请写出你的结论以及计算过程;如果不存在,请说明理由.
问题发现:
(1)如图1,已知线段AB=6,C是AB延长线上一点,D,E分别是AC,BC的中点.
若BC=4,则DE= ;
若BC=8,则DE= ;
通过以上计算,你能发现AB与DE之间的数量关系吗 直接写出结果: .
应用:(2)如图2,AOB=,OD平分AOC,OE平分BOC,求DOE的大小,并写出推导过程.
如图中a,b,c,d四个图都称作平面图形,观察图b和表中对应数值,探究计数的方法并作答.
(1)数一数每个图各有多少个顶点、多少条边,这些边围出多少个区域,并将结果填入下表(其中b已填好):
图 a b c d
顶点数(V) 7
边数(E) 9
区域数(F) 3
(2)根据表中数值,写出平面图形的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图形有20个顶点和11个区域,那么利用(2)中得出的关系,这个平面图形有多少条边
参考答案
1.【答案】D
2.【答案】D
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】C
11.【答案】C
12.【答案】B
13.【答案】A
14.【答案】A
15.【答案】
16.【答案】2
17.【答案】1或2或6
18.【答案】B
19.【答案】3
20.【答案】
21.【答案】41
22.【答案】
23.【答案】15
24.【答案】解:(1)与字母N重合的点有H,J两个;
(2)由AG=CK=14 cm,LK=5cm,
可得CL=CK-LK=14-5=9(cm),,
长方体的表面积为2×(9×5+2×5+2×9)=146(cm2),
长方体的体积为5×9×2=90(cm3).
25.【答案】解:如图.
26.【答案】解:如图.
27.【答案】解:因为点D是AC的中点,CD=2厘米,
所以AC=2CD=4厘米.
又因为点C是AB的中点,
所以CB=AC=4厘米.
所以BD=CB+CD=6厘米.
28.【答案】解:(1)AB=AD+DB=6.5+1.5=8(cm),
因为点C是线段AB的中点,
所以CB=AB=4 cm.
所以CD=CB-DB=4-1.5=2.5(cm).
(2)如图:
因为AB=AD-DB=6.5-1.5=5(cm),
所以CB=AB=2.5 cm.
所以CD=CB+DB=4 cm.
29.【答案】解:(1)因为COE=,
所以AOC+EOF+BOF=.
因为OF平分BOE,
所以EOF=BOF.
因为AOC=EOF,
所以AOC=EOF=BOF=.
(2)EOF的余角:BOE,DOF.
EOF的补角:BOC,AOF,AOD.
30.【答案】解:(1)北偏东;
BOS,EOC;BOW,COS;
(2)AOC=BOS.
因为射线OA是BON的平分线,
所以NOA=BON.
因为BOS+BON=,
所以BON=-BOS.
所以NOA=BON=-BOS.
因为NOC+BOS=,
所以NOC=-BOS.
所以AOC=NOA-NOC=-BOS-(-BOS)=BOS.
31.【答案】解:(1)3;
3;
DE=AB;
(2)因为OD平分AOC,OE平分BOC,
所以DOC=AOC,EOC=BOC.
所以DOE=DOC-EOC=(AOC-BOC)=AOB=.
32.【答案】解:(1)
图 a b c d
顶点数(V) 4 7 8 10
边数(E) 6 9 12 15
区域数(F) 3 3 5 6
(2)V+F-E=1.
(3)这个平面图形的边有20+11-1=30(条).
第2页,共3页
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
