人教版2021-2022学年九年级数学上册23.2.2 中心对称图形 课后练习(word版、含答案)
文档属性
| 名称 | 人教版2021-2022学年九年级数学上册23.2.2 中心对称图形 课后练习(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 565.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览



文档简介
2021——2022学年度人教版九年级数学上册 第二十三章 旋转 23.2.2 中心对称图形 课后练习
一、选择题
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.下面的图形是用数学家名字命名的,其中是轴对称图形,但不是中心对称图形的是( )
A.科克曲线 B.笛卡尔心形线
C.赵爽弦图 D.斐波那契螺旋线
3.下列命题:①顺次连接菱形各边中点得到的四边形是矩形;②平行四边形既是中心对称图形又是轴对称图形;③的算术平方根是3;④对于任意实数m,关于x的方程有两个不相等的实数根.其中正确的命题个数是( )
A.1个 B.2个 C.3个 D.4个
4.下列图形中,是中心对称图形但不是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
5.如图所示的两个三角形(B、F、C、E四点共线)是中心对称图形,则对称中心是( )
A.点C B.点D
C.线段BC的中点 D.线段FC的中点
6.下列说法中,正确的是( )
A.形状和大小完全相同的两个图形成中心对称
B.成中心对称的两个图形必重合
C.成中心对称的两个图形形状和大小完全相同
D.旋转后能重合的两个图形成中心对称
7.如图,和关于点成中心对称,则点坐标是( )
A. B. C. D.
8.如图是的网格图,将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
A.① B.② C.③ D.④
9.如图,在4×4的网格纸中,ABC的三个顶点都在格点上,现要在这张网格纸的四个格点M,N,P,Q中找一点作为旋转中心.将ABC绕着这个中心进行旋转,旋转前后的两个三角形成中心对称,且旋转后的三角形的三个顶点都在这张4×4的网格纸的格点上,那么满足条件的旋转中心有( )
A.点M,点N B.点M,点Q C.点N,点P D.点P,点Q
10.若两个图形成中心对称,则下列说法:
①对应点的连线必经过对称中心;②这两个图形的形状和大小完全相同;
③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转某个角度后必与另一个图形重合.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.给出下列5种图形:①平行四边形②菱形③正五边形、④正六边形、⑤等腰梯形中,既是轴对称又是中心对称的图形有________个.
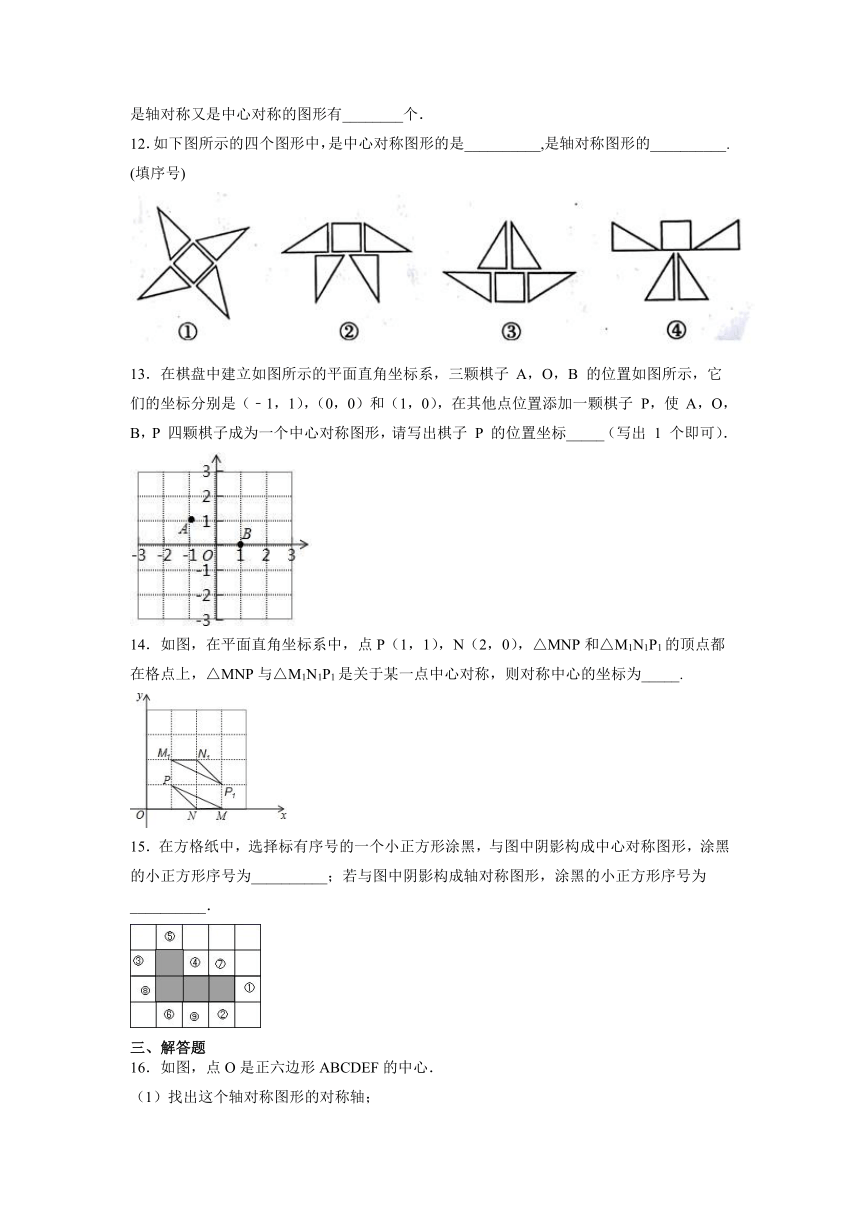
12.如下图所示的四个图形中,是中心对称图形的是__________,是轴对称图形的__________. (填序号)
13.在棋盘中建立如图所示的平面直角坐标系,三颗棋子 A,O,B 的位置如图所示,它们的坐标分别是(﹣1,1),(0,0)和(1,0),在其他点位置添加一颗棋子 P,使 A,O,B,P 四颗棋子成为一个中心对称图形,请写出棋子 P 的位置坐标_____(写出 1 个即可).
14.如图,在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为_____.
15.在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影构成中心对称图形,涂黑的小正方形序号为__________;若与图中阴影构成轴对称图形,涂黑的小正方形序号为__________.
三、解答题
16.如图,点O是正六边形ABCDEF的中心.
(1)找出这个轴对称图形的对称轴;
(2)这个正六边形绕点O旋转多少度后能和原来的图形重合?
(3)如果换成其他的正多边形呢?能得到一般的结论吗?
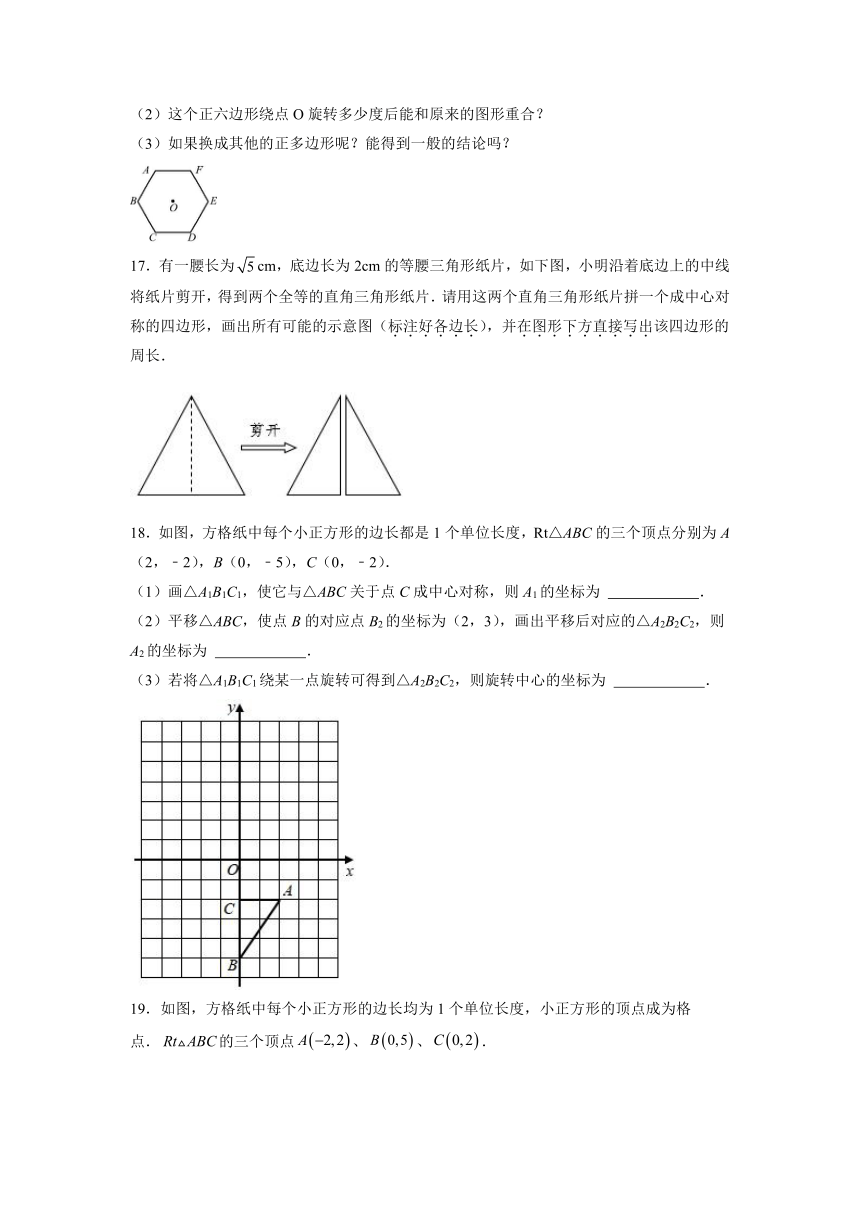
17.有一腰长为cm,底边长为2cm的等腰三角形纸片,如下图,小明沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片.请用这两个直角三角形纸片拼一个成中心对称的四边形,画出所有可能的示意图(标注好各边长),并在图形下方直接写出该四边形的周长.
18.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(2,﹣2),B(0,﹣5),C(0,﹣2).
(1)画△A1B1C1,使它与△ABC关于点C成中心对称,则A1的坐标为 .
(2)平移△ABC,使点B的对应点B2的坐标为(2,3),画出平移后对应的△A2B2C2,则A2的坐标为 .
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,则旋转中心的坐标为 .
19.如图,方格纸中每个小正方形的边长均为1个单位长度,小正方形的顶点成为格点.的三个顶点、、.
(1)将以点C为旋转中心旋转180°,得到,画出,并直接写出点、的坐标;
(2)平移,使点A的对应点为,请画出平移后对应的;
(3)若将绕某一点旋转可得到,请直接写出旋转中心的坐标.
20.如图,在网格图中建立平面直角坐标系,的顶点坐标为、、.
(1)若将向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的;
(2)画出绕C1顺时针方向旋转90°后得到的;
(3)与是中心对称图形,请写出对称中心的坐标: ;并计算的面积: .
21.在学习函数的过程中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=ax3﹣bx+2中,当x=﹣1时,y=4;当x=﹣2时 y=0.
(1)根据已知条件可知这个函数的表达式 .
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点 成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.
22.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1 ,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
23.如图分别是五角星、六角星、七角星、八角星的图形;
(1)请问其中是中心对称图形的是哪些?
(2)依次类推,36角星是不是中心对称图形?
(3)怎样判断一个n角星是否是中心对称图形?
【参考答案】
1.B
2.B
3.A
4.A
5.D
6.C
7.A
8.C
9.C
10.C
11.2
12.
13.(0,1).
14.(2,1)
15.② ⑤或⑥或⑦
16.(1)直线AD、BE、CF以及线段AB、BC、CD的垂直平分线都是这个正六边形的对称轴.
(2)因为正六边的中心角为60°,正六边形绕点O旋转60°或其整数倍后能和原来的图形重合.
(3)一般地,正n边形每条边的垂直平分线都是对称轴;
当n是偶数时,相对顶点的连线也是对称轴;
绕正n边形的中心旋转或其整数倍都能与原来的图形重合.
17.解: 腰长为cm,底边长为2cm的等腰三角形,
由三线合一得:底边的一半为
由勾股定理得:底边上的高为:
如图,拼成平行四边形,
此时平行四边形的周长为:
如图,拼成平行四边形如下:
此时平行四边形的周长为:
如图,拼成矩形如下图,
此时矩形的周长为:
18.解:(1)如图,△A1B1C1即为所求,A1的坐标为(﹣2,﹣2).
故答案为:(﹣2,﹣2).
(2)如图,△A2B2C2即为所求,A2的坐标为(4,6).
故答案为:(4,6).
(3)旋转中心P的坐标为(1,2),
故答案为:(1,2).
19.(1)先根据旋转的性质画出点,再顺次连接点即可得,如图所示:
设点的坐标为,
点C是的中点,且,,
,解得,
,
同理可得:;
(2),
从点A到点的平移方式为向下平移8个单位长度,
,
,即,
先画出点,再顺次连接点即可得,如图所示:
(3)由旋转中心的定义得:线段的中点P即为旋转中心,
,
,即,
故旋转中心的坐标为.
20.解:(1)如图所示:
为所求作的图形
(2)如图所示:
为所求作的图形
(3)将与的对应顶点连线,可得对应中心坐标为 (0,0),
的面积等于三个顶点所在的正方形的面积减去三个小三角形的面积:
S△ABC=
21.解:(1)由题意:,解得:,
∴函数解析式为:y=x3﹣3x+2.
故答案为:y=x3﹣3x+2.
(2)函数图象如图所示:
(3)①观察图象可知:函数图象关于(0,2)成中心对称.
故答案为:(0,﹣2).
②观察图象可知:当﹣1<x<1时,y随着x的增大而减小.
③观察图象可知:若直线y=c与该图象有3个交点,c的取值范围为0<c<4.
22.(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
考点:1、中心对称;2、坐标与图形性质
23.解:(1)图中是中心对称图形的有六角星,八角星;
(2)由(1)知六角星,八角星,十角星,都是中心对称图形,由此可知,当角的个数为偶数个时,它是中心对称图形,因此36角星也是中心对称图形;
(3)当n是偶数时,n角星绕中心点旋转180°能完全重合,n角星是中心对称图形;
当n奇数时,n角星绕中心点旋转180°不能完全重合,n角星不是中心对称图形.
一、选择题
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.下面的图形是用数学家名字命名的,其中是轴对称图形,但不是中心对称图形的是( )
A.科克曲线 B.笛卡尔心形线
C.赵爽弦图 D.斐波那契螺旋线
3.下列命题:①顺次连接菱形各边中点得到的四边形是矩形;②平行四边形既是中心对称图形又是轴对称图形;③的算术平方根是3;④对于任意实数m,关于x的方程有两个不相等的实数根.其中正确的命题个数是( )
A.1个 B.2个 C.3个 D.4个
4.下列图形中,是中心对称图形但不是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
5.如图所示的两个三角形(B、F、C、E四点共线)是中心对称图形,则对称中心是( )
A.点C B.点D
C.线段BC的中点 D.线段FC的中点
6.下列说法中,正确的是( )
A.形状和大小完全相同的两个图形成中心对称
B.成中心对称的两个图形必重合
C.成中心对称的两个图形形状和大小完全相同
D.旋转后能重合的两个图形成中心对称
7.如图,和关于点成中心对称,则点坐标是( )
A. B. C. D.
8.如图是的网格图,将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
A.① B.② C.③ D.④
9.如图,在4×4的网格纸中,ABC的三个顶点都在格点上,现要在这张网格纸的四个格点M,N,P,Q中找一点作为旋转中心.将ABC绕着这个中心进行旋转,旋转前后的两个三角形成中心对称,且旋转后的三角形的三个顶点都在这张4×4的网格纸的格点上,那么满足条件的旋转中心有( )
A.点M,点N B.点M,点Q C.点N,点P D.点P,点Q
10.若两个图形成中心对称,则下列说法:
①对应点的连线必经过对称中心;②这两个图形的形状和大小完全相同;
③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转某个角度后必与另一个图形重合.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.给出下列5种图形:①平行四边形②菱形③正五边形、④正六边形、⑤等腰梯形中,既是轴对称又是中心对称的图形有________个.
12.如下图所示的四个图形中,是中心对称图形的是__________,是轴对称图形的__________. (填序号)
13.在棋盘中建立如图所示的平面直角坐标系,三颗棋子 A,O,B 的位置如图所示,它们的坐标分别是(﹣1,1),(0,0)和(1,0),在其他点位置添加一颗棋子 P,使 A,O,B,P 四颗棋子成为一个中心对称图形,请写出棋子 P 的位置坐标_____(写出 1 个即可).
14.如图,在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为_____.
15.在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影构成中心对称图形,涂黑的小正方形序号为__________;若与图中阴影构成轴对称图形,涂黑的小正方形序号为__________.
三、解答题
16.如图,点O是正六边形ABCDEF的中心.
(1)找出这个轴对称图形的对称轴;
(2)这个正六边形绕点O旋转多少度后能和原来的图形重合?
(3)如果换成其他的正多边形呢?能得到一般的结论吗?
17.有一腰长为cm,底边长为2cm的等腰三角形纸片,如下图,小明沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片.请用这两个直角三角形纸片拼一个成中心对称的四边形,画出所有可能的示意图(标注好各边长),并在图形下方直接写出该四边形的周长.
18.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(2,﹣2),B(0,﹣5),C(0,﹣2).
(1)画△A1B1C1,使它与△ABC关于点C成中心对称,则A1的坐标为 .
(2)平移△ABC,使点B的对应点B2的坐标为(2,3),画出平移后对应的△A2B2C2,则A2的坐标为 .
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,则旋转中心的坐标为 .
19.如图,方格纸中每个小正方形的边长均为1个单位长度,小正方形的顶点成为格点.的三个顶点、、.
(1)将以点C为旋转中心旋转180°,得到,画出,并直接写出点、的坐标;
(2)平移,使点A的对应点为,请画出平移后对应的;
(3)若将绕某一点旋转可得到,请直接写出旋转中心的坐标.
20.如图,在网格图中建立平面直角坐标系,的顶点坐标为、、.
(1)若将向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的;
(2)画出绕C1顺时针方向旋转90°后得到的;
(3)与是中心对称图形,请写出对称中心的坐标: ;并计算的面积: .
21.在学习函数的过程中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=ax3﹣bx+2中,当x=﹣1时,y=4;当x=﹣2时 y=0.
(1)根据已知条件可知这个函数的表达式 .
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点 成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.
22.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1 ,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
23.如图分别是五角星、六角星、七角星、八角星的图形;
(1)请问其中是中心对称图形的是哪些?
(2)依次类推,36角星是不是中心对称图形?
(3)怎样判断一个n角星是否是中心对称图形?
【参考答案】
1.B
2.B
3.A
4.A
5.D
6.C
7.A
8.C
9.C
10.C
11.2
12.
13.(0,1).
14.(2,1)
15.② ⑤或⑥或⑦
16.(1)直线AD、BE、CF以及线段AB、BC、CD的垂直平分线都是这个正六边形的对称轴.
(2)因为正六边的中心角为60°,正六边形绕点O旋转60°或其整数倍后能和原来的图形重合.
(3)一般地,正n边形每条边的垂直平分线都是对称轴;
当n是偶数时,相对顶点的连线也是对称轴;
绕正n边形的中心旋转或其整数倍都能与原来的图形重合.
17.解: 腰长为cm,底边长为2cm的等腰三角形,
由三线合一得:底边的一半为
由勾股定理得:底边上的高为:
如图,拼成平行四边形,
此时平行四边形的周长为:
如图,拼成平行四边形如下:
此时平行四边形的周长为:
如图,拼成矩形如下图,
此时矩形的周长为:
18.解:(1)如图,△A1B1C1即为所求,A1的坐标为(﹣2,﹣2).
故答案为:(﹣2,﹣2).
(2)如图,△A2B2C2即为所求,A2的坐标为(4,6).
故答案为:(4,6).
(3)旋转中心P的坐标为(1,2),
故答案为:(1,2).
19.(1)先根据旋转的性质画出点,再顺次连接点即可得,如图所示:
设点的坐标为,
点C是的中点,且,,
,解得,
,
同理可得:;
(2),
从点A到点的平移方式为向下平移8个单位长度,
,
,即,
先画出点,再顺次连接点即可得,如图所示:
(3)由旋转中心的定义得:线段的中点P即为旋转中心,
,
,即,
故旋转中心的坐标为.
20.解:(1)如图所示:
为所求作的图形
(2)如图所示:
为所求作的图形
(3)将与的对应顶点连线,可得对应中心坐标为 (0,0),
的面积等于三个顶点所在的正方形的面积减去三个小三角形的面积:
S△ABC=
21.解:(1)由题意:,解得:,
∴函数解析式为:y=x3﹣3x+2.
故答案为:y=x3﹣3x+2.
(2)函数图象如图所示:
(3)①观察图象可知:函数图象关于(0,2)成中心对称.
故答案为:(0,﹣2).
②观察图象可知:当﹣1<x<1时,y随着x的增大而减小.
③观察图象可知:若直线y=c与该图象有3个交点,c的取值范围为0<c<4.
22.(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
考点:1、中心对称;2、坐标与图形性质
23.解:(1)图中是中心对称图形的有六角星,八角星;
(2)由(1)知六角星,八角星,十角星,都是中心对称图形,由此可知,当角的个数为偶数个时,它是中心对称图形,因此36角星也是中心对称图形;
(3)当n是偶数时,n角星绕中心点旋转180°能完全重合,n角星是中心对称图形;
当n奇数时,n角星绕中心点旋转180°不能完全重合,n角星不是中心对称图形.
同课章节目录
