人教版九年级下册数学26.1.2反比例函数的图像和性质-反比例函数与一次函数综合训练(word版、含答案)
文档属性
| 名称 | 人教版九年级下册数学26.1.2反比例函数的图像和性质-反比例函数与一次函数综合训练(word版、含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 377.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 17:43:58 | ||
图片预览

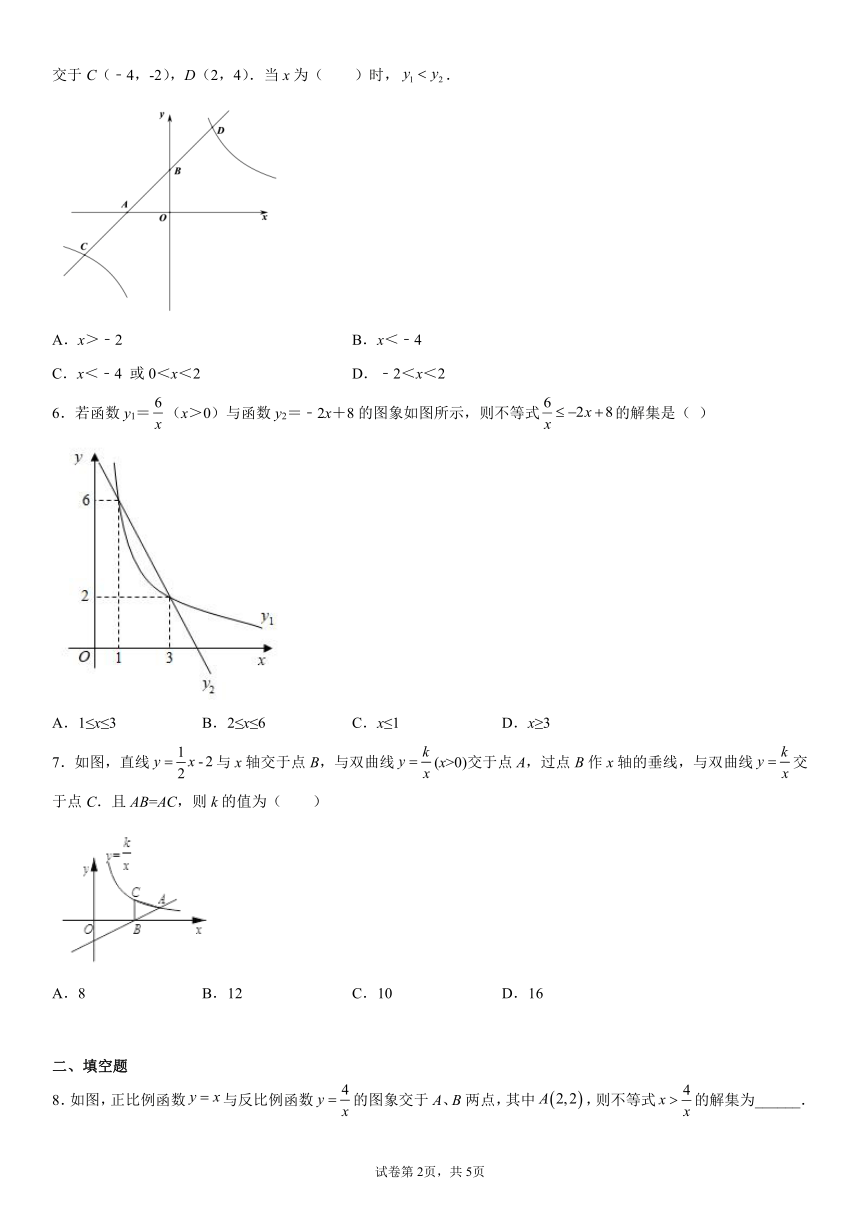
文档简介
人教版九年级下册数学26.1.2反比例函数的图像和性质-反比例函数与一次函数综合训练
一、单选题
1.函数与的图象的两个交点的坐标分别为,,则,的值分别是( )
A.2,﹣3 B.﹣2,﹣3 C.﹣2,3 D.2,3
2.在同一坐标系中,函数和的图象大致是( )
A. B. C. D.
3.正比例函数y=x与反比例函数y=的图象相交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D(如图),则四边形ABCD的面积为( )
A.1 B. C.2 D.
4.如图,反比例函数的图象与一次函数的图象交于M、N两点,已知点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于的方程的解为( )
A.或1 B.或3
C.或1 D.或1
5.如图,一次函数y1=k1+b(k1≠0)的图象分别与x轴、y轴相交于点A、B,与反比例函数的图象交于C(﹣4,-2),D(2,4).当x为( )时,.
A.x>﹣2 B.x<﹣4
C.x<﹣4 或0<x<2 D.﹣2<x<2
6.若函数y1=(x>0)与函数y2=﹣2x+8的图象如图所示,则不等式的解集是( )
A.1≤x≤3 B.2≤x≤6 C.x≤1 D.x≥3
7.如图,直线与x轴交于点B,与双曲线(x>0)交于点A,过点B作x轴的垂线,与双曲线交于点C.且AB=AC,则k的值为( )
A.8 B.12 C.10 D.16
二、填空题
8.如图,正比例函数与反比例函数的图象交于A、B两点,其中,则不等式的解集为______.
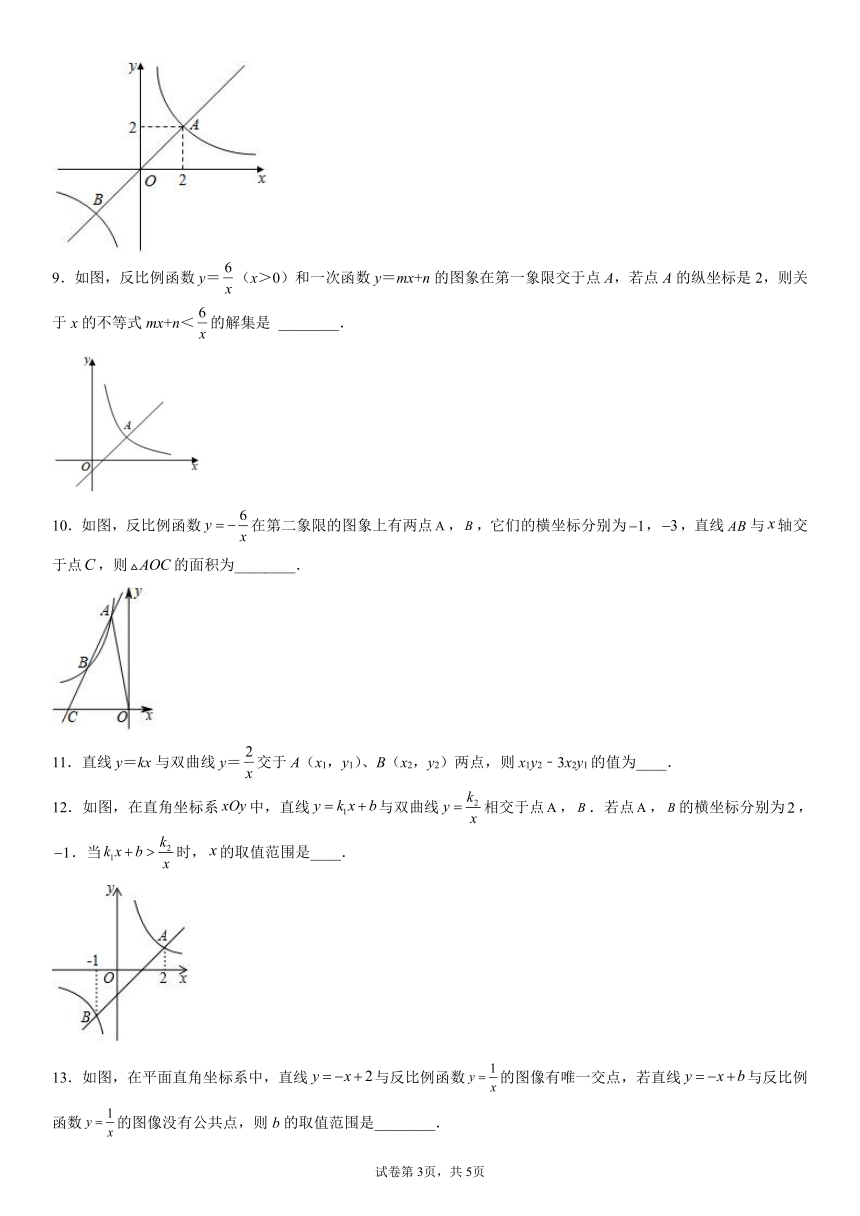
9.如图,反比例函数y=(x>0)和一次函数y=mx+n的图象在第一象限交于点A,若点A的纵坐标是2,则关于x的不等式mx+n<的解集是 ________.
10.如图,反比例函数在第二象限的图象上有两点,,它们的横坐标分别为,,直线与轴交于点,则的面积为________.
11.直线y=kx与双曲线y=交于A(x1,y1)、B(x2,y2)两点,则x1y2﹣3x2y1的值为____.
12.如图,在直角坐标系中,直线与双曲线相交于点,.若点,的横坐标分别为,.当时,的取值范围是____.
13.如图,在平面直角坐标系中,直线与反比例函数的图像有唯一交点,若直线与反比例函数的图像没有公共点,则b的取值范围是________.
14.如图,一次函数的图象与x轴交于A点,与y轴交于B点,与反比例函数的图象交于点和点F.则不等式的解集是___________.
三、解答题
15.如图,一次函数y=kx+b与反比例函数的图象交于A(1,6)、B(3,n)两点,与x轴交于点C.
(1)求一次函数的表达式;
(2)若点M在x轴上,且ΔAMC的面积为6,求点M的坐标.
16.如图,直线y=kx与反比例函数(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值;
(2)求OBC的面积;
17.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(-1,n)、B(2,-1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)请直接写出不等式kx+b>的解集;
(3)若点D与点C关于x轴对称,求△ABD的面积.
18.如图,一次函数y=ax+b的图象与y轴交于点B(0,2),与x轴交于点E(﹣,0)与反比例函数(x<0)的图象交于点D.以BD为对角线作矩形ABCD,使顶点A、C落在x轴上(点A在点C的右边).
(1)求一次函数的解析式.
(2)求点C和点D的坐标以及反比例函数的解析式.
(3)直接写出在第三象限内,x取何值时<ax+b.
参考答案
1.A
2.A
3.C
4.A
5.C
6.A
7.D
8.﹣
9.0<x<3
10.12
11.4
12.-1<x<0或x>2
13.
14.<或
15.(1)y=﹣2x+8;(2)点M的坐标为(6,0)或(2,0).
16.(1)2;(2)1
17.(1);y=-x+1;(2)0<x<2或x<-1;(3)3.
18.(1);(2),,;(3)
试卷第4页,共5页
试卷第5页,共5页
一、单选题
1.函数与的图象的两个交点的坐标分别为,,则,的值分别是( )
A.2,﹣3 B.﹣2,﹣3 C.﹣2,3 D.2,3
2.在同一坐标系中,函数和的图象大致是( )
A. B. C. D.
3.正比例函数y=x与反比例函数y=的图象相交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D(如图),则四边形ABCD的面积为( )
A.1 B. C.2 D.
4.如图,反比例函数的图象与一次函数的图象交于M、N两点,已知点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于的方程的解为( )
A.或1 B.或3
C.或1 D.或1
5.如图,一次函数y1=k1+b(k1≠0)的图象分别与x轴、y轴相交于点A、B,与反比例函数的图象交于C(﹣4,-2),D(2,4).当x为( )时,.
A.x>﹣2 B.x<﹣4
C.x<﹣4 或0<x<2 D.﹣2<x<2
6.若函数y1=(x>0)与函数y2=﹣2x+8的图象如图所示,则不等式的解集是( )
A.1≤x≤3 B.2≤x≤6 C.x≤1 D.x≥3
7.如图,直线与x轴交于点B,与双曲线(x>0)交于点A,过点B作x轴的垂线,与双曲线交于点C.且AB=AC,则k的值为( )
A.8 B.12 C.10 D.16
二、填空题
8.如图,正比例函数与反比例函数的图象交于A、B两点,其中,则不等式的解集为______.
9.如图,反比例函数y=(x>0)和一次函数y=mx+n的图象在第一象限交于点A,若点A的纵坐标是2,则关于x的不等式mx+n<的解集是 ________.
10.如图,反比例函数在第二象限的图象上有两点,,它们的横坐标分别为,,直线与轴交于点,则的面积为________.
11.直线y=kx与双曲线y=交于A(x1,y1)、B(x2,y2)两点,则x1y2﹣3x2y1的值为____.
12.如图,在直角坐标系中,直线与双曲线相交于点,.若点,的横坐标分别为,.当时,的取值范围是____.
13.如图,在平面直角坐标系中,直线与反比例函数的图像有唯一交点,若直线与反比例函数的图像没有公共点,则b的取值范围是________.
14.如图,一次函数的图象与x轴交于A点,与y轴交于B点,与反比例函数的图象交于点和点F.则不等式的解集是___________.
三、解答题
15.如图,一次函数y=kx+b与反比例函数的图象交于A(1,6)、B(3,n)两点,与x轴交于点C.
(1)求一次函数的表达式;
(2)若点M在x轴上,且ΔAMC的面积为6,求点M的坐标.
16.如图,直线y=kx与反比例函数(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值;
(2)求OBC的面积;
17.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(-1,n)、B(2,-1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)请直接写出不等式kx+b>的解集;
(3)若点D与点C关于x轴对称,求△ABD的面积.
18.如图,一次函数y=ax+b的图象与y轴交于点B(0,2),与x轴交于点E(﹣,0)与反比例函数(x<0)的图象交于点D.以BD为对角线作矩形ABCD,使顶点A、C落在x轴上(点A在点C的右边).
(1)求一次函数的解析式.
(2)求点C和点D的坐标以及反比例函数的解析式.
(3)直接写出在第三象限内,x取何值时<ax+b.
参考答案
1.A
2.A
3.C
4.A
5.C
6.A
7.D
8.﹣
9.0<x<3
10.12
11.4
12.-1<x<0或x>2
13.
14.<或
15.(1)y=﹣2x+8;(2)点M的坐标为(6,0)或(2,0).
16.(1)2;(2)1
17.(1);y=-x+1;(2)0<x<2或x<-1;(3)3.
18.(1);(2),,;(3)
试卷第4页,共5页
试卷第5页,共5页
