人教版数学九上25.1.2概率课件(共20张PPT)
文档属性
| 名称 | 人教版数学九上25.1.2概率课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 976.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 20:08:53 | ||
图片预览






文档简介
(共20张PPT)
25.1.2 概 率
A
B
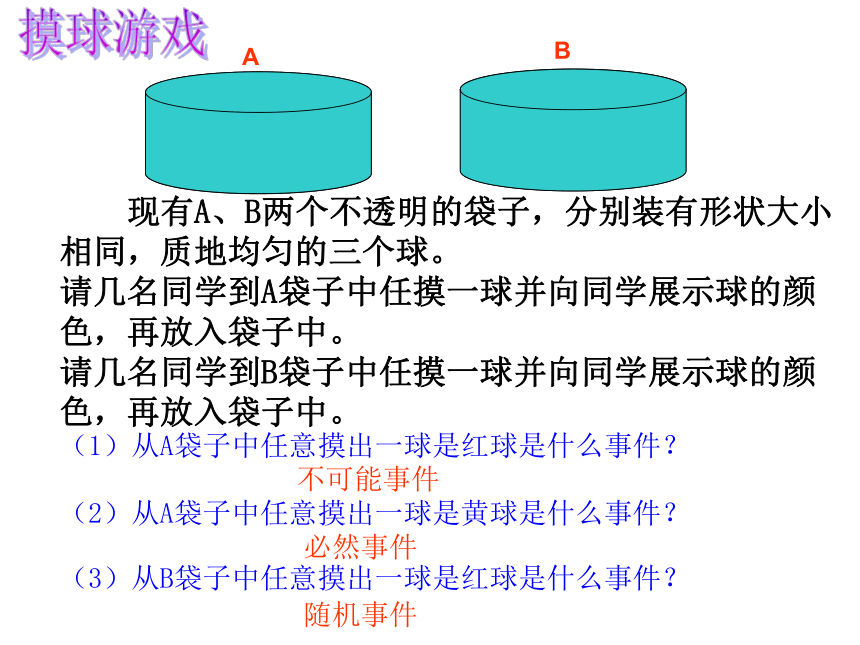
现有A、B两个不透明的袋子,分别装有形状大小相同,质地均匀的三个球。
请几名同学到A袋子中任摸一球并向同学展示球的颜色,再放入袋子中。
请几名同学到B袋子中任摸一球并向同学展示球的颜色,再放入袋子中。
(1)从A袋子中任意摸出一球是红球是什么事件?
不可能事件
(2)从A袋子中任意摸出一球是黄球是什么事件?
必然事件
(3)从B袋子中任意摸出一球是红球是什么事件?
随机事件
6种
出现每种结果的可能性相等,
“向上一面的点数为6”的可能性大小是
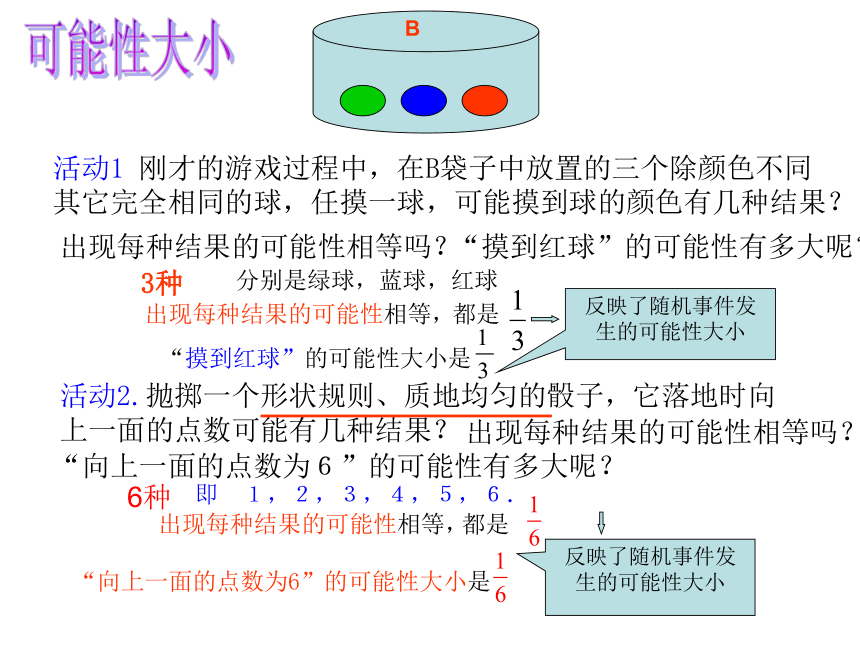
活动2.抛掷一个形状规则、质地均匀的骰子,它落地时向上一面的点数可能有几种结果?
出现每种结果的可能性相等吗?
“向上一面的点数为6”的可能性有多大呢?
即 1,2,3,4,5,6.
都是
活动1 刚才的游戏过程中,在B袋子中放置的三个除颜色不同其它完全相同的球,任摸一球,可能摸到球的颜色有几种结果?
B
出现每种结果的可能性相等吗?
3种
分别是绿球,蓝球,红球
“摸到红球”的可能性有多大呢?
出现每种结果的可能性相等,
都是
“摸到红球”的可能性大小是
反映了随机事件发生的可能性大小
反映了随机事件发生的可能性大小
记为:P( A)
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件发生的概率(probability ),
“向上一面的点数为6”的概率:
P(向上一面的点数为6)=
记为:
记为:
P(抽到红球)=
“抽到红球”的概率:
eg:
判断对错
×
②明天下雨的概率是80%,则明天不下雨的可能性是20%。( )
√
①“十一”黄金周期间,某商场举办购物抽奖活动,其门前公告中说:“抽奖中奖的概率为 ”,小强看了公告后高兴地告诉妈妈:“我抽10次一定会有一次中奖的 ( )
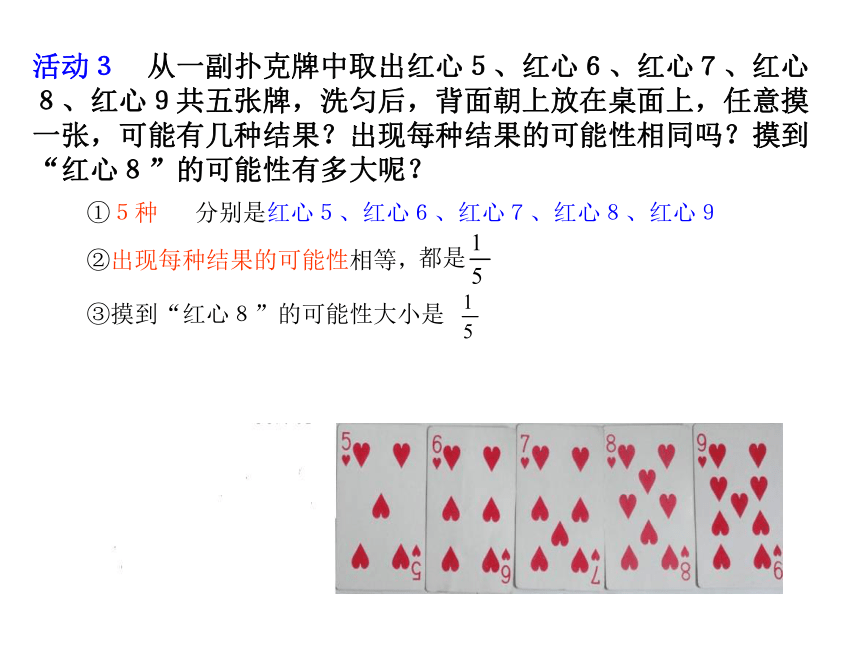
活动3 从一副扑克牌中取出红心5、红心6、红心7、红心 8、红心9共五张牌,洗匀后,背面朝上放在桌面上,任意摸一张,可能有几种结果?出现每种结果的可能性相同吗?摸到“红心8”的可能性有多大呢?
①5种
分别是红心5、红心6、红心7、红心8、红心9
②出现每种结果的可能性相等,
都是
③摸到“红心8”的可能性大小是
活动3. 从一副扑克牌取出红心5、红心6、红心7、红心8、红心9,各张牌形状、大小、质地相同,洗匀后,任意摸一张,摸到的牌有几种结果?出现每钟结果的可能性相同吗?
5种
出现每种结果的可能性相等
出现每种结果的可能性相等
活动2.抛掷一个形状规则、质地均匀的骰(tóu)子,任抛一次它落地时向上的数可能有几种结果?
出现每种结果的可能性相同吗?
即1,2,3,4,5,6.
6种
活动1 刚才的游戏过程中,在B盒中放置的三个除颜色不同其它完全相同的球,任摸一球,可能摸到球的颜色有几种结果?
出现每种结果的可能性相同吗?
3种
即绿球 , 蓝球 , 红球 .
出现每种结果的可能性相等
即红心5、红心6、红心7、红心8、红心9
以上试验有两个特征:
等可能事件
1.每一次试验中,可能出现的结果只有有限个;
2.每一次试验中,各种结果出现的可能性相等;
(有限)
1.自由转动如图三色转盘一次,事件“指针落在红色区域”的概率为 .
下列说法对吗 请说明理由.
2.足球赛篮球比赛中,裁判员通过掷硬币决定哪个队先发球,这样的游戏公平.
P(随机事件) 所有可能出现的结果数 事件 发生可能出现的结果数 如何计算
3
1
6
1
5
1
5
2
n
m
P(A)=
找一找(对一个等可能性事件有什么方法能求出其概率)
A
1
6
1
5
P(摸到红球)=
P(向上一面点数为6)=
P(摸到红心8)=
P(摸到红心6或8)=
1
5
1
6
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为
P(A)=
例1 掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数 有3种可能,
(3)点数大于2且小于5 有2种可能,即点数为 3,4,
P(点数为奇数)=
P(点数大于2且小于5)=
解:
掷一个骰子时,向上一面的点数可能为
1,2,3,4,5,6.共6种
这些点数出现的可能性相等.
(1)P(点数为2)=
即点数为 1,3,5,
(2)点数为奇数;
(3)点数大于2且小于5.
2、再找事件出现的结果数.
求一个事件的概率,关键抓住两点
1、先找出一次试验中所有可能出现的结果数及是否是等可能的.
概率P(A)的取值范围:
0 ≤ P(A) ≤ 1
当A为必然事件时,P(A) = 1.
当A为不可能事件时,P(A) = 0.
0
1
不可能事件
必然事件
事件发生的可能性越来越小
事件发生的可能性越来越大
概率的值
思考:掷一个骰子观察向上一面点数为0的概率
是多少?点数小于7的概率是多少?
D
B
小明家
1.从一副没有“大小王”的扑克牌中随机地抽取一张, “抽到红心5”的概率是( )
A . B . C . D .
2.小明暑假去同学家,走到一个十字路口处,忘记了前面哪条路通往同学家,如图所示,那么他能一次选对路的概率是( )
十字路口
同学家
A. B. C. D.
A. 3个 B. 9个 C. 4个 D. 6个
3.在一个不透明的口袋中装有若干个只有颜色不同的球,如果口袋中装有1个蓝球,且摸出蓝球概率为 ,那么袋中球的个数为( )
A
4.如图,从一副牌中取出红心2至红心9共8张牌,随意抽出一张.
(1)摸到”红心3”的概率;
(3)摸到“4的倍数”的概率;
(4)请你设计一个事件使它的概率等于 .
解:随意抽一张时,可能为红心2,3,4,5,6,7,8,9,共8种,这些结果出现的可能性相等.
(1)P(红心3)=
(3)
4的倍数有2种可能,即红心4,8.
P(4的倍数)=
(2)摸到“偶数”的概率
P(偶数)=
(2)
摸到偶数有4种可能,即红心2,4,6,8.
5、某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券(转盘被等分20个扇形).
(1)他得到100元购物券的概率是多少?
(2)他得到50元购物券的概率是多少?
(3)他得到20元购物券的概率是多少?
一种思想:类比
一个定义:对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件发生的概率,记为P(A).
一个公式:
两个特征:有限性、等可能性.
P(A)=
事件A发生的结果数
所有可能出现的总结果数
1.教科书第134页第3、4、5题;
2.上网收集与概率有关的故事、名言、生 活实例.
(1) 甲自由转动转盘A,同时乙自由转动转盘B;
(2) 转盘停止后,指针指向几就顺时针走几格,得到一个
数字 (如,在转盘A中, 如果指针指向3, 就按顺时针方向
走3格,得到数字6);
(3) 如果最终得到的数字是偶数就得1分,否则不得分;
(4) 转动10次转盘,记录每次得分的结果,累计得分高的
人为胜者。
7.本图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形。利用这两个转盘做下面的游戏:
这个游戏对甲、乙双方公平吗?
说说你的理由。
1
2
3
4
5
6
1
3
5
2
4
6
A
B
25.1.2 概 率
A
B
现有A、B两个不透明的袋子,分别装有形状大小相同,质地均匀的三个球。
请几名同学到A袋子中任摸一球并向同学展示球的颜色,再放入袋子中。
请几名同学到B袋子中任摸一球并向同学展示球的颜色,再放入袋子中。
(1)从A袋子中任意摸出一球是红球是什么事件?
不可能事件
(2)从A袋子中任意摸出一球是黄球是什么事件?
必然事件
(3)从B袋子中任意摸出一球是红球是什么事件?
随机事件
6种
出现每种结果的可能性相等,
“向上一面的点数为6”的可能性大小是
活动2.抛掷一个形状规则、质地均匀的骰子,它落地时向上一面的点数可能有几种结果?
出现每种结果的可能性相等吗?
“向上一面的点数为6”的可能性有多大呢?
即 1,2,3,4,5,6.
都是
活动1 刚才的游戏过程中,在B袋子中放置的三个除颜色不同其它完全相同的球,任摸一球,可能摸到球的颜色有几种结果?
B
出现每种结果的可能性相等吗?
3种
分别是绿球,蓝球,红球
“摸到红球”的可能性有多大呢?
出现每种结果的可能性相等,
都是
“摸到红球”的可能性大小是
反映了随机事件发生的可能性大小
反映了随机事件发生的可能性大小
记为:P( A)
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件发生的概率(probability ),
“向上一面的点数为6”的概率:
P(向上一面的点数为6)=
记为:
记为:
P(抽到红球)=
“抽到红球”的概率:
eg:
判断对错
×
②明天下雨的概率是80%,则明天不下雨的可能性是20%。( )
√
①“十一”黄金周期间,某商场举办购物抽奖活动,其门前公告中说:“抽奖中奖的概率为 ”,小强看了公告后高兴地告诉妈妈:“我抽10次一定会有一次中奖的 ( )
活动3 从一副扑克牌中取出红心5、红心6、红心7、红心 8、红心9共五张牌,洗匀后,背面朝上放在桌面上,任意摸一张,可能有几种结果?出现每种结果的可能性相同吗?摸到“红心8”的可能性有多大呢?
①5种
分别是红心5、红心6、红心7、红心8、红心9
②出现每种结果的可能性相等,
都是
③摸到“红心8”的可能性大小是
活动3. 从一副扑克牌取出红心5、红心6、红心7、红心8、红心9,各张牌形状、大小、质地相同,洗匀后,任意摸一张,摸到的牌有几种结果?出现每钟结果的可能性相同吗?
5种
出现每种结果的可能性相等
出现每种结果的可能性相等
活动2.抛掷一个形状规则、质地均匀的骰(tóu)子,任抛一次它落地时向上的数可能有几种结果?
出现每种结果的可能性相同吗?
即1,2,3,4,5,6.
6种
活动1 刚才的游戏过程中,在B盒中放置的三个除颜色不同其它完全相同的球,任摸一球,可能摸到球的颜色有几种结果?
出现每种结果的可能性相同吗?
3种
即绿球 , 蓝球 , 红球 .
出现每种结果的可能性相等
即红心5、红心6、红心7、红心8、红心9
以上试验有两个特征:
等可能事件
1.每一次试验中,可能出现的结果只有有限个;
2.每一次试验中,各种结果出现的可能性相等;
(有限)
1.自由转动如图三色转盘一次,事件“指针落在红色区域”的概率为 .
下列说法对吗 请说明理由.
2.足球赛篮球比赛中,裁判员通过掷硬币决定哪个队先发球,这样的游戏公平.
P(随机事件) 所有可能出现的结果数 事件 发生可能出现的结果数 如何计算
3
1
6
1
5
1
5
2
n
m
P(A)=
找一找(对一个等可能性事件有什么方法能求出其概率)
A
1
6
1
5
P(摸到红球)=
P(向上一面点数为6)=
P(摸到红心8)=
P(摸到红心6或8)=
1
5
1
6
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为
P(A)=
例1 掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数 有3种可能,
(3)点数大于2且小于5 有2种可能,即点数为 3,4,
P(点数为奇数)=
P(点数大于2且小于5)=
解:
掷一个骰子时,向上一面的点数可能为
1,2,3,4,5,6.共6种
这些点数出现的可能性相等.
(1)P(点数为2)=
即点数为 1,3,5,
(2)点数为奇数;
(3)点数大于2且小于5.
2、再找事件出现的结果数.
求一个事件的概率,关键抓住两点
1、先找出一次试验中所有可能出现的结果数及是否是等可能的.
概率P(A)的取值范围:
0 ≤ P(A) ≤ 1
当A为必然事件时,P(A) = 1.
当A为不可能事件时,P(A) = 0.
0
1
不可能事件
必然事件
事件发生的可能性越来越小
事件发生的可能性越来越大
概率的值
思考:掷一个骰子观察向上一面点数为0的概率
是多少?点数小于7的概率是多少?
D
B
小明家
1.从一副没有“大小王”的扑克牌中随机地抽取一张, “抽到红心5”的概率是( )
A . B . C . D .
2.小明暑假去同学家,走到一个十字路口处,忘记了前面哪条路通往同学家,如图所示,那么他能一次选对路的概率是( )
十字路口
同学家
A. B. C. D.
A. 3个 B. 9个 C. 4个 D. 6个
3.在一个不透明的口袋中装有若干个只有颜色不同的球,如果口袋中装有1个蓝球,且摸出蓝球概率为 ,那么袋中球的个数为( )
A
4.如图,从一副牌中取出红心2至红心9共8张牌,随意抽出一张.
(1)摸到”红心3”的概率;
(3)摸到“4的倍数”的概率;
(4)请你设计一个事件使它的概率等于 .
解:随意抽一张时,可能为红心2,3,4,5,6,7,8,9,共8种,这些结果出现的可能性相等.
(1)P(红心3)=
(3)
4的倍数有2种可能,即红心4,8.
P(4的倍数)=
(2)摸到“偶数”的概率
P(偶数)=
(2)
摸到偶数有4种可能,即红心2,4,6,8.
5、某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券(转盘被等分20个扇形).
(1)他得到100元购物券的概率是多少?
(2)他得到50元购物券的概率是多少?
(3)他得到20元购物券的概率是多少?
一种思想:类比
一个定义:对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件发生的概率,记为P(A).
一个公式:
两个特征:有限性、等可能性.
P(A)=
事件A发生的结果数
所有可能出现的总结果数
1.教科书第134页第3、4、5题;
2.上网收集与概率有关的故事、名言、生 活实例.
(1) 甲自由转动转盘A,同时乙自由转动转盘B;
(2) 转盘停止后,指针指向几就顺时针走几格,得到一个
数字 (如,在转盘A中, 如果指针指向3, 就按顺时针方向
走3格,得到数字6);
(3) 如果最终得到的数字是偶数就得1分,否则不得分;
(4) 转动10次转盘,记录每次得分的结果,累计得分高的
人为胜者。
7.本图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形。利用这两个转盘做下面的游戏:
这个游戏对甲、乙双方公平吗?
说说你的理由。
1
2
3
4
5
6
1
3
5
2
4
6
A
B
同课章节目录
