人教版九年级上册数学24.2.2直线与圆的位置关系-切线长定理的应用训练(word版、含解析)
文档属性
| 名称 | 人教版九年级上册数学24.2.2直线与圆的位置关系-切线长定理的应用训练(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 20:13:36 | ||
图片预览


文档简介
人教版九年级上册数学24.2.2直线与圆的位置关系-切线长定理的应用训练
一、单选题
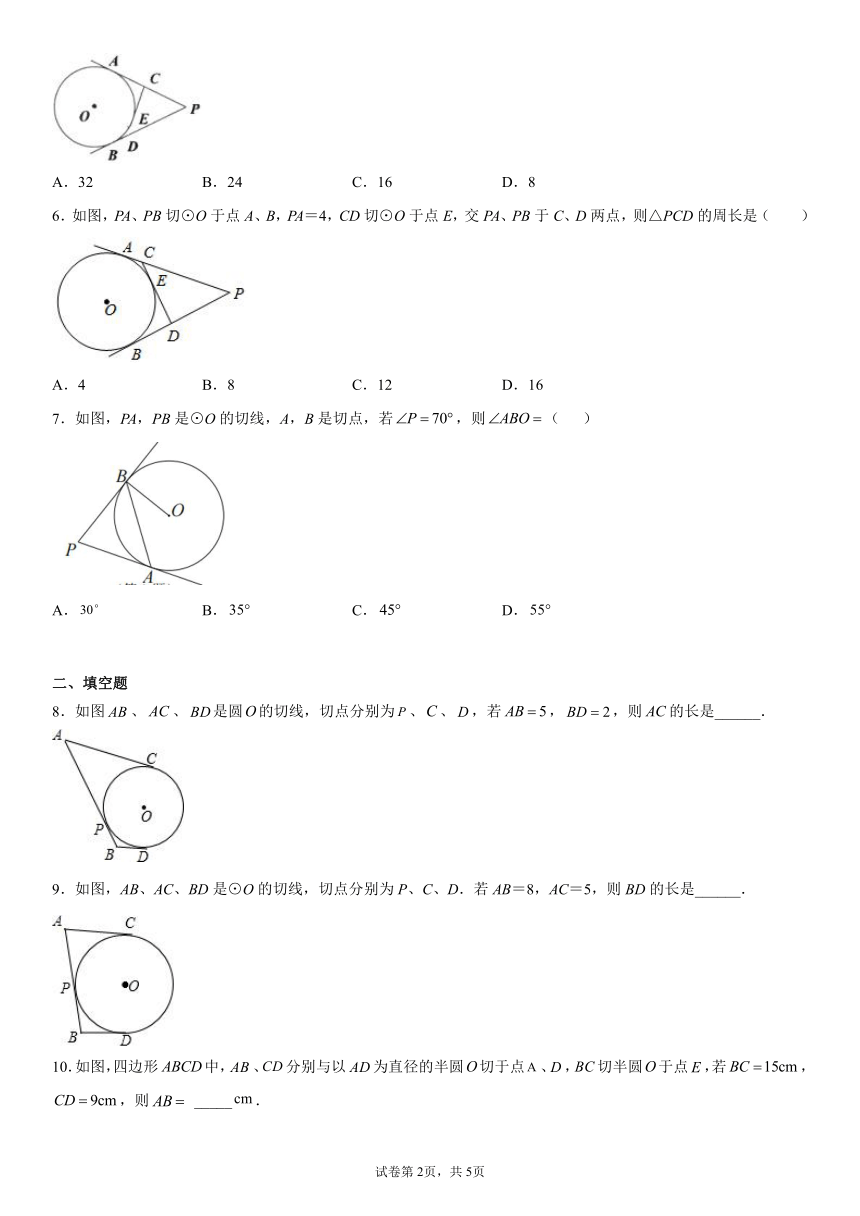
1.如图,PA、PB切⊙O于点A、B,PA=10,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( )
A.10 B.18 C.20 D.22
2.如图,是外一点,、切于点、,点在优弧上,若,则等于( )
A. B. C. D.
3.如图所示,半⊙O的直径在梯形ABCD的底边AB上,且与其余三边均相切,若BC=2,DA=3,则AB长为( )
A.4 B.5 C.6 D.不能确定
4.如图,点E为Rt△ABC的直角边AC上一点,以CE为直径的半圆与斜边AB相切于点D,连结DE.若∠B=70°,则∠CED为( )
A.70° B.65° C.55° D.35°
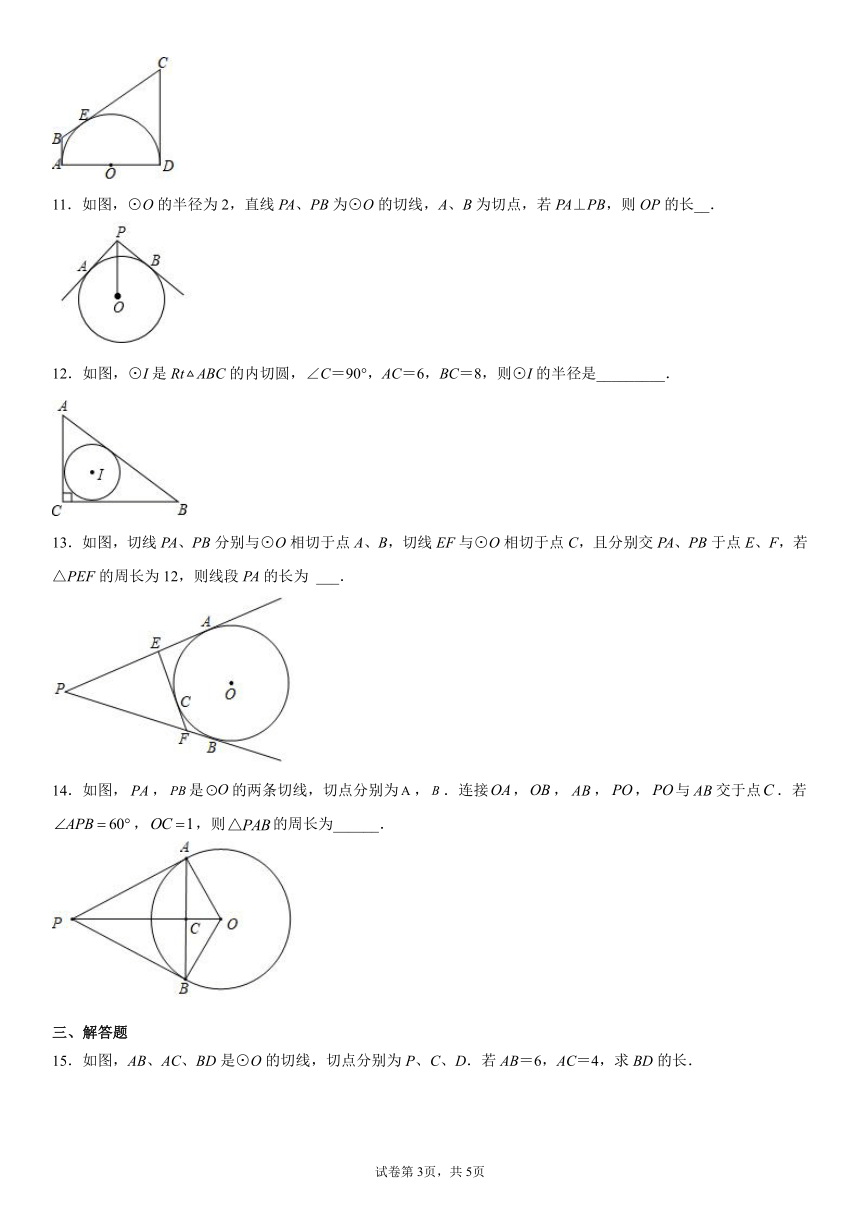
5.如图,PA、PB分别切⊙O于点A、B,且PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则PCD的周长为( )
A.32 B.24 C.16 D.8
6.如图,PA、PB切⊙O于点A、B,PA=4,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( )
A.4 B.8 C.12 D.16
7.如图,PA,PB是⊙O的切线,A,B是切点,若,则( )
A. B. C. D.
二、填空题
8.如图、、是圆的切线,切点分别为、、,若,,则的长是______.
9.如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D.若AB=8,AC=5,则BD的长是______.
10.如图,四边形中,、分别与以为直径的半圆切于点、,切半圆于点,若,,则 _____.
11.如图,⊙O的半径为2,直线PA、PB为⊙O的切线,A、B为切点,若PA⊥PB,则OP的长__.
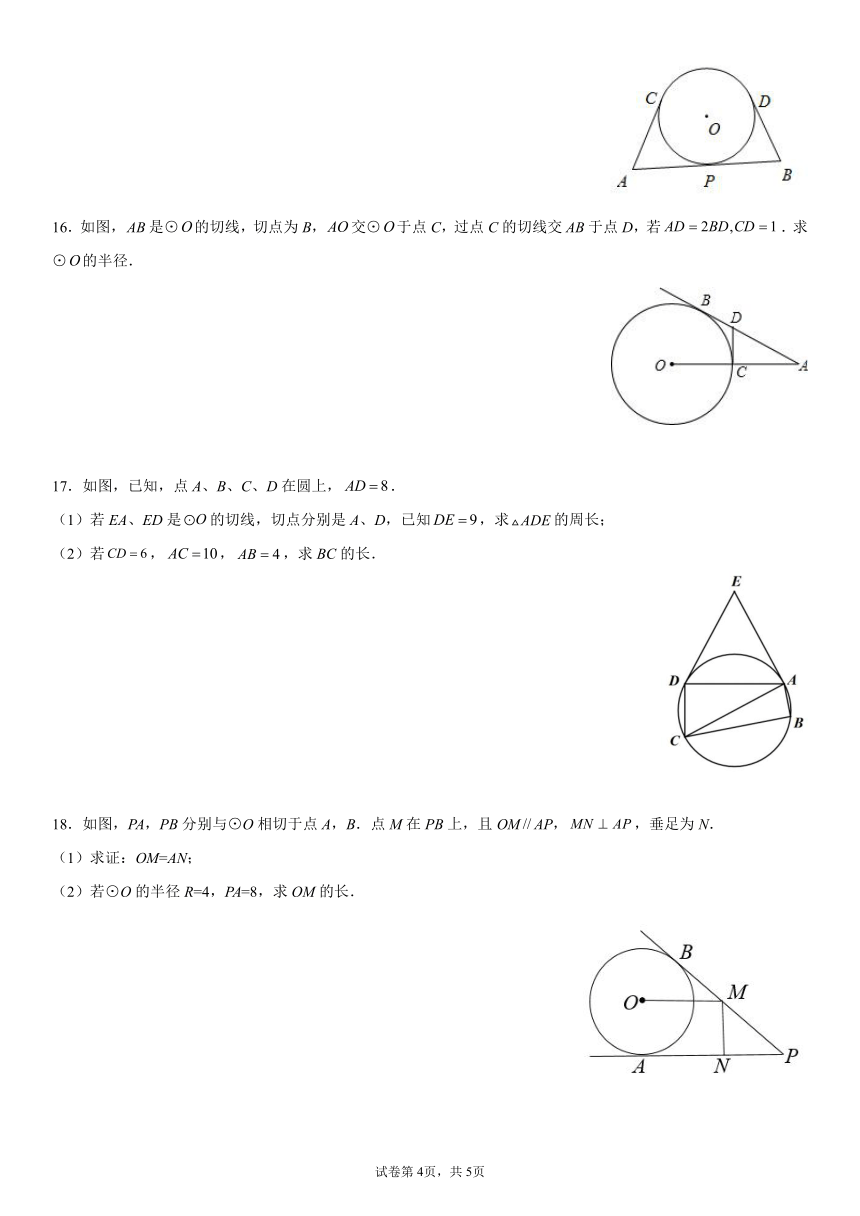
12.如图,⊙I是RtABC的内切圆,∠C=90°,AC=6,BC=8,则⊙I的半径是_________.
13.如图,切线PA、PB分别与⊙O相切于点A、B,切线EF与⊙O相切于点C,且分别交PA、PB于点E、F,若△PEF的周长为12,则线段PA的长为 ___.
14.如图,,是的两条切线,切点分别为,.连接,,,,与交于点.若,,则的周长为______.
三、解答题
15.如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D.若AB=6,AC=4,求BD的长.
16.如图,是⊙的切线,切点为B,交⊙于点C,过点C的切线交于点D,若.求⊙的半径.
17.如图,已知,点A、B、C、D在圆上,.
(1)若EA、ED是的切线,切点分别是A、D,已知,求的周长;
(2)若,,,求BC的长.
18.如图,PA,PB分别与⊙O相切于点A,B.点M在PB上,且OMAP,,垂足为N.
(1)求证:OM=AN;
(2)若⊙O的半径R=4,PA=8,求OM的长.
19.如图,PA为⊙O的切线,A为切点,过点A作AB⊥OP,垂足为点C,交⊙O于点B,延长BO与PA的延长线交于点D.
(1)求证:PB为⊙O的切线;
(2)若OB=3,OD=5,求OP的长.
20.如图所示,与△ADE各边所在直线都相切,DE⊥AE.
(1)若AE=8,AD=10,求的半径;
(2)若∠EAD=30°,求∠DOE.
参考答案
1.C
解:∵PA、PB切⊙O于点A、B,CD切⊙O于点E,
∴PA=PB=10,CA=CE,DE=DB,
∴△PCD的周长是PC+CD+PD
=PC+AC+DB+PD
=PA+PB
=10+10
=20.
故选:C.
2.C
解:、都为圆的切线,
,
,
,
与都对,
.
故选:.
3.B
解:如图,
连接OC,OD,设⊙O的半径为r,
∵BC、CD、DA与半⊙O相切,
∴在△AOD中,AD边上的高和AO边上的高都为r,
∴AO=AD,
同理BO=BC,
∴AB=AO+BO=AD+BC=2+3=5.
故选:B.
4.C
解:连接,
∵,
∴与半圆相切与点,
∵半圆与斜边AB相切于点D,
∴,
∵∠B=70°,
∴,
∴,
∵CE为直径,
∴,
∴∠CED,
故选:C.
5.C
解:∵PA、PB切⊙O于点A、B,
∴PB=PA=8,
∵CD切⊙O于点E,交PA、PB于C、D两点,
∴CA=CE,DB=DE,
∴PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=8+8=16.
则△PCD的周长是16.
故选C.
6.B
解:∵PA、PB切⊙O于点A、B,
∴PB=PA=4,
∵CD切⊙O于点E,交PA、PB于C、D两点,
∴CA=CE,DB=DE,
∴PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=4+4=8.
则△PCD的周长是8.
故选:B.
7.B
解:PA,PB是⊙O的切线,
故选:B.
8.3
解:∵AB、AC、BD是圆O的切线,
∴AC=AP,BP=BD=2,
∵AP=AB﹣BP=5﹣2=3,
∴AC=3.
故答案为3.
9.3
解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB AP=8 5=3.
故答案为:3.
10.6
解:、和都是半圆的切线,
由切线长定理得:
,,
,
,,
,
故答案为6.
11.
解:连接OA,
∵直线PA、PB为⊙O的切线,PA⊥PB,
∴OA⊥PA,∠OPA=∠APB=45°,
∴△OPA是等腰直角三角形,
∵⊙O的半径为2,
即OA=2,
∴OP=OA=2.
故答案为:.
12.2
解:如图,连接,,
在中,
,,,
,
⊙I是RtABC的内切圆,
∴,
在四边形中,
,,
四边形是正方形,
设,
由切线长定理得:,,
∵AC=6,BC=8,
∴,,
又∵,
∴,
解得:,
∴⊙I的半径是2,
故答案为:2.
13.6
解:∵切线EF与⊙O相切于点C,且分别交PA、PB于点E、F,
∴EA=EC,FC=FB,
∵△PEF的周长=PE+EF+PF=12,
∴PE+EA+FB+PF=12,
∴PA+PB=12,
又∵切线PA、PB分别与⊙O相切于点A、B,
∴PA=PB=6.
故答案为:6.
14.
解:∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,AB=2AC,PO⊥AB,
∴∠PAB=60°,
∴∠OAC=∠PAO-∠PAB=90°-60°=30°,
∴AO=2OC,
∵OC=1,
∴AO=2,
∴AC=,
∴AB=2AC=,
∴△PAB的周长=.
故答案为:.
15.2
解:∵AB、AC、BD是⊙O的切线,切点分别为P、C、D,
∴AC=AP,BP=BD,
∴BD=BP=AB AP== AB AC= 6 4=2.
16.
连接,
∵都是的切线,
∴,且,
∴,
∴,
在中,可求得,
设半径为r,则,
在中,由勾股定理可得:,
即,
解得,
∴的半径是.
17.(1)26;(2)
解:(1)∵EA、ED是的切线,,
∴,
又∵,
∴的周长;
(2),,,
∴,
∴∠ADC=90°,
∵四边形ABCD是圆的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ABC=90°,
又∵,
∴.
18.
(1)证明:连接OA,如图, ∵PA为⊙O的切线,
∴OA⊥PA, ∴∠OAP=90°,
∵ ,
∴∠AOM=90°, 而MN⊥PA,
∴∠MNA=90°,
∴四边形ANMO为矩形,
∴OM=AN;
(2)解:连接OB,如图,
∵PB为⊙O的切线, ∴OB⊥PB,OB=4,
∴∠OBM=90°,
∵四边形ANMO为矩形,
∴MN=OA=4,OM=AN,
∴OB=MN,
∵, ∴∠MPN=∠BMO,
在△PMN和△MOB中,
,
∴△PMN≌△MOB(AAS),
∴PM=OM,
∴OM=AN=PM,
∵PA、PB分别与⊙O相切于点A、B,
∴PA=PB=8,
设OM=x,则PN=8-x,PM=x,
在Rt△PMN中,∵MN2+PN2=PM2,
∴,
解得
即OM的长为
19.
(1)证明:连接OA,
∵AB⊥OP,OB=OA,
∴∠BOP=∠AOP,
∵PA是⊙O的切线,
∴∠OAP=90°,
在△OBP与△OAP中,
∴△OBP≌△OAP(SAS),
∴∠OBP=∠OAP=90°.
∴OB⊥PB.
∴PB是⊙O的切线;
(2)∵OD=5,OA=OB=3,∴在Rt△AOD中,AD==4,
∵PA、PB为⊙O的切线,
∴PA=PB,
在Rt△DBP中,PD2=PB2+BD2,即(PB+4)2=PB2+82,
解得,PB= 6,
在Rt△OBP中,OP==3.
20.
设切点分别为,,
(1)∵,,,
∴,
∵与△ADE各边所在直线都相切,
∴,,,
∴,即AN+AC=24,
∴,
∴EN=AN-AE=12-8=4,
连接,
∵ON⊥EN,ME⊥EN,OM⊥DE,OM=ON,
∴为正方形,
∴ON=EN=4,即的半径为4.
(2)连结,,,
∵,,
∴∠CDE=120°,∠DEN=90°,
∵与△ADE各边所在直线都相切,
∴∠CDO=∠MDO,∠MEO=∠NEO,
∴∠MDO=60°,∠MEO=45°,
∴∠DOE=180°-60°-45°=75°.
试卷第4页,共5页
试卷第5页,共5页
一、单选题
1.如图,PA、PB切⊙O于点A、B,PA=10,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( )
A.10 B.18 C.20 D.22
2.如图,是外一点,、切于点、,点在优弧上,若,则等于( )
A. B. C. D.
3.如图所示,半⊙O的直径在梯形ABCD的底边AB上,且与其余三边均相切,若BC=2,DA=3,则AB长为( )
A.4 B.5 C.6 D.不能确定
4.如图,点E为Rt△ABC的直角边AC上一点,以CE为直径的半圆与斜边AB相切于点D,连结DE.若∠B=70°,则∠CED为( )
A.70° B.65° C.55° D.35°
5.如图,PA、PB分别切⊙O于点A、B,且PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则PCD的周长为( )
A.32 B.24 C.16 D.8
6.如图,PA、PB切⊙O于点A、B,PA=4,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( )
A.4 B.8 C.12 D.16
7.如图,PA,PB是⊙O的切线,A,B是切点,若,则( )
A. B. C. D.
二、填空题
8.如图、、是圆的切线,切点分别为、、,若,,则的长是______.
9.如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D.若AB=8,AC=5,则BD的长是______.
10.如图,四边形中,、分别与以为直径的半圆切于点、,切半圆于点,若,,则 _____.
11.如图,⊙O的半径为2,直线PA、PB为⊙O的切线,A、B为切点,若PA⊥PB,则OP的长__.
12.如图,⊙I是RtABC的内切圆,∠C=90°,AC=6,BC=8,则⊙I的半径是_________.
13.如图,切线PA、PB分别与⊙O相切于点A、B,切线EF与⊙O相切于点C,且分别交PA、PB于点E、F,若△PEF的周长为12,则线段PA的长为 ___.
14.如图,,是的两条切线,切点分别为,.连接,,,,与交于点.若,,则的周长为______.
三、解答题
15.如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D.若AB=6,AC=4,求BD的长.
16.如图,是⊙的切线,切点为B,交⊙于点C,过点C的切线交于点D,若.求⊙的半径.
17.如图,已知,点A、B、C、D在圆上,.
(1)若EA、ED是的切线,切点分别是A、D,已知,求的周长;
(2)若,,,求BC的长.
18.如图,PA,PB分别与⊙O相切于点A,B.点M在PB上,且OMAP,,垂足为N.
(1)求证:OM=AN;
(2)若⊙O的半径R=4,PA=8,求OM的长.
19.如图,PA为⊙O的切线,A为切点,过点A作AB⊥OP,垂足为点C,交⊙O于点B,延长BO与PA的延长线交于点D.
(1)求证:PB为⊙O的切线;
(2)若OB=3,OD=5,求OP的长.
20.如图所示,与△ADE各边所在直线都相切,DE⊥AE.
(1)若AE=8,AD=10,求的半径;
(2)若∠EAD=30°,求∠DOE.
参考答案
1.C
解:∵PA、PB切⊙O于点A、B,CD切⊙O于点E,
∴PA=PB=10,CA=CE,DE=DB,
∴△PCD的周长是PC+CD+PD
=PC+AC+DB+PD
=PA+PB
=10+10
=20.
故选:C.
2.C
解:、都为圆的切线,
,
,
,
与都对,
.
故选:.
3.B
解:如图,
连接OC,OD,设⊙O的半径为r,
∵BC、CD、DA与半⊙O相切,
∴在△AOD中,AD边上的高和AO边上的高都为r,
∴AO=AD,
同理BO=BC,
∴AB=AO+BO=AD+BC=2+3=5.
故选:B.
4.C
解:连接,
∵,
∴与半圆相切与点,
∵半圆与斜边AB相切于点D,
∴,
∵∠B=70°,
∴,
∴,
∵CE为直径,
∴,
∴∠CED,
故选:C.
5.C
解:∵PA、PB切⊙O于点A、B,
∴PB=PA=8,
∵CD切⊙O于点E,交PA、PB于C、D两点,
∴CA=CE,DB=DE,
∴PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=8+8=16.
则△PCD的周长是16.
故选C.
6.B
解:∵PA、PB切⊙O于点A、B,
∴PB=PA=4,
∵CD切⊙O于点E,交PA、PB于C、D两点,
∴CA=CE,DB=DE,
∴PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=4+4=8.
则△PCD的周长是8.
故选:B.
7.B
解:PA,PB是⊙O的切线,
故选:B.
8.3
解:∵AB、AC、BD是圆O的切线,
∴AC=AP,BP=BD=2,
∵AP=AB﹣BP=5﹣2=3,
∴AC=3.
故答案为3.
9.3
解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB AP=8 5=3.
故答案为:3.
10.6
解:、和都是半圆的切线,
由切线长定理得:
,,
,
,,
,
故答案为6.
11.
解:连接OA,
∵直线PA、PB为⊙O的切线,PA⊥PB,
∴OA⊥PA,∠OPA=∠APB=45°,
∴△OPA是等腰直角三角形,
∵⊙O的半径为2,
即OA=2,
∴OP=OA=2.
故答案为:.
12.2
解:如图,连接,,
在中,
,,,
,
⊙I是RtABC的内切圆,
∴,
在四边形中,
,,
四边形是正方形,
设,
由切线长定理得:,,
∵AC=6,BC=8,
∴,,
又∵,
∴,
解得:,
∴⊙I的半径是2,
故答案为:2.
13.6
解:∵切线EF与⊙O相切于点C,且分别交PA、PB于点E、F,
∴EA=EC,FC=FB,
∵△PEF的周长=PE+EF+PF=12,
∴PE+EA+FB+PF=12,
∴PA+PB=12,
又∵切线PA、PB分别与⊙O相切于点A、B,
∴PA=PB=6.
故答案为:6.
14.
解:∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,AB=2AC,PO⊥AB,
∴∠PAB=60°,
∴∠OAC=∠PAO-∠PAB=90°-60°=30°,
∴AO=2OC,
∵OC=1,
∴AO=2,
∴AC=,
∴AB=2AC=,
∴△PAB的周长=.
故答案为:.
15.2
解:∵AB、AC、BD是⊙O的切线,切点分别为P、C、D,
∴AC=AP,BP=BD,
∴BD=BP=AB AP== AB AC= 6 4=2.
16.
连接,
∵都是的切线,
∴,且,
∴,
∴,
在中,可求得,
设半径为r,则,
在中,由勾股定理可得:,
即,
解得,
∴的半径是.
17.(1)26;(2)
解:(1)∵EA、ED是的切线,,
∴,
又∵,
∴的周长;
(2),,,
∴,
∴∠ADC=90°,
∵四边形ABCD是圆的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ABC=90°,
又∵,
∴.
18.
(1)证明:连接OA,如图, ∵PA为⊙O的切线,
∴OA⊥PA, ∴∠OAP=90°,
∵ ,
∴∠AOM=90°, 而MN⊥PA,
∴∠MNA=90°,
∴四边形ANMO为矩形,
∴OM=AN;
(2)解:连接OB,如图,
∵PB为⊙O的切线, ∴OB⊥PB,OB=4,
∴∠OBM=90°,
∵四边形ANMO为矩形,
∴MN=OA=4,OM=AN,
∴OB=MN,
∵, ∴∠MPN=∠BMO,
在△PMN和△MOB中,
,
∴△PMN≌△MOB(AAS),
∴PM=OM,
∴OM=AN=PM,
∵PA、PB分别与⊙O相切于点A、B,
∴PA=PB=8,
设OM=x,则PN=8-x,PM=x,
在Rt△PMN中,∵MN2+PN2=PM2,
∴,
解得
即OM的长为
19.
(1)证明:连接OA,
∵AB⊥OP,OB=OA,
∴∠BOP=∠AOP,
∵PA是⊙O的切线,
∴∠OAP=90°,
在△OBP与△OAP中,
∴△OBP≌△OAP(SAS),
∴∠OBP=∠OAP=90°.
∴OB⊥PB.
∴PB是⊙O的切线;
(2)∵OD=5,OA=OB=3,∴在Rt△AOD中,AD==4,
∵PA、PB为⊙O的切线,
∴PA=PB,
在Rt△DBP中,PD2=PB2+BD2,即(PB+4)2=PB2+82,
解得,PB= 6,
在Rt△OBP中,OP==3.
20.
设切点分别为,,
(1)∵,,,
∴,
∵与△ADE各边所在直线都相切,
∴,,,
∴,即AN+AC=24,
∴,
∴EN=AN-AE=12-8=4,
连接,
∵ON⊥EN,ME⊥EN,OM⊥DE,OM=ON,
∴为正方形,
∴ON=EN=4,即的半径为4.
(2)连结,,,
∵,,
∴∠CDE=120°,∠DEN=90°,
∵与△ADE各边所在直线都相切,
∴∠CDO=∠MDO,∠MEO=∠NEO,
∴∠MDO=60°,∠MEO=45°,
∴∠DOE=180°-60°-45°=75°.
试卷第4页,共5页
试卷第5页,共5页
同课章节目录
