【人教八上数学教学课件】15.2.1 第1课时 分式的乘除 课件(共22张PPT)
文档属性
| 名称 | 【人教八上数学教学课件】15.2.1 第1课时 分式的乘除 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 09:07:49 | ||
图片预览








文档简介
(共22张PPT)
第十五章 分式
15.2.1 第1课时 分式的乘除
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
问题1 一个长方体容器的容积为V,底面的长为a,宽为b,当容器内的水占容积的 时,水高多少
长方体容器的高为 ,
水高为
问题2 大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,大拖拉机的工作效率是小拖拉机的工作效率的多少倍
大拖拉机的工作效率是 公顷/天,小拖拉机的
工作效率是 公顷/天,大拖拉机的工作效率
是小拖拉机的工作效率的( )倍.
获取新知
知识点一:分式的乘除
思考:
你还记得分数的乘除法法则吗?
类比分数的乘除法法则,你能说出分式的乘除法法则吗?
想一想:
知识要点
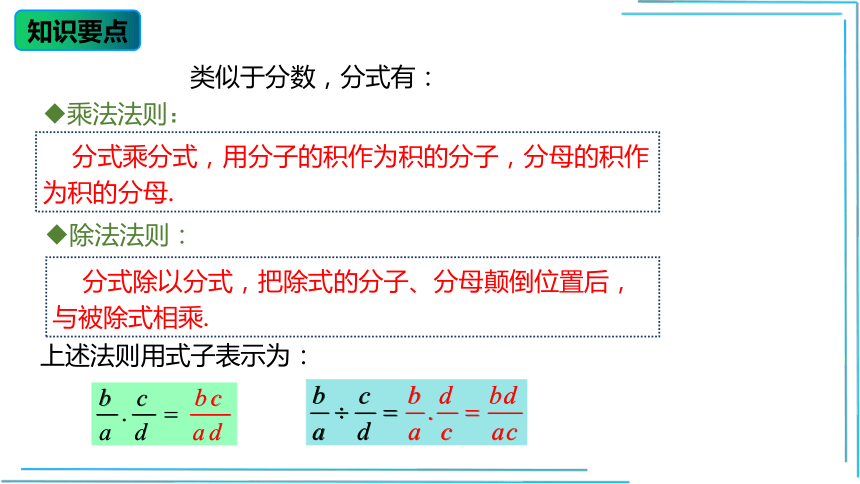
类似于分数,分式有:
乘法法则:
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
除法法则:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
上述法则用式子表示为:
例题讲解
例1 计算:
解:
先把除法转化为乘法
约分
注意:按照法则进行分式乘除运算,如果运算结果不是最简分式,一定要进行约分,使运算结果化成最简分式.
例2 计算:
解:原式=
(1)
分子、分母是多项式时,先分解因式 便于约分.
约分
解:原式=
先把除法转化为乘法.
整式与分式 运算时,可以把整式看成分母是1的分式.
负号怎么得来的?
归纳总结
计算分式乘除的一般步骤:
(1)分解因式:将分式的分子、分母中的多项式分解因式;
(2)化除为乘:将除法转化为乘法并计算;
(3)约分:将所得结果的分子、分母中相同的因式进行约分;
(4)整理结果:将分式的分子、分母中剩下的因式分别相乘,
并整理出最后结果.
注意:若分式的乘除运算中出现了整式,可以把整式看作“分
母为1”的式子进行计算.
例3 “丰收1号”小麦的试验田是边长为a米的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a-1)米的正方形,两块试验田的小麦都收获了500千克.
(1)哪种小麦的单位面积产量高?
(2)高的单位面积产量是低的单位面积产量的多少倍?
1m
am
(a-1)m
am
1m
(a-1)m
∵a>1, 0<(a-1)2, a 2-1>0,
由图可得(a-1)2< a 2-1.
∴
解:(1)“丰收1号”小麦的试验田面积是(a 2-1)m2,单位面积产量是 kg/m2;“丰收2号”小麦的试验田面积是(a-1)2m2,单位面积产量是 kg/m2.
∴“丰收2号”小麦的单位面积产量高.
(2)
所以 “丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的 倍.
知识点二:分式的乘除混合运算
例1
解析:先将除法变为乘法,再根据分式的乘法运算法则进行运算.
=(a-2)(a+1)=a2-a-2.
分式乘除混合运算的一般步骤
(1)先把除法统一成乘法运算;
(3)确定分式的符号,然后约分;
(4)结果应是最简分式.
(2)分子、分母中能分解因式的多项式分解因式;
解:原式=
练一练
计算:
随堂演练
1.计算 等于( )
A. B. C. D.
C
2.化简 的结果是( )
B
解:(1)原式
(2)原式
(1)
(2)
3.计算
解析:利用分式的乘法法则先进行计算化简,然后代入求值.
4.先化简,再求值:
课堂小结
分式乘除运算
乘除法运算
注意
(1)分子分母是单项式的,先按法则进行,再约分化成最简分式或整式
除法先转化成乘法,再按照乘法法则进行运算
(2)分子分母是多项式的,通常要先分解因式再按法则进行
(3)运用法则时要注意符号的变化
乘除法法则
https://www.21cnjy.com/help/help_extract.php
第十五章 分式
15.2.1 第1课时 分式的乘除
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
问题1 一个长方体容器的容积为V,底面的长为a,宽为b,当容器内的水占容积的 时,水高多少
长方体容器的高为 ,
水高为
问题2 大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,大拖拉机的工作效率是小拖拉机的工作效率的多少倍
大拖拉机的工作效率是 公顷/天,小拖拉机的
工作效率是 公顷/天,大拖拉机的工作效率
是小拖拉机的工作效率的( )倍.
获取新知
知识点一:分式的乘除
思考:
你还记得分数的乘除法法则吗?
类比分数的乘除法法则,你能说出分式的乘除法法则吗?
想一想:
知识要点
类似于分数,分式有:
乘法法则:
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
除法法则:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
上述法则用式子表示为:
例题讲解
例1 计算:
解:
先把除法转化为乘法
约分
注意:按照法则进行分式乘除运算,如果运算结果不是最简分式,一定要进行约分,使运算结果化成最简分式.
例2 计算:
解:原式=
(1)
分子、分母是多项式时,先分解因式 便于约分.
约分
解:原式=
先把除法转化为乘法.
整式与分式 运算时,可以把整式看成分母是1的分式.
负号怎么得来的?
归纳总结
计算分式乘除的一般步骤:
(1)分解因式:将分式的分子、分母中的多项式分解因式;
(2)化除为乘:将除法转化为乘法并计算;
(3)约分:将所得结果的分子、分母中相同的因式进行约分;
(4)整理结果:将分式的分子、分母中剩下的因式分别相乘,
并整理出最后结果.
注意:若分式的乘除运算中出现了整式,可以把整式看作“分
母为1”的式子进行计算.
例3 “丰收1号”小麦的试验田是边长为a米的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a-1)米的正方形,两块试验田的小麦都收获了500千克.
(1)哪种小麦的单位面积产量高?
(2)高的单位面积产量是低的单位面积产量的多少倍?
1m
am
(a-1)m
am
1m
(a-1)m
∵a>1, 0<(a-1)2, a 2-1>0,
由图可得(a-1)2< a 2-1.
∴
解:(1)“丰收1号”小麦的试验田面积是(a 2-1)m2,单位面积产量是 kg/m2;“丰收2号”小麦的试验田面积是(a-1)2m2,单位面积产量是 kg/m2.
∴“丰收2号”小麦的单位面积产量高.
(2)
所以 “丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的 倍.
知识点二:分式的乘除混合运算
例1
解析:先将除法变为乘法,再根据分式的乘法运算法则进行运算.
=(a-2)(a+1)=a2-a-2.
分式乘除混合运算的一般步骤
(1)先把除法统一成乘法运算;
(3)确定分式的符号,然后约分;
(4)结果应是最简分式.
(2)分子、分母中能分解因式的多项式分解因式;
解:原式=
练一练
计算:
随堂演练
1.计算 等于( )
A. B. C. D.
C
2.化简 的结果是( )
B
解:(1)原式
(2)原式
(1)
(2)
3.计算
解析:利用分式的乘法法则先进行计算化简,然后代入求值.
4.先化简,再求值:
课堂小结
分式乘除运算
乘除法运算
注意
(1)分子分母是单项式的,先按法则进行,再约分化成最简分式或整式
除法先转化成乘法,再按照乘法法则进行运算
(2)分子分母是多项式的,通常要先分解因式再按法则进行
(3)运用法则时要注意符号的变化
乘除法法则
https://www.21cnjy.com/help/help_extract.php
