【人教八上数学教学课件】15.2.3 第1课时 负整数指数幂 课件(共21张PPT)
文档属性
| 名称 | 【人教八上数学教学课件】15.2.3 第1课时 负整数指数幂 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 09:20:52 | ||
图片预览








文档简介
(共21张PPT)
第十五章 分式
15.2.3 第1课时 负整数指数幂
随堂演练
获取新知
知识回顾
例题讲解
课堂小结
知识回顾
算一算,并分别说出每一小题所用的运算性质.
(2) = ;
同底数幂的乘法:
(m,n是正整数)
幂的乘方:
(m,n是正整数)
(3) = ;
积的乘方:
(n是正整数)
(4) = ;
同底数幂的除法:
(a≠0,m,n是正整数且m>n )
乘方:
(b≠0,n是正整数)
(6) = ;
(5) = ;
( )
获取新知
想一想:
am中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
问题:计算:a3 ÷a5= (a ≠0)
解法1
解法2 再假设正整数指数幂的运算性质am÷an=am-n(a≠0,m,n是正整数,m>n)中的m>n这个条件去掉,那么a3÷a5=a3-5=a-2.
于是得到:
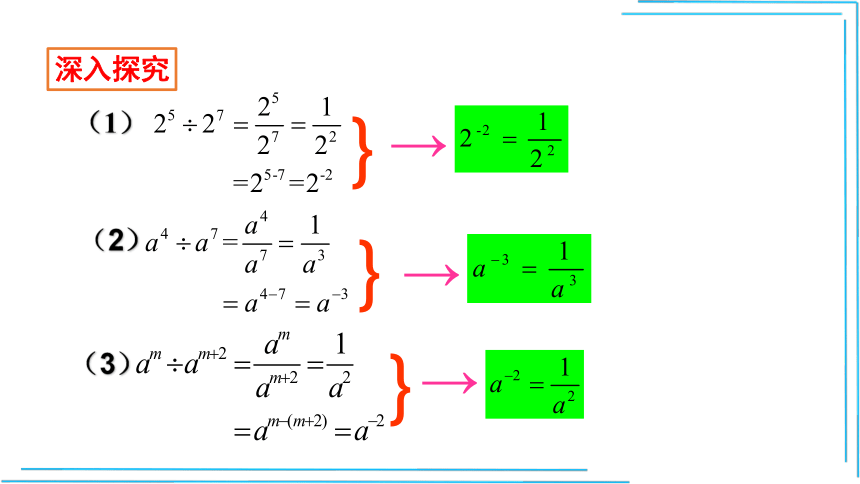
(3)
→
}
}
}
→
→
(1)
(2)
深入探究
知识要点
负整数指数幂的意义
一般地,我们规定:当n是正整数时,
这就是说,a-n (a≠0)是an的倒数.
你能猜出:
当m分别是正整数、0 、负整数时,am分别表示什么意思吗?
引入负整数指数幂后,指数的取值范围就扩大到全体整数。
am=
am (m是正整数)
1 (m=0)
(m是负整数)
(1)32=___, 30=___, 3-2=_____;
(2)(-3)2=__,(-3)0=___,(-3)-2=_____;
(3)b2=___, b0=____, b-2=____(b≠0).
练 习
9
1
9
1
1
b2
1
9
1
9
1
b2
例题讲解
例1
A.a>b=c B.a>c>b
C.c>a>b D.b>c>a
B
方法总结:关键是理解负整数指数幂的意义,依次计算出结果.当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
例2
解析:先进行幂的乘方,再进行幂的乘除,最后将整数指数幂化成正整数指数幂.
解:(1)原式=x6y-4
(2)原式=x2y-2·x-6y3=x-4y
提示:计算结果一般需化为正整数幂的形式.
计算:
(1)(x3y-2)2; (2)x2y-2·(x-2y)3;
计算:
(3)(3x2y-2)2÷(x-2y)3; (4)(3×10-5)3÷(3×10-6)2.
例2
=(27×10-15)÷(9×10-12)
=3×10-3
解:=9x4y-4÷x-6y3
=9x4y-4·x6y-3
=9x10y-7
计算:
解:
练一练
解:
(1) 根据整数指数幂的运算性质,当m,n为整数时,
am ÷an=am-n
又am ·a-n=am-n,因此am ÷an=am ·a-n.
即同底数幂的除法可以转化为同底数幂的乘法.
(2) 特别地,
所以
即商的乘方可以转化为积的乘方.
总结归纳
整数指数幂的运算性质归结为
(1)am·an=am+n ( m、n是整数) ;
(2)(am)n=amn ( m、n是整数) ;
(3)(ab)n=anbn ( n是整数).
随堂演练
1.填空:(-3)2·(-3)-2=( );103×10-2=( );
a-2÷a3=( );a3÷a-4=( ).
2.计算:(1)0.1÷0.13
(2)(-5)2 008÷(-5)2 010
(3)100×10-1÷10-2
(4)x-2·x-3÷x2
1
10
a7
课堂小结
整数
指数幂
负整数指数幂:当n是正整数时,a-n=
整数指数幂的运算性质:
(1)am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
https://www.21cnjy.com/help/help_extract.php
第十五章 分式
15.2.3 第1课时 负整数指数幂
随堂演练
获取新知
知识回顾
例题讲解
课堂小结
知识回顾
算一算,并分别说出每一小题所用的运算性质.
(2) = ;
同底数幂的乘法:
(m,n是正整数)
幂的乘方:
(m,n是正整数)
(3) = ;
积的乘方:
(n是正整数)
(4) = ;
同底数幂的除法:
(a≠0,m,n是正整数且m>n )
乘方:
(b≠0,n是正整数)
(6) = ;
(5) = ;
( )
获取新知
想一想:
am中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
问题:计算:a3 ÷a5= (a ≠0)
解法1
解法2 再假设正整数指数幂的运算性质am÷an=am-n(a≠0,m,n是正整数,m>n)中的m>n这个条件去掉,那么a3÷a5=a3-5=a-2.
于是得到:
(3)
→
}
}
}
→
→
(1)
(2)
深入探究
知识要点
负整数指数幂的意义
一般地,我们规定:当n是正整数时,
这就是说,a-n (a≠0)是an的倒数.
你能猜出:
当m分别是正整数、0 、负整数时,am分别表示什么意思吗?
引入负整数指数幂后,指数的取值范围就扩大到全体整数。
am=
am (m是正整数)
1 (m=0)
(m是负整数)
(1)32=___, 30=___, 3-2=_____;
(2)(-3)2=__,(-3)0=___,(-3)-2=_____;
(3)b2=___, b0=____, b-2=____(b≠0).
练 习
9
1
9
1
1
b2
1
9
1
9
1
b2
例题讲解
例1
A.a>b=c B.a>c>b
C.c>a>b D.b>c>a
B
方法总结:关键是理解负整数指数幂的意义,依次计算出结果.当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
例2
解析:先进行幂的乘方,再进行幂的乘除,最后将整数指数幂化成正整数指数幂.
解:(1)原式=x6y-4
(2)原式=x2y-2·x-6y3=x-4y
提示:计算结果一般需化为正整数幂的形式.
计算:
(1)(x3y-2)2; (2)x2y-2·(x-2y)3;
计算:
(3)(3x2y-2)2÷(x-2y)3; (4)(3×10-5)3÷(3×10-6)2.
例2
=(27×10-15)÷(9×10-12)
=3×10-3
解:=9x4y-4÷x-6y3
=9x4y-4·x6y-3
=9x10y-7
计算:
解:
练一练
解:
(1) 根据整数指数幂的运算性质,当m,n为整数时,
am ÷an=am-n
又am ·a-n=am-n,因此am ÷an=am ·a-n.
即同底数幂的除法可以转化为同底数幂的乘法.
(2) 特别地,
所以
即商的乘方可以转化为积的乘方.
总结归纳
整数指数幂的运算性质归结为
(1)am·an=am+n ( m、n是整数) ;
(2)(am)n=amn ( m、n是整数) ;
(3)(ab)n=anbn ( n是整数).
随堂演练
1.填空:(-3)2·(-3)-2=( );103×10-2=( );
a-2÷a3=( );a3÷a-4=( ).
2.计算:(1)0.1÷0.13
(2)(-5)2 008÷(-5)2 010
(3)100×10-1÷10-2
(4)x-2·x-3÷x2
1
10
a7
课堂小结
整数
指数幂
负整数指数幂:当n是正整数时,a-n=
整数指数幂的运算性质:
(1)am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
https://www.21cnjy.com/help/help_extract.php
