27.2.2相似三角形的性质 课件(共30张PPT)
文档属性
| 名称 | 27.2.2相似三角形的性质 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 10:06:14 | ||
图片预览





文档简介
(共30张PPT)
27.2.2相似三角形的性质
人教版 九年级下
教学目标
1.理解并掌握相似三角形中对应线段的比、相似三角形的面积比与相似比的关系.(重点、难点)
2.学会运用相似三角形中对应线段的比、相似三角形的面积比与相似比的关系解决问题.(重点)
回顾旧知
问题1:什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
问题2:如何判定两个三角形相似?
①定义;
②平行于三角形一边,与另外两边相交所构成的三角形与原
三角形相似;
③ 三边成比例的两个三角形相似
④两个角对应相等的两个三角形相似;
⑤两边对应成比例,且夹角相等的两个三角形相似;
对于直角三角形还有第6种判定方法:一条直角边和斜边对应成比例的两直角三角形相似!
合作探究
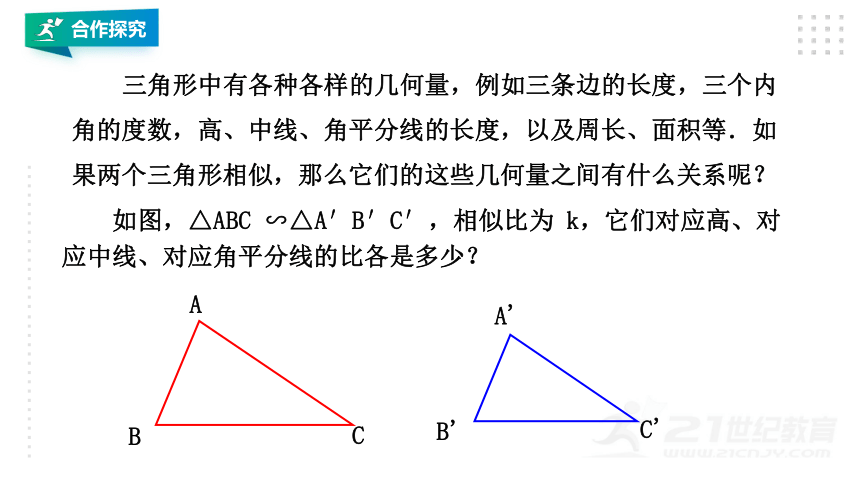
三角形中有各种各样的几何量,例如三条边的长度,三个内角的度数,高、中线、角平分线的长度,以及周长、面积等.如果两个三角形相似,那么它们的这些几何量之间有什么关系呢?
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
合作探究
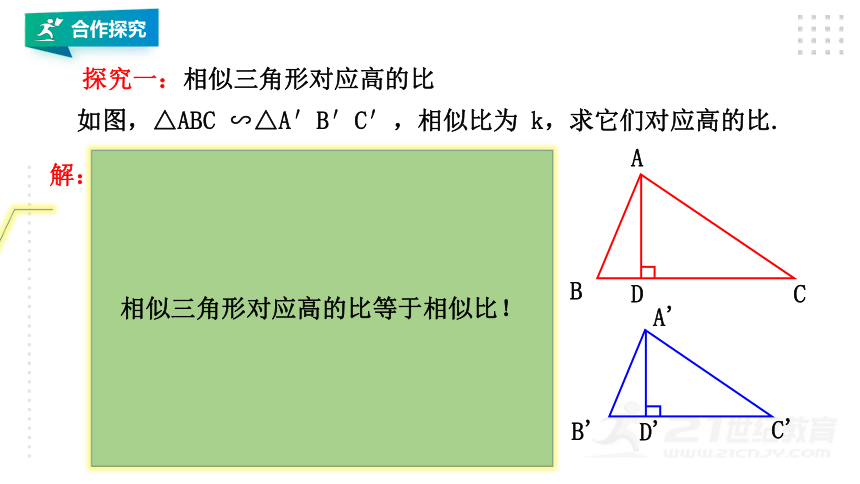
探究一:相似三角形对应高的比
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出 △ABC 和△A‘ B’ C‘
的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应高的比.
相似三角形对应高的比等于相似比!
合作探究
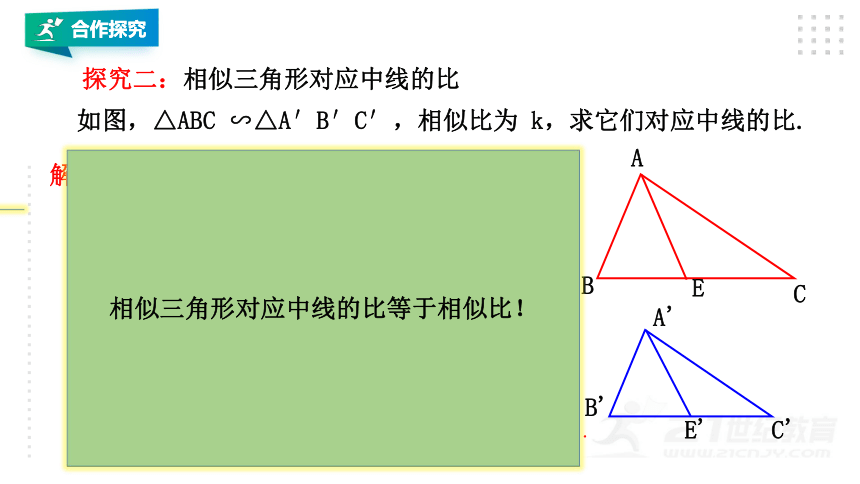
探究二:相似三角形对应中线的比
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应中线的比.
合作探究
∵△ABC ∽△A′B′C′,
∴∠B=∠B′ ,
解:如图,分别作出 △ABC 和△A′B′C′
的中线 AE 和 A′ E′ .
则BE = B′E′=
∴△ABE ∽△A′ B′E′
A
B
C
A'
B'
C'
E'
E
∴
∴
相似三角形对应中线的比等于相似比!
合作探究
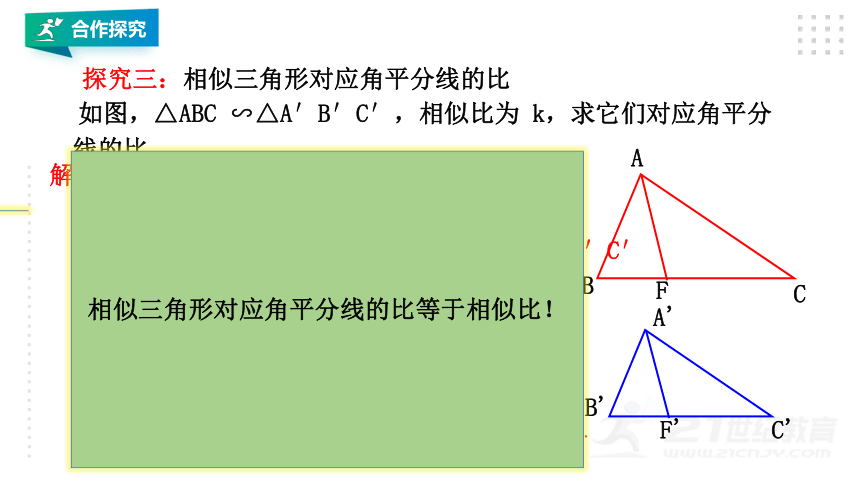
探究三:相似三角形对应角平分线的比
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应角平分
线的比.
∵△ABC ∽△A′B′C′,
∴∠B=∠B′ , ∠BAC= ∠B′A′C ′
解:如图,分别作出 △ABC 和△A′B′C′
的对应角平分线 AF 和 A′F′ .
则∠BAF= ∠BAC, ∠B′A′F ′= ∠B′A′C′
∴△ABF ∽△A′ B′F′
A
B
C
A'
B'
C'
F'
F
∴
∴∠BAF= ∠B′A′F ′
相似三角形对应角平分线的比等于相似比!
合作探究
相似三角形对应中线的比等于相似比.
相似三角形对应角平分线的比等于相似比.
相似三角形对应高的比等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
归纳总结:
趁热打铁
1、如果两个相似三角形的对应高的比为 4 : 5,那么对应角平分线的比是 ,对应边上的中线的比是______ .
2、已知△ABC ∽ △A'B'C' ,相似比为1 : 3,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =______ .
4 : 5
4 : 5
36 cm
3、已知△ABC∽△DEF,若△ABC与△DEF的相似比为 ,则△ABC与△DEF对应中线的比为______ .
趁热打铁
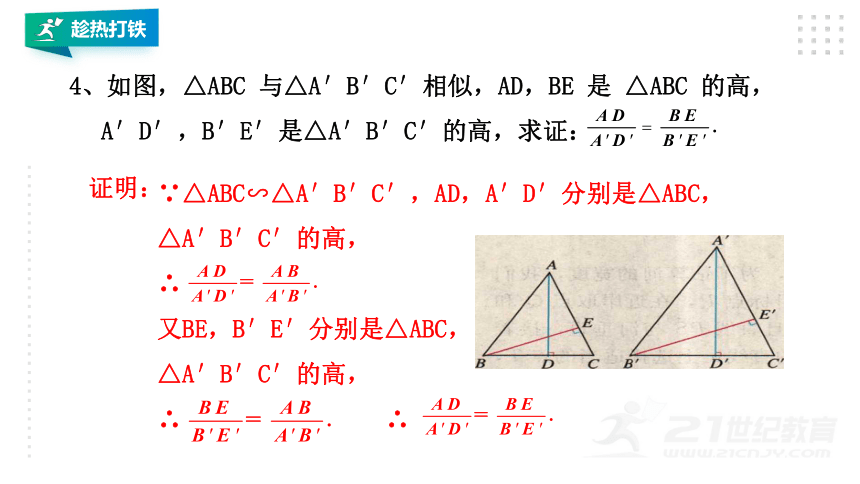
4、如图,△ABC 与△A′B′C′相似,AD,BE 是 △ABC 的高,A′D′,B′E′是△A′B′C′的高,求证:
∵△ABC∽△A′B′C′,AD,A′D′分别是△ABC,△A′B′C′的高,
∴
又BE,B′E′分别是△ABC,
△A′B′C′的高,
∴ ∴
证明:
趁热打铁
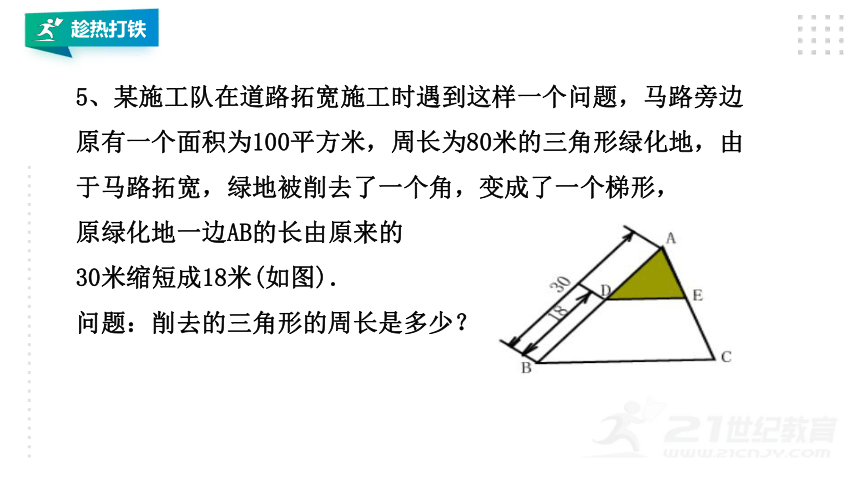
5、某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽,绿地被削去了一个角,变成了一个梯形,
原绿化地一边AB的长由原来的
30米缩短成18米(如图).
问题:削去的三角形的周长是多少?
趁热打铁
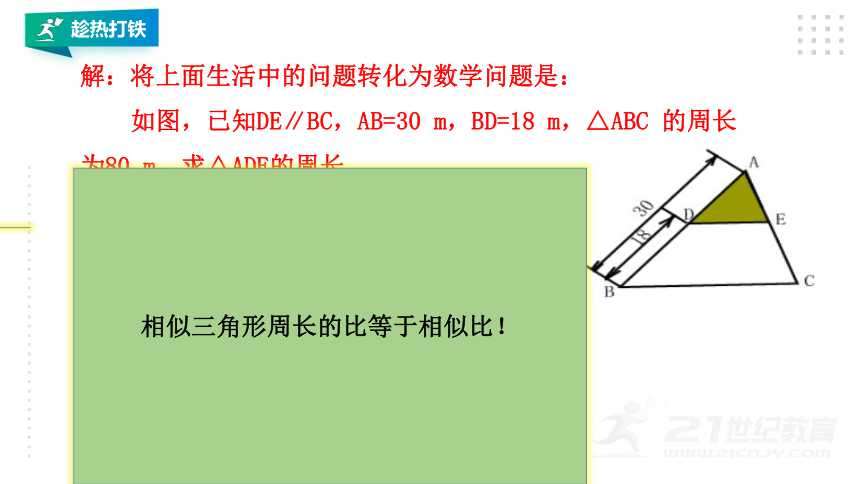
解:将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30 m,BD=18 m,△ABC 的周长为80 m,求△ADE的周长.
∵DE∥BC,
∴△ADE∽△ABC,∴
由比例的性质可得:
而△ADE 的周长=AD+AE+DE,
△ABC的周长=AB+AC+BC,
∴
∴△ADE 的周长=32 m.
相似三角形周长的比等于相似比!
合作探究
探究四:相似三角形面积的比
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
合作探究
由前面的结论,我们有:
A
B
C
A'
B'
C'
D'
D
相似三角形面积的比等于相似比的平方!
典例精析
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为
A
B
C
D
E
F
∴
例1、如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
典例精析
A
B
C
D
E
F
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
综合演练
1. 判断:
(1) 一个三角形的各边长扩大为原来的5倍,这个
三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的6倍,这个
三角形的周长也扩大为原来的6倍; ( )
(3)一个三角形的各边长扩大为原来的9倍,这个
三角形的面积也扩大为原来的9倍 ( )
√
×
√
综合演练
2、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC的周长之比为( )
A.1:2 B.1:3
C.1:4 D.1:5
A
3、已知△ABC∽△DEF,AB∶DE=1∶2,则下列等式一定成立的是( )
A. B.
C. D.
D
综合演练
4、有3个正方形按如图所示放置,阴影部分的面积依次记为S1,S2,则S1: S2等于( )
A.1:
B.1:2
C.2:3
D.4:9
D
5、如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,AE,CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A.1:3 B.1:4
C.1:5 D. 1:25
B
综合演练
6、如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① ②S△BCE=36;③S△ABE=12;④△AEF∽△ACD.其中一定正确的是
( )
A.①②③④
B.①④
C.②③④
D.①②③
D
综合演练
7、如果两个相似三角形的面积之比为 2 : 7,较大三角形一边上的高为 7,则较小三角形对应边上的高为______.
8、连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_____.
1 : 2
1 : 4
9、两个相似三角形对应的中线长分别是 6 cm 和 18 cm, 若较大三角形的周长是 42 cm,面积是 12 cm2,则较小三角形的周长____cm,面积为____cm2.
14
综合演练
10、如图,D、E分别是AC、AB上的点,已知△ABC的面积为100 cm2,
且 ,求四边形BCDE的面积.
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
综合演练
11、如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
∴ △ADE ∽ △ABC ,
即相似比为 1 : 2,
面积比为 1 : 4.
∴
综合演练
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 ,
∴面积比为 1 : 4.
设 S△ABC = 4a,则 S△ADE = a,S△EFC = a,
S四边形BFED = S△ABC-S△ADE-S△EFC = 4a-a-a= 2a,
∴ S四边形BFED : S△ABC = 2a : 4a =
提能训练
12、如图,在△ABC中,AD是BC边上的高,矩形EFGH内接于三角形ABC,且长边FG在BC上,矩形相邻两边的比为1∶2,若BC=30 cm,AD=10 cm,求矩形EFGH的周长.
提能训练
解:设HG=x cm,则EH=2x cm. 易得AP⊥EH.
∵AD=10 cm,∴AP=(10-x) cm.
∵四边形EFGH为矩形,∴EH∥BC,
∴△AEH ∽ △ABC.∴
解得x=6.∴HG=6 cm,EH=12 cm.
∴矩形EFGH的周长为36 cm.
课堂总结
说一说:
1、相似三角形中哪些对应线段的比等于相似比?
2、相似三角形的面积比与相似比有什么关系?
本节课你有哪些收获?
作业布置
P39页:练习:3
https://www.21cnjy.com/help/help_extract.php
27.2.2相似三角形的性质
人教版 九年级下
教学目标
1.理解并掌握相似三角形中对应线段的比、相似三角形的面积比与相似比的关系.(重点、难点)
2.学会运用相似三角形中对应线段的比、相似三角形的面积比与相似比的关系解决问题.(重点)
回顾旧知
问题1:什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
问题2:如何判定两个三角形相似?
①定义;
②平行于三角形一边,与另外两边相交所构成的三角形与原
三角形相似;
③ 三边成比例的两个三角形相似
④两个角对应相等的两个三角形相似;
⑤两边对应成比例,且夹角相等的两个三角形相似;
对于直角三角形还有第6种判定方法:一条直角边和斜边对应成比例的两直角三角形相似!
合作探究
三角形中有各种各样的几何量,例如三条边的长度,三个内角的度数,高、中线、角平分线的长度,以及周长、面积等.如果两个三角形相似,那么它们的这些几何量之间有什么关系呢?
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
合作探究
探究一:相似三角形对应高的比
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出 △ABC 和△A‘ B’ C‘
的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应高的比.
相似三角形对应高的比等于相似比!
合作探究
探究二:相似三角形对应中线的比
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应中线的比.
合作探究
∵△ABC ∽△A′B′C′,
∴∠B=∠B′ ,
解:如图,分别作出 △ABC 和△A′B′C′
的中线 AE 和 A′ E′ .
则BE = B′E′=
∴△ABE ∽△A′ B′E′
A
B
C
A'
B'
C'
E'
E
∴
∴
相似三角形对应中线的比等于相似比!
合作探究
探究三:相似三角形对应角平分线的比
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应角平分
线的比.
∵△ABC ∽△A′B′C′,
∴∠B=∠B′ , ∠BAC= ∠B′A′C ′
解:如图,分别作出 △ABC 和△A′B′C′
的对应角平分线 AF 和 A′F′ .
则∠BAF= ∠BAC, ∠B′A′F ′= ∠B′A′C′
∴△ABF ∽△A′ B′F′
A
B
C
A'
B'
C'
F'
F
∴
∴∠BAF= ∠B′A′F ′
相似三角形对应角平分线的比等于相似比!
合作探究
相似三角形对应中线的比等于相似比.
相似三角形对应角平分线的比等于相似比.
相似三角形对应高的比等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
归纳总结:
趁热打铁
1、如果两个相似三角形的对应高的比为 4 : 5,那么对应角平分线的比是 ,对应边上的中线的比是______ .
2、已知△ABC ∽ △A'B'C' ,相似比为1 : 3,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =______ .
4 : 5
4 : 5
36 cm
3、已知△ABC∽△DEF,若△ABC与△DEF的相似比为 ,则△ABC与△DEF对应中线的比为______ .
趁热打铁
4、如图,△ABC 与△A′B′C′相似,AD,BE 是 △ABC 的高,A′D′,B′E′是△A′B′C′的高,求证:
∵△ABC∽△A′B′C′,AD,A′D′分别是△ABC,△A′B′C′的高,
∴
又BE,B′E′分别是△ABC,
△A′B′C′的高,
∴ ∴
证明:
趁热打铁
5、某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽,绿地被削去了一个角,变成了一个梯形,
原绿化地一边AB的长由原来的
30米缩短成18米(如图).
问题:削去的三角形的周长是多少?
趁热打铁
解:将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30 m,BD=18 m,△ABC 的周长为80 m,求△ADE的周长.
∵DE∥BC,
∴△ADE∽△ABC,∴
由比例的性质可得:
而△ADE 的周长=AD+AE+DE,
△ABC的周长=AB+AC+BC,
∴
∴△ADE 的周长=32 m.
相似三角形周长的比等于相似比!
合作探究
探究四:相似三角形面积的比
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
合作探究
由前面的结论,我们有:
A
B
C
A'
B'
C'
D'
D
相似三角形面积的比等于相似比的平方!
典例精析
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为
A
B
C
D
E
F
∴
例1、如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
典例精析
A
B
C
D
E
F
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
综合演练
1. 判断:
(1) 一个三角形的各边长扩大为原来的5倍,这个
三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的6倍,这个
三角形的周长也扩大为原来的6倍; ( )
(3)一个三角形的各边长扩大为原来的9倍,这个
三角形的面积也扩大为原来的9倍 ( )
√
×
√
综合演练
2、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC的周长之比为( )
A.1:2 B.1:3
C.1:4 D.1:5
A
3、已知△ABC∽△DEF,AB∶DE=1∶2,则下列等式一定成立的是( )
A. B.
C. D.
D
综合演练
4、有3个正方形按如图所示放置,阴影部分的面积依次记为S1,S2,则S1: S2等于( )
A.1:
B.1:2
C.2:3
D.4:9
D
5、如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,AE,CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A.1:3 B.1:4
C.1:5 D. 1:25
B
综合演练
6、如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① ②S△BCE=36;③S△ABE=12;④△AEF∽△ACD.其中一定正确的是
( )
A.①②③④
B.①④
C.②③④
D.①②③
D
综合演练
7、如果两个相似三角形的面积之比为 2 : 7,较大三角形一边上的高为 7,则较小三角形对应边上的高为______.
8、连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_____.
1 : 2
1 : 4
9、两个相似三角形对应的中线长分别是 6 cm 和 18 cm, 若较大三角形的周长是 42 cm,面积是 12 cm2,则较小三角形的周长____cm,面积为____cm2.
14
综合演练
10、如图,D、E分别是AC、AB上的点,已知△ABC的面积为100 cm2,
且 ,求四边形BCDE的面积.
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
综合演练
11、如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
∴ △ADE ∽ △ABC ,
即相似比为 1 : 2,
面积比为 1 : 4.
∴
综合演练
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 ,
∴面积比为 1 : 4.
设 S△ABC = 4a,则 S△ADE = a,S△EFC = a,
S四边形BFED = S△ABC-S△ADE-S△EFC = 4a-a-a= 2a,
∴ S四边形BFED : S△ABC = 2a : 4a =
提能训练
12、如图,在△ABC中,AD是BC边上的高,矩形EFGH内接于三角形ABC,且长边FG在BC上,矩形相邻两边的比为1∶2,若BC=30 cm,AD=10 cm,求矩形EFGH的周长.
提能训练
解:设HG=x cm,则EH=2x cm. 易得AP⊥EH.
∵AD=10 cm,∴AP=(10-x) cm.
∵四边形EFGH为矩形,∴EH∥BC,
∴△AEH ∽ △ABC.∴
解得x=6.∴HG=6 cm,EH=12 cm.
∴矩形EFGH的周长为36 cm.
课堂总结
说一说:
1、相似三角形中哪些对应线段的比等于相似比?
2、相似三角形的面积比与相似比有什么关系?
本节课你有哪些收获?
作业布置
P39页:练习:3
https://www.21cnjy.com/help/help_extract.php
