六年级数学下册课件-5 数学广角—鸽巢问题 -人教版(共20张PPT)
文档属性
| 名称 | 六年级数学下册课件-5 数学广角—鸽巢问题 -人教版(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1017.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 07:21:38 | ||
图片预览


文档简介
(共20张PPT)
5 数学广角——鸽巢问题
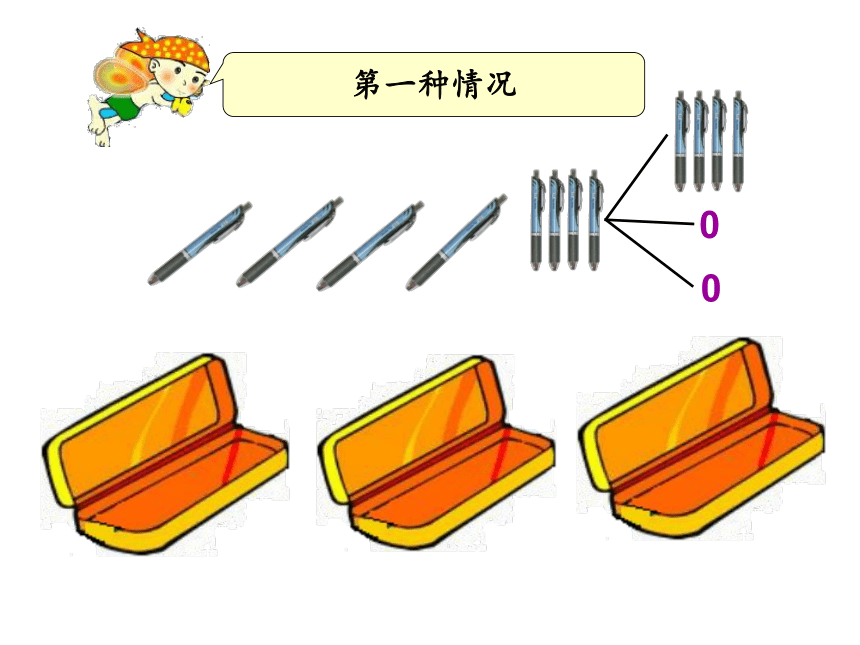
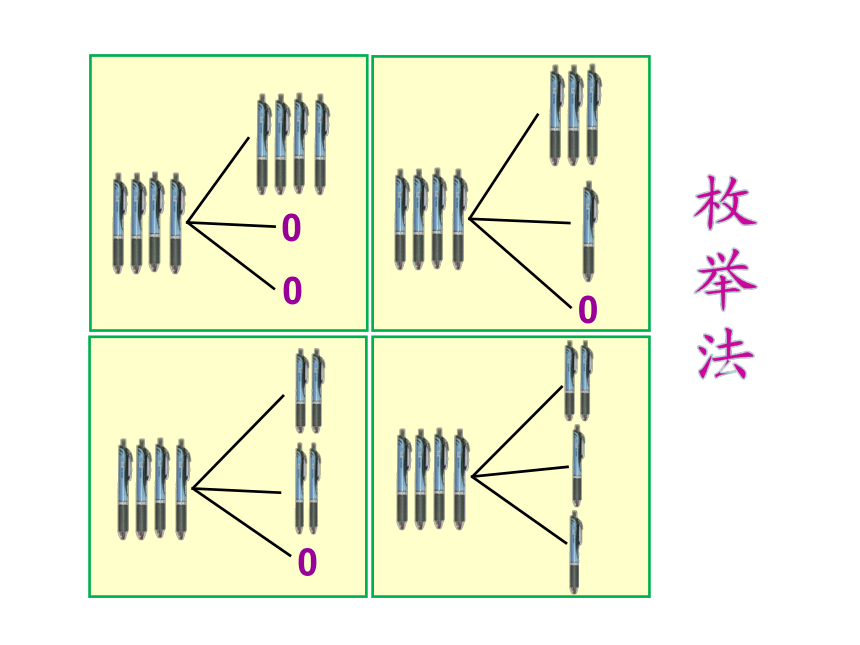
拿出4枝笔和3个文具盒,把这4枝笔放进这3个文具盒中摆一摆,放一放,看有几种情况?
小组合作交流:
第一种情况
0
0
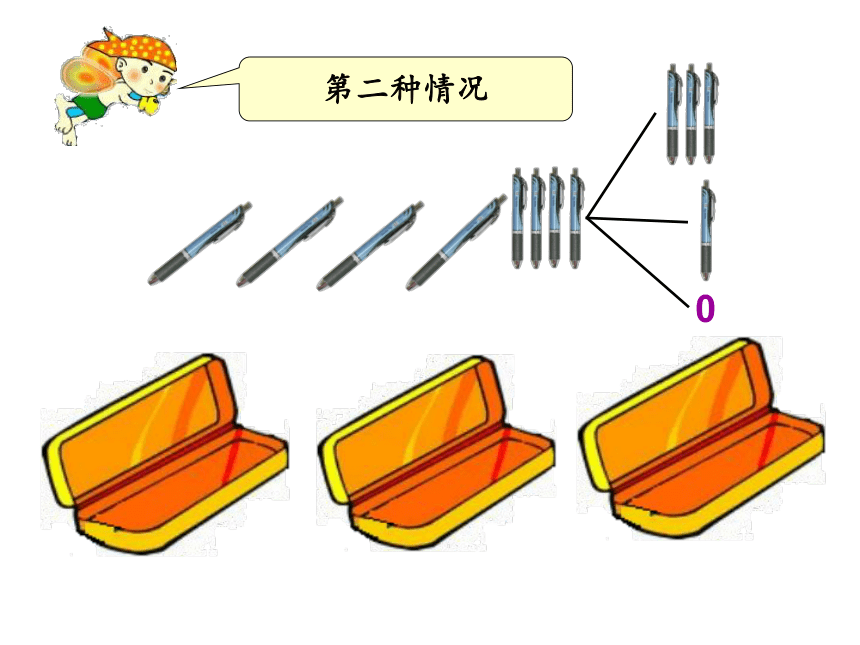
第二种情况
0
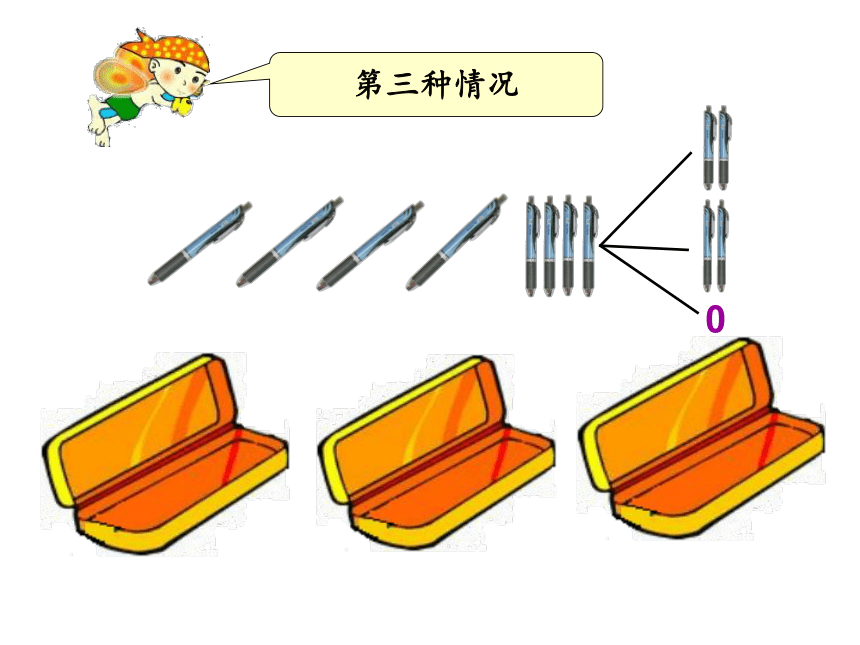
第三种情况
0
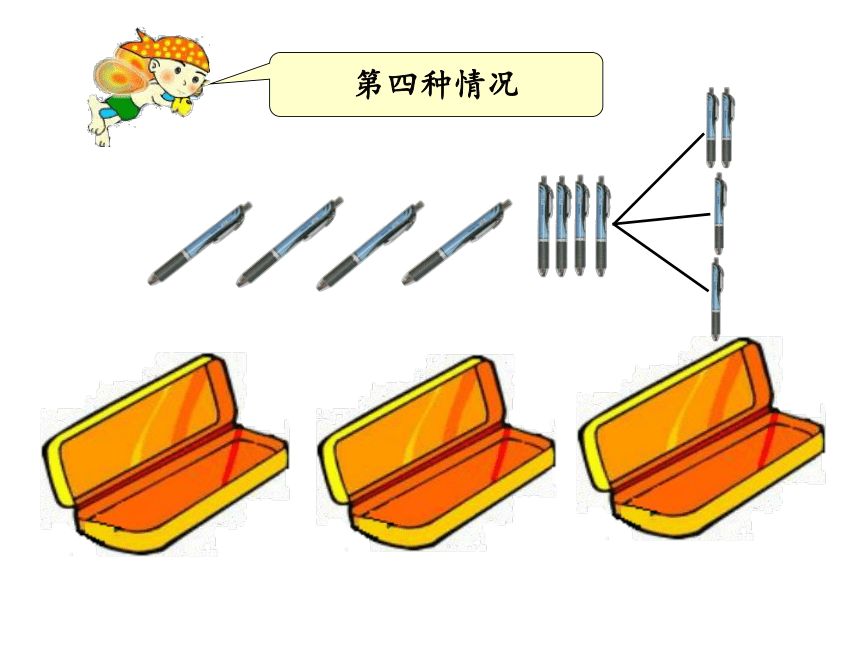
第四种情况
0
0
0
0
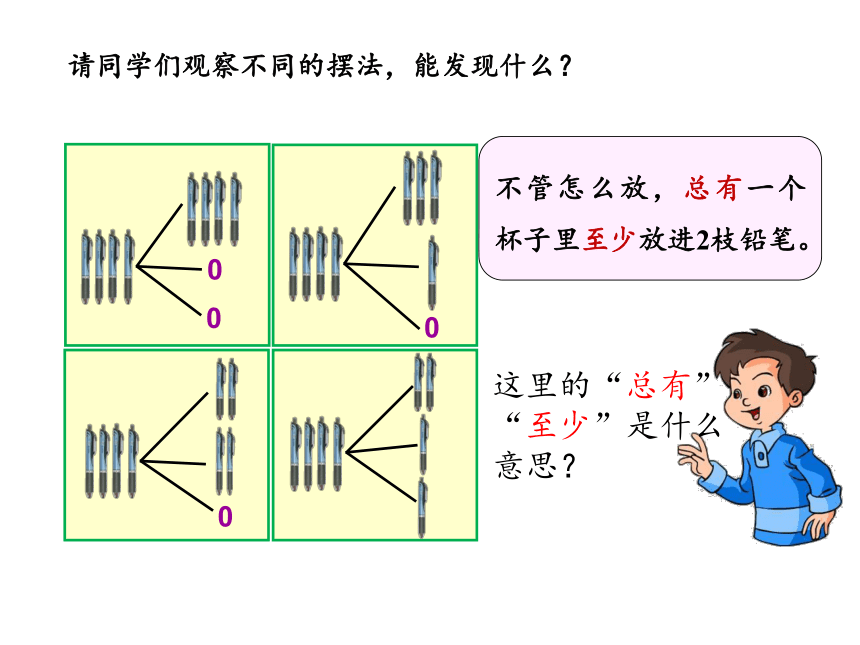
不管怎么放,总有一个杯子里至少放进2枝铅笔。
请同学们观察不同的摆法,能发现什么?
这里的“总有”
“至少”是什么
意思?
0
0
0
0
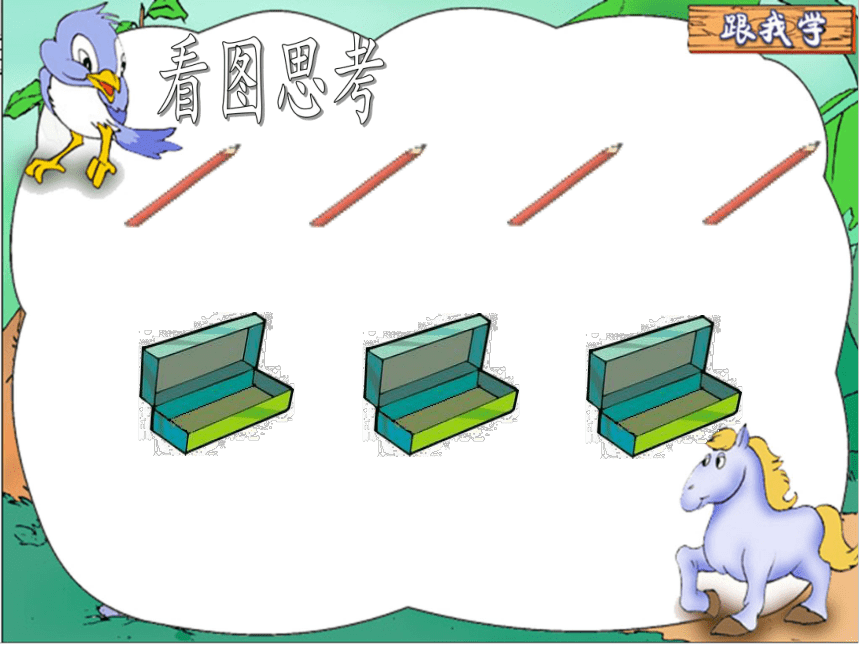
看图思考
可以假设先在每个杯子中分别放入1枝笔,最多可放3枝。剩下的1枝还要放进其中的一个杯子。所以至少有2枝笔放进同一个杯子里。也就是先平均分,然后把剩下的1枝,不管放在哪个杯子里,一定会出现总有一个杯子里至少有2枝铅笔。
看图思考
4÷ 3= 1(只) · · · · · ·1(只)
1+1=2(只)
只要笔的只数比杯子的个数 ,那么不管怎么放,总有一个杯子里,至少有 只笔 。
多1
2
总结结论
那么如果要放的铅笔数比杯子的数量
多3,多4,多5,上述的结论仍然成立吗?
“鸽巢原理”最先是由德国数学家狄里克雷运用于解决数学问题的,所以又称“狄里克雷原理”,现在通常称为“抽屉原理”。 “抽屉原理”在很多领域都得到了广泛的应用。
鸽巢原理
你知道吗?
把7本书放进3个抽屉中,不管怎么放,总有一个抽屉至少放进几本书?为什么?
7÷ 3= 2(本) · · · · · ·1(本)
2+1=3(本)
把7本书平均分成3份,每个抽屉放2本,则还剩1本。如果把剩下的这1本书放进任意1个抽屉中,那么这个抽屉里就有3本书。
只要物体的个数比抽屉个数 ,那么,不管怎么放,总有一个抽屉里,至少有 个物体。
“商+1”
多
总结结论
要把a个物体放进n个抽屉,
如果a ÷n=b · · · · · ·1,
那么一定有一个抽屉至少可以
放入(b+1)个物体。
温馨提示:
在有些问题中,“抽屉”和“物体”不是很明显,就需要我们构造出“抽屉”和“物体”。
解决“抽屉问题”关键是找准哪
是物体,哪是抽屉
解决问题
1、实验小学六(1)班第一小组有13名学生,一定至少有2名学生的生日在同一个月。为什么?
1年有12个月
12个
13名学生
13个物体
试一试吧!
从扑克牌中取出两张王牌,在剩下的52张中任意抽出5张,至少有2张是同花色的。试一试,并说明理由。
4种花色
4个
抽5张牌
5个物体
同学们,通过今天的学习,你有了什么新的收获?
回顾反思
谢 谢
5 数学广角——鸽巢问题
拿出4枝笔和3个文具盒,把这4枝笔放进这3个文具盒中摆一摆,放一放,看有几种情况?
小组合作交流:
第一种情况
0
0
第二种情况
0
第三种情况
0
第四种情况
0
0
0
0
不管怎么放,总有一个杯子里至少放进2枝铅笔。
请同学们观察不同的摆法,能发现什么?
这里的“总有”
“至少”是什么
意思?
0
0
0
0
看图思考
可以假设先在每个杯子中分别放入1枝笔,最多可放3枝。剩下的1枝还要放进其中的一个杯子。所以至少有2枝笔放进同一个杯子里。也就是先平均分,然后把剩下的1枝,不管放在哪个杯子里,一定会出现总有一个杯子里至少有2枝铅笔。
看图思考
4÷ 3= 1(只) · · · · · ·1(只)
1+1=2(只)
只要笔的只数比杯子的个数 ,那么不管怎么放,总有一个杯子里,至少有 只笔 。
多1
2
总结结论
那么如果要放的铅笔数比杯子的数量
多3,多4,多5,上述的结论仍然成立吗?
“鸽巢原理”最先是由德国数学家狄里克雷运用于解决数学问题的,所以又称“狄里克雷原理”,现在通常称为“抽屉原理”。 “抽屉原理”在很多领域都得到了广泛的应用。
鸽巢原理
你知道吗?
把7本书放进3个抽屉中,不管怎么放,总有一个抽屉至少放进几本书?为什么?
7÷ 3= 2(本) · · · · · ·1(本)
2+1=3(本)
把7本书平均分成3份,每个抽屉放2本,则还剩1本。如果把剩下的这1本书放进任意1个抽屉中,那么这个抽屉里就有3本书。
只要物体的个数比抽屉个数 ,那么,不管怎么放,总有一个抽屉里,至少有 个物体。
“商+1”
多
总结结论
要把a个物体放进n个抽屉,
如果a ÷n=b · · · · · ·1,
那么一定有一个抽屉至少可以
放入(b+1)个物体。
温馨提示:
在有些问题中,“抽屉”和“物体”不是很明显,就需要我们构造出“抽屉”和“物体”。
解决“抽屉问题”关键是找准哪
是物体,哪是抽屉
解决问题
1、实验小学六(1)班第一小组有13名学生,一定至少有2名学生的生日在同一个月。为什么?
1年有12个月
12个
13名学生
13个物体
试一试吧!
从扑克牌中取出两张王牌,在剩下的52张中任意抽出5张,至少有2张是同花色的。试一试,并说明理由。
4种花色
4个
抽5张牌
5个物体
同学们,通过今天的学习,你有了什么新的收获?
回顾反思
谢 谢
