4.2 第3课时 线段的性质 课件(共18张PPT)
文档属性
| 名称 | 4.2 第3课时 线段的性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 21:23:44 | ||
图片预览






文档简介
(共18张PPT)
第四章 几何图形初步
4.2 第3课时 线段的性质
随堂演练
课堂小结
例题讲解
知识回顾
获取新知
知识回顾
点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点.
线段中点的定义
A
a
a
M
B
几何语言:
∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:
∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
获取新知
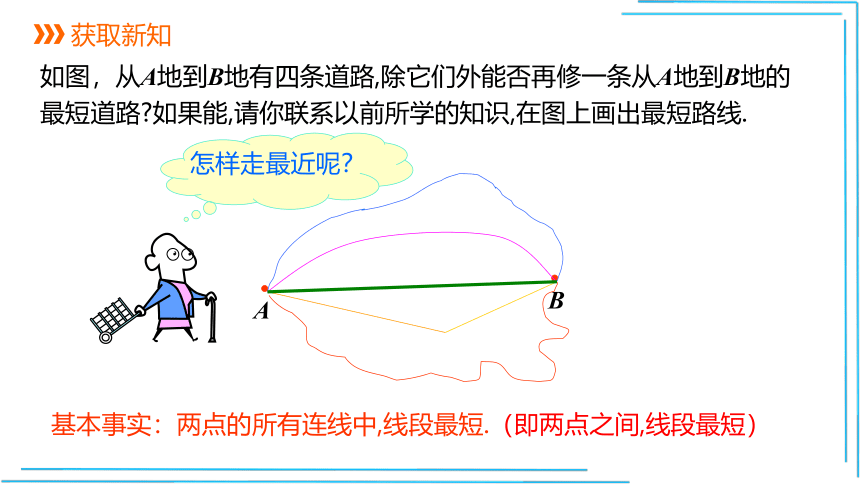
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路 如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
怎样走最近呢?
基本事实:两点的所有连线中,线段最短.
(即两点之间,线段最短)
连接两点间的线段的长度,叫做这两点的距离.
备注:距离不是线段.
线段是一个几何图形;
距离是一个量,它反映的是线段的长短.距离是一个数量且有长度单位.
A
B
例1 直线a表示一条河,在河两侧有两个村庄A和B。要在河边建一个供水站C,使C到两村庄的距离之和最小。请找出C点的位置,并说明理由。
a
A
B
C
例题讲解
点C即为所求. 理由:两点之间,线段最短
在解决选择位置、求最短距离等问题时,通常利用“两点之间,线段最短”.
例2. 把原来弯曲的河道改直,A,B 两地间的河道长度有什么变化?
A,B 两地间的河道长度变短.
例3.如图:AB+AC_____BC,理由是:____________________
启发提问:三角形的任意两边的和与第三边什么关系?
>
两点之间,线段最短
三角形的任意两边之和大于第三边
如图,一只蚂蚁要从正方体的顶点A沿表面爬行到顶点C,怎样爬行路线最短?
C
B
A
C
A
注意:把立体图形转化为平面图形,利用“两点之间,线段最短”找出最短路线
随堂演练
1. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
C
2 如图所示,由M到N有①②③④共4条路线,最
短的路线选①的理由是( )
A.因为它是直线
B.两点确定一条直线
C.两点之间的距离
D.两点之间,线段最短
D
3.下列说法正确的是( )
A.两点之间,直线最短
B.线段MN就是M,N两点间的距离
C.在连接两点的所有线中,最短的连线的长度就是这两点间的距离
D.从武汉到北京,火车行走的路程就是武汉到北京的距离
C
4.下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程.
其中可用基本事实“两点之间,线段最短”来解释的现象有( )
A. ①② B.①③ C.②④ D.③④
D
5.点B在线段AC上,AB=5,BC=3,则A、C 两点的距离是( )
A
A. 8 B.2 C.4 D.无法确定
6.如下图,设A、B、C、D为4个居民小区,现在要在居民小区内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?说明理由。
C
●
●
●
●
B
D
A
●
M
解:
则点M为购物中心的位置。
课堂小结
线段的性质
基本事实
两点间的距离
两点之间,线段最短
两点间的线段的长度
https://www.21cnjy.com/help/help_extract.php
第四章 几何图形初步
4.2 第3课时 线段的性质
随堂演练
课堂小结
例题讲解
知识回顾
获取新知
知识回顾
点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点.
线段中点的定义
A
a
a
M
B
几何语言:
∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:
∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
获取新知
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路 如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
怎样走最近呢?
基本事实:两点的所有连线中,线段最短.
(即两点之间,线段最短)
连接两点间的线段的长度,叫做这两点的距离.
备注:距离不是线段.
线段是一个几何图形;
距离是一个量,它反映的是线段的长短.距离是一个数量且有长度单位.
A
B
例1 直线a表示一条河,在河两侧有两个村庄A和B。要在河边建一个供水站C,使C到两村庄的距离之和最小。请找出C点的位置,并说明理由。
a
A
B
C
例题讲解
点C即为所求. 理由:两点之间,线段最短
在解决选择位置、求最短距离等问题时,通常利用“两点之间,线段最短”.
例2. 把原来弯曲的河道改直,A,B 两地间的河道长度有什么变化?
A,B 两地间的河道长度变短.
例3.如图:AB+AC_____BC,理由是:____________________
启发提问:三角形的任意两边的和与第三边什么关系?
>
两点之间,线段最短
三角形的任意两边之和大于第三边
如图,一只蚂蚁要从正方体的顶点A沿表面爬行到顶点C,怎样爬行路线最短?
C
B
A
C
A
注意:把立体图形转化为平面图形,利用“两点之间,线段最短”找出最短路线
随堂演练
1. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
C
2 如图所示,由M到N有①②③④共4条路线,最
短的路线选①的理由是( )
A.因为它是直线
B.两点确定一条直线
C.两点之间的距离
D.两点之间,线段最短
D
3.下列说法正确的是( )
A.两点之间,直线最短
B.线段MN就是M,N两点间的距离
C.在连接两点的所有线中,最短的连线的长度就是这两点间的距离
D.从武汉到北京,火车行走的路程就是武汉到北京的距离
C
4.下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程.
其中可用基本事实“两点之间,线段最短”来解释的现象有( )
A. ①② B.①③ C.②④ D.③④
D
5.点B在线段AC上,AB=5,BC=3,则A、C 两点的距离是( )
A
A. 8 B.2 C.4 D.无法确定
6.如下图,设A、B、C、D为4个居民小区,现在要在居民小区内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?说明理由。
C
●
●
●
●
B
D
A
●
M
解:
则点M为购物中心的位置。
课堂小结
线段的性质
基本事实
两点间的距离
两点之间,线段最短
两点间的线段的长度
https://www.21cnjy.com/help/help_extract.php
