直线与圆的位置关系

(共24张PPT)
赵 俊 娥
活动一
在纸上画出一个圆，把一根较细的笔看做直线，将笔在纸面上任意移动，观察直线与圆的公共点的个数，并指出直线与圆有几种不同的位置关系。
O
阅读课本上37页内容，并试做：
（1）直线和圆有两个公共点时，叫做直线和圆 ；
（2）直线和圆有唯一公共点时，叫做直线和圆 ；
这时直线叫做圆的 . 唯一的公共点叫做 。
（3）直线和圆没有公共点时，叫做直线和圆
直线与圆有 位置关系。
三种
相交
相切
切线
切点
相离。
试一试
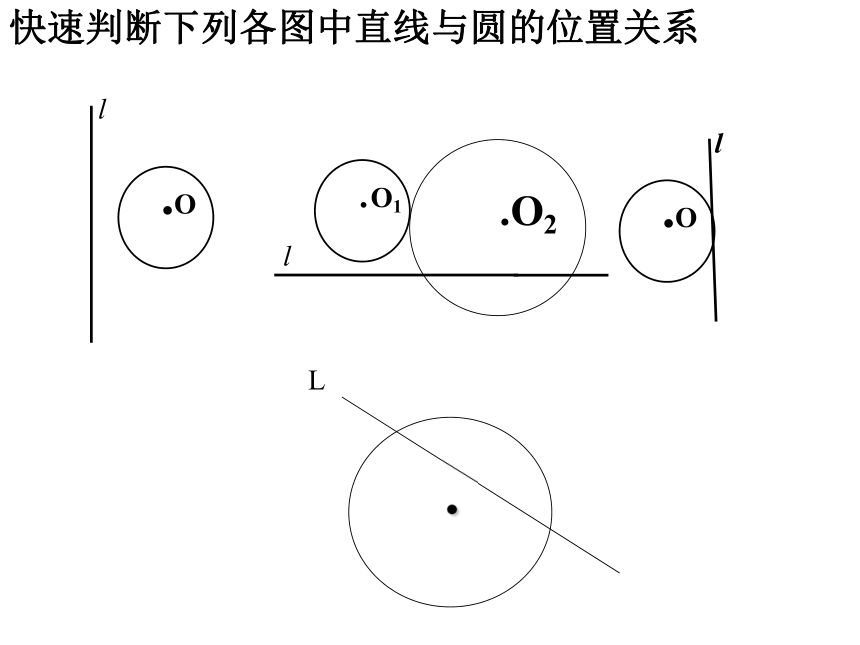
快速判断下列各图中直线与圆的位置关系
.O
l
.O1
.O
l
.O2
l
L
.
直线与圆有第四种关系吗？
即直线与圆是否有第三个交点？
.O
是是非非
１、直线与圆最多有两个公共
点 。…………………（　）
√
.O
是是非非
×
.C
２、若C为⊙O上的一点，则过点C的直线与⊙O相切。… … … …( )
是是非非
3 、若A、B是⊙O外两点， 则直线AB
与⊙O相离。… … … … …( )
×
.A1
.B1
.O
.A
.B
.B2
.A2
是是非非
√
.
C
4、若C为⊙O内一点，则过点C的直线与⊙O相交。（ ）
.
O
新的问题：
能用直线与圆的公共点的个数来判断直线与圆的位置关系。
是否还有其它的方法来判断直线与圆的位置关系？
复习提问
点和圆的位置关系有几种？
（1） 点在圆内
（2） 点在圆上
（3） 点 在圆外
若将点改成直线 ，那么直线与圆的位置关系又如何呢？
dd=r
d>r
1、直线与圆的位置关系，r与d之间的数量关系分别是怎样的？
d
o
r
l
d
o
r
l
o
d
r
l
2、完成书上38页的填表。
（1）直线l 和⊙O相离
d>r
（2）直线l 和⊙O相切
d=r
（3）直线l 和⊙O相交
d3、用圆心到直线的距离和圆半径的数量关系，来揭示圆和直线的位置关系。
总结：
判定直线 与圆的位置关系的方法有____种：
（1）根据定义，由________________
的个数来判断；
（2）根据性质，由_________________ 的关系来判断。
在实际应用中，常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
说说收获
直线与圆的位置关系
直线与圆的
位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
例 在Rt
ABC中，∠ C=90°，AC=3cm, BC= 4cm,
圆心，r为半径的圆与AB有怎样的位置关系？
则以C为
(1）r =2cm, (2) r =2.4cm (3) r =3cm
C
A
B
3
4
分析：
D
3、故应求什么？怎么做？
需比较点C到直线AB的距离与半径r的大小
2、要判断圆与AB的位置关系须比较什么？
C到直线AB的距离
4、要求CD, 应考虑用什么方法？
等面积法
1、什么叫点到直线的距离？
点到直线的垂线段的长度
1、已知圆的直径为13cm，设直线和圆心的距离为d ：
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆　　　, 直线与圆有____个公共点.
3)若AB和⊙O相交,则 .
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
随堂练习
0cm≤
2
1
0
3.直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相交
相切
相离
1、设⊙O的半径为4，点O到直线a的距离为d，
若⊙O与直线a至多只有一个公共点，则d为…（ ）
A、d≤4 B、d＜4 C、d≥4 D、d＝4
2、设⊙p的半径为4cm，直线l上一点A到圆心的
距离为4cm，则直线l与⊙O的位置关系
是……………………………………………（ ）
A、相交 B、相切 C、相离 D、相切或相交
C
D
拓展练习
拓展练习
2、识别直线与圆的位置关系的方法：
（1）一种是根据定义进行识别：
直线L与⊙o没有公共点 直线L与⊙o相离。
直线L与⊙o只有一个公共点 直线L与⊙o相切。
直线L与⊙o有两个公共点 直线L与⊙o相交。
（2）另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别：
d>r 直线L与⊙o相离；
d=r 直线L与⊙o相切；
d1、直线与圆的位置关系3种：相离、相切和相交。
希望大家如这朝阳,
越升越高!越开越艳!
Bye！