三视图
图片预览










文档简介
(共77张PPT)
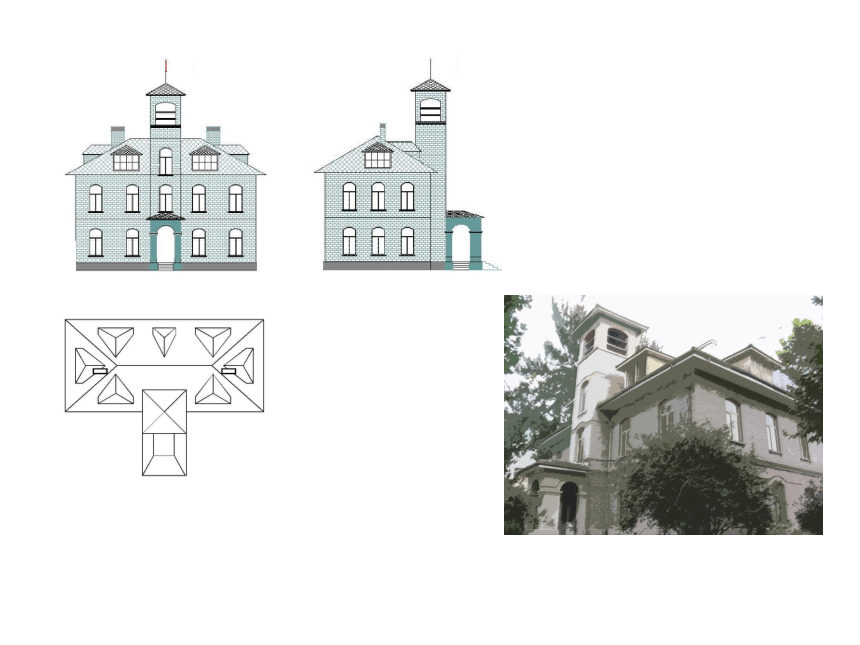
问题二:如果要建造房子,你是工程师, 需要给施工员提供哪几种的图纸?
三视图法:从正面、上面和侧面(左面或右面)三个不同的方向看一个物体,然后描绘三张所看到的图,即视图。
首页
问题一:要很好的描绘这幢房子,需要从哪些方向去看?
新华社8月25日电: 2005年8月18日-25日历时8天的“和平使命-2005”中俄联合军事演习25日下午结束,曹刚川和伊万诺夫在演兵场检阅了两军陆海空军参演部队。 ... 伊万诺夫在俄中军事演习结束后表示,今后两国还将会举行新的联合军事演习,俄中携手团结将成为亚太地区和平与稳定的重要保障。
新闻连接
在本次军演中展出了我国不少先进的武器:
看一看
看一看
看一看
看一看
聪明的同学们,你发现了吗 我们总是从哪几个角度来展示的.
从正面看
从侧面看
从上面看
飞机
模型
在生活中我们应从不同角度,多方面地去看待一件事物,分析一件事情。
数学中我们只从三个不同方向看同一物体,所以,每一个物体都有三视图。
下面我们讨论三视图的问题.
图29.2-2是同一本书的三个不同的视图.
你能说出这三个视图分别是从哪个方向观察这本书时得到的吗?
如图,我们用三个互相垂直的平面(例如墙角处的三面墙壁)作为投影面.
其中正对着我们的叫做正面.
正面下方的叫做水平面,
右边的叫做侧面.
正面
侧面
水平面
主视图
俯视图
左视图
投影面
一个物体(例如一个长方体)在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图(从前面看);
在水平面内得到的由上向下观察物体的视图,叫做俯视图(从上面看)
在侧面内得到由左向右观察物体的视图,叫做左视图(从左面看).
三视图是主视图、俯视图、左视图的
统称。它是从三个方向分别表示物体形状
的一种常用视图。
将三个投影面展开在一个平面内,得到这一物体的一张三视图
主视图
主视图
俯视图
左视图
正面
从上面看
从正面看
从左面看
P116 三视图(1)
高
长
宽
宽
主视图
主视图
俯视图
左视图
正面
P116 三视图(2)
高
长
宽
宽
俯视图
主视图
主视图
左视图
正面
P116 三视图(2)
高
长
宽
宽
俯视图
主视图
主视图
左视图
正面
P116 三视图(2)
高
长
宽
宽
俯视图
主视图
左视图
高
长
宽
宽
俯视图
高对齐
长对齐
宽相等
正方形
正方形
画视图时:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
在实际生活中人们经常遇到各类种物体,这些物体的现状虽然经常各不相同,但是它们一般是由一些基本几何体(柱体、锥体、球等)组合或切割而成的,因此会画、会看基本几何体的视图是非常必要的.
三视图中,主视图与俯视图表示同一物体的长,主视图与左视图表示同一物体的高,左视图与俯视图表示同一物体的宽,因此三个视图的大小是互相联系的,画三视图时,三个视图要放在正确的位置
侧面
水平面
主视图
俯视图
左视图
投影面
主视图
左视图
俯视图
长
长
高
高
宽相等
从上面看
从左面看
从正面看
主视图
左视图
俯视图
3. 在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
例1 画出图所示一些基本几何体的三视图.
分析:画这些基本几何体的三视图时,要注意从三个方面观察它们,具体画法为:
1.确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注意与主视图“长对正”;
圆
柱
主视图
俯视图
左视图
三棱柱
主视图
俯视图
左视图
四棱锥
主视图
俯视图
左视图
球
主视图
俯视图
左视图
下图中物体形状可以看成什么样的几何体
圆锥
从正面,侧面,上面看这个几何体,它的形状是什么样的
正面看: 等腰三角形
侧面看: 等腰三角形
上面看: 圆和一个点
你能画出三视图吗
正视图
侧视图
俯视图
·
圆锥三视图
画出如图4.2.3和图4.2.4所示的正方形和圆柱的三视图。
4.2.3
4.2.4
正视图
左视图
俯视图
4.2.5
解:如图4.2.5,正方体的三视图都是正方形。
首页
正视图
左视图
俯视图
4.2.6
如图4.2.6,圆柱的正视图和左视图都是长方形,俯视图是圆。
首页
画出如图4.2.7所示四棱锥的三视图。
解:四棱锥的三视图如图4.2.8:
正视图
左视图
俯视图
4.2.7
4.2.8
首页
基本几何体的三视图:
(1)正方体的三视图都是正方形。
(2)圆柱的三视图中有两个是长方形,另一个是圆。
(3)圆锥的三视图中有两个是三角形,另一个是圆和一个点。
(4)四棱锥的三视图中有两个是三角形,另一个是矩形和它的对角线。
(5)球体的三视图都是圆形。
例2 画出图所示的支架(一 种小零件)的三视图.
分析:支架的现状:由两个大小不等的长方体构成的组合体,画三视图时要注意这两个长方体的上下、前后位置关系.
解:图是支架的三视图.
主视图
俯视图
左视图
例3 图是一根钢管的直观图,画出它的三视图.
分析:钢管有内外壁,从一定角度看它时,看不见内壁,为全面地反映立体图形的现状,画图时规定:
看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
解:图是钢管的三视图,其中的虚线表示钢管的内壁.
主视图
俯视图
左视图
1. 画出如图所示的三棱柱的三视图(这个三柱上下底面是正三角形).
练 习
三棱柱
主视图
俯视图
左视图
2. 画出半球和圆锥的三视图.
半圆
主视图
俯视图
左视图
圆锥
主视图
俯视图
左视图
·
3. 图中的立体图形可以看成由哪些基本几何体经过怎样的变化得到的?
主视图
俯视图
左视图
(4)画出下列几何体的三种试图:
主视图
俯视图
左视图
长方体
圆台
画出下列基本几何体的三视图练习一:
六棱锥
长方体
长方体
正视图
侧视图
俯视图
圆台
圆台
正视图
侧视图
俯视图
六棱锥
小结:若相邻的两平面的相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出。
六棱锥的三视图
画出下面几何体的三视图。
简单组合体的三视图
正视图
侧视图
俯视图
简单组合体的三视图
注意:不可见的轮廓线,用虚线画出。
正视图
侧视图
俯视图
简单组合体的三视图
你能想象出下面各几何体的主视图,左视图,俯视图吗?
我思我进步
1
实物的三视图
正三棱柱 四棱柱
你能画出它们主视图,左视图,俯视图吗?
空间想象力
2
三视图
主视图
宽
俯视图
左视图
老师提示:
在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画三视图要认真准确,特别是宽相等.
宽
主视图
左视图
俯视图
空间想象力
3
“做一做”
已知俯视图,画出它的主视图,左视图.
下图是底面为等腰直角三角形和等腰梯形的
三棱柱,四棱柱的俯视图,尝试画出它的主视图
和左视图,并与同伴交流.
俯视图(1)
俯视图(2)
俯视图(3)
俯视图(4)
主视图
左视图
主视图
左视图
俯视图(1)
俯视图(2)
驶向胜利彼岸
空间想象力
1
主视图
左视图
俯视图(3)
主视图
左视图
俯视图(4)
驶向胜利彼岸
空间想象力
1
理一理:
1、从正面看到的图形叫做主视图,从上面看到的图形叫做俯视图,从左面看到的图形叫做左视图。
2、画三视图必须遵循的法则:“长对齐,高平齐,宽相等”
3、基本几何体的三视图:
(1)正方体的三视图都是正方形。
(2)圆柱的三视图中有两个是长方形,另一个是圆。
(3)圆锥的三视图中有两个是三角形,另一个是圆。
(4)棱锥的三视图中有两个是三角形,另一个是正方形。
(5)球体的三视图都是圆形。
1、画出下列立体图形的三视图。
2、指出左面三个平面图形是右面这个物体的三视图中
的哪个视图。
(
(
(
正视图)
俯视图)
左视图)
练一练
请画出如图所示的三视图
(A)
(1)
(2)
平面图形
学到了什么?
平面图
看到了什么画什么
从正
面看
从左
面看
从上
面看
实物图
立体图
平面图
平面图
三视图
主视图
左视图
俯视图
想一想?
A
C
B
D
下面三视图是表示哪个几何体?
侧视图
正视图
俯视图
A
B
思考:下图中的三视图表示哪个几何体?
俯视图
左视图
正视图
A
B
C
( )
( )
( )
B
C
B
俯视图
左视图
正视图
A
B
C
( )
( )
( )
A
A
B
考考你
【探究】
1、如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
探究
你能摆出这个几何体吗?
试画出这个几何体的正视图与侧视图。
正视图:
侧视图:
1
1
2
2
1
1
2
2
正视图:
侧视图:
思考方法
先根据俯视图确定正视图有 列,
3
再根据数字确定每列的方块有 个,
不用摆出这个几何体,你能画出这个几何体的正视图与左视图吗?
正视图有 列,
第一列的方块有 个,
1
第二列的方块有 个,
2
第三列的方块有 个,
1
侧视图有 列,
2
第一列的方块有 个,
2
第二列的方块有 个,
2
【反思】
2、你能由三视图得到该几何体吗?
3、你会由“给出数字的俯视图”画出几何体的正视图、侧视图吗?
1、你能画出一个几何体的三视图吗?
动手设计
请画出下面立体图形的三视图。
俯视方向
注意:根据“长对正,高平齐,宽相等” 画
三视图必须遵循的法则作图。
画好后,请你自己参照课本65页的图3—21给自己画的
图打分,并把画得不够好的地方修改过来,加油!
辨一辨,说一说:
1、一个几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。请你举一些例子加以说明。
提示:例如正方体的主视图是一个张方形,但主视图是正方形的几何体就有很多,如四棱柱,长方体,圆柱等。
三视图
三视图
主视图——从正面看到的图
左视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
挑战“自我”,提高画三视图的能力.
小结 反馈
位置:
投影规律
主视图反映了物体上下、左右的位置关系,即反映了物体的 高度和长度;
俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度;
左视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度。
由此可得出三视图之间的投影规律为:
主、俯视图——长对正;主、左视图——高平齐;俯、左视图——宽相等。
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
想一想:
题西林壁 苏轼
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
诗中说明了怎样的一个数学道理?
横看成岭侧成峰,
远近高低各不同.
不识庐山真面目,
只缘身在此山中.
题西林壁
苏轼
2、会画简单立体图形的三视图.
1、三视图的概念;
谈谈收获
问题二:如果要建造房子,你是工程师, 需要给施工员提供哪几种的图纸?
三视图法:从正面、上面和侧面(左面或右面)三个不同的方向看一个物体,然后描绘三张所看到的图,即视图。
首页
问题一:要很好的描绘这幢房子,需要从哪些方向去看?
新华社8月25日电: 2005年8月18日-25日历时8天的“和平使命-2005”中俄联合军事演习25日下午结束,曹刚川和伊万诺夫在演兵场检阅了两军陆海空军参演部队。 ... 伊万诺夫在俄中军事演习结束后表示,今后两国还将会举行新的联合军事演习,俄中携手团结将成为亚太地区和平与稳定的重要保障。
新闻连接
在本次军演中展出了我国不少先进的武器:
看一看
看一看
看一看
看一看
聪明的同学们,你发现了吗 我们总是从哪几个角度来展示的.
从正面看
从侧面看
从上面看
飞机
模型
在生活中我们应从不同角度,多方面地去看待一件事物,分析一件事情。
数学中我们只从三个不同方向看同一物体,所以,每一个物体都有三视图。
下面我们讨论三视图的问题.
图29.2-2是同一本书的三个不同的视图.
你能说出这三个视图分别是从哪个方向观察这本书时得到的吗?
如图,我们用三个互相垂直的平面(例如墙角处的三面墙壁)作为投影面.
其中正对着我们的叫做正面.
正面下方的叫做水平面,
右边的叫做侧面.
正面
侧面
水平面
主视图
俯视图
左视图
投影面
一个物体(例如一个长方体)在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图(从前面看);
在水平面内得到的由上向下观察物体的视图,叫做俯视图(从上面看)
在侧面内得到由左向右观察物体的视图,叫做左视图(从左面看).
三视图是主视图、俯视图、左视图的
统称。它是从三个方向分别表示物体形状
的一种常用视图。
将三个投影面展开在一个平面内,得到这一物体的一张三视图
主视图
主视图
俯视图
左视图
正面
从上面看
从正面看
从左面看
P116 三视图(1)
高
长
宽
宽
主视图
主视图
俯视图
左视图
正面
P116 三视图(2)
高
长
宽
宽
俯视图
主视图
主视图
左视图
正面
P116 三视图(2)
高
长
宽
宽
俯视图
主视图
主视图
左视图
正面
P116 三视图(2)
高
长
宽
宽
俯视图
主视图
左视图
高
长
宽
宽
俯视图
高对齐
长对齐
宽相等
正方形
正方形
画视图时:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
在实际生活中人们经常遇到各类种物体,这些物体的现状虽然经常各不相同,但是它们一般是由一些基本几何体(柱体、锥体、球等)组合或切割而成的,因此会画、会看基本几何体的视图是非常必要的.
三视图中,主视图与俯视图表示同一物体的长,主视图与左视图表示同一物体的高,左视图与俯视图表示同一物体的宽,因此三个视图的大小是互相联系的,画三视图时,三个视图要放在正确的位置
侧面
水平面
主视图
俯视图
左视图
投影面
主视图
左视图
俯视图
长
长
高
高
宽相等
从上面看
从左面看
从正面看
主视图
左视图
俯视图
3. 在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
例1 画出图所示一些基本几何体的三视图.
分析:画这些基本几何体的三视图时,要注意从三个方面观察它们,具体画法为:
1.确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注意与主视图“长对正”;
圆
柱
主视图
俯视图
左视图
三棱柱
主视图
俯视图
左视图
四棱锥
主视图
俯视图
左视图
球
主视图
俯视图
左视图
下图中物体形状可以看成什么样的几何体
圆锥
从正面,侧面,上面看这个几何体,它的形状是什么样的
正面看: 等腰三角形
侧面看: 等腰三角形
上面看: 圆和一个点
你能画出三视图吗
正视图
侧视图
俯视图
·
圆锥三视图
画出如图4.2.3和图4.2.4所示的正方形和圆柱的三视图。
4.2.3
4.2.4
正视图
左视图
俯视图
4.2.5
解:如图4.2.5,正方体的三视图都是正方形。
首页
正视图
左视图
俯视图
4.2.6
如图4.2.6,圆柱的正视图和左视图都是长方形,俯视图是圆。
首页
画出如图4.2.7所示四棱锥的三视图。
解:四棱锥的三视图如图4.2.8:
正视图
左视图
俯视图
4.2.7
4.2.8
首页
基本几何体的三视图:
(1)正方体的三视图都是正方形。
(2)圆柱的三视图中有两个是长方形,另一个是圆。
(3)圆锥的三视图中有两个是三角形,另一个是圆和一个点。
(4)四棱锥的三视图中有两个是三角形,另一个是矩形和它的对角线。
(5)球体的三视图都是圆形。
例2 画出图所示的支架(一 种小零件)的三视图.
分析:支架的现状:由两个大小不等的长方体构成的组合体,画三视图时要注意这两个长方体的上下、前后位置关系.
解:图是支架的三视图.
主视图
俯视图
左视图
例3 图是一根钢管的直观图,画出它的三视图.
分析:钢管有内外壁,从一定角度看它时,看不见内壁,为全面地反映立体图形的现状,画图时规定:
看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
解:图是钢管的三视图,其中的虚线表示钢管的内壁.
主视图
俯视图
左视图
1. 画出如图所示的三棱柱的三视图(这个三柱上下底面是正三角形).
练 习
三棱柱
主视图
俯视图
左视图
2. 画出半球和圆锥的三视图.
半圆
主视图
俯视图
左视图
圆锥
主视图
俯视图
左视图
·
3. 图中的立体图形可以看成由哪些基本几何体经过怎样的变化得到的?
主视图
俯视图
左视图
(4)画出下列几何体的三种试图:
主视图
俯视图
左视图
长方体
圆台
画出下列基本几何体的三视图练习一:
六棱锥
长方体
长方体
正视图
侧视图
俯视图
圆台
圆台
正视图
侧视图
俯视图
六棱锥
小结:若相邻的两平面的相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出。
六棱锥的三视图
画出下面几何体的三视图。
简单组合体的三视图
正视图
侧视图
俯视图
简单组合体的三视图
注意:不可见的轮廓线,用虚线画出。
正视图
侧视图
俯视图
简单组合体的三视图
你能想象出下面各几何体的主视图,左视图,俯视图吗?
我思我进步
1
实物的三视图
正三棱柱 四棱柱
你能画出它们主视图,左视图,俯视图吗?
空间想象力
2
三视图
主视图
宽
俯视图
左视图
老师提示:
在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画三视图要认真准确,特别是宽相等.
宽
主视图
左视图
俯视图
空间想象力
3
“做一做”
已知俯视图,画出它的主视图,左视图.
下图是底面为等腰直角三角形和等腰梯形的
三棱柱,四棱柱的俯视图,尝试画出它的主视图
和左视图,并与同伴交流.
俯视图(1)
俯视图(2)
俯视图(3)
俯视图(4)
主视图
左视图
主视图
左视图
俯视图(1)
俯视图(2)
驶向胜利彼岸
空间想象力
1
主视图
左视图
俯视图(3)
主视图
左视图
俯视图(4)
驶向胜利彼岸
空间想象力
1
理一理:
1、从正面看到的图形叫做主视图,从上面看到的图形叫做俯视图,从左面看到的图形叫做左视图。
2、画三视图必须遵循的法则:“长对齐,高平齐,宽相等”
3、基本几何体的三视图:
(1)正方体的三视图都是正方形。
(2)圆柱的三视图中有两个是长方形,另一个是圆。
(3)圆锥的三视图中有两个是三角形,另一个是圆。
(4)棱锥的三视图中有两个是三角形,另一个是正方形。
(5)球体的三视图都是圆形。
1、画出下列立体图形的三视图。
2、指出左面三个平面图形是右面这个物体的三视图中
的哪个视图。
(
(
(
正视图)
俯视图)
左视图)
练一练
请画出如图所示的三视图
(A)
(1)
(2)
平面图形
学到了什么?
平面图
看到了什么画什么
从正
面看
从左
面看
从上
面看
实物图
立体图
平面图
平面图
三视图
主视图
左视图
俯视图
想一想?
A
C
B
D
下面三视图是表示哪个几何体?
侧视图
正视图
俯视图
A
B
思考:下图中的三视图表示哪个几何体?
俯视图
左视图
正视图
A
B
C
( )
( )
( )
B
C
B
俯视图
左视图
正视图
A
B
C
( )
( )
( )
A
A
B
考考你
【探究】
1、如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
探究
你能摆出这个几何体吗?
试画出这个几何体的正视图与侧视图。
正视图:
侧视图:
1
1
2
2
1
1
2
2
正视图:
侧视图:
思考方法
先根据俯视图确定正视图有 列,
3
再根据数字确定每列的方块有 个,
不用摆出这个几何体,你能画出这个几何体的正视图与左视图吗?
正视图有 列,
第一列的方块有 个,
1
第二列的方块有 个,
2
第三列的方块有 个,
1
侧视图有 列,
2
第一列的方块有 个,
2
第二列的方块有 个,
2
【反思】
2、你能由三视图得到该几何体吗?
3、你会由“给出数字的俯视图”画出几何体的正视图、侧视图吗?
1、你能画出一个几何体的三视图吗?
动手设计
请画出下面立体图形的三视图。
俯视方向
注意:根据“长对正,高平齐,宽相等” 画
三视图必须遵循的法则作图。
画好后,请你自己参照课本65页的图3—21给自己画的
图打分,并把画得不够好的地方修改过来,加油!
辨一辨,说一说:
1、一个几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。请你举一些例子加以说明。
提示:例如正方体的主视图是一个张方形,但主视图是正方形的几何体就有很多,如四棱柱,长方体,圆柱等。
三视图
三视图
主视图——从正面看到的图
左视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
挑战“自我”,提高画三视图的能力.
小结 反馈
位置:
投影规律
主视图反映了物体上下、左右的位置关系,即反映了物体的 高度和长度;
俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度;
左视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度。
由此可得出三视图之间的投影规律为:
主、俯视图——长对正;主、左视图——高平齐;俯、左视图——宽相等。
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
想一想:
题西林壁 苏轼
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
诗中说明了怎样的一个数学道理?
横看成岭侧成峰,
远近高低各不同.
不识庐山真面目,
只缘身在此山中.
题西林壁
苏轼
2、会画简单立体图形的三视图.
1、三视图的概念;
谈谈收获
