2021-2022学年华东师大版八年级数学上册12.3.1 平方差公式 同步测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册12.3.1 平方差公式 同步测试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 44.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 07:23:45 | ||
图片预览



文档简介
12.3.1 平方差公式同步测试卷 2021-2022学年华东师大版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共11小题,共33分)
平方差公式(a+b)(a-b)=a2-b2中的a,b( )
A. 是数或单个字母 B. 是单项式
C. 是多项式 D. 是单项式或多项式
下列各式中,不能用平方差公式计算的是( )
A. B.
C. D.
下列式子中,能和-5y用平方差公式进行计算的是( )
A. B. C. D.
为了运用平方差公式计算(x+2y-1)(x-2y+1),下列变形正确的是( )
A. B.
C. D.
下列运算正确的是( )
A.
B.
C.
D.
若(2x+3y)(mx-ny)=9y2-4x2,则( )
A. , B. ,
C. , D. ,
若x,y满足|x+y+5|+(x-y-9)2=0,则x2-y2的值为( )
A. B. C. D.
如图①,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下部分沿虚线剪开拼成一个梯形(如图②),利用这两个图形的面积,可以验证的公式是()
A. B.
C. D.
如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )
A. B. C. D.
计算20.82-21.8×19.8的结果是( )
A. B. C. D.
数348﹣1能被30以内的两位整数整除的是()
A. , B. , C. , D. ,
二、填空题(本大题共3小题,共9分)
填空:
(1)59.860.2=( - )( + )= - = ;
(2)1007993=( + )( - )= - = .
(1)如果(2a+2b+1)(2a+2b-1)=3,那么a+b的值为 .
(2)若(m+n-1)(m+1+n)=80,则m+n= .
(3)若(++1)(+-1)-3=0,则+= .
计算:______ .
三、解答题(本大题共6小题,共58分)
已知a-b=2,b-c=2,a+c=14,求a2-b2的值.
已知2a2+3a-6=0,求式子3a(2a+1)-(2a+1)(2a-1)的值.
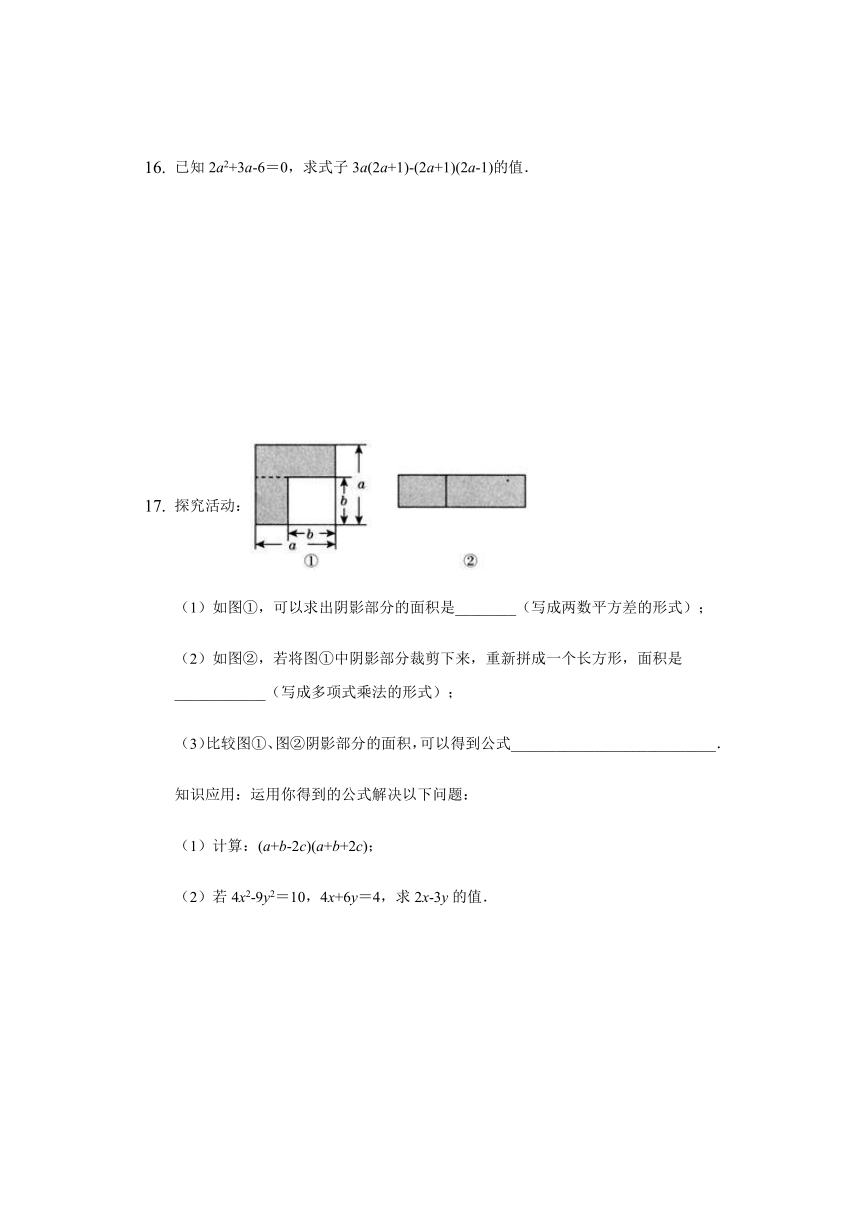
探究活动:
(1)如图①,可以求出阴影部分的面积是________(写成两数平方差的形式);
(2)如图②,若将图①中阴影部分裁剪下来,重新拼成一个长方形,面积是____________(写成多项式乘法的形式);
(3)比较图①、图②阴影部分的面积,可以得到公式___________________________.
知识应用:运用你得到的公式解决以下问题:
(1)计算:(a+b-2c)(a+b+2c);
(2)若4x2-9y2=10,4x+6y=4,求2x-3y的值.
(1)观察下列各式的规律:
( a-b)(a+b)=a2-b2;
( a-b)(a2+ab+b2)=a3-b3;
( a-b)(a3+a2b+ab2+b3)=a4-b4;
…
可得到(a-b)(a2020+a2019b+…+ab2019+b2020)=________.
(2)猜想:(a-b)(an-1+an-2b+…+abn-2+bn-1)=________(其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:29-28+27-…+23-22+2.
如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“奇巧数”,如12=-,20=-,28=-,,因此12,20,28这三个数都是奇巧数.
(1)52,72都是奇巧数吗 为什么
(2)设两个连续偶数为2n,2n+2(其中n为正整数),由这两个连续偶数构造的奇巧数是8的倍数吗 为什么
(3)研究发现:任意两个连续“奇巧数”之差是同一个数,请给出验证.
先观察下面的解题过程,然后解答问题:
化简:(2+1)(+1)(+1).
解:原式=(2-1)(2+1)(+1)(+1)
=(-1)(+1)(+1)
=(-1)(+1)
=-1.
问题:
(1)化简:(2+1)(+1)(+1)(+1)(+1);
(2)求(3+1)(+1)(+1)(+1)(+1)-(n可以写成的形式,m,n均为正整数)的值.
参考答案
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】(1)60 0.2 60 0.2 3600 0.04 3599.96
(2)1000 7 1000 7 999951
13.【答案】1 9 2
14.【答案】3160
15.【答案】解:∵b-c=2,a+c=14,
∴a+b=b-c+a+c=16,
∴a2-b2=(a+b)(a-b)=16×2=32.
16.【答案】解:∵2a2+3a-6=0,即2a2+3a=6,
∴原式=6a2+3a-4a2+1
=2a2+3a+1
=6+1
=7.
17.【答案】解:(1);
(2)(a+b)(a-b);
(3);
知识应用:
(1)原式=[(a+b)-2c][(a+b)+2c]
=
=;
(2)∵,
∴(2x+3y)(2x-3y)=10,2x+3y=2,
∴2x-3y=5.
18.【答案】解:(1)a2021-b2021
(2)由(1)的规律可得:原式=an-bn,
故答案为:an-bn;
(3)
19.【答案】解:(1)52=-,68=-,76=-,
52是奇巧数,72不是奇巧数.
(2)-=(2n+2+2n)(2n+2-2n)=4(2n+1),
这两个连续偶数构造的奇巧数不是8的倍数.
(3)证明:[-]-[-]=(2n+2+2n)(2n+2-2n)-(2n+4+2n+2)(2n+4-2n-2)=4(2n+1)-4(2n+3)=8n+4-8n-12=-8.
任意两个连续“奇巧数”之差是同一个数.
20.【答案】解:(1)原式=(2-1)(2+1)(+1)(+1)(+1)(+1)
=(-1)(+1)(+1)(+1)(+1)
=(-1)(+1)
=-1.
(2)原式= (3-1)(3+1)(+1)(+1)(+1)(+1)-
=(-1)-
=--
=-.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共11小题,共33分)
平方差公式(a+b)(a-b)=a2-b2中的a,b( )
A. 是数或单个字母 B. 是单项式
C. 是多项式 D. 是单项式或多项式
下列各式中,不能用平方差公式计算的是( )
A. B.
C. D.
下列式子中,能和-5y用平方差公式进行计算的是( )
A. B. C. D.
为了运用平方差公式计算(x+2y-1)(x-2y+1),下列变形正确的是( )
A. B.
C. D.
下列运算正确的是( )
A.
B.
C.
D.
若(2x+3y)(mx-ny)=9y2-4x2,则( )
A. , B. ,
C. , D. ,
若x,y满足|x+y+5|+(x-y-9)2=0,则x2-y2的值为( )
A. B. C. D.
如图①,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下部分沿虚线剪开拼成一个梯形(如图②),利用这两个图形的面积,可以验证的公式是()
A. B.
C. D.
如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )
A. B. C. D.
计算20.82-21.8×19.8的结果是( )
A. B. C. D.
数348﹣1能被30以内的两位整数整除的是()
A. , B. , C. , D. ,
二、填空题(本大题共3小题,共9分)
填空:
(1)59.860.2=( - )( + )= - = ;
(2)1007993=( + )( - )= - = .
(1)如果(2a+2b+1)(2a+2b-1)=3,那么a+b的值为 .
(2)若(m+n-1)(m+1+n)=80,则m+n= .
(3)若(++1)(+-1)-3=0,则+= .
计算:______ .
三、解答题(本大题共6小题,共58分)
已知a-b=2,b-c=2,a+c=14,求a2-b2的值.
已知2a2+3a-6=0,求式子3a(2a+1)-(2a+1)(2a-1)的值.
探究活动:
(1)如图①,可以求出阴影部分的面积是________(写成两数平方差的形式);
(2)如图②,若将图①中阴影部分裁剪下来,重新拼成一个长方形,面积是____________(写成多项式乘法的形式);
(3)比较图①、图②阴影部分的面积,可以得到公式___________________________.
知识应用:运用你得到的公式解决以下问题:
(1)计算:(a+b-2c)(a+b+2c);
(2)若4x2-9y2=10,4x+6y=4,求2x-3y的值.
(1)观察下列各式的规律:
( a-b)(a+b)=a2-b2;
( a-b)(a2+ab+b2)=a3-b3;
( a-b)(a3+a2b+ab2+b3)=a4-b4;
…
可得到(a-b)(a2020+a2019b+…+ab2019+b2020)=________.
(2)猜想:(a-b)(an-1+an-2b+…+abn-2+bn-1)=________(其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:29-28+27-…+23-22+2.
如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“奇巧数”,如12=-,20=-,28=-,,因此12,20,28这三个数都是奇巧数.
(1)52,72都是奇巧数吗 为什么
(2)设两个连续偶数为2n,2n+2(其中n为正整数),由这两个连续偶数构造的奇巧数是8的倍数吗 为什么
(3)研究发现:任意两个连续“奇巧数”之差是同一个数,请给出验证.
先观察下面的解题过程,然后解答问题:
化简:(2+1)(+1)(+1).
解:原式=(2-1)(2+1)(+1)(+1)
=(-1)(+1)(+1)
=(-1)(+1)
=-1.
问题:
(1)化简:(2+1)(+1)(+1)(+1)(+1);
(2)求(3+1)(+1)(+1)(+1)(+1)-(n可以写成的形式,m,n均为正整数)的值.
参考答案
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】(1)60 0.2 60 0.2 3600 0.04 3599.96
(2)1000 7 1000 7 999951
13.【答案】1 9 2
14.【答案】3160
15.【答案】解:∵b-c=2,a+c=14,
∴a+b=b-c+a+c=16,
∴a2-b2=(a+b)(a-b)=16×2=32.
16.【答案】解:∵2a2+3a-6=0,即2a2+3a=6,
∴原式=6a2+3a-4a2+1
=2a2+3a+1
=6+1
=7.
17.【答案】解:(1);
(2)(a+b)(a-b);
(3);
知识应用:
(1)原式=[(a+b)-2c][(a+b)+2c]
=
=;
(2)∵,
∴(2x+3y)(2x-3y)=10,2x+3y=2,
∴2x-3y=5.
18.【答案】解:(1)a2021-b2021
(2)由(1)的规律可得:原式=an-bn,
故答案为:an-bn;
(3)
19.【答案】解:(1)52=-,68=-,76=-,
52是奇巧数,72不是奇巧数.
(2)-=(2n+2+2n)(2n+2-2n)=4(2n+1),
这两个连续偶数构造的奇巧数不是8的倍数.
(3)证明:[-]-[-]=(2n+2+2n)(2n+2-2n)-(2n+4+2n+2)(2n+4-2n-2)=4(2n+1)-4(2n+3)=8n+4-8n-12=-8.
任意两个连续“奇巧数”之差是同一个数.
20.【答案】解:(1)原式=(2-1)(2+1)(+1)(+1)(+1)(+1)
=(-1)(+1)(+1)(+1)(+1)
=(-1)(+1)
=-1.
(2)原式= (3-1)(3+1)(+1)(+1)(+1)(+1)-
=(-1)-
=--
=-.
第2页,共2页
