2021-2022学年人教版八年级数学上册14.2乘法公式同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册14.2乘法公式同步练习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 179.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 07:26:19 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学上册《14.2乘法公式》同步练习题(附答案)
1.如图,由4个全等的小长方形与1个小正方形密铺成正方形图案,该图案的面积为49,小正方形的面积为4,若分别用x,y(x>y)表示小长方形的长和宽,则下列关系式中不正确的是( )
A.x2+2xy+y2=49 B.x2﹣2xy+y2=4
C.x2+y2=25 D.x2﹣y2=14
2.下列各式中不能用平方差公式计算的是( )
A.(x+y)(﹣x+y) B.(﹣x+y)(﹣x﹣y)
C.(﹣x﹣y)(x﹣y) D.(x﹣y)(﹣x+y)
3.下列运算正确的是( )
A.(﹣2b3)2=﹣4b6 B.(a﹣b)2=a2﹣b2
C.2a2+a2=3a2 D.2a6÷2a2=a3
4.从前,古希腊一位庄园主把一块边长为a米(a≥6)的正方形土地租给租户王老汉,第二年,他对王老汉说:“我把这块地的一边增加6米,相邻的另边减少6米,变成矩形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得王老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
5.当n为正整数时,代数式(2n+1)2﹣(2n﹣1)2一定是下面哪个数的倍数( )
A.3 B.5 C.7 D.8
6.若x+y=6,x2+y2=20,求x﹣y的值是( )
A.2 B.﹣2 C.4 D.±2
7.关于﹣a﹣b进行的变形或运算:①﹣a﹣b=﹣(a+b);②(﹣a﹣b)2=(a+b)2;③|﹣a﹣b|=a﹣b;④(﹣a﹣b)3=﹣(a﹣b)3.其中不正确的是( )
A.①② B.③④ C.①③ D.②④
8.利用乘法公式判断,下列等式何者成立?( )
A.2482+248×52+522=3002
B.2482﹣248×48﹣482=2002
C.2482+2×248×52+522=3002
D.2482﹣2×248×48﹣482=2002
9.从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加6米,相邻的另一边减少6米,变成矩形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
10.计算(a+b﹣3)(a+b+3)的结果是( )
A.a2+b2﹣9 B.a2﹣b2+6b﹣9
C.a2+2ab+b2﹣9 D.a2﹣b2﹣6b+9
11.我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”
根据”杨辉三角”请计算(a+b)8的展开式中从左起第四项的系数为( )
A.84 B.56 C.35 D.28
12.现有甲、乙、丙三种不同的矩形纸片(边长如图).
(1)取甲、乙纸片各1块,其面积和为 ;
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲纸片1块,再取乙纸片4块,还需取丙纸片 块.
13.若x、y满足,则代数式x2﹣4y2的值为 .
14.若a=b+2,则代数式a2﹣2ab+b2的值为 .
15.设M=x+y,N=x﹣y,P=xy.若M=1,N=2,则P= .
16.若a+b=5,a﹣b=3,则a2﹣b2= .
17.若m﹣=3,则m2+= .
18.杨辉三角,又称贾宪三角,是二项式系数在三角形中的一种几何排列,如图,观察下面的杨辉三角:
按照前面的规律,则(a+b)5= .
19.观察下列各式的规律:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
…
可得到(a﹣b)(a2022+a2021b+…+ab2021+b2022)= .
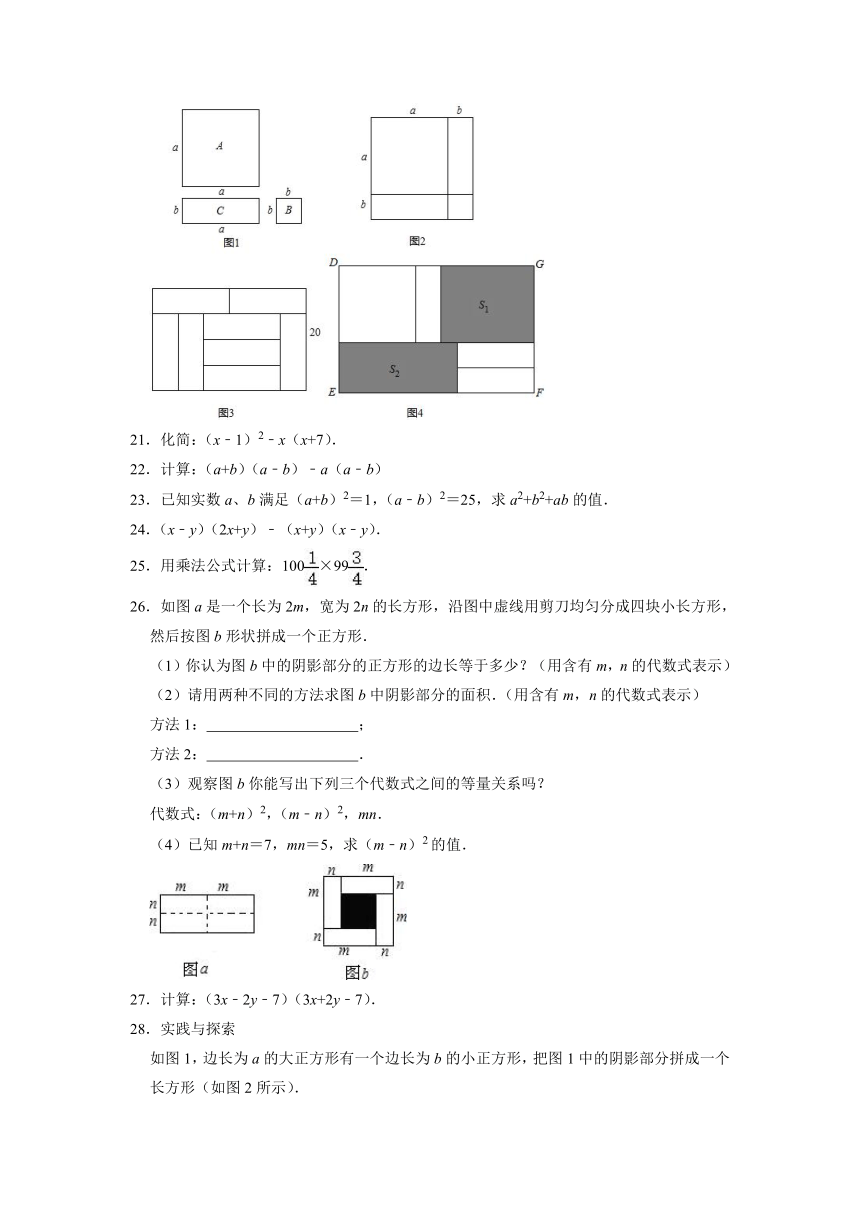
20.学习整式乘法时,老师拿出三种型号的卡片,如图1:A型卡片是边长为a的正方形,B型卡片是边长为b的正方形,C型卡片是长和宽分别为a,b的长方形.
(1)选取1张A型卡片,2张C型卡片,1张B型卡片,在纸上按照图2的方式拼成一个长为(a+b)的大正方形,通过不同方式表示大正方形的面积,可得到乘法公式: .
(2)若用图1中的8块C型长方形卡片可以拼成如图3所示的长方形,它的宽为20cm,请你求出每块长方形的面积.
(3)选取1张A型卡片,3张C型卡片按图4的方式不重叠地放在长方形DEFG框架内,已知GF的长度固定不变,DG的长度可以变化,图中两阴影部分(长方形)的面积分别表示为S1,S2,若S=S2﹣S1,则当a与b满足 时,S为定值,且定值为 .
21.化简:(x﹣1)2﹣x(x+7).
22.计算:(a+b)(a﹣b)﹣a(a﹣b)
23.已知实数a、b满足(a+b)2=1,(a﹣b)2=25,求a2+b2+ab的值.
24.(x﹣y)(2x+y)﹣(x+y)(x﹣y).
25.用乘法公式计算:100×99.
26.如图a是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图b形状拼成一个正方形.
(1)你认为图b中的阴影部分的正方形的边长等于多少?(用含有m,n的代数式表示)
(2)请用两种不同的方法求图b中阴影部分的面积.(用含有m,n的代数式表示)
方法1: ;
方法2: .
(3)观察图b你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m﹣n)2,mn.
(4)已知m+n=7,mn=5,求(m﹣n)2的值.
27.计算:(3x﹣2y﹣7)(3x+2y﹣7).
28.实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
29.乘法公式的探究及应用.
图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1:
方法2:
(2)观察图2请你写出下列三个代数式:(a+b)2,(a﹣b)2,ab之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a﹣b=5,ab=﹣6,求:a2+b2= ,(a+b)2=
②已知的值.
参考答案
1.解:A、因为正方形图案的边长7,同时还可用(x+y)来表示,故(x+y)2=x2+2xy+y2=72=49,正确;
B、由图象可知(x﹣y)2=4,即x2﹣2xy+y2=4,正确;
C、由(x+y)2=x2+2xy+y2=72=49和(x﹣y)2=x2﹣2xy+y2=4,可得2xy=,x2+y2=(x+y)2﹣2xy=49﹣=26.5≠25,错误;
D、由x+y=7,x﹣y=2,可得x=4.5,y=2.5,所以x2﹣y2=4.52﹣2.52=20.25﹣6.25=14,正确.
故选:C.
2.解:A:原式=(x+y)(y﹣x)=y2﹣x2,∴不符合题意;
B:原式=(﹣x+y)(﹣x﹣y)=(﹣x)2﹣y2=x2﹣y2,∴不符合题意;
C:原式=(﹣y﹣x)(﹣y+x)=(﹣y)2﹣x2=y2﹣x2,∴不符合题意;
D:原式=﹣(x﹣y)(x﹣y)=﹣(x﹣y)2,∴符合题意;
故选:D.
3.解:A、(﹣2b3)2=4b6,原计算错误,故此选项不符合题意;
B、(a﹣b)2=a2﹣2ab+b2,原计算错误,故此选项不符合题意;
C、2a2+a2=3a2,原计算正确,故此选项符合题意;
D、2a6÷2a2=a4,原计算错误,故此选项不符合题意.
故选:C.
4.解:矩形的面积为(a+6)(a﹣6)=a2﹣36,
∴矩形的面积比正方形的面积a2小了36平方米,
故选:C.
5.解:(2n+1)2﹣(2n﹣1)2
=[(2n+1)﹣(2n﹣1)][(2n+1)+(2n﹣1)]
=8n,
故当n是正整数时,(2n+1)2﹣(2n﹣1)2是8的倍数.
故选:D.
6.解:∵x+y=6,x2+y2=(x+y)2﹣2xy=20,
∴2xy=62﹣20=16,
∴xy=8,
∴(x﹣y)2=x2+y2﹣2xy=20﹣2×8=4,
∴x﹣y=±2,
故选:D.
7.解:①﹣a﹣b=﹣(a+b),正确;
②(﹣a﹣b)2=(a+b)2,正确;
③|﹣a﹣b|=a+b,故原说法错误;
④(﹣a﹣b)3=﹣(a+b)3,故原说法错误.
其中不正确的有③④,
故选:B.
8.解:选项A:2482+248×52+522不符合完全平方公式的特征且计算错误,完全平方公式的中间一项为2×248×52,所以不符合题意;
选项B:2482﹣248×48﹣482不符合完全平方公式特征且计算错误,最后一项应为+482,所以不符合题意;
选项C:2482+2×248×52+522=(248+52)2=3002,所以符合题意;
选项D:2482﹣2×248×48﹣482=2002不符合完全平方公式特征且计算错误,最后一项应为+482,所以不符合题意.
故选:C.
9.解:矩形的面积为(a+6)(a﹣6)=a2﹣36,
∴矩形的面积比正方形的面积a2小了36平方米,
故选:C.
10.解:原式=(a+b)2﹣9=a2+2ab+b2﹣9.
故选:C.
11.解:找规律发现(a+b)4的第四项系数为4=3+1;
(a+b)5的第四项系数为10=6+4;
(a+b)6的第四项系数为20=10+10;
(a+b)7的第四项系数为35=15+20;
∴(a+b)8第四项系数为21+35=56.
故选:B.
12.解:(1)由图可知:一块甲种纸片的面积为a2,一块乙种纸片的面积为b2,一块丙种纸片面积为ab,
∴取甲、乙纸片各1块,其面积和为a2+b2,
故答案为:a2+b2;
(2)设取丙种纸片x块才能用它们拼成一个新的正方形,(x≥0)
∴a2+4b2+xab是一个完全平方式,
∴x为4,
故答案为:4.
13.解:∵x﹣2y=﹣2,x+2y=3,
∴x2﹣4y2=(x+2y)(x﹣2y)=3×(﹣2)=﹣6,
故答案为:﹣6.
14.解:∵a=b+2,
∴a﹣b=2,
∴a2﹣2ab+b2=(a﹣b)2=22=4.
故答案为:4
15.解:法一:(x+y)2=x2+2xy+y2=1,(x﹣y)2=x2﹣2xy+y2=4,
两式相减得4xy=﹣3,
解得xy=﹣,
则P=﹣.
法二:由题可得,
解之得:,
∴P=xy=﹣,
故答案为:﹣.
16.解:∵a+b=5,a﹣b=3,
∴a2﹣b2
=(a+b)(a﹣b)
=5×3
=15,
故答案为:15.
17.解:∵=m2﹣2+=9,
∴m2+=11,
故答案为11.
18.解:观察图形,可知:(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
故答案为:a5+5a4b+10a3b2+10a2b3+5ab4+b5.
19.解:(a﹣b)(a+b)=a2﹣b2;
(a﹣b)(a2+ab+b2)=a3﹣b3;
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4;
…
可得到(a﹣b)(a2022+a2021b+…+ab2021+b2022)=a2023﹣b2023,
故答案为:a2023﹣b2023
20.解:(1)方法1:大正方形的面积为(a+b)2,
方法2:图2中四部分的面积和为:a2+2ab+b2,
因此有(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2.
(2)设每块C型卡片的宽为xcm,长为ycm,
根据题意得 x+y=20,4x=20,
解得 x=5,y=15,
所以每块长方形材料的面积是:5×15=75(cm2).
(3)设DG长为x.
∵S1=a[x﹣(a+b)]=ax﹣a2﹣ab,S2=2b(x﹣a)=2bx﹣2ab,
∴S=S2﹣S1=(2b﹣a)x+a2﹣ab,
由题意得,若S为定值,则S将不随x的变化而变化,
可知当2b﹣a=0时,即a=2b时,S=a2﹣ab为定值,
故答案为:a=2b,a2﹣ab.
21.解:(x﹣1)2﹣x(x+7)
=x2﹣2x+1﹣x2﹣7x
=﹣9x+1.
22.解:原式=a2﹣b2﹣a2+ab=ab﹣b2
23.解:∵(a+b)2=1,(a﹣b)2=25,
∴a2+b2+2ab=1,a2+b2﹣2ab=25.
∴4ab=﹣24,ab=﹣6,
∴a2+b2+ab=(a+b)2﹣ab=1﹣(﹣6)=7.
24.解:原式=2x2﹣xy﹣y2﹣x2+y2=x2﹣xy.
25.解:100×99
=
=
=10000﹣
=9999.
26.解:(1)阴影部分的正方形边长是:m﹣n;
(2)阴影部分的面积就等于边长为m﹣n的小正方形的面积,
方法1:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,即(m+n)2﹣4mn;
方法2:边长为m﹣n的正方形的面积,即(m﹣n)2;
故答案为:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,即(m+n)2﹣4mn;边长为m﹣n的正方形的面积,即(m﹣n)2;
(3)由(2)可得:(m+n)2=(m﹣n)2+4mn;
(4)(m﹣n)2=(m+n)2﹣4mn=49﹣4×5==49﹣20=29.
27.解:原式=(3x﹣7)2﹣(2y)2
=9x2﹣42x+49﹣4y2.
28.解:(1)图1中阴影部分的面积为两个正方形的面积差,即a2﹣b2,
图2中的阴影部分是长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
故答案为:A;
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
又∵2a+b=6,
∴6(2a﹣b)=24,
即2a﹣b=4,
故答案为:4;
②∵1002﹣992=(100+99)(100﹣99)=100+99,
982﹣972=(98+97)(98﹣97)=98+97,
…
22﹣12=(2+1)(2﹣1)=2+1,
∴原式=100+99+98+97+…+4+3+2+1=5050.
29.解:(1)阴影部分是正方形,正方形的边长是m﹣n,即阴影部分的面积是(m﹣n)2,
又∵阴影部分的面积S=(m+n)2﹣4mn,
故答案为:(m﹣n)2,(m+n)2﹣4mn.
(2)(a﹣b)2=(a+b)2﹣4ab,
故答案为:(a﹣b)2=(a+b)2﹣4ab.
(3)①∵a﹣b=5,ab=﹣6,
∴(a﹣b)2=52
∴a2﹣2ab+b2=25,
a2+b2=25+2ab=25﹣12=13,
故答案为:13.
(a+b)2=(a﹣b)2+4ab=52+4×(﹣6)=1.
故答案为:1.
=
=
=(32﹣2)2﹣2
=47.
1.如图,由4个全等的小长方形与1个小正方形密铺成正方形图案,该图案的面积为49,小正方形的面积为4,若分别用x,y(x>y)表示小长方形的长和宽,则下列关系式中不正确的是( )
A.x2+2xy+y2=49 B.x2﹣2xy+y2=4
C.x2+y2=25 D.x2﹣y2=14
2.下列各式中不能用平方差公式计算的是( )
A.(x+y)(﹣x+y) B.(﹣x+y)(﹣x﹣y)
C.(﹣x﹣y)(x﹣y) D.(x﹣y)(﹣x+y)
3.下列运算正确的是( )
A.(﹣2b3)2=﹣4b6 B.(a﹣b)2=a2﹣b2
C.2a2+a2=3a2 D.2a6÷2a2=a3
4.从前,古希腊一位庄园主把一块边长为a米(a≥6)的正方形土地租给租户王老汉,第二年,他对王老汉说:“我把这块地的一边增加6米,相邻的另边减少6米,变成矩形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得王老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
5.当n为正整数时,代数式(2n+1)2﹣(2n﹣1)2一定是下面哪个数的倍数( )
A.3 B.5 C.7 D.8
6.若x+y=6,x2+y2=20,求x﹣y的值是( )
A.2 B.﹣2 C.4 D.±2
7.关于﹣a﹣b进行的变形或运算:①﹣a﹣b=﹣(a+b);②(﹣a﹣b)2=(a+b)2;③|﹣a﹣b|=a﹣b;④(﹣a﹣b)3=﹣(a﹣b)3.其中不正确的是( )
A.①② B.③④ C.①③ D.②④
8.利用乘法公式判断,下列等式何者成立?( )
A.2482+248×52+522=3002
B.2482﹣248×48﹣482=2002
C.2482+2×248×52+522=3002
D.2482﹣2×248×48﹣482=2002
9.从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加6米,相邻的另一边减少6米,变成矩形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
10.计算(a+b﹣3)(a+b+3)的结果是( )
A.a2+b2﹣9 B.a2﹣b2+6b﹣9
C.a2+2ab+b2﹣9 D.a2﹣b2﹣6b+9
11.我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”
根据”杨辉三角”请计算(a+b)8的展开式中从左起第四项的系数为( )
A.84 B.56 C.35 D.28
12.现有甲、乙、丙三种不同的矩形纸片(边长如图).
(1)取甲、乙纸片各1块,其面积和为 ;
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲纸片1块,再取乙纸片4块,还需取丙纸片 块.
13.若x、y满足,则代数式x2﹣4y2的值为 .
14.若a=b+2,则代数式a2﹣2ab+b2的值为 .
15.设M=x+y,N=x﹣y,P=xy.若M=1,N=2,则P= .
16.若a+b=5,a﹣b=3,则a2﹣b2= .
17.若m﹣=3,则m2+= .
18.杨辉三角,又称贾宪三角,是二项式系数在三角形中的一种几何排列,如图,观察下面的杨辉三角:
按照前面的规律,则(a+b)5= .
19.观察下列各式的规律:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
…
可得到(a﹣b)(a2022+a2021b+…+ab2021+b2022)= .
20.学习整式乘法时,老师拿出三种型号的卡片,如图1:A型卡片是边长为a的正方形,B型卡片是边长为b的正方形,C型卡片是长和宽分别为a,b的长方形.
(1)选取1张A型卡片,2张C型卡片,1张B型卡片,在纸上按照图2的方式拼成一个长为(a+b)的大正方形,通过不同方式表示大正方形的面积,可得到乘法公式: .
(2)若用图1中的8块C型长方形卡片可以拼成如图3所示的长方形,它的宽为20cm,请你求出每块长方形的面积.
(3)选取1张A型卡片,3张C型卡片按图4的方式不重叠地放在长方形DEFG框架内,已知GF的长度固定不变,DG的长度可以变化,图中两阴影部分(长方形)的面积分别表示为S1,S2,若S=S2﹣S1,则当a与b满足 时,S为定值,且定值为 .
21.化简:(x﹣1)2﹣x(x+7).
22.计算:(a+b)(a﹣b)﹣a(a﹣b)
23.已知实数a、b满足(a+b)2=1,(a﹣b)2=25,求a2+b2+ab的值.
24.(x﹣y)(2x+y)﹣(x+y)(x﹣y).
25.用乘法公式计算:100×99.
26.如图a是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图b形状拼成一个正方形.
(1)你认为图b中的阴影部分的正方形的边长等于多少?(用含有m,n的代数式表示)
(2)请用两种不同的方法求图b中阴影部分的面积.(用含有m,n的代数式表示)
方法1: ;
方法2: .
(3)观察图b你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m﹣n)2,mn.
(4)已知m+n=7,mn=5,求(m﹣n)2的值.
27.计算:(3x﹣2y﹣7)(3x+2y﹣7).
28.实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
29.乘法公式的探究及应用.
图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1:
方法2:
(2)观察图2请你写出下列三个代数式:(a+b)2,(a﹣b)2,ab之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a﹣b=5,ab=﹣6,求:a2+b2= ,(a+b)2=
②已知的值.
参考答案
1.解:A、因为正方形图案的边长7,同时还可用(x+y)来表示,故(x+y)2=x2+2xy+y2=72=49,正确;
B、由图象可知(x﹣y)2=4,即x2﹣2xy+y2=4,正确;
C、由(x+y)2=x2+2xy+y2=72=49和(x﹣y)2=x2﹣2xy+y2=4,可得2xy=,x2+y2=(x+y)2﹣2xy=49﹣=26.5≠25,错误;
D、由x+y=7,x﹣y=2,可得x=4.5,y=2.5,所以x2﹣y2=4.52﹣2.52=20.25﹣6.25=14,正确.
故选:C.
2.解:A:原式=(x+y)(y﹣x)=y2﹣x2,∴不符合题意;
B:原式=(﹣x+y)(﹣x﹣y)=(﹣x)2﹣y2=x2﹣y2,∴不符合题意;
C:原式=(﹣y﹣x)(﹣y+x)=(﹣y)2﹣x2=y2﹣x2,∴不符合题意;
D:原式=﹣(x﹣y)(x﹣y)=﹣(x﹣y)2,∴符合题意;
故选:D.
3.解:A、(﹣2b3)2=4b6,原计算错误,故此选项不符合题意;
B、(a﹣b)2=a2﹣2ab+b2,原计算错误,故此选项不符合题意;
C、2a2+a2=3a2,原计算正确,故此选项符合题意;
D、2a6÷2a2=a4,原计算错误,故此选项不符合题意.
故选:C.
4.解:矩形的面积为(a+6)(a﹣6)=a2﹣36,
∴矩形的面积比正方形的面积a2小了36平方米,
故选:C.
5.解:(2n+1)2﹣(2n﹣1)2
=[(2n+1)﹣(2n﹣1)][(2n+1)+(2n﹣1)]
=8n,
故当n是正整数时,(2n+1)2﹣(2n﹣1)2是8的倍数.
故选:D.
6.解:∵x+y=6,x2+y2=(x+y)2﹣2xy=20,
∴2xy=62﹣20=16,
∴xy=8,
∴(x﹣y)2=x2+y2﹣2xy=20﹣2×8=4,
∴x﹣y=±2,
故选:D.
7.解:①﹣a﹣b=﹣(a+b),正确;
②(﹣a﹣b)2=(a+b)2,正确;
③|﹣a﹣b|=a+b,故原说法错误;
④(﹣a﹣b)3=﹣(a+b)3,故原说法错误.
其中不正确的有③④,
故选:B.
8.解:选项A:2482+248×52+522不符合完全平方公式的特征且计算错误,完全平方公式的中间一项为2×248×52,所以不符合题意;
选项B:2482﹣248×48﹣482不符合完全平方公式特征且计算错误,最后一项应为+482,所以不符合题意;
选项C:2482+2×248×52+522=(248+52)2=3002,所以符合题意;
选项D:2482﹣2×248×48﹣482=2002不符合完全平方公式特征且计算错误,最后一项应为+482,所以不符合题意.
故选:C.
9.解:矩形的面积为(a+6)(a﹣6)=a2﹣36,
∴矩形的面积比正方形的面积a2小了36平方米,
故选:C.
10.解:原式=(a+b)2﹣9=a2+2ab+b2﹣9.
故选:C.
11.解:找规律发现(a+b)4的第四项系数为4=3+1;
(a+b)5的第四项系数为10=6+4;
(a+b)6的第四项系数为20=10+10;
(a+b)7的第四项系数为35=15+20;
∴(a+b)8第四项系数为21+35=56.
故选:B.
12.解:(1)由图可知:一块甲种纸片的面积为a2,一块乙种纸片的面积为b2,一块丙种纸片面积为ab,
∴取甲、乙纸片各1块,其面积和为a2+b2,
故答案为:a2+b2;
(2)设取丙种纸片x块才能用它们拼成一个新的正方形,(x≥0)
∴a2+4b2+xab是一个完全平方式,
∴x为4,
故答案为:4.
13.解:∵x﹣2y=﹣2,x+2y=3,
∴x2﹣4y2=(x+2y)(x﹣2y)=3×(﹣2)=﹣6,
故答案为:﹣6.
14.解:∵a=b+2,
∴a﹣b=2,
∴a2﹣2ab+b2=(a﹣b)2=22=4.
故答案为:4
15.解:法一:(x+y)2=x2+2xy+y2=1,(x﹣y)2=x2﹣2xy+y2=4,
两式相减得4xy=﹣3,
解得xy=﹣,
则P=﹣.
法二:由题可得,
解之得:,
∴P=xy=﹣,
故答案为:﹣.
16.解:∵a+b=5,a﹣b=3,
∴a2﹣b2
=(a+b)(a﹣b)
=5×3
=15,
故答案为:15.
17.解:∵=m2﹣2+=9,
∴m2+=11,
故答案为11.
18.解:观察图形,可知:(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
故答案为:a5+5a4b+10a3b2+10a2b3+5ab4+b5.
19.解:(a﹣b)(a+b)=a2﹣b2;
(a﹣b)(a2+ab+b2)=a3﹣b3;
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4;
…
可得到(a﹣b)(a2022+a2021b+…+ab2021+b2022)=a2023﹣b2023,
故答案为:a2023﹣b2023
20.解:(1)方法1:大正方形的面积为(a+b)2,
方法2:图2中四部分的面积和为:a2+2ab+b2,
因此有(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2.
(2)设每块C型卡片的宽为xcm,长为ycm,
根据题意得 x+y=20,4x=20,
解得 x=5,y=15,
所以每块长方形材料的面积是:5×15=75(cm2).
(3)设DG长为x.
∵S1=a[x﹣(a+b)]=ax﹣a2﹣ab,S2=2b(x﹣a)=2bx﹣2ab,
∴S=S2﹣S1=(2b﹣a)x+a2﹣ab,
由题意得,若S为定值,则S将不随x的变化而变化,
可知当2b﹣a=0时,即a=2b时,S=a2﹣ab为定值,
故答案为:a=2b,a2﹣ab.
21.解:(x﹣1)2﹣x(x+7)
=x2﹣2x+1﹣x2﹣7x
=﹣9x+1.
22.解:原式=a2﹣b2﹣a2+ab=ab﹣b2
23.解:∵(a+b)2=1,(a﹣b)2=25,
∴a2+b2+2ab=1,a2+b2﹣2ab=25.
∴4ab=﹣24,ab=﹣6,
∴a2+b2+ab=(a+b)2﹣ab=1﹣(﹣6)=7.
24.解:原式=2x2﹣xy﹣y2﹣x2+y2=x2﹣xy.
25.解:100×99
=
=
=10000﹣
=9999.
26.解:(1)阴影部分的正方形边长是:m﹣n;
(2)阴影部分的面积就等于边长为m﹣n的小正方形的面积,
方法1:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,即(m+n)2﹣4mn;
方法2:边长为m﹣n的正方形的面积,即(m﹣n)2;
故答案为:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,即(m+n)2﹣4mn;边长为m﹣n的正方形的面积,即(m﹣n)2;
(3)由(2)可得:(m+n)2=(m﹣n)2+4mn;
(4)(m﹣n)2=(m+n)2﹣4mn=49﹣4×5==49﹣20=29.
27.解:原式=(3x﹣7)2﹣(2y)2
=9x2﹣42x+49﹣4y2.
28.解:(1)图1中阴影部分的面积为两个正方形的面积差,即a2﹣b2,
图2中的阴影部分是长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
故答案为:A;
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
又∵2a+b=6,
∴6(2a﹣b)=24,
即2a﹣b=4,
故答案为:4;
②∵1002﹣992=(100+99)(100﹣99)=100+99,
982﹣972=(98+97)(98﹣97)=98+97,
…
22﹣12=(2+1)(2﹣1)=2+1,
∴原式=100+99+98+97+…+4+3+2+1=5050.
29.解:(1)阴影部分是正方形,正方形的边长是m﹣n,即阴影部分的面积是(m﹣n)2,
又∵阴影部分的面积S=(m+n)2﹣4mn,
故答案为:(m﹣n)2,(m+n)2﹣4mn.
(2)(a﹣b)2=(a+b)2﹣4ab,
故答案为:(a﹣b)2=(a+b)2﹣4ab.
(3)①∵a﹣b=5,ab=﹣6,
∴(a﹣b)2=52
∴a2﹣2ab+b2=25,
a2+b2=25+2ab=25﹣12=13,
故答案为:13.
(a+b)2=(a﹣b)2+4ab=52+4×(﹣6)=1.
故答案为:1.
=
=
=(32﹣2)2﹣2
=47.
