2021-2022学年人教版九年级数学下册27.1图形的相似 同步达标训练(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.1图形的相似 同步达标训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 170.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 08:47:56 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学下册《27.1图形的相似》同步达标训练(附答案)
1.下列说法正确的是( )
A.矩形都是相似图形
B.各角对应相等的两个五边形相似
C.等边三角形都是相似三角形
D.各边对应成比例的两个六边形相似
2.已知,那么下列式子中一定成立的是( )
A.x+y=5 B.2x=3y C. D.
3.下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
4.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
A.AB2=AC BC B.BC2=AC BC C.AC=BC D.BC=AC
5.如图,△ABC中,DE∥BC,=,AE=2cm,则AC的长是( )
A.2cm B.4cm C.6cm D.8cm
6.如图,AB∥CD,AC与BD相交于点O,若AO=3,BO=6,CO=2,则BD的长为( )
A.4 B.10 C.11 D.12
7.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
8.已知==,且a+b﹣2c=6,则a的值为 .
9.已知2x=3y(y≠0),那么= .
10.4与9的比例中项是 .
11.已知点P在线段AB上,且AP:BP=2:3,那么AB:PB= .
12.在比例尺是1:15000000的地图上,测得甲乙两地的距离是2厘米,那么甲乙两地的实际距离是 千米.
13.线段AB=10,点P是AB的黄金分割点,且AP>BP,则AP= (用根式表示).
14.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC的长是 .
15.如图,AB∥CD,AD与BC相交于点O.若=,AD=15,则AO的长为 .
16.如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、C、E和点B、D、F,如果AC:CE=3:5,BF=9,那么DF= .
17.如图,已知BE平分∠ABC,DE∥BC,AD=3,DE=2,AC=4,则AE= .
18.如图,△ABC中,DE∥FG∥BC,AD:DF:FB=2:3:4,若EG=4,则AC= .
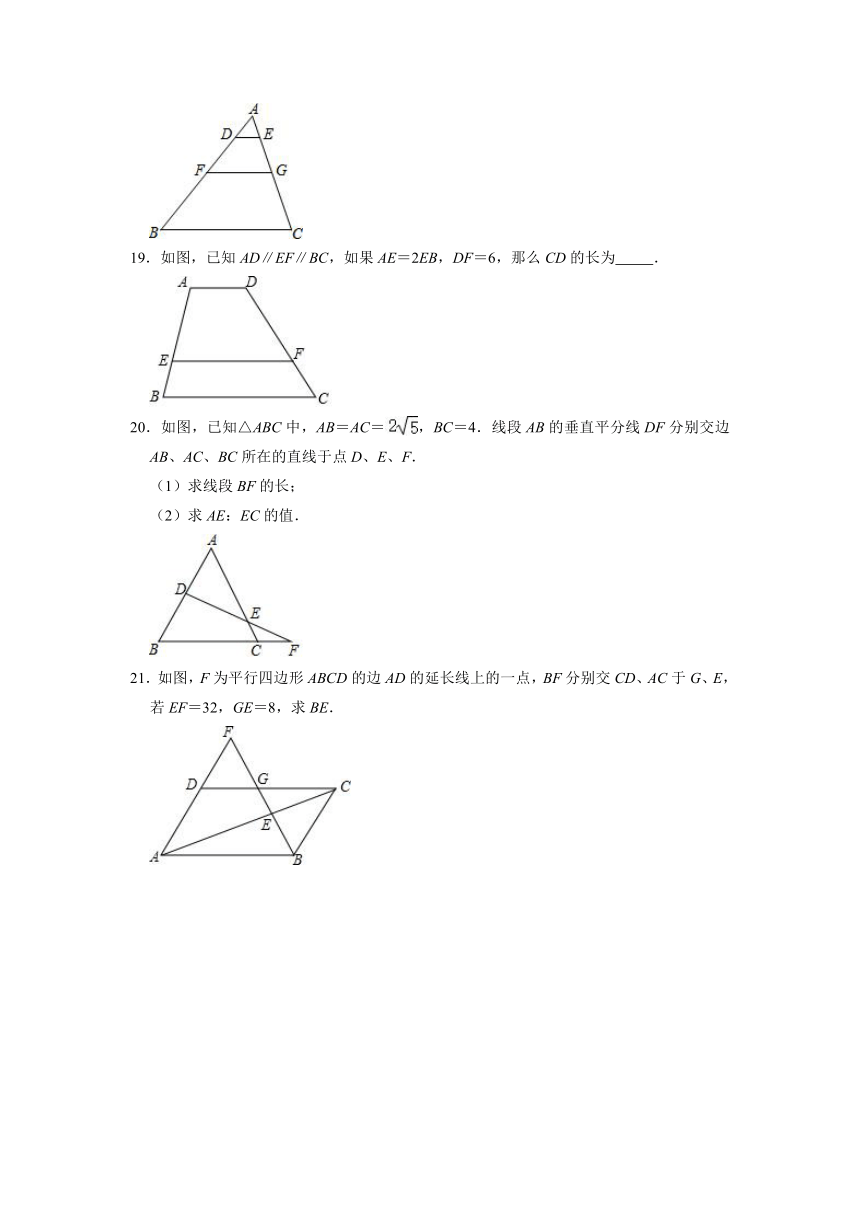
19.如图,已知AD∥EF∥BC,如果AE=2EB,DF=6,那么CD的长为 .
20.如图,已知△ABC中,AB=AC=,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
(1)求线段BF的长;
(2)求AE:EC的值.
21.如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交CD、AC于G、E,若EF=32,GE=8,求BE.
参考答案
1.解:A.矩形对应角相等,对应边不一定成比例,所以不一定是相似图形,故本选项错误;
B. 各角对应相等的两个五边形相似,对应角相等,对应边不一定成比例,所以不一定是相似图形,故本选项错误;
C. 等边三角形对应角相等,对应边成比例,所以是相似三角形,故本选项正确;
D. 各边对应成比例的六边形对应角不一定相等,所以不一定是相似六边形,故本选项错误;
故选:C.
2.解:∵,∴x+y=5不一定成立,A错误;
∵,∴3x=2y,∴2x=3y不成立,B错误;
∵,∴=,C错误,D正确,
故选:D.
3.解:根据如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.
所给选项中,只有D符合,3×18=6×9,故选:D.
4.解:∵点C是线段AB的黄金分割点且AC>BC,
∴=,即AC2=BC AB,故A、B错误;
AC=AB,故C错误;
BC=AC,故D正确;
故选:D.
5.解:∵DE∥BC,
∴=,
∵,AE=2cm,
∴=,
∴AC=6(cm),
故选:C.
6.解:∵AB∥CD,
∴=,
∵AO=3,BO=6,CO=2,
∴DO=4,
∴BD=4+6=10,
故选:B.
7.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
8.解:∵==,
∴设a=6x,b=5x,c=4x,
∵a+b﹣2c=6,
∴6x+5x﹣8x=6,
解得:x=2,
故a=12.
故答案为:12.
9.解:由2x=3y(y≠0),
可得:,
所以,
故答案为:
10.解:设它们的比例中项是x,
则x2=4×9,
x=±6.
故答案为±6.
11.解:由题意AP:PB=2:3,
AB:PB=(AP+PB):PB=(2+3):3=5:3;
故答案为:5:3;
12.解:设这两地的实际距离是xcm,
根据题意得:=,
解得:x=30000000,
∵30000000cm=300km,
∴这两地的实际距离是300km.
故答案为:300.
13.解:∵点P是AB的黄金分割点,AP>BP,
∴AP=AB×,
∵线段AB=10,
∴AP=10×=5﹣5;
故答案为:5﹣5.
14.解:∵DE∥AC,
∴DB:AB=BE:BC,
∵DB=4,AB=6,BE=3,
∴4:6=3:BC,
解得:BC=,
∴EC=BC﹣BE=﹣3=.
故答案为:.
15.解:∵AB∥CD,
∴,即,
解得,AO=6,
故答案为:6.
16.解:∵AC:CE=3:5,
∴AC:AE=3:8,
∵AB∥CD∥EF,
∴,
∴BD=,
∴DF=,
故答案为:.
17.解:如图,∵BE平分∠ABC,DE∥BC,
∴∠DBE=∠CBE,∠DEB=∠CBE,
∴∠DBE=∠DEB,
∴DB=DE=2,AB=AD+DB=5;
∵DE∥BC,
∴△ADE∽△ABC,
∴,而AC=4,AD=3,
∴AE=2.4,
故答案为2.4.
18.解:∵DE∥FG∥BC,
∴AE:EG:GC=AD:DF:FB=2:3:4,
∵EG=4,
∴AE=,GC=,
∴AC=AE+EG+GC=12,
故答案为:12.
19.解:∵AD∥EF∥BC,==2,
∴DF=6,
∴FC=3,DC=DF+FC=9.
故答案是:9.
20.解:(1)作AH⊥BC于H,如图,
∵AB=AC=,
∴BH=CH=BC=2,
在Rt△ABH中,AH==4,
∵DF垂直平分AB,
∴BD=,∠BDF=90°
∵∠ABH=∠FBD,
∴Rt△FBD∽Rt△ABH,
∴==,即==,
∴BF=5,DF=2;
(2)作CG∥AB交DF于G,如图,
∵BF=5,BC=4,
∴CF=1,
∵CG∥BD,
∴==,
∵CG∥AD,
∴===5.
21.解:∵AD∥BC,
∴△AFE∽△CBE,
∴==,
∵GC∥AB,
∴△CGE∽△ABE,
∴=,
∴=,
∴BE2=EF GE=32×8=256,
解得:BE=±16(负数舍去),
故BE=16.
1.下列说法正确的是( )
A.矩形都是相似图形
B.各角对应相等的两个五边形相似
C.等边三角形都是相似三角形
D.各边对应成比例的两个六边形相似
2.已知,那么下列式子中一定成立的是( )
A.x+y=5 B.2x=3y C. D.
3.下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
4.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
A.AB2=AC BC B.BC2=AC BC C.AC=BC D.BC=AC
5.如图,△ABC中,DE∥BC,=,AE=2cm,则AC的长是( )
A.2cm B.4cm C.6cm D.8cm
6.如图,AB∥CD,AC与BD相交于点O,若AO=3,BO=6,CO=2,则BD的长为( )
A.4 B.10 C.11 D.12
7.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
8.已知==,且a+b﹣2c=6,则a的值为 .
9.已知2x=3y(y≠0),那么= .
10.4与9的比例中项是 .
11.已知点P在线段AB上,且AP:BP=2:3,那么AB:PB= .
12.在比例尺是1:15000000的地图上,测得甲乙两地的距离是2厘米,那么甲乙两地的实际距离是 千米.
13.线段AB=10,点P是AB的黄金分割点,且AP>BP,则AP= (用根式表示).
14.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC的长是 .
15.如图,AB∥CD,AD与BC相交于点O.若=,AD=15,则AO的长为 .
16.如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、C、E和点B、D、F,如果AC:CE=3:5,BF=9,那么DF= .
17.如图,已知BE平分∠ABC,DE∥BC,AD=3,DE=2,AC=4,则AE= .
18.如图,△ABC中,DE∥FG∥BC,AD:DF:FB=2:3:4,若EG=4,则AC= .
19.如图,已知AD∥EF∥BC,如果AE=2EB,DF=6,那么CD的长为 .
20.如图,已知△ABC中,AB=AC=,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
(1)求线段BF的长;
(2)求AE:EC的值.
21.如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交CD、AC于G、E,若EF=32,GE=8,求BE.
参考答案
1.解:A.矩形对应角相等,对应边不一定成比例,所以不一定是相似图形,故本选项错误;
B. 各角对应相等的两个五边形相似,对应角相等,对应边不一定成比例,所以不一定是相似图形,故本选项错误;
C. 等边三角形对应角相等,对应边成比例,所以是相似三角形,故本选项正确;
D. 各边对应成比例的六边形对应角不一定相等,所以不一定是相似六边形,故本选项错误;
故选:C.
2.解:∵,∴x+y=5不一定成立,A错误;
∵,∴3x=2y,∴2x=3y不成立,B错误;
∵,∴=,C错误,D正确,
故选:D.
3.解:根据如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.
所给选项中,只有D符合,3×18=6×9,故选:D.
4.解:∵点C是线段AB的黄金分割点且AC>BC,
∴=,即AC2=BC AB,故A、B错误;
AC=AB,故C错误;
BC=AC,故D正确;
故选:D.
5.解:∵DE∥BC,
∴=,
∵,AE=2cm,
∴=,
∴AC=6(cm),
故选:C.
6.解:∵AB∥CD,
∴=,
∵AO=3,BO=6,CO=2,
∴DO=4,
∴BD=4+6=10,
故选:B.
7.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
8.解:∵==,
∴设a=6x,b=5x,c=4x,
∵a+b﹣2c=6,
∴6x+5x﹣8x=6,
解得:x=2,
故a=12.
故答案为:12.
9.解:由2x=3y(y≠0),
可得:,
所以,
故答案为:
10.解:设它们的比例中项是x,
则x2=4×9,
x=±6.
故答案为±6.
11.解:由题意AP:PB=2:3,
AB:PB=(AP+PB):PB=(2+3):3=5:3;
故答案为:5:3;
12.解:设这两地的实际距离是xcm,
根据题意得:=,
解得:x=30000000,
∵30000000cm=300km,
∴这两地的实际距离是300km.
故答案为:300.
13.解:∵点P是AB的黄金分割点,AP>BP,
∴AP=AB×,
∵线段AB=10,
∴AP=10×=5﹣5;
故答案为:5﹣5.
14.解:∵DE∥AC,
∴DB:AB=BE:BC,
∵DB=4,AB=6,BE=3,
∴4:6=3:BC,
解得:BC=,
∴EC=BC﹣BE=﹣3=.
故答案为:.
15.解:∵AB∥CD,
∴,即,
解得,AO=6,
故答案为:6.
16.解:∵AC:CE=3:5,
∴AC:AE=3:8,
∵AB∥CD∥EF,
∴,
∴BD=,
∴DF=,
故答案为:.
17.解:如图,∵BE平分∠ABC,DE∥BC,
∴∠DBE=∠CBE,∠DEB=∠CBE,
∴∠DBE=∠DEB,
∴DB=DE=2,AB=AD+DB=5;
∵DE∥BC,
∴△ADE∽△ABC,
∴,而AC=4,AD=3,
∴AE=2.4,
故答案为2.4.
18.解:∵DE∥FG∥BC,
∴AE:EG:GC=AD:DF:FB=2:3:4,
∵EG=4,
∴AE=,GC=,
∴AC=AE+EG+GC=12,
故答案为:12.
19.解:∵AD∥EF∥BC,==2,
∴DF=6,
∴FC=3,DC=DF+FC=9.
故答案是:9.
20.解:(1)作AH⊥BC于H,如图,
∵AB=AC=,
∴BH=CH=BC=2,
在Rt△ABH中,AH==4,
∵DF垂直平分AB,
∴BD=,∠BDF=90°
∵∠ABH=∠FBD,
∴Rt△FBD∽Rt△ABH,
∴==,即==,
∴BF=5,DF=2;
(2)作CG∥AB交DF于G,如图,
∵BF=5,BC=4,
∴CF=1,
∵CG∥BD,
∴==,
∵CG∥AD,
∴===5.
21.解:∵AD∥BC,
∴△AFE∽△CBE,
∴==,
∵GC∥AB,
∴△CGE∽△ABE,
∴=,
∴=,
∴BE2=EF GE=32×8=256,
解得:BE=±16(负数舍去),
故BE=16.
