2021-2022学年人教版九年级数学下册27.2相似三角形 同步达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2相似三角形 同步达标测评(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 216.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 09:06:08 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学下册《27.2相似三角形》同步达标测评(附答案)
一.选择题(共8小题,满分40分)
1.将一个五边形改成与它相似的五边形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
A.9倍 B.3倍 C.81倍 D.18倍
2.下列说法中,正确的是( )
A.两个矩形相似 B.两个梯形相似
C.两个正方形相似 D.两个平行四边形相似
3.若两个相似三角形的相似比为1:2,则它们面积的比为( )
A.2:1 B.1: C.1:4 D.1:5
4.已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为( )
A.1:4 B.4:1 C.1:2 D.2:1
5.如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
A.∠DAC=∠ABC B.AC是∠BCD的平分线
C.AC2=BC CD D.=
6.如图,已知P是△ABC边AB上的一点,连接CP.以下条件中不能判定△ACP∽△ABC的是( )
A.∠ACP=∠B B.∠APC=∠ACB C.AC2=AP AB D.=
7.如图 ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于( )
A.2:5 B.3:5 C.2:3 D.5:7
8.如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )
A.7.2 cm B.5.4 cm C.3.6 cm D.0.6 cm
二.填空题(共8小题,满分40分)
9.一个四边形的各边之比为1:2:3:4,和它相似的另一个四边形的最小边长为5cm,则它的最大边长为 cm.
10.若两个相似多边形面积比为4:9,则它们的周长比是 .
11.若两个相似三角形的周长之比为2:3,较小三角形的面积为8cm2,则较大三角形面积是 cm2.
12.如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= .
13.如图,△ABC中,∠AED=∠B,AD=2,DB=4,AE=3,则EC= .
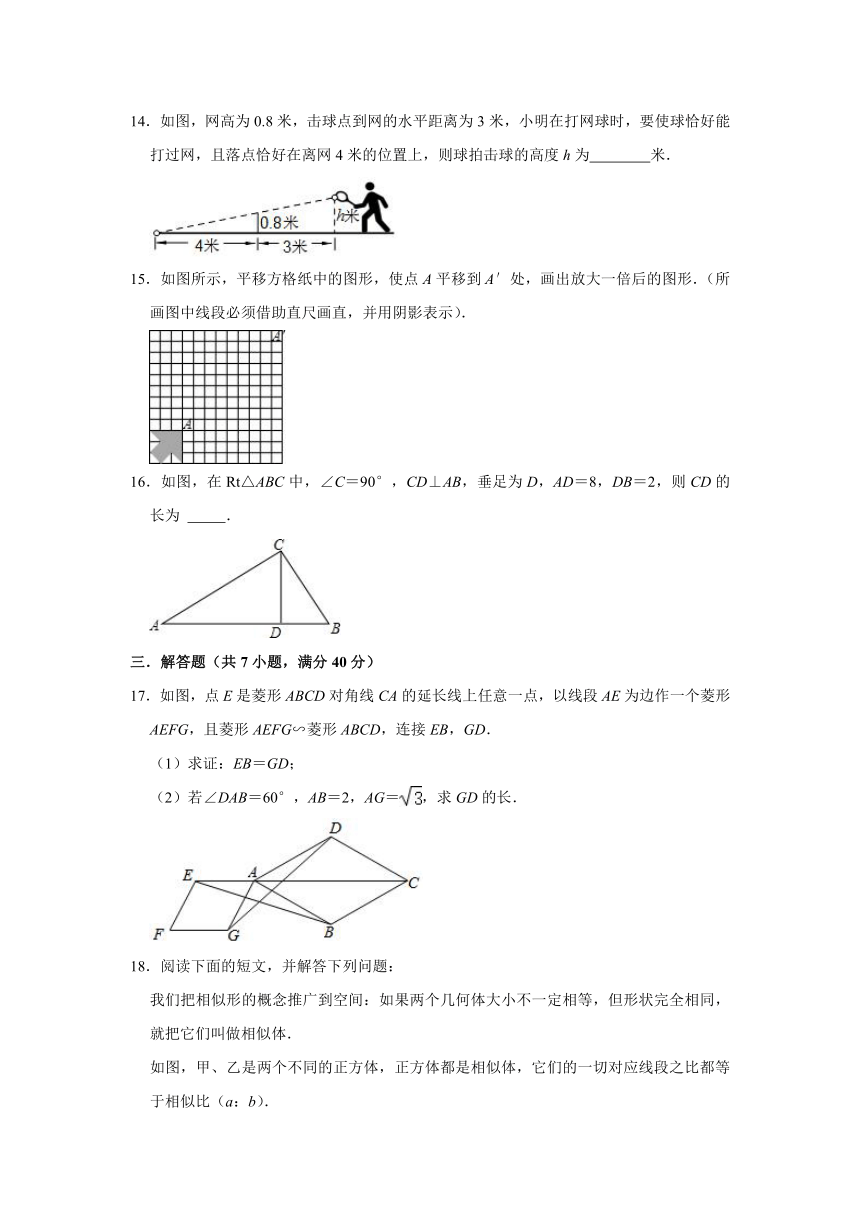
14.如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为 米.
15.如图所示,平移方格纸中的图形,使点A平移到A′处,画出放大一倍后的图形.(所画图中线段必须借助直尺画直,并用阴影表示).
16.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为 .
三.解答题(共7小题,满分40分)
17.如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=,求GD的长.
18.阅读下面的短文,并解答下列问题:
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比(a:b).
设S甲、S乙分别表示这两个正方体的表面积,则==()2
又设V甲、V乙分别表示这两个正方体的体积,则==()3
(1)下列几何体中,一定属于相似体的是(A)
A.两个球体B.两个锥体C.两个圆柱体D.两个长方体
(2)请归纳出相似体的三条主要性质:
①相似体的一切对应线段(或弧)长的比等于 ;
②相似体表面积的比等于 ;
③相似体体积比等于 .
(3)假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为1.1米,体重为18千克,到了初三时,身高为1.65米,问他的体重是多少?(不考虑不同时期人体平均密度的变化)
19.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
20.如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
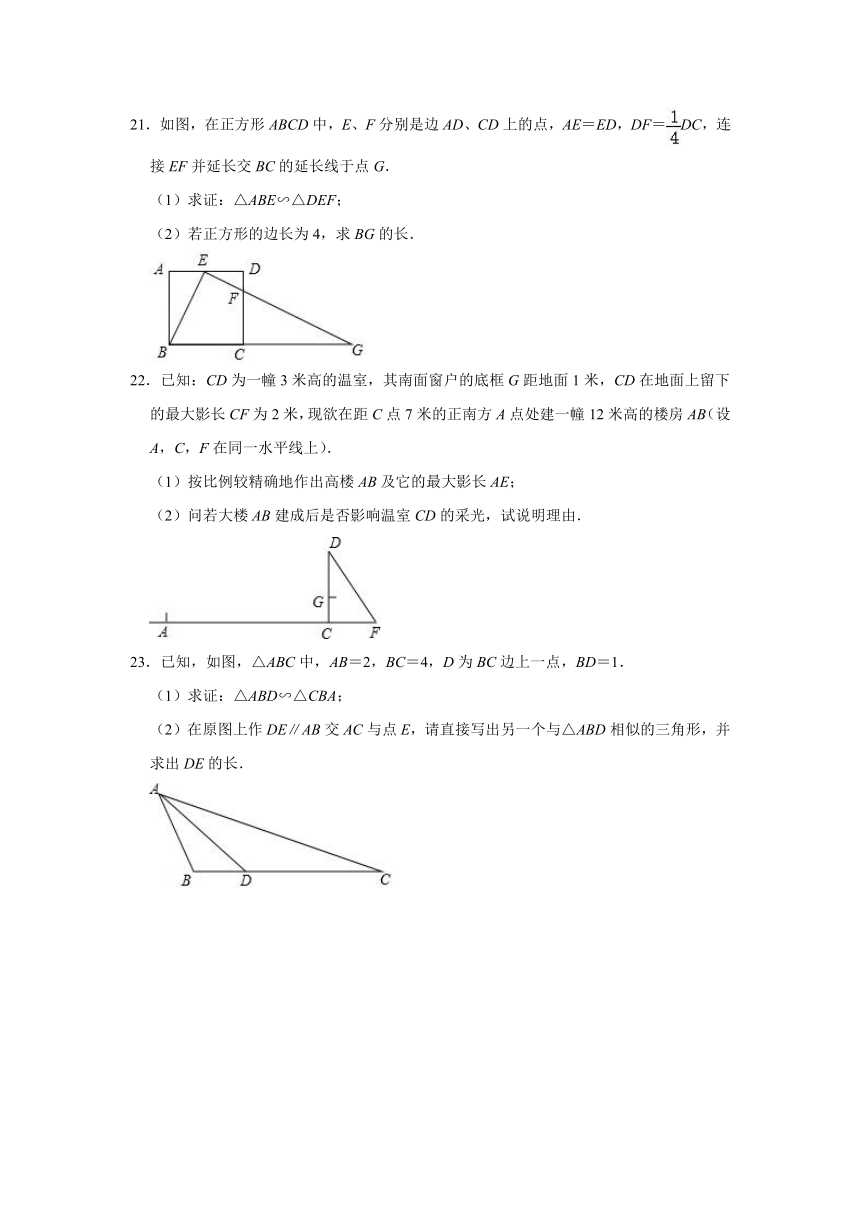
21.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
22.已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(设A,C,F在同一水平线上).
(1)按比例较精确地作出高楼AB及它的最大影长AE;
(2)问若大楼AB建成后是否影响温室CD的采光,试说明理由.
23.已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.
(1)求证:△ABD∽△CBA;
(2)在原图上作DE∥AB交AC与点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:五边形改成与它相似的五边形,如果面积扩大为原来的9倍,
即得到的五边形与原来的五边形的面积的比是9:1,
相似形面积的比等于相似比的平方,
因而相似比是3:1,
相似形周长的比等于相似比,
因而周长扩大为原来的3倍.
故选:B.
2.解:A、两个矩形的角都相等,但对应边的比值不一定相等,因而两个矩形不一定相似;
B、两个梯形,两个平行四边形的角不一定对应相等,边也不一定成比例,因而两个梯形不一定相似,两个平行四边形不一定相似;
C、两个正方形的角都是直角,因而对应角一定相等,并且正方形的边一定相等,因而两个正方形的对应边的比一定相等,即两个正方形一定相似;故正确.
D、两个平行四边形不一定都相似.
故选:C.
3.解:∵两个相似三角形的相似比为1:2,
∴它们面积的比等于()2=.
故选:C.
4.解:∵△ABC∽△DEF,且相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故选:A.
5.解:在△ADC和△BAC中,∠ADC=∠BAC,
如果△ADC∽△BAC,需满足的条件有:
①∠DAC=∠ABC或AC是∠BCD的平分线;
②=;
故选:C.
6.解:∵∠ACP=∠B,∠CAP=∠BAC,
∴△ACP∽△ABC,故选项A正确;
∵∠APC=∠ACB,∠CAP=∠BAC,
∴△ACP∽△ABC,故选项B正确;
∵AC2=AP AB,
∴,
又∵∠CAP=∠BAC,
∴△ACP∽△ABC,故选项C正确;
∵,
但未说明∠ACP=∠ABC,
∴不能判断△ACP∽△ABC,故选项D错误;
故选:D.
7.解:∵BE:EC=2:3,
∴BE:BC=2:5,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴BE:AD=2:5,△ADF∽△EBF,
∴==.
故选:A.
8.解:∵OA=3OC,OB=3OD,
∴OA:OC=OB:OD=3:1,∠AOB=∠DOC,
∴△AOB∽△COD,
∴==,
∴AB=3CD=3×1.8=5.4(cm).
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵两个四边形相似,一个四边形的各边之比为1:2:3:4,
∴和它相似的多边形的对应边的比为1:2:3:4,
∵另一个四边形的最小边长为5cm,
∴最长边为4×5=20cm,
故答案为:20.
10.解:∵两个相似多边形面积比为4:9,
∴两个相似多边形相似比为2:3,
∴两个相似多边形周长比为2:3,
故答案为:2:3.
11.解:∵两个相似三角形的周长之比为2:3,
∴两个相似三角形的相似比是2:3,
∴两个相似三角形的面积比是4:9,
又较小三角形的面积为8cm2,
∴较大三角形的面积为18cm2,
故答案为:18.
12.解:①当△APD∽△PBC时,=,
即=,
解得:PD=1,或PD=4;
②当△PAD∽△PBC时,=,即=,
解得:DP=2.5.
综上所述,DP的长度是1或4或2.5.
故答案是:1或4或2.5.
13.解:∵∠A=∠A,∠AED=∠B,
∴△ADE∽△ACB,
∴AE:AB=AD:AC,
又∵AD=2,DB=4,AE=3,
∴AB=AD+BD=6,
∴AC=2×6÷3=4.
∴CE=AC﹣AE=1.
故答案为:1.
14.解:由题意得,=,
解得h=1.4.
故答案为:1.4.
15.解:
16.解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,
∴CD2=AD BD=8×2,
则CD=4.
故答案是:4.
三.解答题(共7小题,满分40分)
17.(1)证明:∵菱形AEFG∽菱形ABCD,
∴∠EAG=∠BAD,
∴∠EAG+∠GAB=∠BAD+∠GAB,
∴∠EAB=∠GAD,
∵AE=AG,AB=AD,
∴△AEB≌△AGD(SAS),
∴EB=GD;
(2)解:连接BD交AC于点P,则BP⊥AC,
∵∠DAB=60°,
∴∠PAB=30°,
∴BP=AB=1,
AP==,AE=AG=,
∴EP=2,
∴EB===,
∴由(1)知GD=EB=.
18.解:(1)A;
(2)①相似比②相似比的平方③相似比的立方;
(3)由题意知他的体积比为;
又因为体重之比等于体积比,
若设初三时的体重为xkg,
则有=
解得x==60.75.
答:初三时的体重为60.75kg.
19.解:设经x秒钟△PBQ与△ABC相似,
则AP=2xcm,BQ=4xcm,
∵AB=8cm,BC=16cm,
∴BP=AB﹣AP=(8﹣2x)cm,
∵∠B是公共角,
∵①当,即时,△PBQ∽△ABC,
解得:x=2;
②当,即时,△QBP∽△ABC,
解得:x=0.8,
∴经2或0.8秒钟△PBQ与△ABC相似.
20.解:设运动了ts(0<t≤4),根据题意得:AP=2tcm,CQ=3tcm,则AQ=AC﹣CQ=16﹣3t(cm),
当△APQ∽△ABC时,,即,解得:t=;
当△APQ∽△ACB时,,即,解得:t=4;
故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是:s或4s.
21.(1)证明:∵四边形ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴,
∵DF=DC,
∴,
∴,
∴△ABE∽△DEF;
(2)解:∵四边形ABCD为正方形,
∴ED∥BG,
∴,
又∵DF=DC,正方形的边长为4,
∴ED=2,CG=6,
∴BG=BC+CG=10.
22.解:如图,∵HE∥DF,HC∥AB,
∴△CDF∽△ABE∽△CHE,
∴AE:AB=CF:DC,
∴AE=8米,由AC=7米,可得CE=1米,
由比例可知:CH=1.5米>1米,
故影响采光.
23.(1)证明:∵AB=2,BC=4,BD=1,
∴==,
=,
∴=,
∵∠ABD=∠CBA,
∴△ABD∽△CBA;
(2)解:∵DE∥AB,
∴△CDE∽△CBA,
∴△ABD∽△CDE,
∴DE=1.5.
一.选择题(共8小题,满分40分)
1.将一个五边形改成与它相似的五边形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
A.9倍 B.3倍 C.81倍 D.18倍
2.下列说法中,正确的是( )
A.两个矩形相似 B.两个梯形相似
C.两个正方形相似 D.两个平行四边形相似
3.若两个相似三角形的相似比为1:2,则它们面积的比为( )
A.2:1 B.1: C.1:4 D.1:5
4.已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为( )
A.1:4 B.4:1 C.1:2 D.2:1
5.如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
A.∠DAC=∠ABC B.AC是∠BCD的平分线
C.AC2=BC CD D.=
6.如图,已知P是△ABC边AB上的一点,连接CP.以下条件中不能判定△ACP∽△ABC的是( )
A.∠ACP=∠B B.∠APC=∠ACB C.AC2=AP AB D.=
7.如图 ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于( )
A.2:5 B.3:5 C.2:3 D.5:7
8.如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )
A.7.2 cm B.5.4 cm C.3.6 cm D.0.6 cm
二.填空题(共8小题,满分40分)
9.一个四边形的各边之比为1:2:3:4,和它相似的另一个四边形的最小边长为5cm,则它的最大边长为 cm.
10.若两个相似多边形面积比为4:9,则它们的周长比是 .
11.若两个相似三角形的周长之比为2:3,较小三角形的面积为8cm2,则较大三角形面积是 cm2.
12.如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= .
13.如图,△ABC中,∠AED=∠B,AD=2,DB=4,AE=3,则EC= .
14.如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为 米.
15.如图所示,平移方格纸中的图形,使点A平移到A′处,画出放大一倍后的图形.(所画图中线段必须借助直尺画直,并用阴影表示).
16.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为 .
三.解答题(共7小题,满分40分)
17.如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=,求GD的长.
18.阅读下面的短文,并解答下列问题:
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比(a:b).
设S甲、S乙分别表示这两个正方体的表面积,则==()2
又设V甲、V乙分别表示这两个正方体的体积,则==()3
(1)下列几何体中,一定属于相似体的是(A)
A.两个球体B.两个锥体C.两个圆柱体D.两个长方体
(2)请归纳出相似体的三条主要性质:
①相似体的一切对应线段(或弧)长的比等于 ;
②相似体表面积的比等于 ;
③相似体体积比等于 .
(3)假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为1.1米,体重为18千克,到了初三时,身高为1.65米,问他的体重是多少?(不考虑不同时期人体平均密度的变化)
19.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
20.如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
21.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
22.已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(设A,C,F在同一水平线上).
(1)按比例较精确地作出高楼AB及它的最大影长AE;
(2)问若大楼AB建成后是否影响温室CD的采光,试说明理由.
23.已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.
(1)求证:△ABD∽△CBA;
(2)在原图上作DE∥AB交AC与点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:五边形改成与它相似的五边形,如果面积扩大为原来的9倍,
即得到的五边形与原来的五边形的面积的比是9:1,
相似形面积的比等于相似比的平方,
因而相似比是3:1,
相似形周长的比等于相似比,
因而周长扩大为原来的3倍.
故选:B.
2.解:A、两个矩形的角都相等,但对应边的比值不一定相等,因而两个矩形不一定相似;
B、两个梯形,两个平行四边形的角不一定对应相等,边也不一定成比例,因而两个梯形不一定相似,两个平行四边形不一定相似;
C、两个正方形的角都是直角,因而对应角一定相等,并且正方形的边一定相等,因而两个正方形的对应边的比一定相等,即两个正方形一定相似;故正确.
D、两个平行四边形不一定都相似.
故选:C.
3.解:∵两个相似三角形的相似比为1:2,
∴它们面积的比等于()2=.
故选:C.
4.解:∵△ABC∽△DEF,且相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故选:A.
5.解:在△ADC和△BAC中,∠ADC=∠BAC,
如果△ADC∽△BAC,需满足的条件有:
①∠DAC=∠ABC或AC是∠BCD的平分线;
②=;
故选:C.
6.解:∵∠ACP=∠B,∠CAP=∠BAC,
∴△ACP∽△ABC,故选项A正确;
∵∠APC=∠ACB,∠CAP=∠BAC,
∴△ACP∽△ABC,故选项B正确;
∵AC2=AP AB,
∴,
又∵∠CAP=∠BAC,
∴△ACP∽△ABC,故选项C正确;
∵,
但未说明∠ACP=∠ABC,
∴不能判断△ACP∽△ABC,故选项D错误;
故选:D.
7.解:∵BE:EC=2:3,
∴BE:BC=2:5,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴BE:AD=2:5,△ADF∽△EBF,
∴==.
故选:A.
8.解:∵OA=3OC,OB=3OD,
∴OA:OC=OB:OD=3:1,∠AOB=∠DOC,
∴△AOB∽△COD,
∴==,
∴AB=3CD=3×1.8=5.4(cm).
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵两个四边形相似,一个四边形的各边之比为1:2:3:4,
∴和它相似的多边形的对应边的比为1:2:3:4,
∵另一个四边形的最小边长为5cm,
∴最长边为4×5=20cm,
故答案为:20.
10.解:∵两个相似多边形面积比为4:9,
∴两个相似多边形相似比为2:3,
∴两个相似多边形周长比为2:3,
故答案为:2:3.
11.解:∵两个相似三角形的周长之比为2:3,
∴两个相似三角形的相似比是2:3,
∴两个相似三角形的面积比是4:9,
又较小三角形的面积为8cm2,
∴较大三角形的面积为18cm2,
故答案为:18.
12.解:①当△APD∽△PBC时,=,
即=,
解得:PD=1,或PD=4;
②当△PAD∽△PBC时,=,即=,
解得:DP=2.5.
综上所述,DP的长度是1或4或2.5.
故答案是:1或4或2.5.
13.解:∵∠A=∠A,∠AED=∠B,
∴△ADE∽△ACB,
∴AE:AB=AD:AC,
又∵AD=2,DB=4,AE=3,
∴AB=AD+BD=6,
∴AC=2×6÷3=4.
∴CE=AC﹣AE=1.
故答案为:1.
14.解:由题意得,=,
解得h=1.4.
故答案为:1.4.
15.解:
16.解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,
∴CD2=AD BD=8×2,
则CD=4.
故答案是:4.
三.解答题(共7小题,满分40分)
17.(1)证明:∵菱形AEFG∽菱形ABCD,
∴∠EAG=∠BAD,
∴∠EAG+∠GAB=∠BAD+∠GAB,
∴∠EAB=∠GAD,
∵AE=AG,AB=AD,
∴△AEB≌△AGD(SAS),
∴EB=GD;
(2)解:连接BD交AC于点P,则BP⊥AC,
∵∠DAB=60°,
∴∠PAB=30°,
∴BP=AB=1,
AP==,AE=AG=,
∴EP=2,
∴EB===,
∴由(1)知GD=EB=.
18.解:(1)A;
(2)①相似比②相似比的平方③相似比的立方;
(3)由题意知他的体积比为;
又因为体重之比等于体积比,
若设初三时的体重为xkg,
则有=
解得x==60.75.
答:初三时的体重为60.75kg.
19.解:设经x秒钟△PBQ与△ABC相似,
则AP=2xcm,BQ=4xcm,
∵AB=8cm,BC=16cm,
∴BP=AB﹣AP=(8﹣2x)cm,
∵∠B是公共角,
∵①当,即时,△PBQ∽△ABC,
解得:x=2;
②当,即时,△QBP∽△ABC,
解得:x=0.8,
∴经2或0.8秒钟△PBQ与△ABC相似.
20.解:设运动了ts(0<t≤4),根据题意得:AP=2tcm,CQ=3tcm,则AQ=AC﹣CQ=16﹣3t(cm),
当△APQ∽△ABC时,,即,解得:t=;
当△APQ∽△ACB时,,即,解得:t=4;
故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是:s或4s.
21.(1)证明:∵四边形ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴,
∵DF=DC,
∴,
∴,
∴△ABE∽△DEF;
(2)解:∵四边形ABCD为正方形,
∴ED∥BG,
∴,
又∵DF=DC,正方形的边长为4,
∴ED=2,CG=6,
∴BG=BC+CG=10.
22.解:如图,∵HE∥DF,HC∥AB,
∴△CDF∽△ABE∽△CHE,
∴AE:AB=CF:DC,
∴AE=8米,由AC=7米,可得CE=1米,
由比例可知:CH=1.5米>1米,
故影响采光.
23.(1)证明:∵AB=2,BC=4,BD=1,
∴==,
=,
∴=,
∵∠ABD=∠CBA,
∴△ABD∽△CBA;
(2)解:∵DE∥AB,
∴△CDE∽△CBA,
∴△ABD∽△CDE,
∴DE=1.5.
