2021-2022学年人教版九年级数学下册27.2相似三角形 同步达标训练(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2相似三角形 同步达标训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 232.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 09:09:34 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学下册《27.2相似三角形》同步达标训练(附答案)
1.平行四边形ABCD与平行四边形A′B′C′D′相似.已知AB=5,对应边A′B′=6,若平行四边形ABCD的面积为10,则平行四边形A′B′C′D′的面积为( )
A.15 B.14.4 C.12 D.10.8
2.两个相似五边形,一组对应边的长分别为3cm和4.5cm,则这两个多边形的相似比可能是( )
A. B. C. D.
3.如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )
A. B. C. D.2
4.两相似三角形对应高长的比为3:4,则对应中线长的比为( )
A.3:4 B.9:16 C.:2 D.4:3
5.已知:如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
6.已知一个三角形的两个内角分别是30°,70°,另一个三角形的两个内角分别是70°,80°,则这两个三角形( )
A.一定相似 B.不一定相似 C.一定不相似 D.不能确定
7.如图,在正方形ABCD中,F是AD的中点,BF与AC交于点G,则△BGC与四边形CGFD的面积之比是( )
A.1:2 B.2:3 C.3:4 D.4:5
8.如图所示,它是小孔成像的原理,根据图中尺寸(AB∥CD),如果已知物体AB=30,则CD的长应是( )
A.15 B.30 C.20 D.10
9.用一个3倍的放大镜照一个多边形,则放大后的面积是原来的 倍.
10.已知四边形ABCD与四边形A1B1C1D1相似,且AB:BC:CD:DA=20:15:9:8,四边形A1B1C1D1的周长为26,则四边形A1B1C1D1的各边长为 .
11.把一个三角形改做成和它相似的三角形,如果面积扩大到原来的2倍,那么边长应扩大到原来的 倍.
12.已知有两个三角形相似,一个边长分别为2,3,4,另一个的对应边长分别为x,y,12,则x= ,y= .
13.判断下列语句正确的有 .(填写序号)
(1)有一对角相等的三角形一定相似.(2)有一对锐角相等的两个直角三角形一定相似.
(3)有一个角等于100° 的两个等腰三角形相似.(4)有一个角等于30°的两个等腰三角形相似.
(5)有一对角相等的两个等腰三角形一定相似.
14.△ABC和△A1B1C1满足下列条件:
①∠A=68°,∠B=40°,∠A1=68°,∠C1=72°;
②∠A=120°,AB=7,AC=14,∠A1=120°,A1B1=3,A1C1=6;
③AB=4,BC=6,AC=7,A1B1=12,B1C1=18,A1C1=21;
④AB=2,BC=3,∠A=61°,A1B1=4,B1C1=6,∠A=61°.
其中能判定△ABC和△A1B1C1相似的有 .
15.(体验过程题)如图,在平行四边形ABCD中,如果点M为CD的中点,AM与BD相交于点N.
(1)可知△DMN∽ ,则DN:NB= .
(2)S△DMN:S△ANB= ,S△ADN:S△ANB= ,S△DMN:S△ADB= .
(3)S△DMN:S平行四边形ABCD= .
16.如图,小华做物理实验,蜡烛的火焰透过小孔在成像板上形成一个倒立的像,经过测量蜡烛的火焰是2厘米,它的像是4厘米.如果蜡烛距离小圆孔10厘米,那么蜡烛与成像板之间的距离是 .
17.如图,在平面直角坐标系中,已知△ABC,点P(1,2),作△PQR,使△PQR与△ABC相似,以Q、R点必须要格点上 .(不写作法)
18.如图,AB⊥AC,AD⊥BC,已知AB=6,BC=9,则图中线段的长BD= ,AD= ,AC= .
19.图中的两个多边形相似吗?说说你判断的理由.
20.已知四边形ABCD与四边形A′B′C′D′相似,且AB:BC:CD:DA=20:15:9:8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
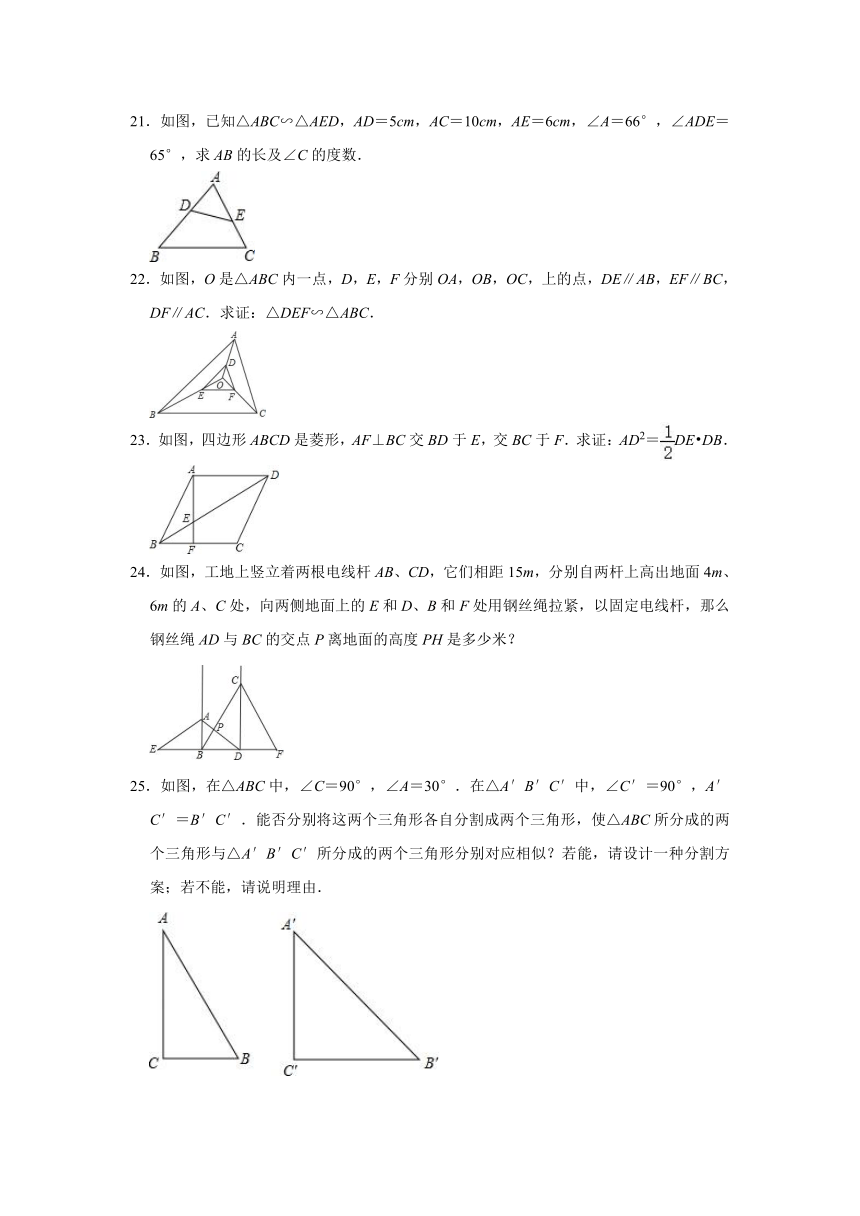
21.如图,已知△ABC∽△AED,AD=5cm,AC=10cm,AE=6cm,∠A=66°,∠ADE=65°,求AB的长及∠C的度数.
22.如图,O是△ABC内一点,D,E,F分别OA,OB,OC,上的点,DE∥AB,EF∥BC,DF∥AC.求证:△DEF∽△ABC.
23.如图,四边形ABCD是菱形,AF⊥BC交BD于E,交BC于F.求证:AD2=DE DB.
24.如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?
25.如图,在△ABC中,∠C=90°,∠A=30°.在△A′B′C′中,∠C′=90°,A′C′=B′C′.能否分别将这两个三角形各自分割成两个三角形,使△ABC所分成的两个三角形与△A′B′C′所分成的两个三角形分别对应相似?若能,请设计一种分割方案;若不能,请说明理由.
参考答案
1.解:平行四边形ABCD与平行四边形A′B′C′D′相似,
AB=5,对应边A′B′=6
则两平行四边形的相似比是5:6,
相似图形面积的等于相似比的平方,
即:平行四边形ABCD的面积:平行四边形A′B′C′D′的面积=25:36,
解得:平行四边形A′B′C′D′的面积为14.4.
故选:B.
2.解:两个多边形的相似比是:=,则相似比可能是.
故选:D.
3.解:∵AD:DB=2:1,
∴=.
∵DE∥BC,
∴△ADE∽△ABC,
∴△ADE与△ABC的相似比==.
故选:B.
4.解:∵两相似三角形对应高长的比为3:4,
∴此两个三角形的相似比为:3:4,
∴对应中线长的比为:3:4.
故选:A.
5.解:∵∠ADE=∠ACD=∠ABC
∴DE∥BC
∴△ADE∽△ABC,
∵DE∥BC
∴∠EDC=∠DCB,
∵∠ACD=∠ABC,
∴△EDC∽△DCB,
同理:∠ACD=∠ABC,∠A=∠A,
∴△ABC∽△ACD,
∵△ADE∽△ABC,△ABC∽△ACD,
∴△ADE∽△ACD
∴共4对
故选:D.
6.解:∵一个三角形的两个内角分别是30°,70°,
∴另一个内角的度数是180°﹣30°﹣70°=80°,
∵70°=70°,80°=80°,
∴这两个三角形一定相似.
故选:A.
7.解:设△AFG的面积为a,
∵点F是AD中点,
∴AF=FD=AD=BC,
∵AD∥BC,
∴△AFG∽△CBG,
∴=()2=,
∴S△BCG=4a,
∵==,
∴=,
∴S△ABG=2a,
则S△ABC=S△BCG+S△ABG=S△ACD=6a,
∴S四边形CGFD=S△ACD﹣S△AFG=5a,
故S△BGC:S四边形CGFD=4a:5a=4:5.
故选:D.
8.解:∵AB∥CD,
∴△AOB∽△COD,
∴36:AB=12:CD,
即36:30=12:CD,
解得CD=10.
故选:D.
9.解:原来的菱形放在3倍的放大镜下,
按照1:3的比例放大,
因此它们是相似多边形,
放大后的面积是原来的9倍.
10.解:四边形ABCD与四边形A1B1C1D1相似,对应边的比相等,
AB:BC:CD:DA=20:15:9:8,
则A1B1:B1C1:C1D1:D1A1=20:15:9:8,
设A1B1=20x,
则B1C1=15x,C1D1=9x,D1A1=8x,
根据四边形A1B1C1D1的周长为26得到:
20x+15x+9x+8x=26,解得x=0.5,
∴四边形A1B1C1D1的各边长为10,7.5,4.5,4.
11.解:因为把一个三角形改做成和它相似的三角形,面积扩大到原来的2倍,所以边长应扩大到原来的倍.
12.解:因为相似三角形对应边成比例,所以,则x=6,y=9.
13.解:(1)有一对角相等的三角形不一定相似.
(2)有一对锐角相等的两个直角三角形一定相似,正确.
(3)有一个角等于100° 的两个等腰三角形相似,正确.
(4)有一个角等于30°的两个等腰三角形不一定相似.
(5)有一对角相等的两个等腰三角形不一定相似.
故答案为:(2)(3)
14.解:①根据三角形内角和定理得到∠C=72°,则在△ABC和△A1B1C1中,∠A=∠A1=68°,∠C=∠C1=72°,所以△ABC和△A1B1C1相似.故①正确;
②根据题意知∠A=120°,∠A1=120°,==,所以△ABC和△A1B1C1相似.故②正确;
③根据题意知:AB:A1B1=BC:B1C1=AC:A1C1=1:3.所以△ABC和△A1B1C1相似.故③正确;
④若∠B=∠B1时,△ABC和△A1B1C1才相似.故④不一定正确;
综上所述,能判定△ABC和△A1B1C1相似的有①②③.
故答案是:①②③.
15.解:(1)∵DC∥AB
∴△DMN∽△BAN
∴DN:NB=DM:AB=1:2
(2)∵DN:NB=DM:AB=1:2
∴S△DMN:S△ANB=1:4
过N作NE⊥AB与E,延长EN交CD与F,则NF:NE=1:2
∵NE,NF分别是△ABN与△DMN的高,S△ADB与S△ANB底边相同,高线的比是3:2
∴S△ADB:S△ANB=3:2
∴S△ADN:S△ANB=1:2
同理:S△DMN:S△ADM=1:3,S△DMN:S△ADB=1:6
(3)S△DMN:S平行四边形ABCD=1:12
16.解:∵AB∥CD,
∴∠A=∠C,∠B=∠D,
∴△AOB∽△COD,
设蜡烛与成像板之间的距离是x厘米.
∴,
解得x=30.
故答案为:30厘米.
17.解:
18.解:∵AB⊥AC,AD⊥BC,
∴AB2=BD BC,即62=BD 9,解得BD=4,
∴CD=BC﹣BD=5,
∵AD2=BD CD,
∴AD==2,
∵AC2=CD BC,
∴AC==3.
故答案为4,2,3.
19.解:不相似.
理由:∵∠D=360°﹣135°﹣95°﹣72°=58°,∠G=360°﹣135°﹣95°﹣59°=71°,
∴两个四边形中不可能有“对应角相等”,
又∵没法判定对应边成比例,
∴不相似.
20.解:∵四边形ABCD与四边形A′B′C′D′相似,
∴A′B′:B′C′:C′D′:D′A′=AB:BC:CD:DA=20:15:9:8
设A′B′=20x,则B′C′=15x,C′D′=9x,D′A′=8x.
∵四边形A′B′C′D′的周长为26,
∴20x+15x+9x+8x=26
解得:x=0.5
∴A′B′=10,B′C′=7.5,C′D′=4.5,D′A′=4.
21.解:∵△ABC∽△AED,∠ADE=65°,
∴∠ADE=∠C=65°,
∵,
∴=,
解得:AB=12cm.
22.解:∵DE∥AB,EF∥BC,DF∥AC,
∴====,
即==,
∴△DEF∽△ABC.
23.证明:连接AC交BD于点O,
∵四边形ABCD为菱形,
∴AC⊥BD,BO=OD,
∵AE⊥AD,
∴△AOD∽△EAD,
∴=,
∴AD2=OD×ED,
即AD2=DE BD.
24.解:作PQ⊥BD于Q,设BQ=x米,QD=y米,PQ=h米,
∵AB∥PQ∥CD,
∴=,=,
即=及=,
∴两式相加得=1,
由此得h=2.4米.
即点P离地面的高度为2.4米.
25.解:如图所示:∵∠C=90°,∠A=30°,∠C′=90°,A′C′=B′C′,
∴∠B=60°,∠A′=∠B′=45°,
又∵∠ACE=∠BCE=45°,∠A′C′F=30°,∠B′C′F=60°,
∴∠A=∠AA′C′F,∠ACE=∠A′,
∴△ACE∽△C′A′F,
∵∠B=∠B′C′F,∠B′=∠BCE,
∴△BCE∽△C′B′F.
1.平行四边形ABCD与平行四边形A′B′C′D′相似.已知AB=5,对应边A′B′=6,若平行四边形ABCD的面积为10,则平行四边形A′B′C′D′的面积为( )
A.15 B.14.4 C.12 D.10.8
2.两个相似五边形,一组对应边的长分别为3cm和4.5cm,则这两个多边形的相似比可能是( )
A. B. C. D.
3.如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )
A. B. C. D.2
4.两相似三角形对应高长的比为3:4,则对应中线长的比为( )
A.3:4 B.9:16 C.:2 D.4:3
5.已知:如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
6.已知一个三角形的两个内角分别是30°,70°,另一个三角形的两个内角分别是70°,80°,则这两个三角形( )
A.一定相似 B.不一定相似 C.一定不相似 D.不能确定
7.如图,在正方形ABCD中,F是AD的中点,BF与AC交于点G,则△BGC与四边形CGFD的面积之比是( )
A.1:2 B.2:3 C.3:4 D.4:5
8.如图所示,它是小孔成像的原理,根据图中尺寸(AB∥CD),如果已知物体AB=30,则CD的长应是( )
A.15 B.30 C.20 D.10
9.用一个3倍的放大镜照一个多边形,则放大后的面积是原来的 倍.
10.已知四边形ABCD与四边形A1B1C1D1相似,且AB:BC:CD:DA=20:15:9:8,四边形A1B1C1D1的周长为26,则四边形A1B1C1D1的各边长为 .
11.把一个三角形改做成和它相似的三角形,如果面积扩大到原来的2倍,那么边长应扩大到原来的 倍.
12.已知有两个三角形相似,一个边长分别为2,3,4,另一个的对应边长分别为x,y,12,则x= ,y= .
13.判断下列语句正确的有 .(填写序号)
(1)有一对角相等的三角形一定相似.(2)有一对锐角相等的两个直角三角形一定相似.
(3)有一个角等于100° 的两个等腰三角形相似.(4)有一个角等于30°的两个等腰三角形相似.
(5)有一对角相等的两个等腰三角形一定相似.
14.△ABC和△A1B1C1满足下列条件:
①∠A=68°,∠B=40°,∠A1=68°,∠C1=72°;
②∠A=120°,AB=7,AC=14,∠A1=120°,A1B1=3,A1C1=6;
③AB=4,BC=6,AC=7,A1B1=12,B1C1=18,A1C1=21;
④AB=2,BC=3,∠A=61°,A1B1=4,B1C1=6,∠A=61°.
其中能判定△ABC和△A1B1C1相似的有 .
15.(体验过程题)如图,在平行四边形ABCD中,如果点M为CD的中点,AM与BD相交于点N.
(1)可知△DMN∽ ,则DN:NB= .
(2)S△DMN:S△ANB= ,S△ADN:S△ANB= ,S△DMN:S△ADB= .
(3)S△DMN:S平行四边形ABCD= .
16.如图,小华做物理实验,蜡烛的火焰透过小孔在成像板上形成一个倒立的像,经过测量蜡烛的火焰是2厘米,它的像是4厘米.如果蜡烛距离小圆孔10厘米,那么蜡烛与成像板之间的距离是 .
17.如图,在平面直角坐标系中,已知△ABC,点P(1,2),作△PQR,使△PQR与△ABC相似,以Q、R点必须要格点上 .(不写作法)
18.如图,AB⊥AC,AD⊥BC,已知AB=6,BC=9,则图中线段的长BD= ,AD= ,AC= .
19.图中的两个多边形相似吗?说说你判断的理由.
20.已知四边形ABCD与四边形A′B′C′D′相似,且AB:BC:CD:DA=20:15:9:8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
21.如图,已知△ABC∽△AED,AD=5cm,AC=10cm,AE=6cm,∠A=66°,∠ADE=65°,求AB的长及∠C的度数.
22.如图,O是△ABC内一点,D,E,F分别OA,OB,OC,上的点,DE∥AB,EF∥BC,DF∥AC.求证:△DEF∽△ABC.
23.如图,四边形ABCD是菱形,AF⊥BC交BD于E,交BC于F.求证:AD2=DE DB.
24.如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?
25.如图,在△ABC中,∠C=90°,∠A=30°.在△A′B′C′中,∠C′=90°,A′C′=B′C′.能否分别将这两个三角形各自分割成两个三角形,使△ABC所分成的两个三角形与△A′B′C′所分成的两个三角形分别对应相似?若能,请设计一种分割方案;若不能,请说明理由.
参考答案
1.解:平行四边形ABCD与平行四边形A′B′C′D′相似,
AB=5,对应边A′B′=6
则两平行四边形的相似比是5:6,
相似图形面积的等于相似比的平方,
即:平行四边形ABCD的面积:平行四边形A′B′C′D′的面积=25:36,
解得:平行四边形A′B′C′D′的面积为14.4.
故选:B.
2.解:两个多边形的相似比是:=,则相似比可能是.
故选:D.
3.解:∵AD:DB=2:1,
∴=.
∵DE∥BC,
∴△ADE∽△ABC,
∴△ADE与△ABC的相似比==.
故选:B.
4.解:∵两相似三角形对应高长的比为3:4,
∴此两个三角形的相似比为:3:4,
∴对应中线长的比为:3:4.
故选:A.
5.解:∵∠ADE=∠ACD=∠ABC
∴DE∥BC
∴△ADE∽△ABC,
∵DE∥BC
∴∠EDC=∠DCB,
∵∠ACD=∠ABC,
∴△EDC∽△DCB,
同理:∠ACD=∠ABC,∠A=∠A,
∴△ABC∽△ACD,
∵△ADE∽△ABC,△ABC∽△ACD,
∴△ADE∽△ACD
∴共4对
故选:D.
6.解:∵一个三角形的两个内角分别是30°,70°,
∴另一个内角的度数是180°﹣30°﹣70°=80°,
∵70°=70°,80°=80°,
∴这两个三角形一定相似.
故选:A.
7.解:设△AFG的面积为a,
∵点F是AD中点,
∴AF=FD=AD=BC,
∵AD∥BC,
∴△AFG∽△CBG,
∴=()2=,
∴S△BCG=4a,
∵==,
∴=,
∴S△ABG=2a,
则S△ABC=S△BCG+S△ABG=S△ACD=6a,
∴S四边形CGFD=S△ACD﹣S△AFG=5a,
故S△BGC:S四边形CGFD=4a:5a=4:5.
故选:D.
8.解:∵AB∥CD,
∴△AOB∽△COD,
∴36:AB=12:CD,
即36:30=12:CD,
解得CD=10.
故选:D.
9.解:原来的菱形放在3倍的放大镜下,
按照1:3的比例放大,
因此它们是相似多边形,
放大后的面积是原来的9倍.
10.解:四边形ABCD与四边形A1B1C1D1相似,对应边的比相等,
AB:BC:CD:DA=20:15:9:8,
则A1B1:B1C1:C1D1:D1A1=20:15:9:8,
设A1B1=20x,
则B1C1=15x,C1D1=9x,D1A1=8x,
根据四边形A1B1C1D1的周长为26得到:
20x+15x+9x+8x=26,解得x=0.5,
∴四边形A1B1C1D1的各边长为10,7.5,4.5,4.
11.解:因为把一个三角形改做成和它相似的三角形,面积扩大到原来的2倍,所以边长应扩大到原来的倍.
12.解:因为相似三角形对应边成比例,所以,则x=6,y=9.
13.解:(1)有一对角相等的三角形不一定相似.
(2)有一对锐角相等的两个直角三角形一定相似,正确.
(3)有一个角等于100° 的两个等腰三角形相似,正确.
(4)有一个角等于30°的两个等腰三角形不一定相似.
(5)有一对角相等的两个等腰三角形不一定相似.
故答案为:(2)(3)
14.解:①根据三角形内角和定理得到∠C=72°,则在△ABC和△A1B1C1中,∠A=∠A1=68°,∠C=∠C1=72°,所以△ABC和△A1B1C1相似.故①正确;
②根据题意知∠A=120°,∠A1=120°,==,所以△ABC和△A1B1C1相似.故②正确;
③根据题意知:AB:A1B1=BC:B1C1=AC:A1C1=1:3.所以△ABC和△A1B1C1相似.故③正确;
④若∠B=∠B1时,△ABC和△A1B1C1才相似.故④不一定正确;
综上所述,能判定△ABC和△A1B1C1相似的有①②③.
故答案是:①②③.
15.解:(1)∵DC∥AB
∴△DMN∽△BAN
∴DN:NB=DM:AB=1:2
(2)∵DN:NB=DM:AB=1:2
∴S△DMN:S△ANB=1:4
过N作NE⊥AB与E,延长EN交CD与F,则NF:NE=1:2
∵NE,NF分别是△ABN与△DMN的高,S△ADB与S△ANB底边相同,高线的比是3:2
∴S△ADB:S△ANB=3:2
∴S△ADN:S△ANB=1:2
同理:S△DMN:S△ADM=1:3,S△DMN:S△ADB=1:6
(3)S△DMN:S平行四边形ABCD=1:12
16.解:∵AB∥CD,
∴∠A=∠C,∠B=∠D,
∴△AOB∽△COD,
设蜡烛与成像板之间的距离是x厘米.
∴,
解得x=30.
故答案为:30厘米.
17.解:
18.解:∵AB⊥AC,AD⊥BC,
∴AB2=BD BC,即62=BD 9,解得BD=4,
∴CD=BC﹣BD=5,
∵AD2=BD CD,
∴AD==2,
∵AC2=CD BC,
∴AC==3.
故答案为4,2,3.
19.解:不相似.
理由:∵∠D=360°﹣135°﹣95°﹣72°=58°,∠G=360°﹣135°﹣95°﹣59°=71°,
∴两个四边形中不可能有“对应角相等”,
又∵没法判定对应边成比例,
∴不相似.
20.解:∵四边形ABCD与四边形A′B′C′D′相似,
∴A′B′:B′C′:C′D′:D′A′=AB:BC:CD:DA=20:15:9:8
设A′B′=20x,则B′C′=15x,C′D′=9x,D′A′=8x.
∵四边形A′B′C′D′的周长为26,
∴20x+15x+9x+8x=26
解得:x=0.5
∴A′B′=10,B′C′=7.5,C′D′=4.5,D′A′=4.
21.解:∵△ABC∽△AED,∠ADE=65°,
∴∠ADE=∠C=65°,
∵,
∴=,
解得:AB=12cm.
22.解:∵DE∥AB,EF∥BC,DF∥AC,
∴====,
即==,
∴△DEF∽△ABC.
23.证明:连接AC交BD于点O,
∵四边形ABCD为菱形,
∴AC⊥BD,BO=OD,
∵AE⊥AD,
∴△AOD∽△EAD,
∴=,
∴AD2=OD×ED,
即AD2=DE BD.
24.解:作PQ⊥BD于Q,设BQ=x米,QD=y米,PQ=h米,
∵AB∥PQ∥CD,
∴=,=,
即=及=,
∴两式相加得=1,
由此得h=2.4米.
即点P离地面的高度为2.4米.
25.解:如图所示:∵∠C=90°,∠A=30°,∠C′=90°,A′C′=B′C′,
∴∠B=60°,∠A′=∠B′=45°,
又∵∠ACE=∠BCE=45°,∠A′C′F=30°,∠B′C′F=60°,
∴∠A=∠AA′C′F,∠ACE=∠A′,
∴△ACE∽△C′A′F,
∵∠B=∠B′C′F,∠B′=∠BCE,
∴△BCE∽△C′B′F.
