2021-2022学年人教版九年级数学下册27.2相似三角形同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2相似三角形同步练习题(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 294.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览


文档简介
2021-2022学年人教版九年级数学下册《27.2相似三角形》同步练习题(附答案)
1.若四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,AB=8cm,A′B′=6cm,AD=5cm,则A′D′等于( )
A.cm B.cm C.cm D.cm
2.如图,为了测量某棵树的高度,小刚用长为2m的竹竿作测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距6m,与树距15m,那么这颗树的高度为( )
A.5m B.7m C.7.5m D.21m
3.如图△ABC中,∠ACB=90°,CD⊥AB于D,若AC=2,AB=3,则CD为( )
A. B. C.2 D.3
4.如果五边形ABCDE∽五边形POGMN且对应高之比为3:2,那么五边形ABCDE和五边形POGMN的面积之比是( )
A.2:3 B.3:2 C.6:4 D.9:4
5.如图,已知矩形ABCD中,AB=3,BE=2,EF⊥BC.若四边形EFDC与四边形BEFA相似而不全等,则CE=( )
A.3 B.3.5 C.4 D.4.5
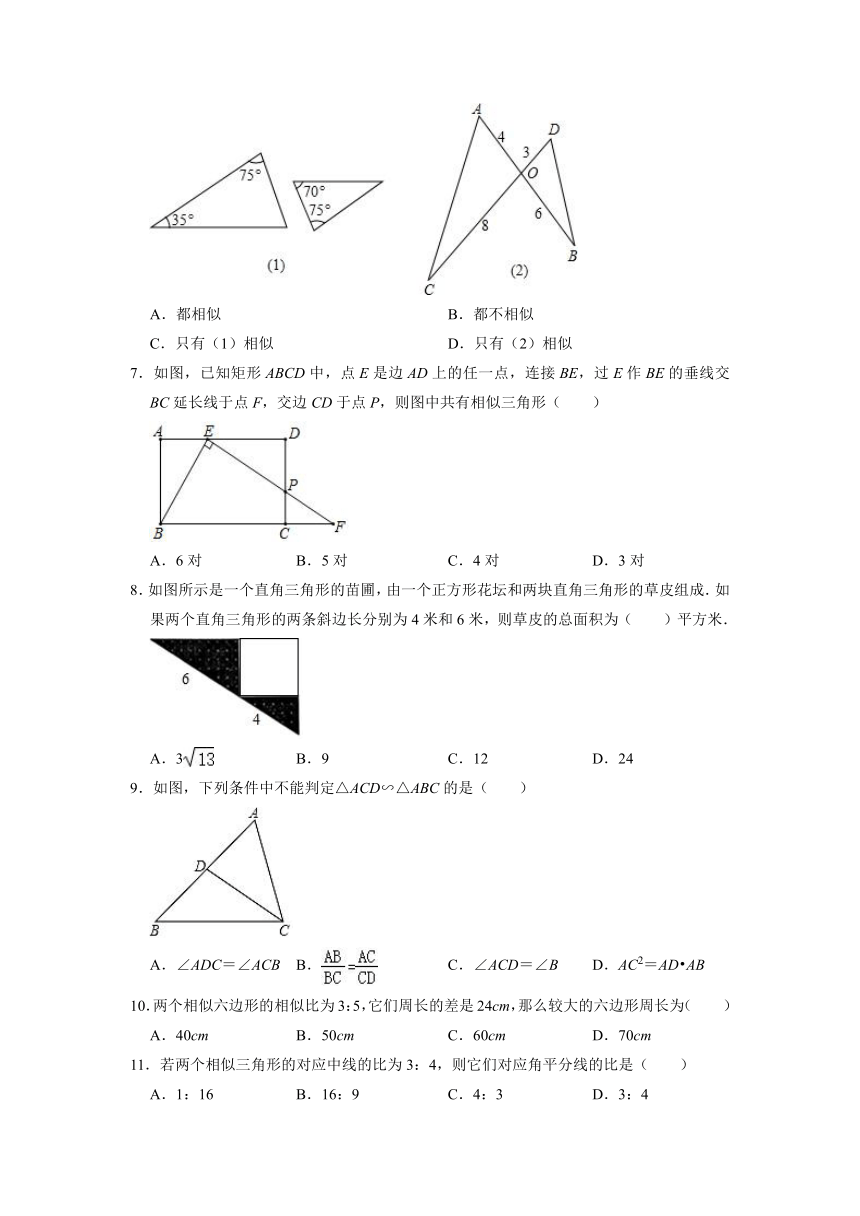
6.已知如图(1)、(2)中各有两个三角形,其边长和角的度数如图上标注,则对图(1)、(2)中的两个三角形,下列说法正确的是( )
A.都相似 B.都不相似
C.只有(1)相似 D.只有(2)相似
7.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对 B.5对 C.4对 D.3对
8.如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
A.3 B.9 C.12 D.24
9.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B. C.∠ACD=∠B D.AC2=AD AB
10.两个相似六边形的相似比为3:5,它们周长的差是24cm,那么较大的六边形周长为( )
A.40cm B.50cm C.60cm D.70cm
11.若两个相似三角形的对应中线的比为3:4,则它们对应角平分线的比是( )
A.1:16 B.16:9 C.4:3 D.3:4
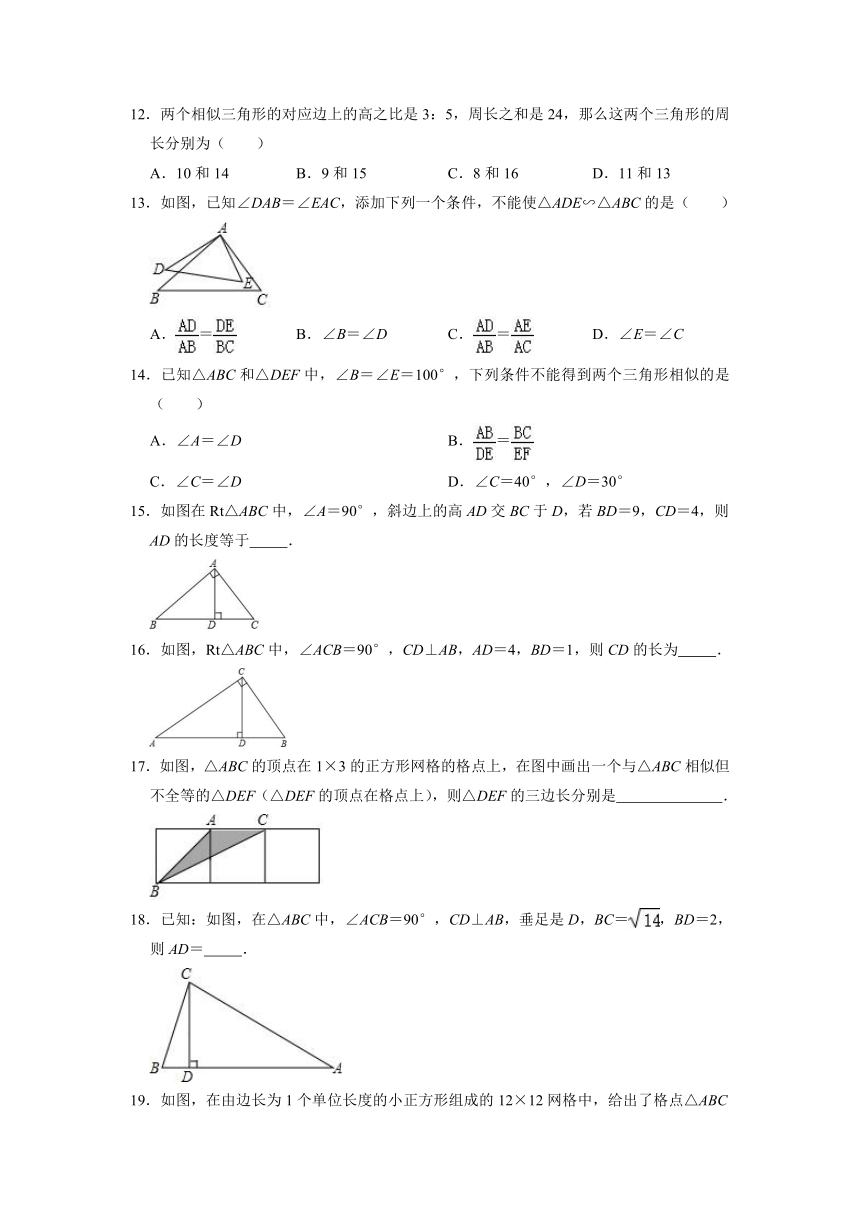
12.两个相似三角形的对应边上的高之比是3:5,周长之和是24,那么这两个三角形的周长分别为( )
A.10和14 B.9和15 C.8和16 D.11和13
13.如图,已知∠DAB=∠EAC,添加下列一个条件,不能使△ADE∽△ABC的是( )
A.= B.∠B=∠D C.= D.∠E=∠C
14.已知△ABC和△DEF中,∠B=∠E=100°,下列条件不能得到两个三角形相似的是( )
A.∠A=∠D B.=
C.∠C=∠D D.∠C=40°,∠D=30°
15.如图在Rt△ABC中,∠A=90°,斜边上的高AD交BC于D,若BD=9,CD=4,则AD的长度等于 .
16.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AD=4,BD=1,则CD的长为 .
17.如图,△ABC的顶点在1×3的正方形网格的格点上,在图中画出一个与△ABC相似但不全等的△DEF(△DEF的顶点在格点上),则△DEF的三边长分别是 .
18.已知:如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,BC=,BD=2,则AD= .
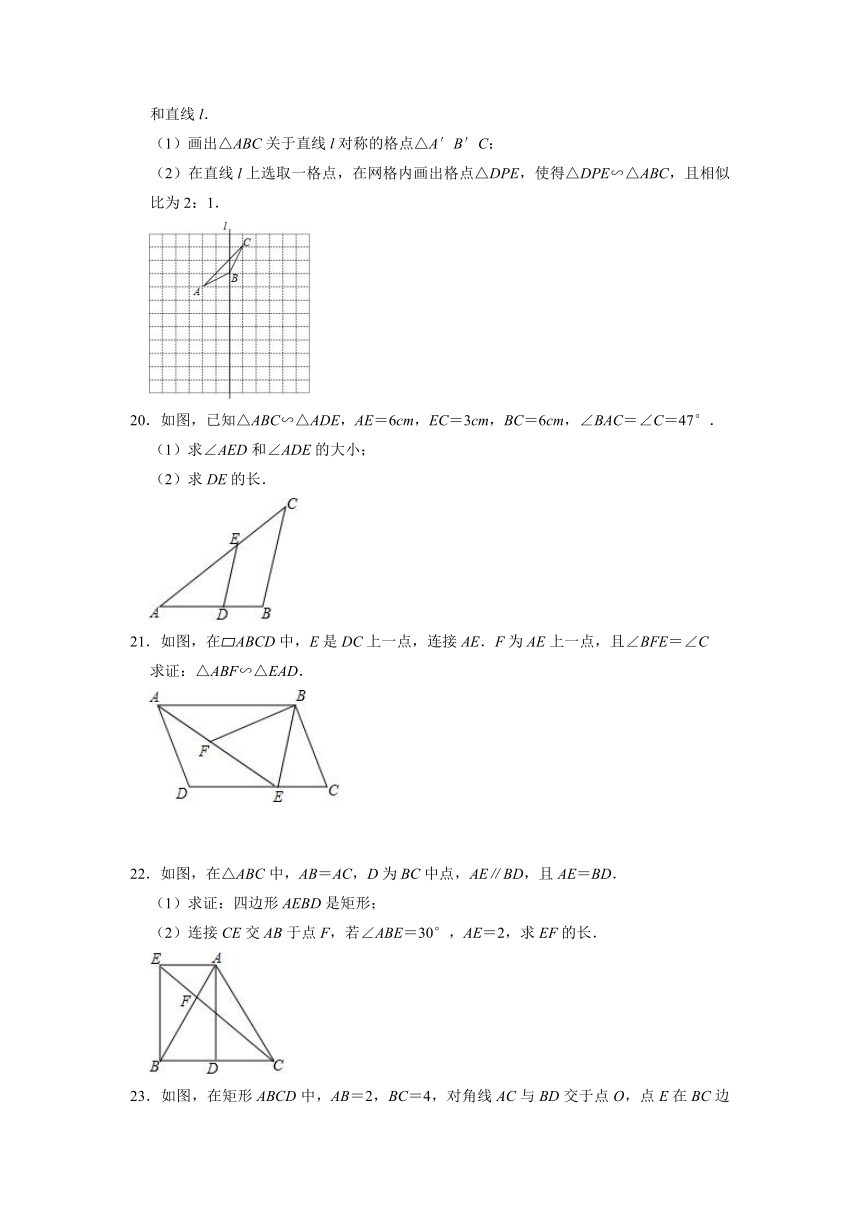
19.如图,在由边长为1个单位长度的小正方形组成的12×12网格中,给出了格点△ABC和直线l.
(1)画出△ABC关于直线l对称的格点△A′B′C;
(2)在直线l上选取一格点,在网格内画出格点△DPE,使得△DPE∽△ABC,且相似比为2:1.
20.如图,已知△ABC∽△ADE,AE=6cm,EC=3cm,BC=6cm,∠BAC=∠C=47°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长.
21.如图,在 ABCD中,E是DC上一点,连接AE.F为AE上一点,且∠BFE=∠C
求证:△ABF∽△EAD.
22.如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.
23.如图,在矩形ABCD中,AB=2,BC=4,对角线AC与BD交于点O,点E在BC边上,DE与AC交于点F,∠CDE=∠CBD.
求:(1)CE的长;
(2)EF的长.
24.如图, ABCD中,E是AB中点,AC与DE交于点F.
(1)求证:△DFC∽△EFA.
(2)若AC⊥DE,AB=2,AF=2,求DF长.
参考答案
1.解:∵四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,
∴=,
∵AB=8cm,A′B′=6cm,AD=5cm,
∴=,
则A′D′=.
故选:B.
2.解:如图,
∵AB⊥OD,CD⊥OD,
∴AB∥CD,
∴△OAB∽△OCD,
∴=,
∵AB=2m,OB=6m,OD=6+15=21m,
∴=,
解得CD=7m.
这颗树的高度为7m,
故选:B.
3.解:根据题意得:BC===.
∵△ABC的面积= AC BC= AB CD
∴CD===2.
故选:C.
4.解:∵五边形ABCDE∽五边形POGMN且对应高之比为3:2,
∴相似比为3:2,
∴五边形ABCDE和五边形FGHIJ的面积比是9:4,
故选:D.
5.解:设CE=x,
∵四边形EFDC与四边形BEFA相似,
∴,
∵AB=3,BE=2,EF=AB,
∴,
解得:x=4.5,
故选:D.
6.解:在图(1)中,∠C=180°﹣∠A﹣∠B=180°﹣75°﹣35°=70°,
则∠A=∠D,∠C=∠E,
∴△ABC∽△DFE;
在图(2)中,=,==,
∴=,又∠AOC=∠DOB,
∴△AOC∽△DOB,
故选:A.
7.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=∠DCB=90°,
∴∠PCF=90°,
∵BE⊥EF,
∴∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠DEP=90°,
∴∠ABE=∠DEP,
∵AD∥BC,
∴∠DEP=∠F,
∴∠ABE=∠DEP=∠F,
∴△ABE∽△DEP∽△EFB∽△CFP,
∴图中共有相似三角形有6对,
故选:A.
8.解:∵△MDE是直角三角形,四边形ABCD是正方形,
∴∠MAB=∠BCE=90°,∠M+∠ABM=90°,∠ABM+∠CBE=90°,
∴∠M=∠CBE,
∴△AMB∽△CBE,
∴=,
∵MB=6,BE=4,
∴===,
∵AB=BC,
∴=,
设CE=2x,则BC=3x,在Rt△CBE中,
BE2=BC2+CE2,即42=(3x)2+(2x)2,解得x=,
∴CE=,AB=BC=,AM=AB=,
∴S草皮=S△CBE+S△AMB=××+××
=12.
故选:C.
9.解:A、由∠ADC=∠ACB,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
B、由不能判定△ACD∽△ABC,此选项符合题意;
C、由∠ACD=∠B,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
D、由AC2=AD AB,即=,且∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
故选:B.
10.解:由题意,可设较小多边形的周长为3x,则较大多边形的周长为5x,
则有:5x﹣3x=24,
解得x=12,
∴5x=60,
故选:C.
11.解:∵两个相似三角形对应中线的比是3:4,
∴这两个相似三角形的相似比是3:4,
那么它们的对应角平分线的比为3:4,
故选:D.
12.解:∵两个相似三角形的对应边上的高之比是3:5,
∴这两个三角形周长比为:3:5,
∵周长之和是24,
∴这两个三角形周长分别为:24×=9,24×=15.
故选:B.
13.解:∵∠DAB=∠CAE,
∴∠DAB+∠BAE=∠CAE+∠BAE,
即∠DAE=∠BAC,
∴∠B=∠D或∠E=∠C或,
∴△ADE∽△ABC,
故选:A.
14.解:在△ABC和△DEF中,∠B=∠E=100°,
A、当∠A=∠D时,△ABC∽△DEF,故能判定这两个三角形相似;
B、当时,△ABC∽△DEF,故能判定这两个三角形相似;
C、当∠C=∠D时,△ABC∽△DEF,故能判定这两个三角形相似;
D、当∠C=40°,∠D=30°时,不能判断这两个三角形相似.
故选:D.
15.解:由射影定理得,AD2=BD CD,
则AD2=9×4=36,
∴AD=6,
故答案为:6.
16.解:∵如图,在Rt△ABC中,∠C=90°,CD⊥AB,AD=4,BD=1,
∴由射影定理得:CD2=BD AD=1×4=4,
∴CD=2(舍去负值).
故答案是:2.
17.解:如图所示:△ABC∽△DEF,
DE=,ED=2,EF=.
故答案为:,2,.
18.解:由射影定理得,BC2=BD BA,
则BA=7,
∴AD=BA﹣BD=5,
故答案为:5
19.解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:△DPE即为所求.
20.解:(1)∵△ABC∽△ADE,
∴∠AED=∠C=47°,
∠ADE=180°﹣∠BAC﹣∠AED=86°;
(2)∵△ABC∽△ADE,
∴=,即=,
解得,DE=4(cm).
21.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD∥BC,
∴∠D+∠C=180°.
∵∠AFB+∠BFE=180°且∠BFE=∠C.
∴∠D=∠AFB.
∵AB∥CD,
∴∠BAE=∠AED,
∴△ABF∽△EAD.
22.(1)证明:∵AE∥BD,AE=BD,
∴四边形AEBD是平行四边形,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形.
(2)解:∵四边形AEBD是矩形,
∴∠AEB=90°,
∵∠ABE=30°,AE=2,
∴BE=2,BC=4,
∴EC=2,
∵AE∥BC,
∴△AEF∽△BCF,
∴==,
∴EF=EC=.
23.解:(1)∵四边形ABCD是矩形,AB=2,BC=4,
∴AD∥BC,CD=AB=2,
∴∠ADB=∠CBD,
∵∠EDC=∠ADB,
∴∠EDC=∠CBD,
∵∠ECD=∠DCB,
∴△CDE∽△CBD,
∴CE:CD=CD:CB,
∴CE:2=2:4,
解得:CE=1;
(2)∵AD∥BC,
∴△ADF∽△CEF,
∴DF:EF=AD:CE=4:1,
∴EF:DE=1:5,
∵∠DCB=90°,
∴DE==,
∴EF=.
24.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,AB=CD,
∴△DFC∽△EFA;
(2)解:∵E是AB中点,
∴AE=AB=,
∵AC⊥DE,
∴∠AFE=90°,
∴FE==1,
∵△DFC∽△EFA,
∴==,
∴DF=2EF=2.
1.若四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,AB=8cm,A′B′=6cm,AD=5cm,则A′D′等于( )
A.cm B.cm C.cm D.cm
2.如图,为了测量某棵树的高度,小刚用长为2m的竹竿作测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距6m,与树距15m,那么这颗树的高度为( )
A.5m B.7m C.7.5m D.21m
3.如图△ABC中,∠ACB=90°,CD⊥AB于D,若AC=2,AB=3,则CD为( )
A. B. C.2 D.3
4.如果五边形ABCDE∽五边形POGMN且对应高之比为3:2,那么五边形ABCDE和五边形POGMN的面积之比是( )
A.2:3 B.3:2 C.6:4 D.9:4
5.如图,已知矩形ABCD中,AB=3,BE=2,EF⊥BC.若四边形EFDC与四边形BEFA相似而不全等,则CE=( )
A.3 B.3.5 C.4 D.4.5
6.已知如图(1)、(2)中各有两个三角形,其边长和角的度数如图上标注,则对图(1)、(2)中的两个三角形,下列说法正确的是( )
A.都相似 B.都不相似
C.只有(1)相似 D.只有(2)相似
7.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对 B.5对 C.4对 D.3对
8.如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
A.3 B.9 C.12 D.24
9.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B. C.∠ACD=∠B D.AC2=AD AB
10.两个相似六边形的相似比为3:5,它们周长的差是24cm,那么较大的六边形周长为( )
A.40cm B.50cm C.60cm D.70cm
11.若两个相似三角形的对应中线的比为3:4,则它们对应角平分线的比是( )
A.1:16 B.16:9 C.4:3 D.3:4
12.两个相似三角形的对应边上的高之比是3:5,周长之和是24,那么这两个三角形的周长分别为( )
A.10和14 B.9和15 C.8和16 D.11和13
13.如图,已知∠DAB=∠EAC,添加下列一个条件,不能使△ADE∽△ABC的是( )
A.= B.∠B=∠D C.= D.∠E=∠C
14.已知△ABC和△DEF中,∠B=∠E=100°,下列条件不能得到两个三角形相似的是( )
A.∠A=∠D B.=
C.∠C=∠D D.∠C=40°,∠D=30°
15.如图在Rt△ABC中,∠A=90°,斜边上的高AD交BC于D,若BD=9,CD=4,则AD的长度等于 .
16.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AD=4,BD=1,则CD的长为 .
17.如图,△ABC的顶点在1×3的正方形网格的格点上,在图中画出一个与△ABC相似但不全等的△DEF(△DEF的顶点在格点上),则△DEF的三边长分别是 .
18.已知:如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,BC=,BD=2,则AD= .
19.如图,在由边长为1个单位长度的小正方形组成的12×12网格中,给出了格点△ABC和直线l.
(1)画出△ABC关于直线l对称的格点△A′B′C;
(2)在直线l上选取一格点,在网格内画出格点△DPE,使得△DPE∽△ABC,且相似比为2:1.
20.如图,已知△ABC∽△ADE,AE=6cm,EC=3cm,BC=6cm,∠BAC=∠C=47°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长.
21.如图,在 ABCD中,E是DC上一点,连接AE.F为AE上一点,且∠BFE=∠C
求证:△ABF∽△EAD.
22.如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.
23.如图,在矩形ABCD中,AB=2,BC=4,对角线AC与BD交于点O,点E在BC边上,DE与AC交于点F,∠CDE=∠CBD.
求:(1)CE的长;
(2)EF的长.
24.如图, ABCD中,E是AB中点,AC与DE交于点F.
(1)求证:△DFC∽△EFA.
(2)若AC⊥DE,AB=2,AF=2,求DF长.
参考答案
1.解:∵四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,
∴=,
∵AB=8cm,A′B′=6cm,AD=5cm,
∴=,
则A′D′=.
故选:B.
2.解:如图,
∵AB⊥OD,CD⊥OD,
∴AB∥CD,
∴△OAB∽△OCD,
∴=,
∵AB=2m,OB=6m,OD=6+15=21m,
∴=,
解得CD=7m.
这颗树的高度为7m,
故选:B.
3.解:根据题意得:BC===.
∵△ABC的面积= AC BC= AB CD
∴CD===2.
故选:C.
4.解:∵五边形ABCDE∽五边形POGMN且对应高之比为3:2,
∴相似比为3:2,
∴五边形ABCDE和五边形FGHIJ的面积比是9:4,
故选:D.
5.解:设CE=x,
∵四边形EFDC与四边形BEFA相似,
∴,
∵AB=3,BE=2,EF=AB,
∴,
解得:x=4.5,
故选:D.
6.解:在图(1)中,∠C=180°﹣∠A﹣∠B=180°﹣75°﹣35°=70°,
则∠A=∠D,∠C=∠E,
∴△ABC∽△DFE;
在图(2)中,=,==,
∴=,又∠AOC=∠DOB,
∴△AOC∽△DOB,
故选:A.
7.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=∠DCB=90°,
∴∠PCF=90°,
∵BE⊥EF,
∴∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠DEP=90°,
∴∠ABE=∠DEP,
∵AD∥BC,
∴∠DEP=∠F,
∴∠ABE=∠DEP=∠F,
∴△ABE∽△DEP∽△EFB∽△CFP,
∴图中共有相似三角形有6对,
故选:A.
8.解:∵△MDE是直角三角形,四边形ABCD是正方形,
∴∠MAB=∠BCE=90°,∠M+∠ABM=90°,∠ABM+∠CBE=90°,
∴∠M=∠CBE,
∴△AMB∽△CBE,
∴=,
∵MB=6,BE=4,
∴===,
∵AB=BC,
∴=,
设CE=2x,则BC=3x,在Rt△CBE中,
BE2=BC2+CE2,即42=(3x)2+(2x)2,解得x=,
∴CE=,AB=BC=,AM=AB=,
∴S草皮=S△CBE+S△AMB=××+××
=12.
故选:C.
9.解:A、由∠ADC=∠ACB,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
B、由不能判定△ACD∽△ABC,此选项符合题意;
C、由∠ACD=∠B,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
D、由AC2=AD AB,即=,且∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
故选:B.
10.解:由题意,可设较小多边形的周长为3x,则较大多边形的周长为5x,
则有:5x﹣3x=24,
解得x=12,
∴5x=60,
故选:C.
11.解:∵两个相似三角形对应中线的比是3:4,
∴这两个相似三角形的相似比是3:4,
那么它们的对应角平分线的比为3:4,
故选:D.
12.解:∵两个相似三角形的对应边上的高之比是3:5,
∴这两个三角形周长比为:3:5,
∵周长之和是24,
∴这两个三角形周长分别为:24×=9,24×=15.
故选:B.
13.解:∵∠DAB=∠CAE,
∴∠DAB+∠BAE=∠CAE+∠BAE,
即∠DAE=∠BAC,
∴∠B=∠D或∠E=∠C或,
∴△ADE∽△ABC,
故选:A.
14.解:在△ABC和△DEF中,∠B=∠E=100°,
A、当∠A=∠D时,△ABC∽△DEF,故能判定这两个三角形相似;
B、当时,△ABC∽△DEF,故能判定这两个三角形相似;
C、当∠C=∠D时,△ABC∽△DEF,故能判定这两个三角形相似;
D、当∠C=40°,∠D=30°时,不能判断这两个三角形相似.
故选:D.
15.解:由射影定理得,AD2=BD CD,
则AD2=9×4=36,
∴AD=6,
故答案为:6.
16.解:∵如图,在Rt△ABC中,∠C=90°,CD⊥AB,AD=4,BD=1,
∴由射影定理得:CD2=BD AD=1×4=4,
∴CD=2(舍去负值).
故答案是:2.
17.解:如图所示:△ABC∽△DEF,
DE=,ED=2,EF=.
故答案为:,2,.
18.解:由射影定理得,BC2=BD BA,
则BA=7,
∴AD=BA﹣BD=5,
故答案为:5
19.解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:△DPE即为所求.
20.解:(1)∵△ABC∽△ADE,
∴∠AED=∠C=47°,
∠ADE=180°﹣∠BAC﹣∠AED=86°;
(2)∵△ABC∽△ADE,
∴=,即=,
解得,DE=4(cm).
21.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD∥BC,
∴∠D+∠C=180°.
∵∠AFB+∠BFE=180°且∠BFE=∠C.
∴∠D=∠AFB.
∵AB∥CD,
∴∠BAE=∠AED,
∴△ABF∽△EAD.
22.(1)证明:∵AE∥BD,AE=BD,
∴四边形AEBD是平行四边形,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形.
(2)解:∵四边形AEBD是矩形,
∴∠AEB=90°,
∵∠ABE=30°,AE=2,
∴BE=2,BC=4,
∴EC=2,
∵AE∥BC,
∴△AEF∽△BCF,
∴==,
∴EF=EC=.
23.解:(1)∵四边形ABCD是矩形,AB=2,BC=4,
∴AD∥BC,CD=AB=2,
∴∠ADB=∠CBD,
∵∠EDC=∠ADB,
∴∠EDC=∠CBD,
∵∠ECD=∠DCB,
∴△CDE∽△CBD,
∴CE:CD=CD:CB,
∴CE:2=2:4,
解得:CE=1;
(2)∵AD∥BC,
∴△ADF∽△CEF,
∴DF:EF=AD:CE=4:1,
∴EF:DE=1:5,
∵∠DCB=90°,
∴DE==,
∴EF=.
24.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,AB=CD,
∴△DFC∽△EFA;
(2)解:∵E是AB中点,
∴AE=AB=,
∵AC⊥DE,
∴∠AFE=90°,
∴FE==1,
∵△DFC∽△EFA,
∴==,
∴DF=2EF=2.
