[原创]2013年《随堂优化训练》数学28.2 锐角三角函数
文档属性
| 名称 | [原创]2013年《随堂优化训练》数学28.2 锐角三角函数 |  | |
| 格式 | zip | ||
| 文件大小 | 356.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-07 09:07:20 | ||
图片预览



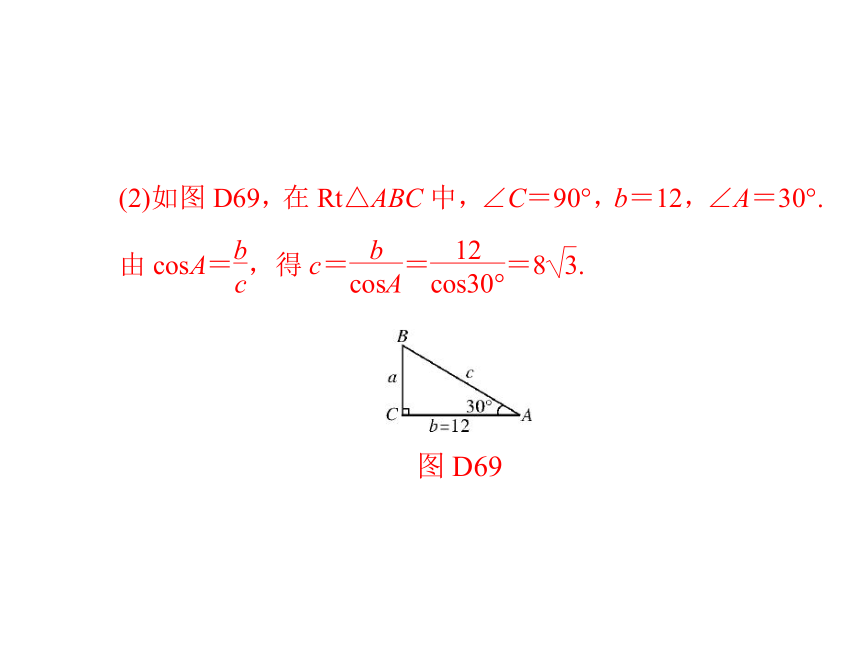
文档简介
(共21张PPT)
28.2
解直角三角形
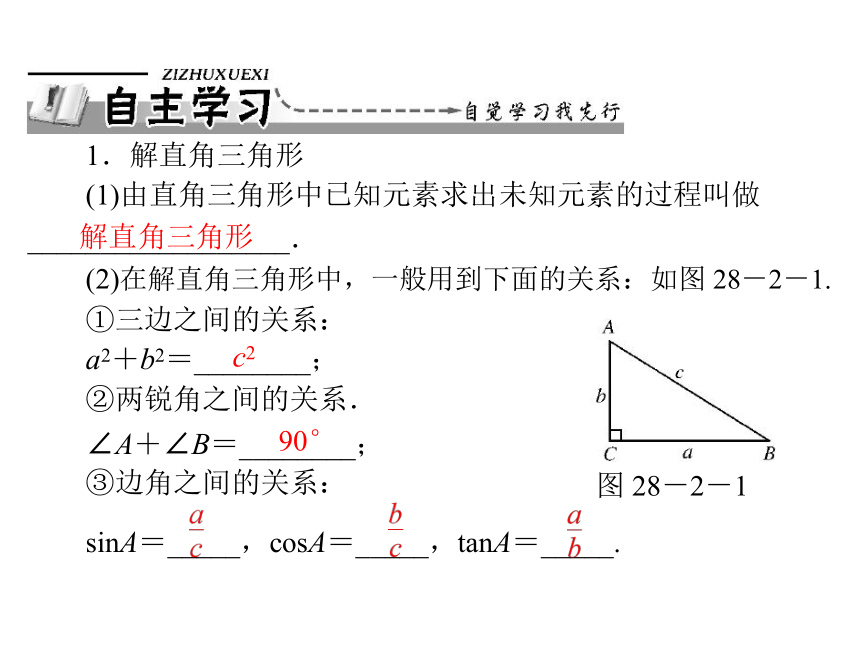
1.解直角三角形
(1)由直角三角形中已知元素求出未知元素的过程叫做
__________________.
解直角三角形
(2)在解直角三角形中,一般用到下面的关系:如图 28-2-1.
90°
①三边之间的关系:
a2+b2=________;
②两锐角之间的关系.
∠A+∠B=________;
③边角之间的关系:
图 28-2-1
sinA=_____,cosA=_____,tanA=_____.
c2
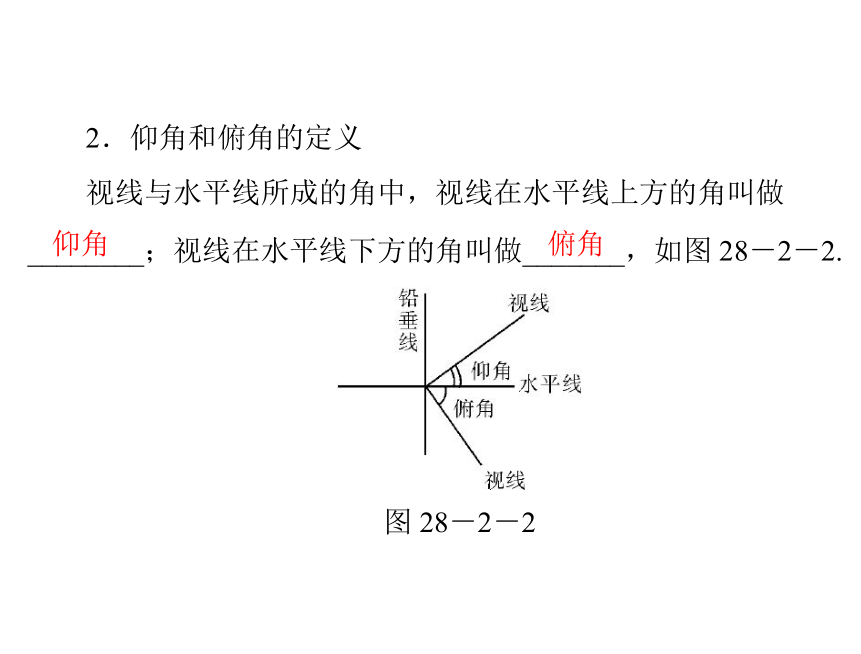
2.仰角和俯角的定义
仰角
俯角
视线与水平线所成的角中,视线在水平线上方的角叫做
________;视线在水平线下方的角叫做_______,如图 28-2-2.
图 28-2-2
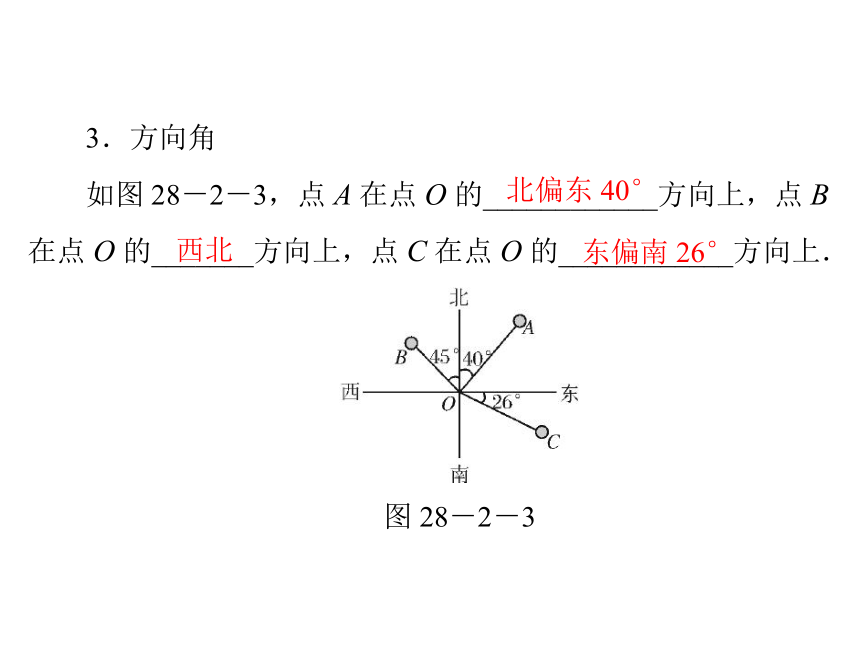
3.方向角
北偏东 40°
西北
东偏南 26°
如图 28-2-3,点 A 在点 O 的____________方向上,点 B
在点 O 的_______方向上,点 C 在点 O 的____________方向上.
图 28-2-3
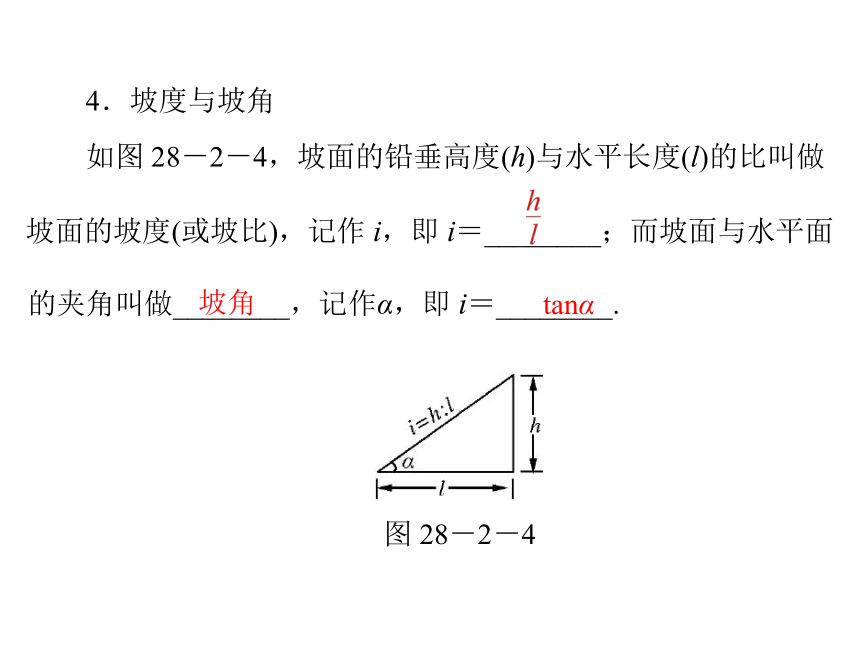
4.坡度与坡角
如图 28-2-4,坡面的铅垂高度(h)与水平长度(l)的比叫做
tanα
的夹角叫做________,记作α,即 i=________.
图 28-2-4
坡面的坡度(或坡比),记作 i,即 i=________;而坡面与水平面
坡角
解直角三角形(重难点)
∴∠B=90°-∠A=30°.
图 D68
图 D69
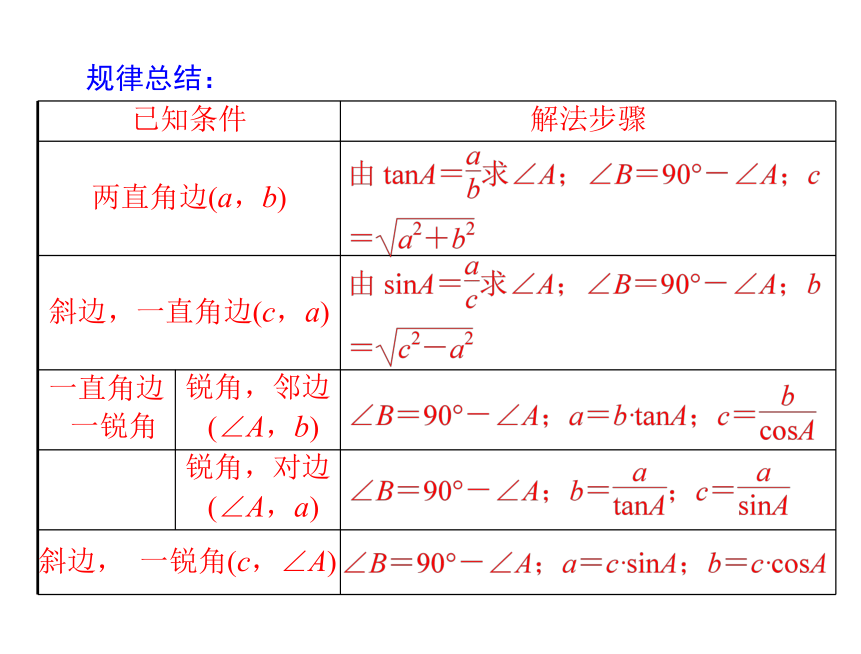
已知条件 解法步骤
两直角边(a,b)
斜边,一直角边(c,a)
一直角边
一锐角 锐角,邻边
(∠A,b)
锐角,对边
(∠A,a)
斜边, 一锐角(c,∠A)
规律总结:
跟踪训练
与方向角有关的计算问题(重点)
例 2:如图 28-2-5,一艘海轮位于灯塔 P 的北偏东65°方
向,距离灯塔 80 海里的 A 处,它沿正南方向航行一段时间后。
到达位于灯塔 P 的南偏东 34°方向上的 B 处.这时,海轮所在的
B 处距离灯塔 P 有多远(精确到 0.01 海里)
图 28-2-5
思路点拨:因为△APB 不是一个直角三角形,所以我们把一
个三角形分解为两个直角三角形△ACP 与△PCB.PC 是东西走向
的一条直线.AB 是南北走向的一条直线,所以 AB 与 PC 是相互
垂直的,即∠ACP与∠BCP均为直角.再通过65°角与∠APC 互
余的关系求∠APC;通过 34°角与∠BPC 互余的关系求∠BPC.
因此,当海轮到达位于灯塔 P 的南偏东 34°方向时,它距离
灯塔 P 大约 130.23 海里.
图 D70
跟踪训练
图 28-2-6
.
∴某市 A 不会受到此次台风的侵袭.
图 D71
解直角三角形的应用(知识综合)
例 3:如图 28-2-7,线段 AB,CD 分别表示甲、乙两建筑
物的高,AB⊥BC,CD⊥BC,从点 A 测得点 D 的俯角α为 30°,
测得 C 点的俯角β为 60°,已知乙建筑物高 CD=40 米,试求甲
建筑物高 AB.
图 28-2-7
∴AB=40+20=60(米).
答:甲建筑物高 AB 为 60 米.
跟踪训练
4.(2010 年广东广州)目前世界上最高的电视塔是广州新电
视塔.如图 28-2-8,新电视塔高 AB 为 610 米,远处有一栋大
楼,某人在楼底 C 处测得塔顶 B 的仰角为 45°,在楼顶 D 处测
得塔顶 B 的仰角为 39°.
(1)求大楼与电视塔之间的距离 AC;
(2)求大楼的高度 CD(精确到 1 米).
图 28-2-8
解:(1)AC=AB=610(米).
(2)DE=AC=610(米),
因为 CD=AE,
所以 CD=AB-DEtan39°=610-610×tan39°≈116(米).
答:(1)大楼与电视塔之间的距离 AC 为 610 米.
(2)大楼的高度 CD 约为 116 米.
28.2
解直角三角形
1.解直角三角形
(1)由直角三角形中已知元素求出未知元素的过程叫做
__________________.
解直角三角形
(2)在解直角三角形中,一般用到下面的关系:如图 28-2-1.
90°
①三边之间的关系:
a2+b2=________;
②两锐角之间的关系.
∠A+∠B=________;
③边角之间的关系:
图 28-2-1
sinA=_____,cosA=_____,tanA=_____.
c2
2.仰角和俯角的定义
仰角
俯角
视线与水平线所成的角中,视线在水平线上方的角叫做
________;视线在水平线下方的角叫做_______,如图 28-2-2.
图 28-2-2
3.方向角
北偏东 40°
西北
东偏南 26°
如图 28-2-3,点 A 在点 O 的____________方向上,点 B
在点 O 的_______方向上,点 C 在点 O 的____________方向上.
图 28-2-3
4.坡度与坡角
如图 28-2-4,坡面的铅垂高度(h)与水平长度(l)的比叫做
tanα
的夹角叫做________,记作α,即 i=________.
图 28-2-4
坡面的坡度(或坡比),记作 i,即 i=________;而坡面与水平面
坡角
解直角三角形(重难点)
∴∠B=90°-∠A=30°.
图 D68
图 D69
已知条件 解法步骤
两直角边(a,b)
斜边,一直角边(c,a)
一直角边
一锐角 锐角,邻边
(∠A,b)
锐角,对边
(∠A,a)
斜边, 一锐角(c,∠A)
规律总结:
跟踪训练
与方向角有关的计算问题(重点)
例 2:如图 28-2-5,一艘海轮位于灯塔 P 的北偏东65°方
向,距离灯塔 80 海里的 A 处,它沿正南方向航行一段时间后。
到达位于灯塔 P 的南偏东 34°方向上的 B 处.这时,海轮所在的
B 处距离灯塔 P 有多远(精确到 0.01 海里)
图 28-2-5
思路点拨:因为△APB 不是一个直角三角形,所以我们把一
个三角形分解为两个直角三角形△ACP 与△PCB.PC 是东西走向
的一条直线.AB 是南北走向的一条直线,所以 AB 与 PC 是相互
垂直的,即∠ACP与∠BCP均为直角.再通过65°角与∠APC 互
余的关系求∠APC;通过 34°角与∠BPC 互余的关系求∠BPC.
因此,当海轮到达位于灯塔 P 的南偏东 34°方向时,它距离
灯塔 P 大约 130.23 海里.
图 D70
跟踪训练
图 28-2-6
.
∴某市 A 不会受到此次台风的侵袭.
图 D71
解直角三角形的应用(知识综合)
例 3:如图 28-2-7,线段 AB,CD 分别表示甲、乙两建筑
物的高,AB⊥BC,CD⊥BC,从点 A 测得点 D 的俯角α为 30°,
测得 C 点的俯角β为 60°,已知乙建筑物高 CD=40 米,试求甲
建筑物高 AB.
图 28-2-7
∴AB=40+20=60(米).
答:甲建筑物高 AB 为 60 米.
跟踪训练
4.(2010 年广东广州)目前世界上最高的电视塔是广州新电
视塔.如图 28-2-8,新电视塔高 AB 为 610 米,远处有一栋大
楼,某人在楼底 C 处测得塔顶 B 的仰角为 45°,在楼顶 D 处测
得塔顶 B 的仰角为 39°.
(1)求大楼与电视塔之间的距离 AC;
(2)求大楼的高度 CD(精确到 1 米).
图 28-2-8
解:(1)AC=AB=610(米).
(2)DE=AC=610(米),
因为 CD=AE,
所以 CD=AB-DEtan39°=610-610×tan39°≈116(米).
答:(1)大楼与电视塔之间的距离 AC 为 610 米.
(2)大楼的高度 CD 约为 116 米.
