[原创]2013年《随堂优化训练》数学第二十七章相似 27.2 相似三角形 第1课时 相似三角形的判定
文档属性
| 名称 | [原创]2013年《随堂优化训练》数学第二十七章相似 27.2 相似三角形 第1课时 相似三角形的判定 |

|
|
| 格式 | zip | ||
| 文件大小 | 271.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-07 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
27.2
第1课时
相似三角形
相似三角形的判定
1.相似三角形
相等
比相等
(1)定义:对应角______,对应边的________的两个三角形
相似.
(3)相似比:相似三角形对应边的______.
∽
比
△ABC∽
△A′B′C′
△ABC相似于△A′B′C′
注意:用“∽”这个符号表示两个图形相似时,应把对应顶
点的字母写在对应的位置上.如图 27-2-1 表示△ABC 与
△DEF 相似,∠A 的对应角是∠D,∠B 的对应角是∠E,∠C 的
对应是∠F,即△ABC∽△DEF,而不能写成△ABC∽△EFD.
图 27-2-1
2.平行线分线段成比例
(1) 定理:三条平行线截两条直线,所得的对应线段的
________.
比相等
比相等
(2)推论:平行于三角形一边的直线截其他两边(或两边的延
长线),所得的对应线段的__________.
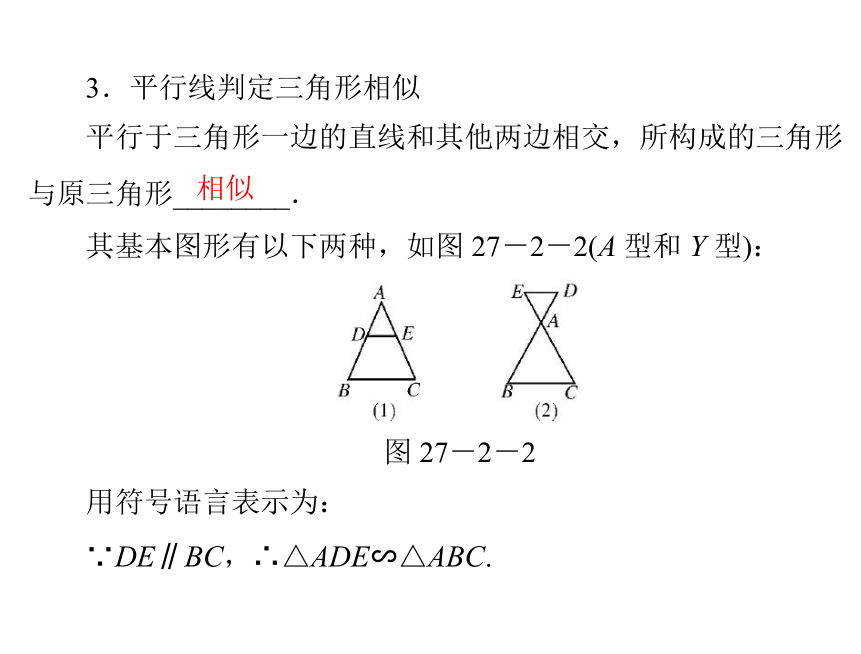
3.平行线判定三角形相似
平行于三角形一边的直线和其他两边相交,所构成的三角形
与原三角形________.
相似
其基本图形有以下两种,如图 27-2-2(A 型和 Y 型):
图 27-2-2
用符号语言表示为:
∵DE∥BC,∴△ADE∽△ABC.
4.判定一般三角形相似的方法
(1)如果两个三角形的____________的比相等,那么这两个
三角形相似.
(2)如果两个三角形的____________的比相等,并且相应的
______相等,那么这两个三角形相似.
(3) 一个三角形的两个 __________ 与另一个三角形的两个
________对应相等,那么这两个三角形相似.
三组对应边
两组对应边
夹角
角
角
5.判定特殊三角形相似的方法
(1)判定直角三角形相似的方法:
①一个锐角对应相等.
②两直角边对应成比例.
③斜边和一组直角边对应成比例.
(2)判定等腰三角形相似的方法:
①顶角相等.
②一对底角相等.
③底和腰对应成比例.
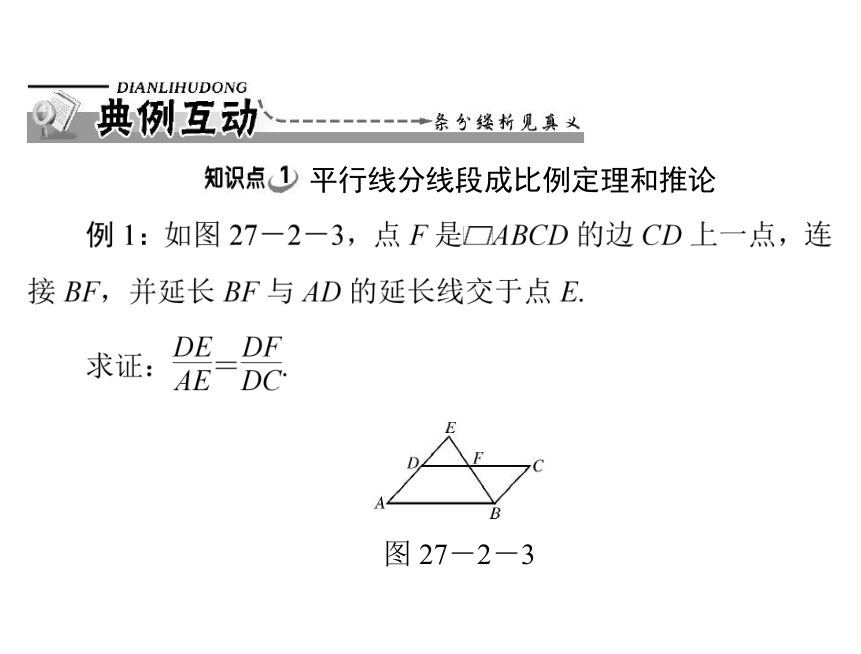
平行线分线段成比例定理和推论
图 27-2-3
思路点拨:结合平行四边形的性质及平行线分线段成比例定
理和推论即可求证.
跟踪训练
图 27-2-4
判定三角形相似的方法
例 2:如图 27-2-5,D,E,F 分别是△ABC 三边的中点,
求证:△ABC∽△EFD.
图 27-2-5
思路点拨:由“三角形的中位线定理”得三边的关系,即可
得证.
例 3:如图 27-2-6 所示,已知∠A=∠D,AD 与 BC 相交
于点 P,AB=8,CD=14,AD=20,求线段 AP 的长.
图 27-2-6
思路点拨:由题意,可证得 AB∥CD,从而△ABP∽△DCP,
由相似三角形对应边成比例及 DP=AD-AP 即可求得 AP 的长.
跟踪训练
2.如图 27-2-7,在△ABC 中,DE∥BC,
AD=EC,DB=1 cm,AE=4 cm,BC=5 cm,
图 27-2-7
求 DE 的长.
3.如图 27-2-8,在正方形 ABCD 中,E 是 AD 的中点,
BM⊥CE,AB=6,求 BM 的长.
图 27-2-8
相似三角形的判定和性质与其他知识的综合运用
例 4:如图 27-2-9,在直角梯形 ABCD 中,AB=7,AD
=2,BC=3,如果边 AB 上的点 P 使得 P,A,D 为顶点的三角
形和以 P,B,C 为顶点的三角形相似,求 AP 的长.
图 27-2-9
规律总结:运用相似三角形对应边成比例建立方程可求线段
的长,求线段长的关键是找准对应顶点,对应边.本题中∠A=
∠B=90°,构成的两直角三角形相似有两种可能,本题的易错点
是:只考虑了这两种情况中的一种对应情况.
跟踪训练
(1)填空:∠APC=________度,∠BPC=________度;
(2)求证:△ACM∽△PMB.
图 27-2-10
解:(1)60
60
(2)由“同弧所对的圆周角相等”,得
∠ABP=∠ACP,∠BPC=∠BAC,
∴△ACM∽△PMB.
27.2
第1课时
相似三角形
相似三角形的判定
1.相似三角形
相等
比相等
(1)定义:对应角______,对应边的________的两个三角形
相似.
(3)相似比:相似三角形对应边的______.
∽
比
△ABC∽
△A′B′C′
△ABC相似于△A′B′C′
注意:用“∽”这个符号表示两个图形相似时,应把对应顶
点的字母写在对应的位置上.如图 27-2-1 表示△ABC 与
△DEF 相似,∠A 的对应角是∠D,∠B 的对应角是∠E,∠C 的
对应是∠F,即△ABC∽△DEF,而不能写成△ABC∽△EFD.
图 27-2-1
2.平行线分线段成比例
(1) 定理:三条平行线截两条直线,所得的对应线段的
________.
比相等
比相等
(2)推论:平行于三角形一边的直线截其他两边(或两边的延
长线),所得的对应线段的__________.
3.平行线判定三角形相似
平行于三角形一边的直线和其他两边相交,所构成的三角形
与原三角形________.
相似
其基本图形有以下两种,如图 27-2-2(A 型和 Y 型):
图 27-2-2
用符号语言表示为:
∵DE∥BC,∴△ADE∽△ABC.
4.判定一般三角形相似的方法
(1)如果两个三角形的____________的比相等,那么这两个
三角形相似.
(2)如果两个三角形的____________的比相等,并且相应的
______相等,那么这两个三角形相似.
(3) 一个三角形的两个 __________ 与另一个三角形的两个
________对应相等,那么这两个三角形相似.
三组对应边
两组对应边
夹角
角
角
5.判定特殊三角形相似的方法
(1)判定直角三角形相似的方法:
①一个锐角对应相等.
②两直角边对应成比例.
③斜边和一组直角边对应成比例.
(2)判定等腰三角形相似的方法:
①顶角相等.
②一对底角相等.
③底和腰对应成比例.
平行线分线段成比例定理和推论
图 27-2-3
思路点拨:结合平行四边形的性质及平行线分线段成比例定
理和推论即可求证.
跟踪训练
图 27-2-4
判定三角形相似的方法
例 2:如图 27-2-5,D,E,F 分别是△ABC 三边的中点,
求证:△ABC∽△EFD.
图 27-2-5
思路点拨:由“三角形的中位线定理”得三边的关系,即可
得证.
例 3:如图 27-2-6 所示,已知∠A=∠D,AD 与 BC 相交
于点 P,AB=8,CD=14,AD=20,求线段 AP 的长.
图 27-2-6
思路点拨:由题意,可证得 AB∥CD,从而△ABP∽△DCP,
由相似三角形对应边成比例及 DP=AD-AP 即可求得 AP 的长.
跟踪训练
2.如图 27-2-7,在△ABC 中,DE∥BC,
AD=EC,DB=1 cm,AE=4 cm,BC=5 cm,
图 27-2-7
求 DE 的长.
3.如图 27-2-8,在正方形 ABCD 中,E 是 AD 的中点,
BM⊥CE,AB=6,求 BM 的长.
图 27-2-8
相似三角形的判定和性质与其他知识的综合运用
例 4:如图 27-2-9,在直角梯形 ABCD 中,AB=7,AD
=2,BC=3,如果边 AB 上的点 P 使得 P,A,D 为顶点的三角
形和以 P,B,C 为顶点的三角形相似,求 AP 的长.
图 27-2-9
规律总结:运用相似三角形对应边成比例建立方程可求线段
的长,求线段长的关键是找准对应顶点,对应边.本题中∠A=
∠B=90°,构成的两直角三角形相似有两种可能,本题的易错点
是:只考虑了这两种情况中的一种对应情况.
跟踪训练
(1)填空:∠APC=________度,∠BPC=________度;
(2)求证:△ACM∽△PMB.
图 27-2-10
解:(1)60
60
(2)由“同弧所对的圆周角相等”,得
∠ABP=∠ACP,∠BPC=∠BAC,
∴△ACM∽△PMB.
