[原创]2013年《随堂优化训练》数学 27.2 相似三角形 第2课时 相似三角形应用举例
文档属性
| 名称 | [原创]2013年《随堂优化训练》数学 27.2 相似三角形 第2课时 相似三角形应用举例 |

|
|
| 格式 | zip | ||
| 文件大小 | 310.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-07 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第 2 课时
相似三角形应用举例
1.相似三角形的实际应用
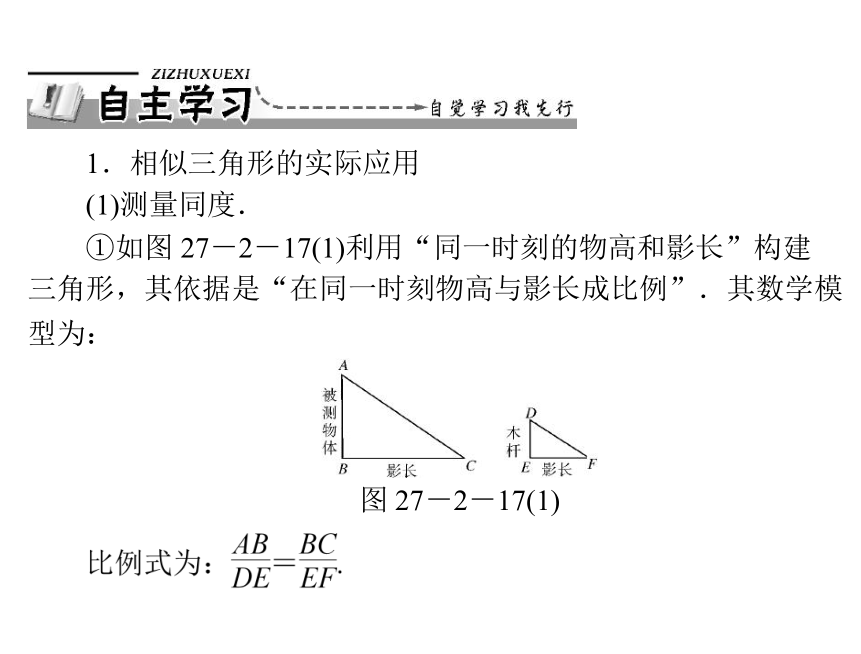
(1)测量同度.
①如图 27-2-17(1)利用“同一时刻的物高和影长”构建
三角形,其依据是“在同一时刻物高与影长成比例”.其数学模
型为:
图 27-2-17(1)
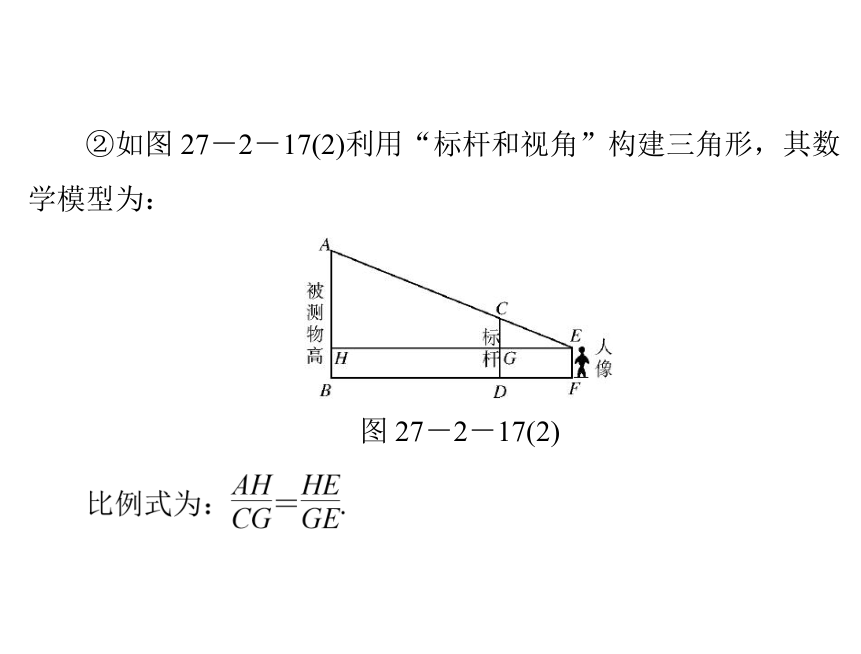
②如图 27-2-17(2)利用“标杆和视角”构建三角形,其数
学模型为:
图 27-2-17(2)
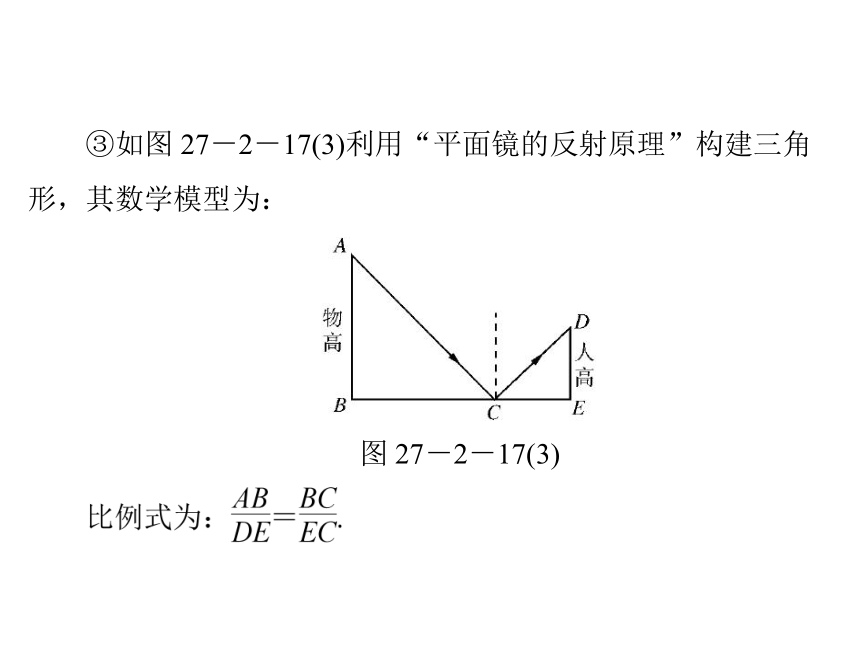
③如图 27-2-17(3)利用“平面镜的反射原理”构建三角
形,其数学模型为:
图 27-2-17(3)
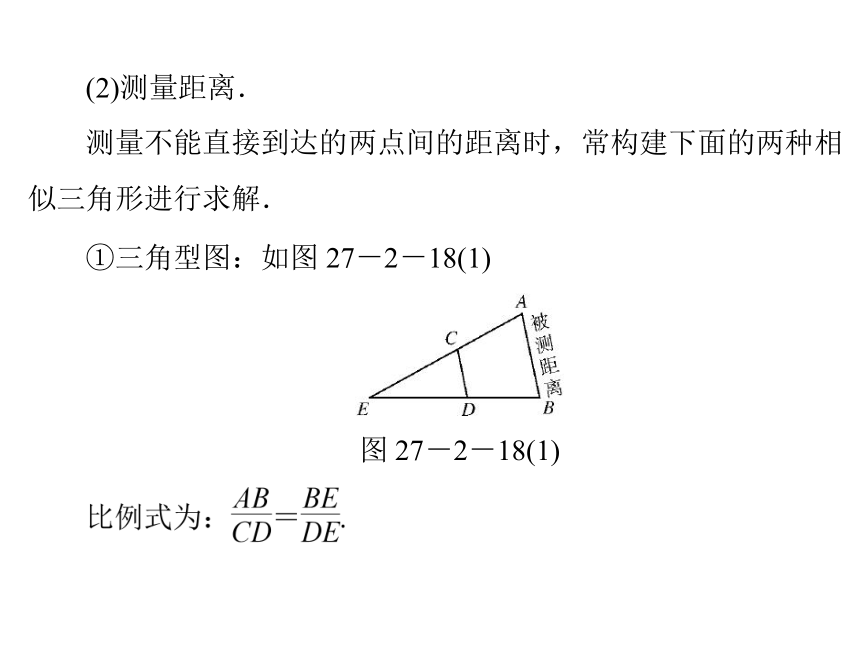
(2)测量距离.
测量不能直接到达的两点间的距离时,常构建下面的两种相
似三角形进行求解.
①三角型图:如图 27-2-18(1)
图 27-2-18(1)
(2)X 型图:如图 27-2-18(2),
图 27-2-18(2)
2.周长与相似比
等于
等于
等于
平方
平方
(1)相似三角形周长的比________相似比.
(2)相似多边形周长的比________相似比.
3.三角形中的“三线”与相似比
相似三角形对应中线的比、对应角平分线的比、对应边上的
高的比都________相似比.
4.面积比与相似比
(1)相似三角形面积的比等于相似比的________.
(2)相似多边形面积的比等于相似比的________.
利用影长测量物体的高度(重点)
例 1:如图 27-2-19,丁轩同学在晚上由路灯 AC 走向路
灯 BD,当他走到点 P 时,发现身后他影子的顶部刚好接触到路
灯 AC 的底部,当他向前再步行 20 m 到达 Q 点时,发现身前他
影子的顶部刚好接触到路灯 BD 的底部,丁轩同学的身高是
1.5 m,两个路灯的高度都是 9 m,则两路灯之间的距离是(
)
A.24 m
C.28 m
B.25 m
D.30 m
图 27-2-19
思路点拨:在同一时刻,物高与影长成比例.
答案:D
跟踪训练
1.如图 27-2-20,在同一时刻,小明测得他的影长为 1
米,距他不远处的一棵槟榔树的影长为 5 米,已知小明的身高为
7.5
1.5 米,则那棵槟榔树的高是______米.
图 27-2-20
相似三角形周长的比
图 27-2-21
思路点拨:先判定这两个三角形相似,再由相似三角形的周
长之比等于相似比,及周长之差,就可求出△ABC 的周长.
跟踪训练
C
相似三角形面积的比(重点)
图 27-2-22
跟踪训练
图 27-2-23
第 2 课时
相似三角形应用举例
1.相似三角形的实际应用
(1)测量同度.
①如图 27-2-17(1)利用“同一时刻的物高和影长”构建
三角形,其依据是“在同一时刻物高与影长成比例”.其数学模
型为:
图 27-2-17(1)
②如图 27-2-17(2)利用“标杆和视角”构建三角形,其数
学模型为:
图 27-2-17(2)
③如图 27-2-17(3)利用“平面镜的反射原理”构建三角
形,其数学模型为:
图 27-2-17(3)
(2)测量距离.
测量不能直接到达的两点间的距离时,常构建下面的两种相
似三角形进行求解.
①三角型图:如图 27-2-18(1)
图 27-2-18(1)
(2)X 型图:如图 27-2-18(2),
图 27-2-18(2)
2.周长与相似比
等于
等于
等于
平方
平方
(1)相似三角形周长的比________相似比.
(2)相似多边形周长的比________相似比.
3.三角形中的“三线”与相似比
相似三角形对应中线的比、对应角平分线的比、对应边上的
高的比都________相似比.
4.面积比与相似比
(1)相似三角形面积的比等于相似比的________.
(2)相似多边形面积的比等于相似比的________.
利用影长测量物体的高度(重点)
例 1:如图 27-2-19,丁轩同学在晚上由路灯 AC 走向路
灯 BD,当他走到点 P 时,发现身后他影子的顶部刚好接触到路
灯 AC 的底部,当他向前再步行 20 m 到达 Q 点时,发现身前他
影子的顶部刚好接触到路灯 BD 的底部,丁轩同学的身高是
1.5 m,两个路灯的高度都是 9 m,则两路灯之间的距离是(
)
A.24 m
C.28 m
B.25 m
D.30 m
图 27-2-19
思路点拨:在同一时刻,物高与影长成比例.
答案:D
跟踪训练
1.如图 27-2-20,在同一时刻,小明测得他的影长为 1
米,距他不远处的一棵槟榔树的影长为 5 米,已知小明的身高为
7.5
1.5 米,则那棵槟榔树的高是______米.
图 27-2-20
相似三角形周长的比
图 27-2-21
思路点拨:先判定这两个三角形相似,再由相似三角形的周
长之比等于相似比,及周长之差,就可求出△ABC 的周长.
跟踪训练
C
相似三角形面积的比(重点)
图 27-2-22
跟踪训练
图 27-2-23
