[原创]2013年《随堂优化训练》数学 27.3 位似[配套课件]
文档属性
| 名称 | [原创]2013年《随堂优化训练》数学 27.3 位似[配套课件] |

|
|
| 格式 | zip | ||
| 文件大小 | 259.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-07 10:21:38 | ||
图片预览





文档简介
(共16张PPT)
27.3
位
似
1.位似图形
一点
平行
位似中心
放大
缩小
(1)定义:如果两个多边形不仅相似,而且对应顶点的连线
相交于______,对应边互相______,像这样的两个图形叫做位似
图形,这个点叫做___________.
(2)作用:可将一个图形________或________.
注意:位似图形上任意一对对应点到位似中心的距离之比等
于位似比.
2.位似图形的画法
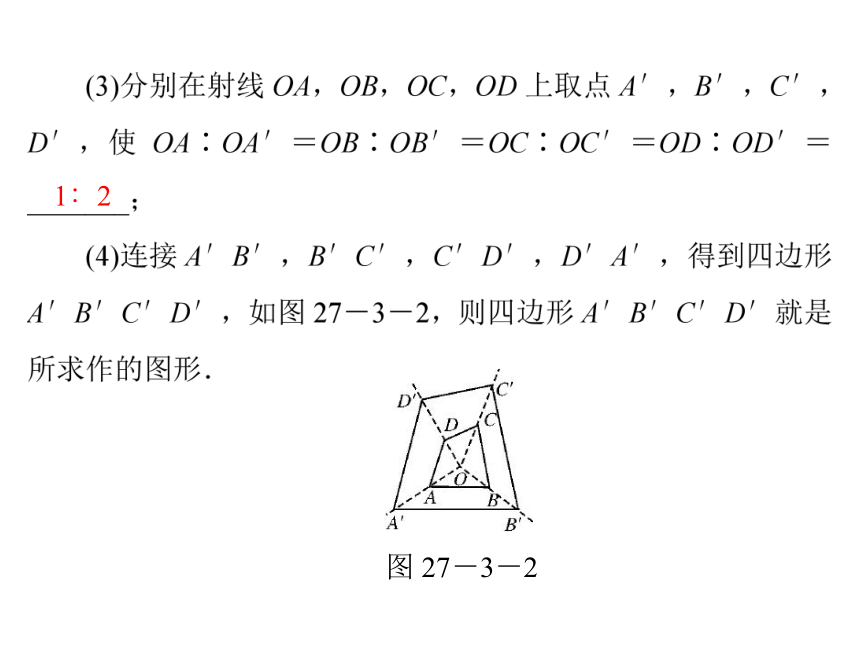
探究:如图 27-3-1,用位似的方法把四边形 ABCD 放大
为原来的 2 倍(要求:位似中心在四边形内).
图 27-3-1
解:(1)在四边形 ABCD 内取一点 O;
(2)以 O 为端点作射线 OA,OB,OC,OD;
1∶2
图 27-3-2
归纳:(1)画位似图形的一般步骤:
①确定__________;
位似中心
外
内
位似中心
②分别连接位似中心和能代表原图的关键点并将其延长;
③根据相似比,确定能代表所作的位似图形的关键点;
④顺次连接上述各点,得到放大或缩小的图形.
(2)位似中心可取在图形的____部、____部、边或顶点上.
(3)位似图形由__________、________两个要素决定.
3.位似变换中对应点坐标变化规律
相似比
k 或-k
在平面直角坐标系中,如果位似是以原点为位似中心,相似
比为 k,那么位似图形对应点的坐标的比等于__________.
位似图形(重点)
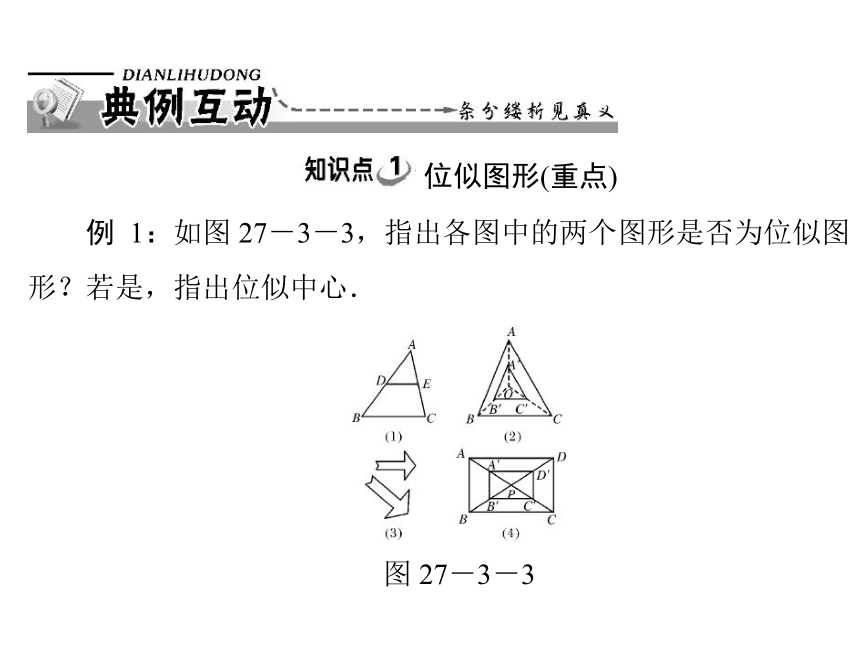
例 1:如图 27-3-3,指出各图中的两个图形是否为位似图
形?若是,指出位似中心.
图 27-3-3
思路点拨:判断标准“①是否相似;②对应点连线是否经过
同一点”.
自主解答:(1),(2),(4)三图中的两个图形都是位似图形,
位似中心分别为点 A,O,P;(3)中的两个图形不是位似图形.
跟踪训练
图 27-3-4
解析:位似中心 O 如图 D59.
图 D59
答案:4
2.在图 27-3-5 中每一组都有两个图形.
图 27-3-5
(1)哪一组中的两个图形是位似图形?
(2)作出位似图形的位似中心.
解:(1)观察得知(4)中的图形不相似,所以它们不是位似图
形;其他五组图均相似,通过画对应点连线得知,只有(1)、(3)
两组是位似图形.
(2)位似中心如图 D60.
图 D60
它们的位似中心分别为点 O,点 P.
位似图形的画法(重难点)
例 2:如图 27-3-6,已知四边形 ABCD 的四个顶点坐标分
别为 A(2,0),B(4,1),C(2,3),D(0,1).作出其以 O 为位似中心,
相似比为 1 的图形,并写出图形的各顶点坐标.
图 27-3-6
自主解答:应用位似中对应点的坐标变化规律,分别取
A′(-2,0),B′(-4,-1),C′(-2,-3),D′(0,-1),顺
次连接 A′,B′,C′,D′,四边形 A′B′C′D′就是要求
的图形,如图 D58.
图 D58
跟踪训练
3.已知:如图 27-3-7 中,点 E(-4,2),F(-1,-1),以
点 O 为位似中心,按比例尺 1∶2,把△EFO 缩小,则点 E 的对
应点 E′的坐标为(
)
图 27-3-7
A.(2,-1)或(-2,1)
C.(2,-1)
B.(8,-4)或(-8,4)
D.(8,-4)
A
图 27-3-8
解:由图 D61 知:A(6,0),B(6,4),C(0,4),利用位似图形对
应点的坐标的变化规律,分别取点 A′(3,0),B′(3,2),C′(0,2),
依次连接点 O,A′,B′,C′,则四边形 OA′B′C′就是所
求作的四边形,如图 15.
图 D61
27.3
位
似
1.位似图形
一点
平行
位似中心
放大
缩小
(1)定义:如果两个多边形不仅相似,而且对应顶点的连线
相交于______,对应边互相______,像这样的两个图形叫做位似
图形,这个点叫做___________.
(2)作用:可将一个图形________或________.
注意:位似图形上任意一对对应点到位似中心的距离之比等
于位似比.
2.位似图形的画法
探究:如图 27-3-1,用位似的方法把四边形 ABCD 放大
为原来的 2 倍(要求:位似中心在四边形内).
图 27-3-1
解:(1)在四边形 ABCD 内取一点 O;
(2)以 O 为端点作射线 OA,OB,OC,OD;
1∶2
图 27-3-2
归纳:(1)画位似图形的一般步骤:
①确定__________;
位似中心
外
内
位似中心
②分别连接位似中心和能代表原图的关键点并将其延长;
③根据相似比,确定能代表所作的位似图形的关键点;
④顺次连接上述各点,得到放大或缩小的图形.
(2)位似中心可取在图形的____部、____部、边或顶点上.
(3)位似图形由__________、________两个要素决定.
3.位似变换中对应点坐标变化规律
相似比
k 或-k
在平面直角坐标系中,如果位似是以原点为位似中心,相似
比为 k,那么位似图形对应点的坐标的比等于__________.
位似图形(重点)
例 1:如图 27-3-3,指出各图中的两个图形是否为位似图
形?若是,指出位似中心.
图 27-3-3
思路点拨:判断标准“①是否相似;②对应点连线是否经过
同一点”.
自主解答:(1),(2),(4)三图中的两个图形都是位似图形,
位似中心分别为点 A,O,P;(3)中的两个图形不是位似图形.
跟踪训练
图 27-3-4
解析:位似中心 O 如图 D59.
图 D59
答案:4
2.在图 27-3-5 中每一组都有两个图形.
图 27-3-5
(1)哪一组中的两个图形是位似图形?
(2)作出位似图形的位似中心.
解:(1)观察得知(4)中的图形不相似,所以它们不是位似图
形;其他五组图均相似,通过画对应点连线得知,只有(1)、(3)
两组是位似图形.
(2)位似中心如图 D60.
图 D60
它们的位似中心分别为点 O,点 P.
位似图形的画法(重难点)
例 2:如图 27-3-6,已知四边形 ABCD 的四个顶点坐标分
别为 A(2,0),B(4,1),C(2,3),D(0,1).作出其以 O 为位似中心,
相似比为 1 的图形,并写出图形的各顶点坐标.
图 27-3-6
自主解答:应用位似中对应点的坐标变化规律,分别取
A′(-2,0),B′(-4,-1),C′(-2,-3),D′(0,-1),顺
次连接 A′,B′,C′,D′,四边形 A′B′C′D′就是要求
的图形,如图 D58.
图 D58
跟踪训练
3.已知:如图 27-3-7 中,点 E(-4,2),F(-1,-1),以
点 O 为位似中心,按比例尺 1∶2,把△EFO 缩小,则点 E 的对
应点 E′的坐标为(
)
图 27-3-7
A.(2,-1)或(-2,1)
C.(2,-1)
B.(8,-4)或(-8,4)
D.(8,-4)
A
图 27-3-8
解:由图 D61 知:A(6,0),B(6,4),C(0,4),利用位似图形对
应点的坐标的变化规律,分别取点 A′(3,0),B′(3,2),C′(0,2),
依次连接点 O,A′,B′,C′,则四边形 OA′B′C′就是所
求作的四边形,如图 15.
图 D61
