[原创]2013年《随堂优化训练》数学 人教版 九年级 上册 第二十四章 圆 24.2 点、直线、圆和圆的位置关系 第1课时 点和圆的位置关系
文档属性
| 名称 | [原创]2013年《随堂优化训练》数学 人教版 九年级 上册 第二十四章 圆 24.2 点、直线、圆和圆的位置关系 第1课时 点和圆的位置关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 93.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-07 00:00:00 | ||
图片预览




文档简介
(共10张PPT)
24.2
点、直线、圆和圆的位置关系
第 1 课时
点和圆的位置关系
1.点与圆的位置关系
>
=
<
三
设⊙O 的半径为 r,点 P 到圆的距离为 d,则有:
点 P 在圆外 d______r;
点 P 在圆上 d______r;
点 P 在圆内 d______r.
2.定理
不在同一直线上的______个点确定一个圆.
3.三角形的外接圆
(1) 经过三角形的三个顶点可以作______个圆,并且只能画
一个圆,这个圆叫做三角形的外接圆.
(2)外接圆的圆心是三角形_____________________的交点,
叫做这个三角形的外心.它到三角形三个顶点的距离相等.
(3)锐角三角形外心在三角形内部;直角三角形外心在
_________________;钝角三角形外心在三角形外部.
一
三条边的垂直平分线
斜边中点
假设命题的结论不成立
4.用反证法证明命题的一般步骤
(1)_______________________;
(2)从假设出发,经过推理论证,得出矛盾;
(3)由矛盾断定所作假设不正确,从而得到命题成立.
点和圆的位置关系
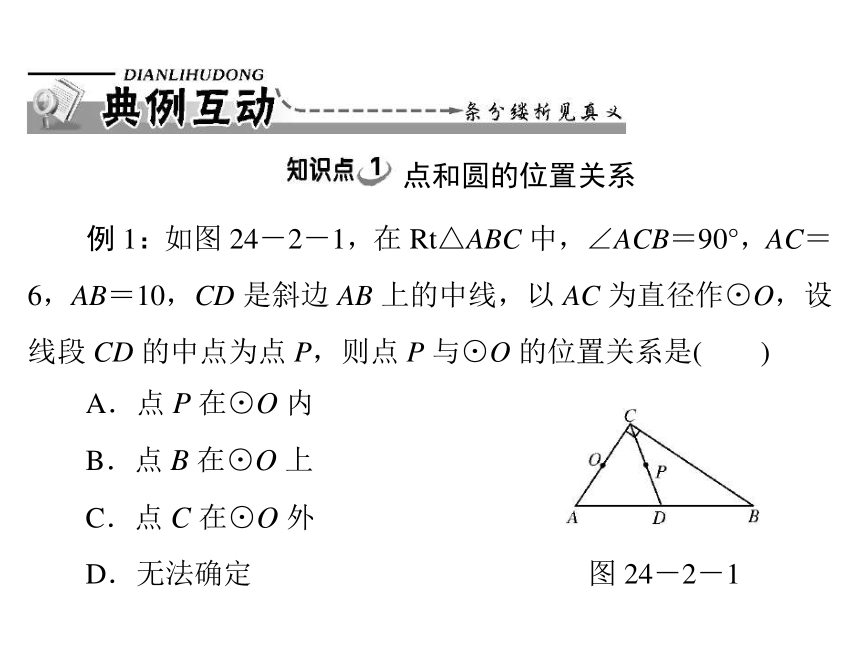
A.点 P 在⊙O 内
B.点 B 在⊙O 上
C.点 C 在⊙O 外
D.无法确定
图 24-2-1
思路点拨:先由勾股定理等性质算出点与圆心的距离 d,再
根据点到圆心的距离与半径的大小关系作出判断.
答案:A
跟踪训练
B
A
M,C
C
A.a=15,b=12,c=1
C.a=5,b=12,c=13
B.a=5,b=12,c=12
D.a=5,b=12,c=14
反证法的应用
例 2:用反证法证明:等腰三角形的底角都是锐角.
思路点拨:写出“已知、求证”后,再根据反证法证明命题
的一般步骤进行证明.
解:已知:在△ABC 中,AB=AC.求证:∠B,∠C 都是
锐角.
证明:假设∠B,∠C 不都是锐角.
∵AB=AC,∴∠B=∠C.
而∠B 和∠C 都是直角或钝角,
∴∠B+∠C≥90°+90°=180°.
∴∠A+∠B+∠C >180°.
这与三角形内角和定理矛盾.
∴等腰三角形的底角都是锐角.
跟踪训练
3.用反证法证明命题“三角形中必须有一个内角小于或等
)
D
于 60°”时,首先应假设这个三角形中(
A.有一个内角小于 60°
B.每一个内角都小于 60°
C.有一个内角大于 60°
D.每一个内角都大于 60°
24.2
点、直线、圆和圆的位置关系
第 1 课时
点和圆的位置关系
1.点与圆的位置关系
>
=
<
三
设⊙O 的半径为 r,点 P 到圆的距离为 d,则有:
点 P 在圆外 d______r;
点 P 在圆上 d______r;
点 P 在圆内 d______r.
2.定理
不在同一直线上的______个点确定一个圆.
3.三角形的外接圆
(1) 经过三角形的三个顶点可以作______个圆,并且只能画
一个圆,这个圆叫做三角形的外接圆.
(2)外接圆的圆心是三角形_____________________的交点,
叫做这个三角形的外心.它到三角形三个顶点的距离相等.
(3)锐角三角形外心在三角形内部;直角三角形外心在
_________________;钝角三角形外心在三角形外部.
一
三条边的垂直平分线
斜边中点
假设命题的结论不成立
4.用反证法证明命题的一般步骤
(1)_______________________;
(2)从假设出发,经过推理论证,得出矛盾;
(3)由矛盾断定所作假设不正确,从而得到命题成立.
点和圆的位置关系
A.点 P 在⊙O 内
B.点 B 在⊙O 上
C.点 C 在⊙O 外
D.无法确定
图 24-2-1
思路点拨:先由勾股定理等性质算出点与圆心的距离 d,再
根据点到圆心的距离与半径的大小关系作出判断.
答案:A
跟踪训练
B
A
M,C
C
A.a=15,b=12,c=1
C.a=5,b=12,c=13
B.a=5,b=12,c=12
D.a=5,b=12,c=14
反证法的应用
例 2:用反证法证明:等腰三角形的底角都是锐角.
思路点拨:写出“已知、求证”后,再根据反证法证明命题
的一般步骤进行证明.
解:已知:在△ABC 中,AB=AC.求证:∠B,∠C 都是
锐角.
证明:假设∠B,∠C 不都是锐角.
∵AB=AC,∴∠B=∠C.
而∠B 和∠C 都是直角或钝角,
∴∠B+∠C≥90°+90°=180°.
∴∠A+∠B+∠C >180°.
这与三角形内角和定理矛盾.
∴等腰三角形的底角都是锐角.
跟踪训练
3.用反证法证明命题“三角形中必须有一个内角小于或等
)
D
于 60°”时,首先应假设这个三角形中(
A.有一个内角小于 60°
B.每一个内角都小于 60°
C.有一个内角大于 60°
D.每一个内角都大于 60°
同课章节目录
