[原创]2013年《随堂优化训练》数学 24.2 点、直线、圆和圆的位置关系 第2课时 直线和圆的位置关系
文档属性
| 名称 | [原创]2013年《随堂优化训练》数学 24.2 点、直线、圆和圆的位置关系 第2课时 直线和圆的位置关系 |  | |
| 格式 | zip | ||
| 文件大小 | 235.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-07 10:30:14 | ||
图片预览





文档简介
(共16张PPT)
第 2 课时
直线和圆的位置关系
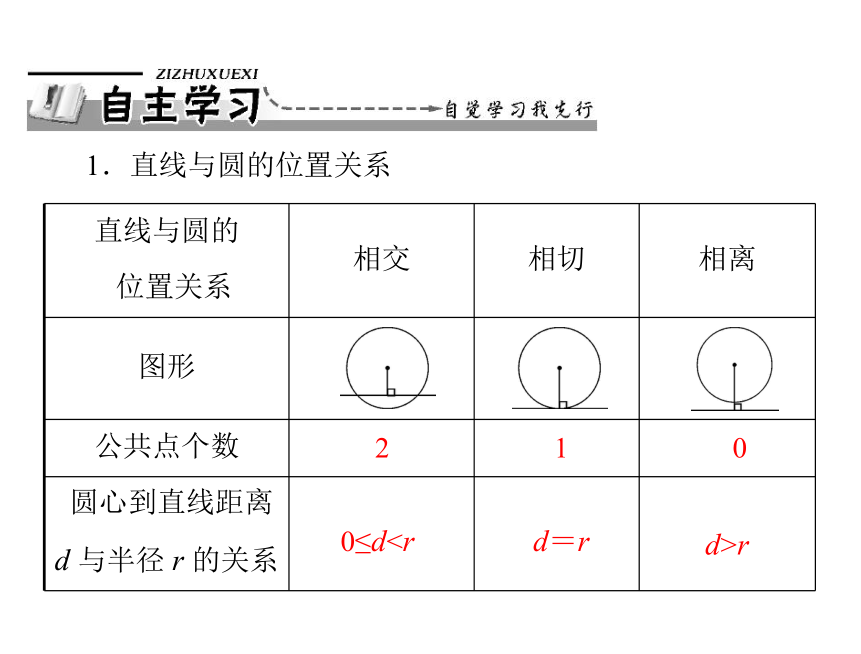
直线与圆的
位置关系 相交 相切 相离
图形
公共点个数
圆心到直线距离
d 与半径 r 的关系
1.直线与圆的位置关系
2
1
0
0≤dd=r
d>r
2.切线的判定定理及性质定理
(1)判定定理:经过半径的外端并且垂直于这条半径的直线
是圆的__________.
切线
垂直
线段
(2)性质定理:圆的切线________于过切点的半径.
3.切线长的概念
相等
圆心
经过圆外一点作圆的切线,这点和切点之间的________的
长,叫做这点到圆的切线长.
4.切线长定理
从圆外一点可以引圆的两条切线,它们的切线长________,
这一点和________的连线平分两条切线的夹角.
5.三角形的内切圆
相切
角平分线
内切圆
相等
与三角形各边都________的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条__________的交点.
6.三角形的内心
(1)三角形的________的圆心叫做三角形的内心.
(2)三角形内心的性质:三角形的内心到三角形三边的距离
________.
切线的判定定理及性质定理
例 1:如图 24-2-9 所示,点 A 是⊙O 外一点,OA 交⊙O
于点 B,AC 是⊙O 的切线,切点是 C,且∠A=30°,BC=1.求
⊙O 的半径.
图 24-2-9
规律总结:有切线时连接圆心和切点,得半径垂直切线.
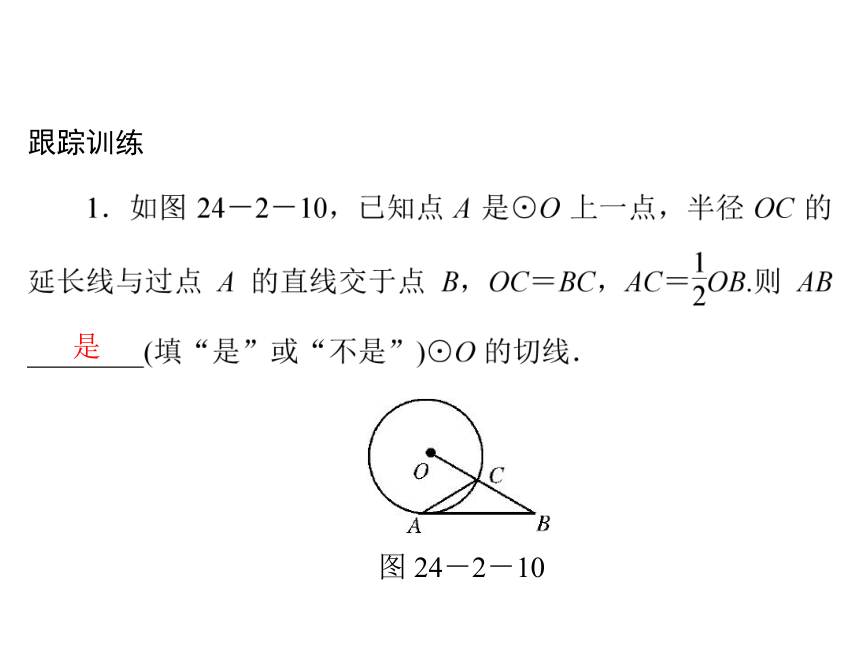
跟踪训练
是
图 24-2-10
2.如图 24-2-11,线段 AB 经过圆心 O,交⊙O 于点 A,
C,∠BAD=∠B=30°,边 BD 交圆于点 D.BD 是⊙O 的切线吗?
为什么?
图 24-2-11
解:BD 是⊙O 的切线.
连接 OD, ∵OD=OA,∠A=30°,
∴∠DOB=60°.
∵∠B=30°,∴∠ODB=90°.
∴BD 是⊙O 的切线.
切线长定理
例 2:如图 24-2-12,在 Rt△ABC 中,∠C=90°,点 O
在 BC 上,以点 O 为圆心,OC 为半径的⊙O 切 AB 于点 D,交
BC 于点 E.若 AC=5,BC=12,求 BE 的长.
图 24-2-12
思路点拨:连接 OD,利用切线长定理与勾股定理求圆的半径.
跟踪训练
3.一个钢管放在 V 形架内,图 24-2-13 是其截面图,O
为钢管的圆心.如果钢管的半径为25 cm,∠MPN=60°,则OP
=(
)
A
图 24-2-13
4.如图 24-2-14,PA ,PB 分别切⊙O 于点 A,B,点 E
60°
是⊙O 上一点,且∠AEB=60°,则∠P=________.
图 24-2-14
三角形的内心
例 3:如图 24-2-15,已知点 E 是△ABC 的内心,∠A 的
平分线交 BC 于点 F,且与△ABC 的外接圆相交于点 D.求证:
∠ DBE=∠DEB.
图 24-2-15
思路点拨:点 E 是△ABC 的内心,AD,BE 分别是∠BAC
和∠ABC 的角平分线,又同弦所对的圆周角相等,易证明∠DBE
=∠DEB.
证明:∵点 E 是△ABC 的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
∵∠CBD=∠CAD,∠DEB=∠BAD+∠ABE,∠DBE=
∠CBD+∠EBC,
∴∠DBE=∠DEB.
跟踪训练
5.如图 24-2-16,⊙O 为△ABC 的内切圆,D,E,F 为
切点,∠DOB=73°,∠DOE=120°, 则∠DOF=____,∠C
=______,∠A=______.
146°
60°
86°
图 24-2-16
2
图 24-2-17
第 2 课时
直线和圆的位置关系
直线与圆的
位置关系 相交 相切 相离
图形
公共点个数
圆心到直线距离
d 与半径 r 的关系
1.直线与圆的位置关系
2
1
0
0≤d
d>r
2.切线的判定定理及性质定理
(1)判定定理:经过半径的外端并且垂直于这条半径的直线
是圆的__________.
切线
垂直
线段
(2)性质定理:圆的切线________于过切点的半径.
3.切线长的概念
相等
圆心
经过圆外一点作圆的切线,这点和切点之间的________的
长,叫做这点到圆的切线长.
4.切线长定理
从圆外一点可以引圆的两条切线,它们的切线长________,
这一点和________的连线平分两条切线的夹角.
5.三角形的内切圆
相切
角平分线
内切圆
相等
与三角形各边都________的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条__________的交点.
6.三角形的内心
(1)三角形的________的圆心叫做三角形的内心.
(2)三角形内心的性质:三角形的内心到三角形三边的距离
________.
切线的判定定理及性质定理
例 1:如图 24-2-9 所示,点 A 是⊙O 外一点,OA 交⊙O
于点 B,AC 是⊙O 的切线,切点是 C,且∠A=30°,BC=1.求
⊙O 的半径.
图 24-2-9
规律总结:有切线时连接圆心和切点,得半径垂直切线.
跟踪训练
是
图 24-2-10
2.如图 24-2-11,线段 AB 经过圆心 O,交⊙O 于点 A,
C,∠BAD=∠B=30°,边 BD 交圆于点 D.BD 是⊙O 的切线吗?
为什么?
图 24-2-11
解:BD 是⊙O 的切线.
连接 OD, ∵OD=OA,∠A=30°,
∴∠DOB=60°.
∵∠B=30°,∴∠ODB=90°.
∴BD 是⊙O 的切线.
切线长定理
例 2:如图 24-2-12,在 Rt△ABC 中,∠C=90°,点 O
在 BC 上,以点 O 为圆心,OC 为半径的⊙O 切 AB 于点 D,交
BC 于点 E.若 AC=5,BC=12,求 BE 的长.
图 24-2-12
思路点拨:连接 OD,利用切线长定理与勾股定理求圆的半径.
跟踪训练
3.一个钢管放在 V 形架内,图 24-2-13 是其截面图,O
为钢管的圆心.如果钢管的半径为25 cm,∠MPN=60°,则OP
=(
)
A
图 24-2-13
4.如图 24-2-14,PA ,PB 分别切⊙O 于点 A,B,点 E
60°
是⊙O 上一点,且∠AEB=60°,则∠P=________.
图 24-2-14
三角形的内心
例 3:如图 24-2-15,已知点 E 是△ABC 的内心,∠A 的
平分线交 BC 于点 F,且与△ABC 的外接圆相交于点 D.求证:
∠ DBE=∠DEB.
图 24-2-15
思路点拨:点 E 是△ABC 的内心,AD,BE 分别是∠BAC
和∠ABC 的角平分线,又同弦所对的圆周角相等,易证明∠DBE
=∠DEB.
证明:∵点 E 是△ABC 的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
∵∠CBD=∠CAD,∠DEB=∠BAD+∠ABE,∠DBE=
∠CBD+∠EBC,
∴∠DBE=∠DEB.
跟踪训练
5.如图 24-2-16,⊙O 为△ABC 的内切圆,D,E,F 为
切点,∠DOB=73°,∠DOE=120°, 则∠DOF=____,∠C
=______,∠A=______.
146°
60°
86°
图 24-2-16
2
图 24-2-17
同课章节目录
