2021-2022学年人教版九年级数学下册27.1图形的相似优生辅导测评(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.1图形的相似优生辅导测评(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 255.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 11:50:43 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学下册《27.1图形的相似》优生辅导测评(附答案)
一.选择题(共11小题,满分44分)
1.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是( )
A. B. C. D.
2.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,若AB=2,BC=4,DF=9,则EF的长是( )
A.3 B.6 C.7 D.8
3.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A. B. C.6 D.10
4.如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
A. B. C. D.
5.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则=( )
A. B.2 C. D.
6.如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果=,那么等于( )
A. B. C. D.
7.如图,三角形ABC中,D、E、F分别是AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=1:2,BC=30cm,则FC的长为( )
A.10cm B.20cm C.5cm D.6cm
8.若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )
A.增加了10% B.减少了10%
C.增加了(1+10%) D.没有改变
9.若==,且3a﹣2b+c=3,则2a+4b﹣3c的值是( )
A.14 B.42 C.7 D.
10.如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )
A. B. C. D.
二.填空题(共9小题,满分36分)
11.若,则= .
12.P为线段AB=8cm的黄金分割点,则AP= cm.
13.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AE:EC=2:3,DE:BC= .
14.已知,则k的值为 .
15.在1:500000的地图上,A、B两地的距离是64 cm,则这两地间的实际距离是 km.
16.如图,AD是△ABC的中线,E是AC上的一点,且AE:EC=1:3,设BE与AD交于G,则AG:GD= .
17.若线段a,b,c满足关系=,=,则a:b:c= .
18.如图,梯形ABCD中,,则= .
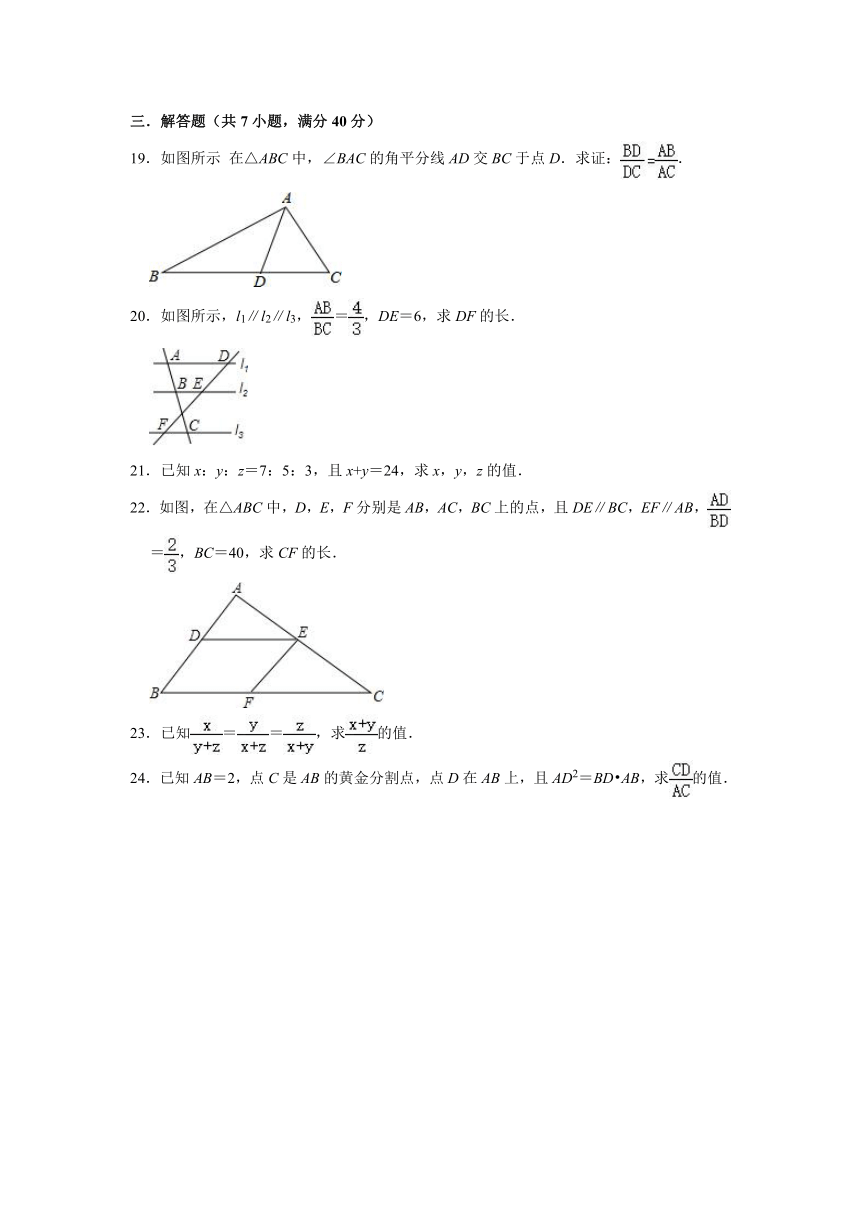
三.解答题(共7小题,满分40分)
19.如图所示 在△ABC中,∠BAC的角平分线AD交BC于点D.求证:.
20.如图所示,l1∥l2∥l3,=,DE=6,求DF的长.
21.已知x:y:z=7:5:3,且x+y=24,求x,y,z的值.
22.如图,在△ABC中,D,E,F分别是AB,AC,BC上的点,且DE∥BC,EF∥AB,=,BC=40,求CF的长.
23.已知==,求的值.
24.已知AB=2,点C是AB的黄金分割点,点D在AB上,且AD2=BD AB,求的值.
参考答案
一.选择题(共11小题,满分44分)
1.解:∵DE∥BC,
∴,
∴当时,,
∴EF∥CD,故C选项符合题意;
而A,B,D选项不能得出EF∥CD,
故选:C.
2.解:∵AD∥BE∥CF,
∴=,
∵AB=2,BC=4,DF=9,
∴=,
解得EF=6.
故选:B.
3.解:∵l1∥l2∥l3,
∴,
即,
解得:EF=6.
故选:C.
4.解:∵BG∥DF,∴=,A正确,C错误;
∴=,B 正确;
∵AD∥BC,∴∠A=∠C,
∵BG∥DF,∴∠BEC=∠DFA,
∴△BEC∽△DFA,
∴=,D正确,
故选:C.
5.解:∵AH=2,HB=1,
∴AB=AH+BH=3,
∵l1∥l2∥l3,
∴==.故选:A.
6.解:∵DE∥AB,
∴=,
∵AD为△ABC的角平分线,
∴=;故选:B.
7.解:∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形,
∴BF=DE.
∵AD:DB=1:2,
∴AD:AB=1:3.
∵DE∥BC,
∴DE:BC=AD:AB=1:3,即DE:30=1:3,
∴DE=10,
∴BF=10.
故FC的长为20cm.故选:B.
8.解:∵△ABC的每条边长增加各自的10%得△A′B′C′,
∴△ABC与△A′B′C′的三边对应成比例,
∴△ABC∽△A′B′C′,
∴∠B′=∠B.
故选:D.
9.解:设a=5k,则b=7k,c=8k,
又3a﹣2b+c=3,则15k﹣14k+8k=3,
得k=,
即a=,b=,c=,
所以2a+4b﹣3c=.故选D.
10.A.∵EF∥AB,∴=,故本选项正确,
B.∵DE∥BC,
∴=,
∵EF∥AB,
∴DE=BF,
∴=,
∴=,
故本选项正确,
C.∵EF∥AB,
∴=,
∵CF≠DE,
∴≠,
故本选项错误,
D.∵EF∥AB,
∴=,
∴=,
故本选项正确,
故选:C.
二.填空题(共9小题,满分36分)
11.解:两边都减2,得
==,
故答案为:.
12.解:由于P为线段AB=8cm的黄金分割点,
则AP=8×=4﹣4,
或AP=8﹣(4﹣4)=12﹣4.
故本题答案为:4﹣4或12﹣4.
13.解:∵DE∥BC,
∴=,
又AE:EC=2:3,即AE:AC=2:5,
∴DE:BC=2:5.
故答案为:2:5.
14.解:分两种情况:
①当a+b+c=0时,则有a+b=﹣c,
所以k===﹣2;
②当a+b+c≠0时,
∵,
∴k==1.
故答案为﹣2或1.
15.解:设A,B两地的实际距离为xkm,则:
=,解得x=32000000cm=320km,
∴两地间的实际距离是320km.
16.解:作DF∥BE交AC于F,
∵AD是△ABC的中线,
∴EF=FC=EC,
∵AE:EC=1:3,设AE=x,EC=3x,
∴EF=1.5x.
∵DF∥BE,
∴△AGE∽△ADF,
∴,
∴,
∴.
故答案为:2:3.
17.解:∵=,=,
∴=,
∴a:b:c=9:12:20.
故填9:12:20.
18.解:∵四边形ABCD是梯形,
∴AD∥BC;
又EF∥BC,
∴AD∥EF∥BC,
∴=(平行线分线段成比例);
∵,
∴=,
∴=(等量代换).
故答案是:.
三.解答题(共7小题,满分40分)
19.证明:如图,
过B作BE∥AC,交AD的延长线交于E.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵BE∥AC,
∴∠CAD=∠E.
∴∠BAD=∠E,
∴AB=BE.
又∵BE∥AC,
∴△BDE∽△CDA,
∴BE:AC=BD:DC,
∴.
20.解:∵l1∥l2∥l3,
∴==,
即,
解得:EF=4.5,
∴DF=DE+EF=6+4.5=10.5.
21.解:由x:y:z=7:5:3,得
x=7a,y=5a,z=3a.
由x+y=24得
7a+5a=24.
解得a=2,
x=7a=14,y=5a=10,z=3a=6.
22.解:∵DE∥BC,
∴==,又BC=40,
∴DE=16,
∵DE∥BC,EF∥AB,
∴四边形DBFE是平行四边形,
∴BF=DE=16,
∴CF=BC﹣BF=24.
23.解:①当x+y+z≠0时,由等比性质,得
==.
由反比性质,得
∴==2.
②当x+y+z=0时,=﹣1.
24.解:∵D在AB上,且AD2=BD AB,
∴点D是AB的黄金分割点,且AD=AB=﹣1,
而点C是AB的黄金分割点,
当C、D重合时,=0,
当C、D不重合时,AC=3﹣,
∴CD=﹣1﹣(3﹣)=2﹣4,
∴==.
一.选择题(共11小题,满分44分)
1.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是( )
A. B. C. D.
2.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,若AB=2,BC=4,DF=9,则EF的长是( )
A.3 B.6 C.7 D.8
3.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A. B. C.6 D.10
4.如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
A. B. C. D.
5.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则=( )
A. B.2 C. D.
6.如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果=,那么等于( )
A. B. C. D.
7.如图,三角形ABC中,D、E、F分别是AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=1:2,BC=30cm,则FC的长为( )
A.10cm B.20cm C.5cm D.6cm
8.若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )
A.增加了10% B.减少了10%
C.增加了(1+10%) D.没有改变
9.若==,且3a﹣2b+c=3,则2a+4b﹣3c的值是( )
A.14 B.42 C.7 D.
10.如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )
A. B. C. D.
二.填空题(共9小题,满分36分)
11.若,则= .
12.P为线段AB=8cm的黄金分割点,则AP= cm.
13.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AE:EC=2:3,DE:BC= .
14.已知,则k的值为 .
15.在1:500000的地图上,A、B两地的距离是64 cm,则这两地间的实际距离是 km.
16.如图,AD是△ABC的中线,E是AC上的一点,且AE:EC=1:3,设BE与AD交于G,则AG:GD= .
17.若线段a,b,c满足关系=,=,则a:b:c= .
18.如图,梯形ABCD中,,则= .
三.解答题(共7小题,满分40分)
19.如图所示 在△ABC中,∠BAC的角平分线AD交BC于点D.求证:.
20.如图所示,l1∥l2∥l3,=,DE=6,求DF的长.
21.已知x:y:z=7:5:3,且x+y=24,求x,y,z的值.
22.如图,在△ABC中,D,E,F分别是AB,AC,BC上的点,且DE∥BC,EF∥AB,=,BC=40,求CF的长.
23.已知==,求的值.
24.已知AB=2,点C是AB的黄金分割点,点D在AB上,且AD2=BD AB,求的值.
参考答案
一.选择题(共11小题,满分44分)
1.解:∵DE∥BC,
∴,
∴当时,,
∴EF∥CD,故C选项符合题意;
而A,B,D选项不能得出EF∥CD,
故选:C.
2.解:∵AD∥BE∥CF,
∴=,
∵AB=2,BC=4,DF=9,
∴=,
解得EF=6.
故选:B.
3.解:∵l1∥l2∥l3,
∴,
即,
解得:EF=6.
故选:C.
4.解:∵BG∥DF,∴=,A正确,C错误;
∴=,B 正确;
∵AD∥BC,∴∠A=∠C,
∵BG∥DF,∴∠BEC=∠DFA,
∴△BEC∽△DFA,
∴=,D正确,
故选:C.
5.解:∵AH=2,HB=1,
∴AB=AH+BH=3,
∵l1∥l2∥l3,
∴==.故选:A.
6.解:∵DE∥AB,
∴=,
∵AD为△ABC的角平分线,
∴=;故选:B.
7.解:∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形,
∴BF=DE.
∵AD:DB=1:2,
∴AD:AB=1:3.
∵DE∥BC,
∴DE:BC=AD:AB=1:3,即DE:30=1:3,
∴DE=10,
∴BF=10.
故FC的长为20cm.故选:B.
8.解:∵△ABC的每条边长增加各自的10%得△A′B′C′,
∴△ABC与△A′B′C′的三边对应成比例,
∴△ABC∽△A′B′C′,
∴∠B′=∠B.
故选:D.
9.解:设a=5k,则b=7k,c=8k,
又3a﹣2b+c=3,则15k﹣14k+8k=3,
得k=,
即a=,b=,c=,
所以2a+4b﹣3c=.故选D.
10.A.∵EF∥AB,∴=,故本选项正确,
B.∵DE∥BC,
∴=,
∵EF∥AB,
∴DE=BF,
∴=,
∴=,
故本选项正确,
C.∵EF∥AB,
∴=,
∵CF≠DE,
∴≠,
故本选项错误,
D.∵EF∥AB,
∴=,
∴=,
故本选项正确,
故选:C.
二.填空题(共9小题,满分36分)
11.解:两边都减2,得
==,
故答案为:.
12.解:由于P为线段AB=8cm的黄金分割点,
则AP=8×=4﹣4,
或AP=8﹣(4﹣4)=12﹣4.
故本题答案为:4﹣4或12﹣4.
13.解:∵DE∥BC,
∴=,
又AE:EC=2:3,即AE:AC=2:5,
∴DE:BC=2:5.
故答案为:2:5.
14.解:分两种情况:
①当a+b+c=0时,则有a+b=﹣c,
所以k===﹣2;
②当a+b+c≠0时,
∵,
∴k==1.
故答案为﹣2或1.
15.解:设A,B两地的实际距离为xkm,则:
=,解得x=32000000cm=320km,
∴两地间的实际距离是320km.
16.解:作DF∥BE交AC于F,
∵AD是△ABC的中线,
∴EF=FC=EC,
∵AE:EC=1:3,设AE=x,EC=3x,
∴EF=1.5x.
∵DF∥BE,
∴△AGE∽△ADF,
∴,
∴,
∴.
故答案为:2:3.
17.解:∵=,=,
∴=,
∴a:b:c=9:12:20.
故填9:12:20.
18.解:∵四边形ABCD是梯形,
∴AD∥BC;
又EF∥BC,
∴AD∥EF∥BC,
∴=(平行线分线段成比例);
∵,
∴=,
∴=(等量代换).
故答案是:.
三.解答题(共7小题,满分40分)
19.证明:如图,
过B作BE∥AC,交AD的延长线交于E.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵BE∥AC,
∴∠CAD=∠E.
∴∠BAD=∠E,
∴AB=BE.
又∵BE∥AC,
∴△BDE∽△CDA,
∴BE:AC=BD:DC,
∴.
20.解:∵l1∥l2∥l3,
∴==,
即,
解得:EF=4.5,
∴DF=DE+EF=6+4.5=10.5.
21.解:由x:y:z=7:5:3,得
x=7a,y=5a,z=3a.
由x+y=24得
7a+5a=24.
解得a=2,
x=7a=14,y=5a=10,z=3a=6.
22.解:∵DE∥BC,
∴==,又BC=40,
∴DE=16,
∵DE∥BC,EF∥AB,
∴四边形DBFE是平行四边形,
∴BF=DE=16,
∴CF=BC﹣BF=24.
23.解:①当x+y+z≠0时,由等比性质,得
==.
由反比性质,得
∴==2.
②当x+y+z=0时,=﹣1.
24.解:∵D在AB上,且AD2=BD AB,
∴点D是AB的黄金分割点,且AD=AB=﹣1,
而点C是AB的黄金分割点,
当C、D重合时,=0,
当C、D不重合时,AC=3﹣,
∴CD=﹣1﹣(3﹣)=2﹣4,
∴==.
