2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用解答题专题训练(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用解答题专题训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 709.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 12:28:07 | ||
图片预览


文档简介
2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》
解答题专题训练(附答案)
1.如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
2.如图,一艘货船在灯塔C的正南方向,距离灯塔257海里的A处遇险,发出求救信号.一艘救生船位于灯塔C的南偏东40°方向上,同时位于A处的北偏东60°方向上的B处,救生船接到求救信号后,立即前往救援.求AB的长.(结果取整数)参考数据:tan40°≈0.84,取1.73.
3.一座吊桥的钢索立柱AD两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索AB的长度.他们测得∠ABD为30°,由于B、D两点间的距离不易测得,通过探究和测量,发现∠ACD恰好为45°,点B与点C之间的距离约为16m.已知B、C、D共线,AD⊥BD.求钢索AB的长度.(结果保留根号)
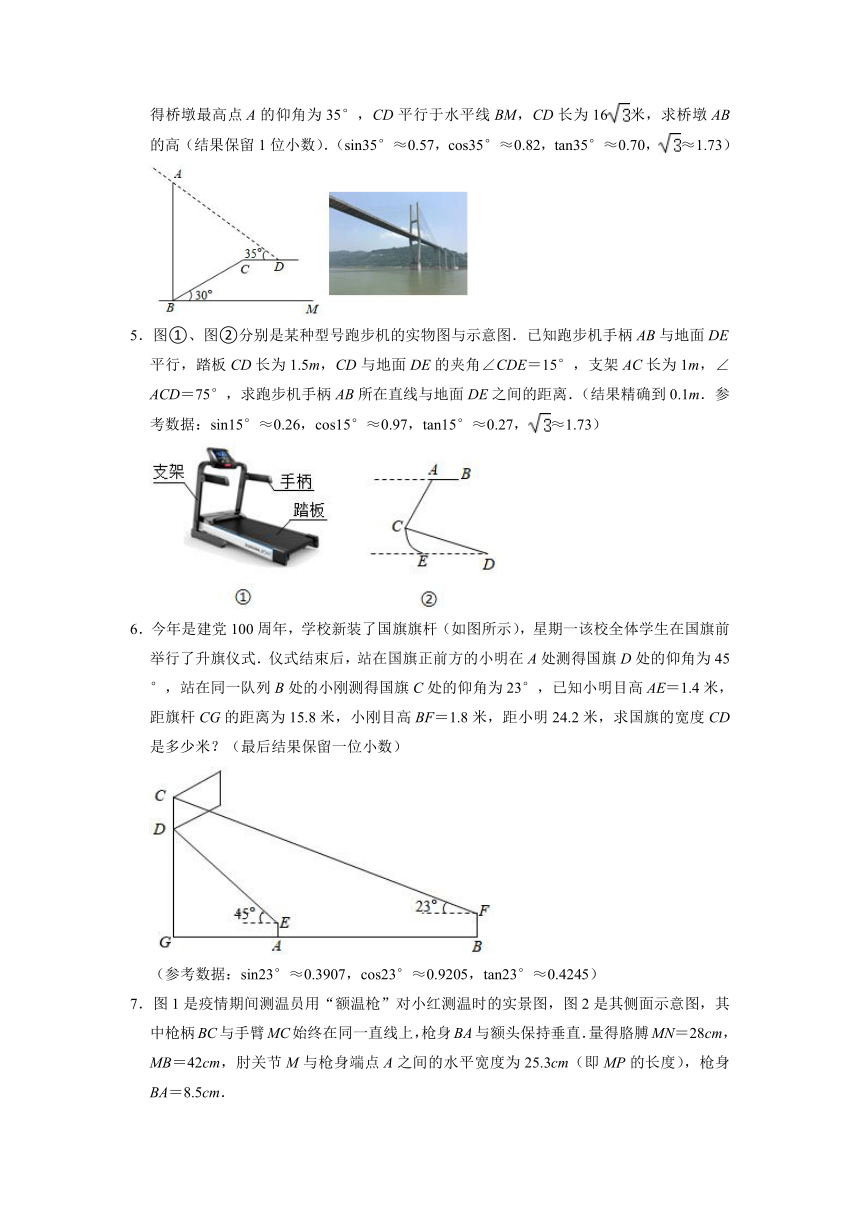
4.2021年,州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为30°的河床斜坡边,斜坡BC长为48米,在点D处测得桥墩最高点A的仰角为35°,CD平行于水平线BM,CD长为16米,求桥墩AB的高(结果保留1位小数).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,≈1.73)
5.图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE平行,踏板CD长为1.5m,CD与地面DE的夹角∠CDE=15°,支架AC长为1m,∠ACD=75°,求跑步机手柄AB所在直线与地面DE之间的距离.(结果精确到0.1m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.73)
6.今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为45°,站在同一队列B处的小刚测得国旗C处的仰角为23°,已知小明目高AE=1.4米,距旗杆CG的距离为15.8米,小刚目高BF=1.8米,距小明24.2米,求国旗的宽度CD是多少米?(最后结果保留一位小数)
(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245)
7.图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.
(1)求∠ABC的度数;
(2)测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)
(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,≈1.414)
8.如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
9.如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:
方案设计:如图2,宝塔CD垂直于地面,在地面上选取A,B两处分别测得∠CAD和∠CBD的度数(A,D,B在同一条直线上).
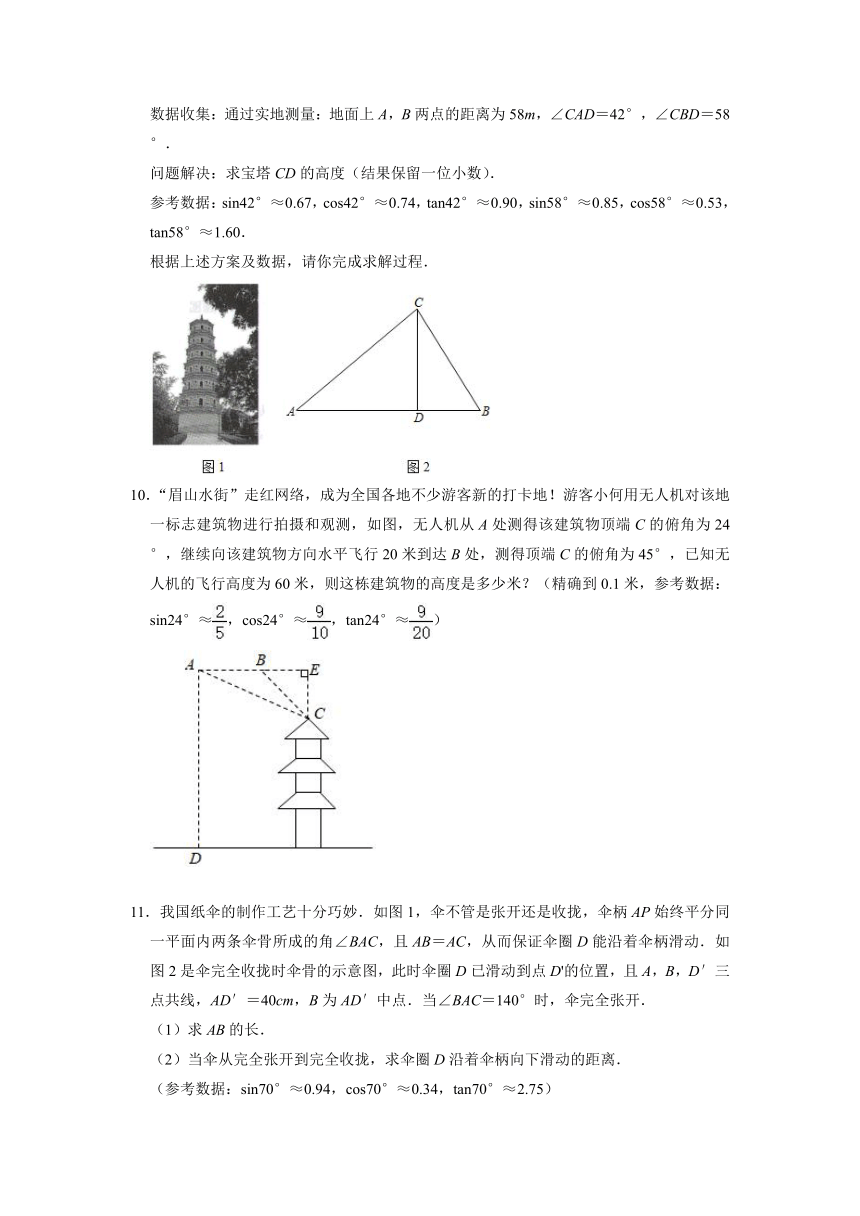
数据收集:通过实地测量:地面上A,B两点的距离为58m,∠CAD=42°,∠CBD=58°.
问题解决:求宝塔CD的高度(结果保留一位小数).
参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60.
根据上述方案及数据,请你完成求解过程.
10.“眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从A处测得该建筑物顶端C的俯角为24°,继续向该建筑物方向水平飞行20米到达B处,测得顶端C的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据:sin24°≈,cos24°≈,tan24°≈)
11.我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,且AB=AC,从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点D'的位置,且A,B,D′三点共线,AD′=40cm,B为AD′中点.当∠BAC=140°时,伞完全张开.
(1)求AB的长.
(2)当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.
(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
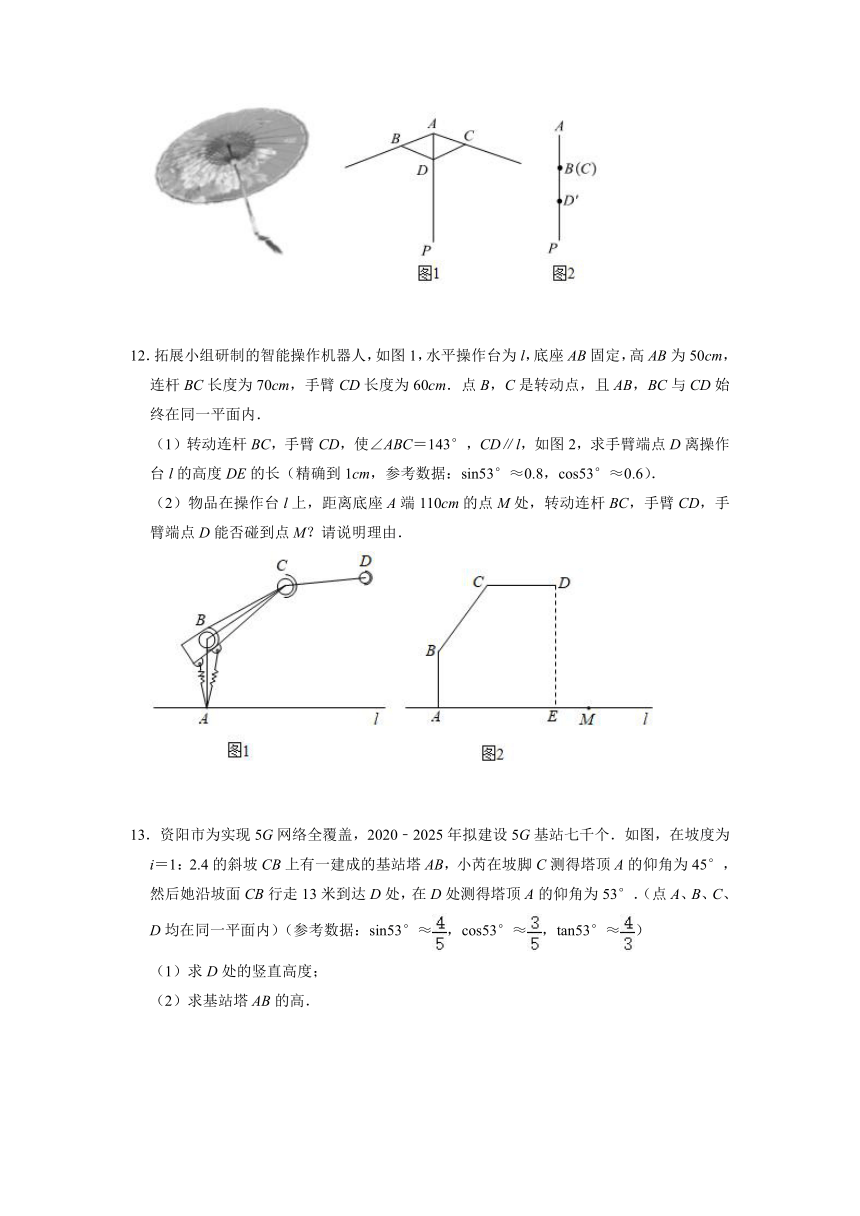
12.拓展小组研制的智能操作机器人,如图1,水平操作台为l,底座AB固定,高AB为50cm,连杆BC长度为70cm,手臂CD长度为60cm.点B,C是转动点,且AB,BC与CD始终在同一平面内.
(1)转动连杆BC,手臂CD,使∠ABC=143°,CD∥l,如图2,求手臂端点D离操作台l的高度DE的长(精确到1cm,参考数据:sin53°≈0.8,cos53°≈0.6).
(2)物品在操作台l上,距离底座A端110cm的点M处,转动连杆BC,手臂CD,手臂端点D能否碰到点M?请说明理由.
13.资阳市为实现5G网络全覆盖,2020﹣2025年拟建设5G基站七千个.如图,在坡度为i=1:2.4的斜坡CB上有一建成的基站塔AB,小芮在坡脚C测得塔顶A的仰角为45°,然后她沿坡面CB行走13米到达D处,在D处测得塔顶A的仰角为53°.(点A、B、C、D均在同一平面内)(参考数据:sin53°≈,cos53°≈,tan53°≈)
(1)求D处的竖直高度;
(2)求基站塔AB的高.
14.一酒精消毒瓶如图1,AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=6cm,BE=4cm.当按压柄△BCD按压到底时,BD转动到BD′,此时BD′∥EF(如图3).
(1)求点D转动到点D′的路径长;
(2)求点D到直线EF的距离(结果精确到0.1cm).
(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
15.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走2米到达斜坡上D点,在点D处测得树顶端A的仰角为30°,若斜坡CF的坡比为i=1:3(点E、C、B在同一水平线上).
(1)求王刚同学从点C到点D的过程中上升的高度;
(2)求大树AB的高度(结果保留根号).
16.越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角∠MBC=33°,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角∠MEC=45°(点A,D与N在一条直线上),求电池板离地面的高度MN的长.(结果精确到1米;参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)
17.学生到工厂劳动实践,学习制作机械零件.零件的截面如图阴影部分所示,已知四边形AEFD为矩形,点B、C分别在EF、DF上,∠ABC=90°,∠BAD=53°,AB=10cm,BC=6cm.求零件的截面面积.参考数据:sin53°≈0.80,cos53°≈0.60.
18.我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿AB摆成如图1所示.已知AB=4.8m,鱼竿尾端A离岸边0.4m,即AD=0.4m.海面与地面AD平行且相距1.2m,即DH=1.2m.
(1)如图1,在无鱼上钩时,海面上方的鱼线BC与海面HC的夹角∠BCH=37°,海面下方的鱼线CO与海面HC垂直,鱼竿AB与地面AD的夹角∠BAD=22°.求点O到岸边DH的距离;
(2)如图2,在有鱼上钩时,鱼竿与地面的夹角∠BAD=53°,此时鱼线被拉直,鱼线BO=5.46m,点O恰好位于海面.求点O到岸边DH的距离.
(参考数据:sin37°=cos53°≈,cos37°=sin53°≈,tan37°≈,sin22°≈,cos22°≈,tan22°≈)
19.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)求∠C的度数;
(2)求两棵银杏树B、C之间的距离(结果保留根号).
20.在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度.(结果精确到0.1,参考数据tan37°≈0.75,tan53°≈1.33,≈1.73)
21.如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C点处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,且测得C点与观测点A的距离为25海里.
(1)求观测点B与C点之间的距离;
(2)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.
参考答案
1.解:(1)∵AC⊥BD,cos∠ABC==,BC=8,
∴AB=10,
在Rt△ACB中,由勾股定理得,
AC===6,
即AC的长为6;
(2)如图,
连接CF,过F点作BD的垂线,垂足E,
∵BF为AD边上的中线,
即F为AD的中点,
∴CF=AD=FD,
在Rt△ACD中,由勾股定理得,
AD===2,
∵三角形CFD为等腰三角形,FE⊥CD,
∴CE=CD=2,
在Rt△EFC中,EF===3,
∴tan∠FBD===.
解法二:∵BF为AD边上的中线,
∴F是AD中点,
∵FE⊥BD,AC⊥BD,
∴FE∥AC,
∴FE是△ACD的中位线,
∴FE=AC=3,CE=CD=2,
∴在Rt△BFE中,tan∠FBD===.
2.解:如图,过点B作BH⊥AC,垂足为H,
由题意得,∠BAC=60°,∠BCA=40°,AC=257海里,
在Rt△ABH中,
∵tan∠BAH=,cos∠BAH=,
∴BH=AH tan60°=AH,AB==2AH,
在Rt△BCH中,
∵tan∠BCH=,
∴CH==(海里),
又∵CA=CH+AH,
∴257=+AH,
所以AH=(海里),
∴AB=≈=168(海里),
答:AB的长约为168海里.
3.解:在△ADC中,设AD=xm,
∵AD⊥BD,∠ACD=45°,
∴CD=AD=xm,
在△ADB中,AD⊥BD,∠ABD=30°,
∴AD=BD tan30°,
即x=(16+x)m,
解得:x=(8+8)m,
∴AB=2AD=2×(8)=(16)m,
∴钢索AB的长度为(16)m.
4.解:过点C作CE⊥BM于点E,过点D作DF⊥BM于点F,延长DC交AB于点G,
在Rt△CEB中,∠CBE=30°,BC=48米,
∴CE=BC sin30°=×48=24(米),BE=BC cos30°=48×≈24×1.73=41.52(米),
∴DG=BF=BE+EF=BE+CD=41.52+16≈41.52+27.68=69.2(米),
在Rt△ADG中,AG=DG tan∠ADG=69.2×tan35°≈69.2×0.70=48.44(米),
∴AB=AG+BG=AG+CE=48.44+24=72.44≈72.4(米),
答:桥墩AB的高约为72.4米.
5.解:如图,过C点作FG⊥AB于F,交DE于G.
∵CD与地面DE的夹角∠CDE为15°,∠ACD为75°,
∴∠ACF=∠FCD﹣∠ACD=∠CGD+∠CDE﹣∠ACD=90°+15°﹣75°=30°,
∴∠CAF=60°,
在Rt△ACF中,CF=AC sin∠CAF=m,
在Rt△CDG中,CG=CD sin∠CDE=1.5 sin15°m,
∴FG=FC+CG=+1.5 sin15°≈1.3m.
故跑步机手柄AB所在直线与地面DE之间的距离约为1.3m.
6.解:作EM⊥CG于M,FN⊥CG于N,
由题意得GB=AG+AB=15.8+24.2=40(米),
则FN=GB=40米,
在Rt△EDM中,∠DEM=45°,
∴DM=EM=15.8米,
∵MG=AE=1.4米,
∴DG=DM+MG=15.8+1.4=17.2(米),
∵NG=FB=1.8米,
∴DN=17.2﹣1.8=15.4(米),
在Rt△CNF中,∠CFN=23°,
∵tan∠CFN=≈0.4245,
∴CN=0.4245×40≈17.0(米),
∴CD=CN﹣DN=17.0﹣15.4=1.6(米)
故国旗的宽度CD约为1.6米.
7.解:(1)过点B作BH⊥MP,垂足为H,过点M作MI⊥FG,垂足为I,过点P作PK⊥DE,垂足为K,
∵MP=25.3cm,BA=HP=8.5cm,
∴MH=MP﹣HP=25.3﹣8.5=16.8(cm),
在Rt△BMH中,
cos∠BMH===0.4,
∴∠BMH=66.4°,
∵AB∥MP,
∴∠BMH+∠ABC=180°,
∴∠ABC=180°﹣66.4°=113.6°;
(2)∵∠BMN=68.6°,∠BMH=66.4°,
∴∠NMI=180°﹣∠BMN﹣∠BMH=180°﹣68.6°﹣66.4°=45°,
∵MN=28cm,
∴cos45°==,
∴MI≈19.80cm,
∵KI=50cm,
∴PK=KI﹣MI﹣MP=50﹣19.80﹣25.3=4.90≈4.9(cm),
∴此时枪身端点A与小红额头的距离是在规定范围内.
8.解:∵CM=3m,OC=5m,
∴OM==4(m),
∵∠CMO=∠BDO=90°,∠COM=∠BOD,
∴△COM∽△BOD,
∴,即,
∴BD==2.25(m),
∴tan∠AOD=tan70°=,
即≈2.75,
解得:AB=6m,
∴汽车从A处前行约6米才能发现C处的儿童.
9.解:设CD=xm,
在Rt△ACD中,AD=,
在Rt△BCD中,BD=,
∵AD+BD=AB,
∴,
解得,x≈33.4.
答:宝塔的高度约为33.4m.
10.解:过C作CF⊥AD于F,如图所示:
则AF=CE,
由题意得:AB=20米,∠AEC=90°,∠CAE=24°,∠CBE=45°,
∴△BCE是等腰直角三角形,
∴BE=CE,
设BE=CE=x米,则AF=x米,
在Rt△ACE中,tan∠CAE==tan24°≈,
∴AE=x米,
∵AE﹣BE=AB,
∴x﹣x=20,
解得:x≈16.4,
∴AF≈16.4(米),
∴DF=AD﹣AF=60﹣16.4=43.6(米),
即这栋建筑物的高度为43.6米.
11.解:(1)∵B为AD′中点,
∴AB=AD′,
∵AD′=40cm,
∴AB=20cm;
(2)如图,过点B作BE⊥AD于点E,
∵AB=BD,
∴AD=2AE,
∵AP平分∠BAC,∠BAC=140°,
∴∠BAE=BAC=70°,
在Rt△ABE中,AB=20cm
∴AE=AB cos70°≈20×0.34=6.8(cm),
∴AD=2AE=13.6(cm),
∵AD′=40cm,
∴40﹣13.6=26.4(cm).
∴伞圈D沿着伞柄向下滑动的距离为26.4cm.
12.解:(1)过点C作CP⊥AE于点P,过点B作BQ⊥CP于点Q,如图:
∵∠ABC=143°,
∴∠CBQ=53°,
在Rt△BCQ中,CQ=BC sin53°≈70×0.8=56cm,
∵CD∥l,
∴DE=CP=CQ+PQ=56+50=106cm.
(2)手臂端点D能碰到点M,
理由:由题意得,当B,C,D共线时,手臂端点D能碰到最远距离,
如图:
BD=60+70=130cm,AB=50cm,
在Rt△ABD中,AB +AD =BD ,
∴AD=120cm>110cm.
∴手臂端点D能碰到点M.
13.解:(1)如图,过点C、D分别作AB的垂线,交AB的延长线于点E、F,过点D作DM⊥CF,垂足为M,
∵斜坡CB的坡度为i=1:2.4,
∴=,
即=,
设DM=5k米,则CM=12k米,
在Rt△CDM中,CD=13米,由勾股定理得,
CM2+DM2=CD2,
即(5k)2+(12k)2=132,
解得k=1,
∴DM=5(米),CM=12(米),
答:D处的竖直高度为5米;
(2)斜坡CB的坡度为i=1:2.4,
设DE=12a米,则BE=5a米,
又∵∠ACF=45°,
∴AF=CF=(12+12a)米,
∴AE=AF﹣EF=12+12a﹣5=(7+12a)米,
在Rt△ADE中,DE=12a米,AE=(7+12a)米,
∵tan∠ADE=tan53°≈,
∴=,
解得a=,
∴DE=12a=21(米),AE=7+12a=28(米),
BE=5a=(米),
∴AB=AE﹣BE=28﹣=(米),
答:基站塔AB的高为米.
14.解:∵BD'∥EF,∠BEF=108°,
∴∠D'BE=180°﹣∠BEF=72°,
∵∠DBE=108°,
∴∠DBD'=∠DBE﹣∠D'BE=108°﹣72°=36°,
∵BD=6,
∴点D转动到点D′的路径长为=π(cm);
(2)过D作DG⊥BD'于G,过E作EH⊥BD'于H,如图:
Rt△BDG中,DG=BD sin36°≈6×0.59=3.54(cm),
Rt△BEH中,HE=BE sin72°≈4×0.95=3.80(cm),
∴DG+HE=3.54cm+3.80cm=7.34m≈7.3cm,
∵BD'∥EF,
∴点D到直线EF的距离约为7.3cm,
答:点D到直线EF的距离约为7.3cm.
15.解:(1)过点D作DH⊥CE于点H,
由题意知CD=2米,
∵斜坡CF的坡比为i=1:3,
∴,
设DH=x米,CH=3x米,
∵DH2+CH2=DC2,
∴,
∴x=2,
∴DH=2(米),CH=6(米),
答:王刚同学从点C到点D的过程中上升的高度为2米;
(2)过点D作DG⊥AB于点G,设BC=a米,
∵∠DHB=∠DGB=∠ABC=90°,
∴四边形DHBG为矩形,
∴DH=BG=2米,DG=BH=(a+6)米,
∵∠ACB=45°,
∴BC=AB=a(米),
∴AG=(a﹣2)米,
∵∠ADG=30°,
∴,
∴,
∴a=6+4,
∴AB=(6+4)(米).
答:大树AB的高度是(6+4)米.
16.解:延长BC交MN于点H,AD=BE=3.5,
设MH=x米,
∵∠MEC=45°,
∴EH=x米,
在Rt△MHB中,tan∠MBH==≈0.65,解得x=6.5,
则MN=1.6+6.5=8.1≈8(米),
∴电池板离地面的高度MN的长约为8米.
17.解:如图,
∵四边形AEFD为矩形,∠BAD=53°,
∴AD∥EF,∠E=∠F=90°,
∴∠BAD=∠EBA=53°,
在Rt△ABE中,∠E=90°,AB=10cm,∠EBA=53°,
∴sin∠EBA=≈0.80,cos∠EBA=≈0.60,
∴AE=8cm,BE=6cm,
∵∠ABC=90°,
∴∠FBC=90°﹣∠EBA=37°,
∴∠BCF=90°﹣∠FBC=53°,
在Rt△BCF中,∠F=90°,BC=6cm,
∴sin∠BCF=≈0.80,cos∠BCF=≈0.60,
∴BF=4.8cm,FC=3.6cm,
∴EF=6+4.8=10.8cm,
∴S四边形EFDA=AE EF=8×10.8=86.4(cm2),
S△ABE==×8×6=24(cm2),
S△BCF= BF CF=×4.8×3.6=8.64(cm2),
∴截面的面积=S四边形EFDA﹣S△ABE﹣S△BCF=86.4﹣24﹣8.64=53.76(cm2).
18.解:(1)过点B作BF⊥CH,垂足为F,延长AD交BF于E,垂足为E,则AE⊥BF,
由cos∠BAE=,
∴cos22°=,
∴,即AE=4.5m,
∴DE=AE﹣AD=4.5﹣0.4=4.1(m),
由sin∠BAE=,
∴,
∴,即BE=1.8m,
∴BF=BE+EF=1.8+1.2=3(m),
又,
∴,即CF=4m,
∴CH=CF+HF=CF+DE=4+4.1=8.1(m),即点O到岸边DH的距离为8.1m;
(2)过点B作BN⊥OH,垂足为N,延长AD交BN于点M,垂足为M,
由cos∠BAM=,
∴,
∴,
即AM=2.88m,
∴DM=AM﹣AD=2.88﹣0.4=2.48(m),
由sin∠BAM=,
∴,
∴,即BM=3.84m,
∴BN=BM+MN=3.84+1.2=5.04(m),
∴=(m),
∴OH=ON+HN=ON+DM=4.58(m),
即点O到岸边的距离为4.58m.
19.解:(1)设AD与BC交于点F,
由题意得BE∥AD,
∵BE∥AD且∠EBF=60°,
∴∠BFA=∠EBF=60°,
∵∠BFA=∠C+∠CAD且∠CAD=30°,
∴∠C=∠BFA﹣∠CAD=30°;
(2)过点B作BG⊥AD于G.
∵BG⊥AD,
∴∠AGB=∠BGD=90°,
在Rt△AGB中,AB=20米,∠BAG=45°,
AG=BG=20×sin45°=(米),
在Rt△BGF中,∠BFG=60°,
∴BF===(米),FG=BGtan60°===(米),
∵∠C=∠CAD=30°,
∴CF=AF=AG+FG=(10+)(米),
∴BC=BF+CF=(10+10)米,
答:两棵银杏树B、C之间的距离为(10+10)米.
20.解:由题意可知AB=24米,∠BDA=53°,
∴tan∠BDA==≈1.33,
∴AD=≈18.05(米).
∵tan∠CAD=tan30°===,
∴CD=18.05×≈10.4(米).
故办公楼的高度约为10.4米.
21.解:(1)如图,过点C作CE⊥AB于点E,
根据题意可知:∠ACE=∠CAE=45°,AC=25海里,
∴AE=CE=25(海里),
∵∠CBE=30°,
∴BE=25(海里),
∴BC=2CE=50(海里).
答:观测点B与C点之间的距离为50海里;
(2)如图,作CF⊥DB于点F,
∵CF⊥DB,FB⊥EB,CE⊥AB,
∴四边形CEBF是矩形,
∴FB=CE=25(海里),CF=BE=25(海里),
∴DF=BD+BF=30+25=55(海里),
在Rt△DCF中,根据勾股定理,得
CD===70(海里),
∴70÷42=(小时).
答:救援船到达C点需要的最少时间是小时.
解答题专题训练(附答案)
1.如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
2.如图,一艘货船在灯塔C的正南方向,距离灯塔257海里的A处遇险,发出求救信号.一艘救生船位于灯塔C的南偏东40°方向上,同时位于A处的北偏东60°方向上的B处,救生船接到求救信号后,立即前往救援.求AB的长.(结果取整数)参考数据:tan40°≈0.84,取1.73.
3.一座吊桥的钢索立柱AD两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索AB的长度.他们测得∠ABD为30°,由于B、D两点间的距离不易测得,通过探究和测量,发现∠ACD恰好为45°,点B与点C之间的距离约为16m.已知B、C、D共线,AD⊥BD.求钢索AB的长度.(结果保留根号)
4.2021年,州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为30°的河床斜坡边,斜坡BC长为48米,在点D处测得桥墩最高点A的仰角为35°,CD平行于水平线BM,CD长为16米,求桥墩AB的高(结果保留1位小数).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,≈1.73)
5.图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE平行,踏板CD长为1.5m,CD与地面DE的夹角∠CDE=15°,支架AC长为1m,∠ACD=75°,求跑步机手柄AB所在直线与地面DE之间的距离.(结果精确到0.1m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.73)
6.今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为45°,站在同一队列B处的小刚测得国旗C处的仰角为23°,已知小明目高AE=1.4米,距旗杆CG的距离为15.8米,小刚目高BF=1.8米,距小明24.2米,求国旗的宽度CD是多少米?(最后结果保留一位小数)
(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245)
7.图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.
(1)求∠ABC的度数;
(2)测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)
(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,≈1.414)
8.如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
9.如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:
方案设计:如图2,宝塔CD垂直于地面,在地面上选取A,B两处分别测得∠CAD和∠CBD的度数(A,D,B在同一条直线上).
数据收集:通过实地测量:地面上A,B两点的距离为58m,∠CAD=42°,∠CBD=58°.
问题解决:求宝塔CD的高度(结果保留一位小数).
参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60.
根据上述方案及数据,请你完成求解过程.
10.“眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从A处测得该建筑物顶端C的俯角为24°,继续向该建筑物方向水平飞行20米到达B处,测得顶端C的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据:sin24°≈,cos24°≈,tan24°≈)
11.我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,且AB=AC,从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点D'的位置,且A,B,D′三点共线,AD′=40cm,B为AD′中点.当∠BAC=140°时,伞完全张开.
(1)求AB的长.
(2)当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.
(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
12.拓展小组研制的智能操作机器人,如图1,水平操作台为l,底座AB固定,高AB为50cm,连杆BC长度为70cm,手臂CD长度为60cm.点B,C是转动点,且AB,BC与CD始终在同一平面内.
(1)转动连杆BC,手臂CD,使∠ABC=143°,CD∥l,如图2,求手臂端点D离操作台l的高度DE的长(精确到1cm,参考数据:sin53°≈0.8,cos53°≈0.6).
(2)物品在操作台l上,距离底座A端110cm的点M处,转动连杆BC,手臂CD,手臂端点D能否碰到点M?请说明理由.
13.资阳市为实现5G网络全覆盖,2020﹣2025年拟建设5G基站七千个.如图,在坡度为i=1:2.4的斜坡CB上有一建成的基站塔AB,小芮在坡脚C测得塔顶A的仰角为45°,然后她沿坡面CB行走13米到达D处,在D处测得塔顶A的仰角为53°.(点A、B、C、D均在同一平面内)(参考数据:sin53°≈,cos53°≈,tan53°≈)
(1)求D处的竖直高度;
(2)求基站塔AB的高.
14.一酒精消毒瓶如图1,AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=6cm,BE=4cm.当按压柄△BCD按压到底时,BD转动到BD′,此时BD′∥EF(如图3).
(1)求点D转动到点D′的路径长;
(2)求点D到直线EF的距离(结果精确到0.1cm).
(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
15.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走2米到达斜坡上D点,在点D处测得树顶端A的仰角为30°,若斜坡CF的坡比为i=1:3(点E、C、B在同一水平线上).
(1)求王刚同学从点C到点D的过程中上升的高度;
(2)求大树AB的高度(结果保留根号).
16.越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角∠MBC=33°,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角∠MEC=45°(点A,D与N在一条直线上),求电池板离地面的高度MN的长.(结果精确到1米;参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)
17.学生到工厂劳动实践,学习制作机械零件.零件的截面如图阴影部分所示,已知四边形AEFD为矩形,点B、C分别在EF、DF上,∠ABC=90°,∠BAD=53°,AB=10cm,BC=6cm.求零件的截面面积.参考数据:sin53°≈0.80,cos53°≈0.60.
18.我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿AB摆成如图1所示.已知AB=4.8m,鱼竿尾端A离岸边0.4m,即AD=0.4m.海面与地面AD平行且相距1.2m,即DH=1.2m.
(1)如图1,在无鱼上钩时,海面上方的鱼线BC与海面HC的夹角∠BCH=37°,海面下方的鱼线CO与海面HC垂直,鱼竿AB与地面AD的夹角∠BAD=22°.求点O到岸边DH的距离;
(2)如图2,在有鱼上钩时,鱼竿与地面的夹角∠BAD=53°,此时鱼线被拉直,鱼线BO=5.46m,点O恰好位于海面.求点O到岸边DH的距离.
(参考数据:sin37°=cos53°≈,cos37°=sin53°≈,tan37°≈,sin22°≈,cos22°≈,tan22°≈)
19.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)求∠C的度数;
(2)求两棵银杏树B、C之间的距离(结果保留根号).
20.在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度.(结果精确到0.1,参考数据tan37°≈0.75,tan53°≈1.33,≈1.73)
21.如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C点处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,且测得C点与观测点A的距离为25海里.
(1)求观测点B与C点之间的距离;
(2)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.
参考答案
1.解:(1)∵AC⊥BD,cos∠ABC==,BC=8,
∴AB=10,
在Rt△ACB中,由勾股定理得,
AC===6,
即AC的长为6;
(2)如图,
连接CF,过F点作BD的垂线,垂足E,
∵BF为AD边上的中线,
即F为AD的中点,
∴CF=AD=FD,
在Rt△ACD中,由勾股定理得,
AD===2,
∵三角形CFD为等腰三角形,FE⊥CD,
∴CE=CD=2,
在Rt△EFC中,EF===3,
∴tan∠FBD===.
解法二:∵BF为AD边上的中线,
∴F是AD中点,
∵FE⊥BD,AC⊥BD,
∴FE∥AC,
∴FE是△ACD的中位线,
∴FE=AC=3,CE=CD=2,
∴在Rt△BFE中,tan∠FBD===.
2.解:如图,过点B作BH⊥AC,垂足为H,
由题意得,∠BAC=60°,∠BCA=40°,AC=257海里,
在Rt△ABH中,
∵tan∠BAH=,cos∠BAH=,
∴BH=AH tan60°=AH,AB==2AH,
在Rt△BCH中,
∵tan∠BCH=,
∴CH==(海里),
又∵CA=CH+AH,
∴257=+AH,
所以AH=(海里),
∴AB=≈=168(海里),
答:AB的长约为168海里.
3.解:在△ADC中,设AD=xm,
∵AD⊥BD,∠ACD=45°,
∴CD=AD=xm,
在△ADB中,AD⊥BD,∠ABD=30°,
∴AD=BD tan30°,
即x=(16+x)m,
解得:x=(8+8)m,
∴AB=2AD=2×(8)=(16)m,
∴钢索AB的长度为(16)m.
4.解:过点C作CE⊥BM于点E,过点D作DF⊥BM于点F,延长DC交AB于点G,
在Rt△CEB中,∠CBE=30°,BC=48米,
∴CE=BC sin30°=×48=24(米),BE=BC cos30°=48×≈24×1.73=41.52(米),
∴DG=BF=BE+EF=BE+CD=41.52+16≈41.52+27.68=69.2(米),
在Rt△ADG中,AG=DG tan∠ADG=69.2×tan35°≈69.2×0.70=48.44(米),
∴AB=AG+BG=AG+CE=48.44+24=72.44≈72.4(米),
答:桥墩AB的高约为72.4米.
5.解:如图,过C点作FG⊥AB于F,交DE于G.
∵CD与地面DE的夹角∠CDE为15°,∠ACD为75°,
∴∠ACF=∠FCD﹣∠ACD=∠CGD+∠CDE﹣∠ACD=90°+15°﹣75°=30°,
∴∠CAF=60°,
在Rt△ACF中,CF=AC sin∠CAF=m,
在Rt△CDG中,CG=CD sin∠CDE=1.5 sin15°m,
∴FG=FC+CG=+1.5 sin15°≈1.3m.
故跑步机手柄AB所在直线与地面DE之间的距离约为1.3m.
6.解:作EM⊥CG于M,FN⊥CG于N,
由题意得GB=AG+AB=15.8+24.2=40(米),
则FN=GB=40米,
在Rt△EDM中,∠DEM=45°,
∴DM=EM=15.8米,
∵MG=AE=1.4米,
∴DG=DM+MG=15.8+1.4=17.2(米),
∵NG=FB=1.8米,
∴DN=17.2﹣1.8=15.4(米),
在Rt△CNF中,∠CFN=23°,
∵tan∠CFN=≈0.4245,
∴CN=0.4245×40≈17.0(米),
∴CD=CN﹣DN=17.0﹣15.4=1.6(米)
故国旗的宽度CD约为1.6米.
7.解:(1)过点B作BH⊥MP,垂足为H,过点M作MI⊥FG,垂足为I,过点P作PK⊥DE,垂足为K,
∵MP=25.3cm,BA=HP=8.5cm,
∴MH=MP﹣HP=25.3﹣8.5=16.8(cm),
在Rt△BMH中,
cos∠BMH===0.4,
∴∠BMH=66.4°,
∵AB∥MP,
∴∠BMH+∠ABC=180°,
∴∠ABC=180°﹣66.4°=113.6°;
(2)∵∠BMN=68.6°,∠BMH=66.4°,
∴∠NMI=180°﹣∠BMN﹣∠BMH=180°﹣68.6°﹣66.4°=45°,
∵MN=28cm,
∴cos45°==,
∴MI≈19.80cm,
∵KI=50cm,
∴PK=KI﹣MI﹣MP=50﹣19.80﹣25.3=4.90≈4.9(cm),
∴此时枪身端点A与小红额头的距离是在规定范围内.
8.解:∵CM=3m,OC=5m,
∴OM==4(m),
∵∠CMO=∠BDO=90°,∠COM=∠BOD,
∴△COM∽△BOD,
∴,即,
∴BD==2.25(m),
∴tan∠AOD=tan70°=,
即≈2.75,
解得:AB=6m,
∴汽车从A处前行约6米才能发现C处的儿童.
9.解:设CD=xm,
在Rt△ACD中,AD=,
在Rt△BCD中,BD=,
∵AD+BD=AB,
∴,
解得,x≈33.4.
答:宝塔的高度约为33.4m.
10.解:过C作CF⊥AD于F,如图所示:
则AF=CE,
由题意得:AB=20米,∠AEC=90°,∠CAE=24°,∠CBE=45°,
∴△BCE是等腰直角三角形,
∴BE=CE,
设BE=CE=x米,则AF=x米,
在Rt△ACE中,tan∠CAE==tan24°≈,
∴AE=x米,
∵AE﹣BE=AB,
∴x﹣x=20,
解得:x≈16.4,
∴AF≈16.4(米),
∴DF=AD﹣AF=60﹣16.4=43.6(米),
即这栋建筑物的高度为43.6米.
11.解:(1)∵B为AD′中点,
∴AB=AD′,
∵AD′=40cm,
∴AB=20cm;
(2)如图,过点B作BE⊥AD于点E,
∵AB=BD,
∴AD=2AE,
∵AP平分∠BAC,∠BAC=140°,
∴∠BAE=BAC=70°,
在Rt△ABE中,AB=20cm
∴AE=AB cos70°≈20×0.34=6.8(cm),
∴AD=2AE=13.6(cm),
∵AD′=40cm,
∴40﹣13.6=26.4(cm).
∴伞圈D沿着伞柄向下滑动的距离为26.4cm.
12.解:(1)过点C作CP⊥AE于点P,过点B作BQ⊥CP于点Q,如图:
∵∠ABC=143°,
∴∠CBQ=53°,
在Rt△BCQ中,CQ=BC sin53°≈70×0.8=56cm,
∵CD∥l,
∴DE=CP=CQ+PQ=56+50=106cm.
(2)手臂端点D能碰到点M,
理由:由题意得,当B,C,D共线时,手臂端点D能碰到最远距离,
如图:
BD=60+70=130cm,AB=50cm,
在Rt△ABD中,AB +AD =BD ,
∴AD=120cm>110cm.
∴手臂端点D能碰到点M.
13.解:(1)如图,过点C、D分别作AB的垂线,交AB的延长线于点E、F,过点D作DM⊥CF,垂足为M,
∵斜坡CB的坡度为i=1:2.4,
∴=,
即=,
设DM=5k米,则CM=12k米,
在Rt△CDM中,CD=13米,由勾股定理得,
CM2+DM2=CD2,
即(5k)2+(12k)2=132,
解得k=1,
∴DM=5(米),CM=12(米),
答:D处的竖直高度为5米;
(2)斜坡CB的坡度为i=1:2.4,
设DE=12a米,则BE=5a米,
又∵∠ACF=45°,
∴AF=CF=(12+12a)米,
∴AE=AF﹣EF=12+12a﹣5=(7+12a)米,
在Rt△ADE中,DE=12a米,AE=(7+12a)米,
∵tan∠ADE=tan53°≈,
∴=,
解得a=,
∴DE=12a=21(米),AE=7+12a=28(米),
BE=5a=(米),
∴AB=AE﹣BE=28﹣=(米),
答:基站塔AB的高为米.
14.解:∵BD'∥EF,∠BEF=108°,
∴∠D'BE=180°﹣∠BEF=72°,
∵∠DBE=108°,
∴∠DBD'=∠DBE﹣∠D'BE=108°﹣72°=36°,
∵BD=6,
∴点D转动到点D′的路径长为=π(cm);
(2)过D作DG⊥BD'于G,过E作EH⊥BD'于H,如图:
Rt△BDG中,DG=BD sin36°≈6×0.59=3.54(cm),
Rt△BEH中,HE=BE sin72°≈4×0.95=3.80(cm),
∴DG+HE=3.54cm+3.80cm=7.34m≈7.3cm,
∵BD'∥EF,
∴点D到直线EF的距离约为7.3cm,
答:点D到直线EF的距离约为7.3cm.
15.解:(1)过点D作DH⊥CE于点H,
由题意知CD=2米,
∵斜坡CF的坡比为i=1:3,
∴,
设DH=x米,CH=3x米,
∵DH2+CH2=DC2,
∴,
∴x=2,
∴DH=2(米),CH=6(米),
答:王刚同学从点C到点D的过程中上升的高度为2米;
(2)过点D作DG⊥AB于点G,设BC=a米,
∵∠DHB=∠DGB=∠ABC=90°,
∴四边形DHBG为矩形,
∴DH=BG=2米,DG=BH=(a+6)米,
∵∠ACB=45°,
∴BC=AB=a(米),
∴AG=(a﹣2)米,
∵∠ADG=30°,
∴,
∴,
∴a=6+4,
∴AB=(6+4)(米).
答:大树AB的高度是(6+4)米.
16.解:延长BC交MN于点H,AD=BE=3.5,
设MH=x米,
∵∠MEC=45°,
∴EH=x米,
在Rt△MHB中,tan∠MBH==≈0.65,解得x=6.5,
则MN=1.6+6.5=8.1≈8(米),
∴电池板离地面的高度MN的长约为8米.
17.解:如图,
∵四边形AEFD为矩形,∠BAD=53°,
∴AD∥EF,∠E=∠F=90°,
∴∠BAD=∠EBA=53°,
在Rt△ABE中,∠E=90°,AB=10cm,∠EBA=53°,
∴sin∠EBA=≈0.80,cos∠EBA=≈0.60,
∴AE=8cm,BE=6cm,
∵∠ABC=90°,
∴∠FBC=90°﹣∠EBA=37°,
∴∠BCF=90°﹣∠FBC=53°,
在Rt△BCF中,∠F=90°,BC=6cm,
∴sin∠BCF=≈0.80,cos∠BCF=≈0.60,
∴BF=4.8cm,FC=3.6cm,
∴EF=6+4.8=10.8cm,
∴S四边形EFDA=AE EF=8×10.8=86.4(cm2),
S△ABE==×8×6=24(cm2),
S△BCF= BF CF=×4.8×3.6=8.64(cm2),
∴截面的面积=S四边形EFDA﹣S△ABE﹣S△BCF=86.4﹣24﹣8.64=53.76(cm2).
18.解:(1)过点B作BF⊥CH,垂足为F,延长AD交BF于E,垂足为E,则AE⊥BF,
由cos∠BAE=,
∴cos22°=,
∴,即AE=4.5m,
∴DE=AE﹣AD=4.5﹣0.4=4.1(m),
由sin∠BAE=,
∴,
∴,即BE=1.8m,
∴BF=BE+EF=1.8+1.2=3(m),
又,
∴,即CF=4m,
∴CH=CF+HF=CF+DE=4+4.1=8.1(m),即点O到岸边DH的距离为8.1m;
(2)过点B作BN⊥OH,垂足为N,延长AD交BN于点M,垂足为M,
由cos∠BAM=,
∴,
∴,
即AM=2.88m,
∴DM=AM﹣AD=2.88﹣0.4=2.48(m),
由sin∠BAM=,
∴,
∴,即BM=3.84m,
∴BN=BM+MN=3.84+1.2=5.04(m),
∴=(m),
∴OH=ON+HN=ON+DM=4.58(m),
即点O到岸边的距离为4.58m.
19.解:(1)设AD与BC交于点F,
由题意得BE∥AD,
∵BE∥AD且∠EBF=60°,
∴∠BFA=∠EBF=60°,
∵∠BFA=∠C+∠CAD且∠CAD=30°,
∴∠C=∠BFA﹣∠CAD=30°;
(2)过点B作BG⊥AD于G.
∵BG⊥AD,
∴∠AGB=∠BGD=90°,
在Rt△AGB中,AB=20米,∠BAG=45°,
AG=BG=20×sin45°=(米),
在Rt△BGF中,∠BFG=60°,
∴BF===(米),FG=BGtan60°===(米),
∵∠C=∠CAD=30°,
∴CF=AF=AG+FG=(10+)(米),
∴BC=BF+CF=(10+10)米,
答:两棵银杏树B、C之间的距离为(10+10)米.
20.解:由题意可知AB=24米,∠BDA=53°,
∴tan∠BDA==≈1.33,
∴AD=≈18.05(米).
∵tan∠CAD=tan30°===,
∴CD=18.05×≈10.4(米).
故办公楼的高度约为10.4米.
21.解:(1)如图,过点C作CE⊥AB于点E,
根据题意可知:∠ACE=∠CAE=45°,AC=25海里,
∴AE=CE=25(海里),
∵∠CBE=30°,
∴BE=25(海里),
∴BC=2CE=50(海里).
答:观测点B与C点之间的距离为50海里;
(2)如图,作CF⊥DB于点F,
∵CF⊥DB,FB⊥EB,CE⊥AB,
∴四边形CEBF是矩形,
∴FB=CE=25(海里),CF=BE=25(海里),
∴DF=BD+BF=30+25=55(海里),
在Rt△DCF中,根据勾股定理,得
CD===70(海里),
∴70÷42=(小时).
答:救援船到达C点需要的最少时间是小时.
