2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用题型分类训练(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用题型分类训练(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 12:33:38 | ||
图片预览

文档简介
2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》
题型分类训练(附答案)
一.解直角三角形
1.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么cos∠ACB值为( )
A. B. C. D.
2.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A. B. C. D.2
3.如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则sin∠DMN为( )
A. B. C. D.
4.如图,Rt△ABC中,∠ACB=90°,AB=5,AC=4,CD⊥AB于D,则tan∠BCD的值为( )
A. B. C. D.
5.如图,在Rt△ABC中,∠B=90°,∠ACB=45°,延长BC到D,使CD=AC,则tan22.5°=( )
A. B. C. D.
6.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于 .
7.如图,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB,交AC于E,若=,则tan∠A= .
8.已知AD是△ABC的高,CD=1,AD=BD=,则∠BAC= .
9.新定义:有一组对角互余的凸四边形称为对余四边形,如图,已知在对余四边形ABCD中,AB=10,BC=12,CD=5,tanB=,那么边AD的长为 .
10.△ABC中,∠ABC=30°,AB=4,AC=4,则BC= .
11.在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )
A.2 B. C. D.
12.如图,在△ABC中,∠ABC=90°,D为BC的中点,点E在AB上,AD,CE交于点F,AE=EF=4,FC=9,则cos∠ACB的值为( )
A. B. C. D.
13.如图,已知在△ABC中,∠ACB=90°,sinB=,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求的值.
14.如图,在10×6的正方形网格中,每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
(1)在图中以AB为边画Rt△ABC,点C在小正方形的格点上,使∠BAC=90°,且tan∠ACB=;
(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的格点上,使∠CBD=45°,连接CD,直接写出线段CD的长.
15.在Rt△ABC中,∠ACB=90°,点D是AC边上一点,连BD,过C点作BD的垂线与过A点作AC的垂线交于点E.当tan∠ABD=,cos∠E=,则的值是 .
二.解直角三角形的应用
16.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米 B.10米 C.10米 D.20米
17.某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
A.3.5sin29° B.3.5cos29° C.3.5tan29° D.
18.小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮筐底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知tanα=,则点D到地面的距离CD是( )
A.2.7米 B.3.0米 C.3.2米 D.3.4米
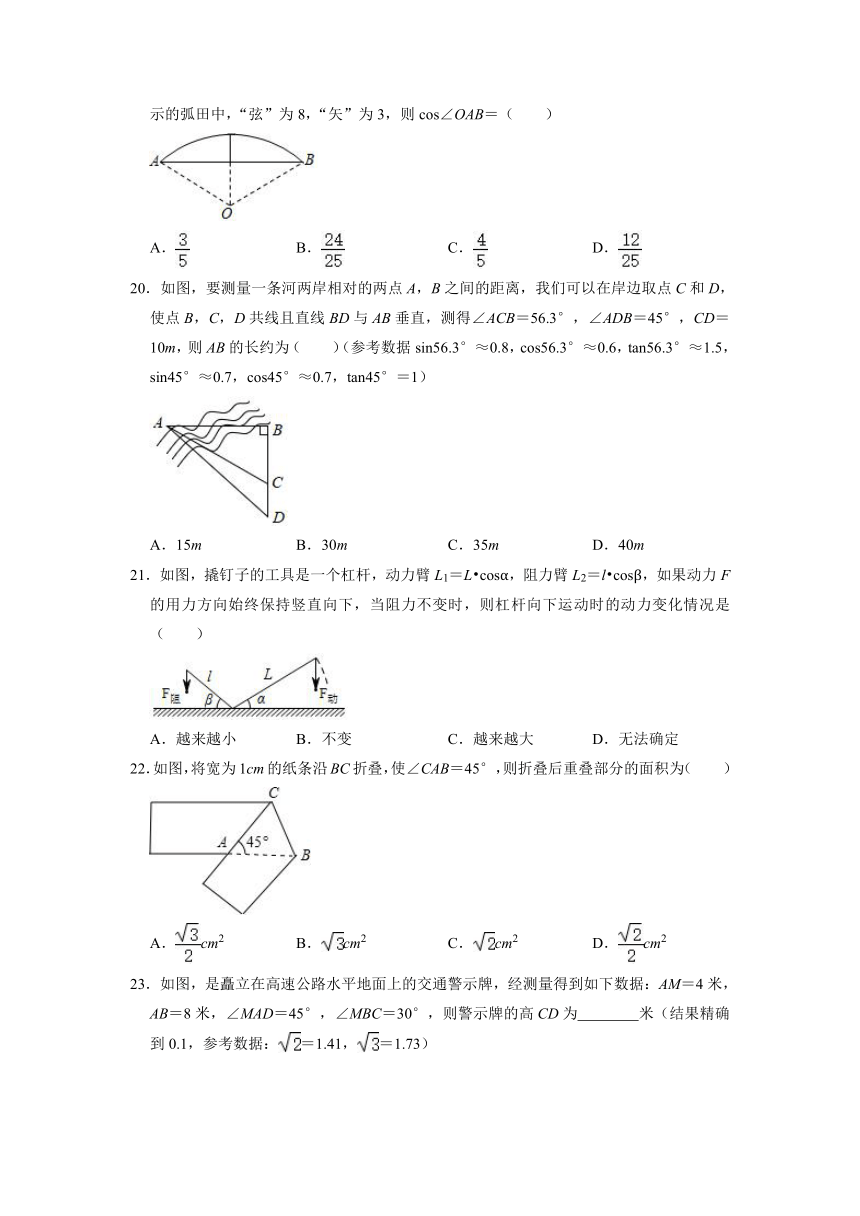
19.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积=(弦×矢+矢2),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长AB,“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为3,则cos∠OAB=( )
A. B. C. D.
20.如图,要测量一条河两岸相对的两点A,B之间的距离,我们可以在岸边取点C和D,使点B,C,D共线且直线BD与AB垂直,测得∠ACB=56.3°,∠ADB=45°,CD=10m,则AB的长约为( )(参考数据sin56.3°≈0.8,cos56.3°≈0.6,tan56.3°≈1.5,sin45°≈0.7,cos45°≈0.7,tan45°=1)
A.15m B.30m C.35m D.40m
21.如图,撬钉子的工具是一个杠杆,动力臂L1=L cosα,阻力臂L2=l cosβ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )
A.越来越小 B.不变 C.越来越大 D.无法确定
22.如图,将宽为1cm的纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为( )
A.cm2 B.cm2 C.cm2 D.cm2
23.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果精确到0.1,参考数据:=1.41,=1.73)
24.智能手机如果安装了一款测量软件“SmartMeasure”后,就可以测量物高、宽度和面积等,如图,打开软件后将手机摄像头对准脚部按键,再对准头部按键,即可测量出人体的高度.测量者AB用其数学原理如图②所示,测量一棵大树CD,手机显示AC=20m,AD=25m,∠CAD=53°,求此时CD的高.(结果保留根号)(sin53°≈,cos53°≈,tan53°≈)
25.如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.
(1)当吊臂底部A与货物的水平距离AC为5m时,求吊臂AB的长;
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计,计算结果精确到0.1m,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
26.如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=米,HF=米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:≈1.41,≈1.73)
27.如图,1号楼在2号楼的南侧,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=35m.请求出两楼之间的距离AB的长度(结果保留整数)
(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
28.如图,修公路遇到一座山,于是要修一条隧道,为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过点C作直线AB的垂线l,过点B作一直线(在山的旁边经过),与l相交于D点,经测量∠ABD=135°,BD=800m,求直线l上距离D点多远的C处开挖?(≈1.414,精确到1米)
29.图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②.其中AN表示平板电脑,M为AN上的定点,AN=CB=20cm,AM=8cm,MB=MN.我们把∠ANB叫做倾斜角.
(1)当倾斜角为45°时,求CN的长;
(2)按设计要求,倾斜角能小于30°吗?请说明理由.
三.解直角三角形的应用-坡度坡角问题
30.国家电网近来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD的平台BC上(如图),测得∠AED=52.5°,BC=5米,CD=35米,DE=19米,则铁塔AB的高度约为(参考数据:sin52.5°≈0.79,cos52.5°≈0.61,tan52.5°≈1.30)( )
A.7.6米 B.27.5米 C.30.5米 D.58.5米
31.如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为米,则斜坡AB的长度为( )
A. B. C. D.24
32.河堤横断面如图所示,斜坡AB的坡度=1:,AB=6m,则BC的长是( )
A.m B.3m C.m D.6m
33.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知sinα=,则小车上升的高度是( )
A.5米 B.6米 C.6.5米 D.7米
34.如图是拦水坝的横断面,堤高BC为6米,斜面坡度为1:2,则斜坡AB的长为( )
A.米 B.米 C.米 D.24米
35.某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角45°的传送带AB,调整为坡度i=1:的新传送带AC(如图所示).已知原传送带AB的长是4米,那么新传送带AC的长是( )
A.8米 B.4米 C.6米 D.3米
36.拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是 m.
37.如图是某货站传送货物的平面示意图为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角使其由45°改为30°,已知原传送带AB长为4米.
(1)求新传送带AC的长度;(结果保留根号)
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物DEFG是否需要挪走,并说明理由(结果精确到0.1米数据:≈1.41,≈1.73,≈2.45)
38.如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据:≈2.24,≈6.08,sin53°≈0.80,cos53°≈0.60)
四.解直角三角形的应用-仰角俯角问题
39.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )
A.2sinα B.2tanα C.2cosα D.
40.保利观澜旁边有一望江公园,公园里有一文峰塔,工程人员在与塔底中心的D同一水平线的A处,测得AD=20米,沿坡度i=0.75的斜坡AB走到B点,测得塔顶E仰角为37°,再沿水平方向走20米到C处,测得塔顶E的仰角为22°,则塔高DE为( )米.(结果精确到十分位)(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,)
A.18.3米 B.19.3米 C.20米 D.21.2米
41.如图,活动课小明利用一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为9m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )
A.3m B.27m C.(3+)m D.(27+)m
42.如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ高度为( )m.
A.6+2 B.6 C.10﹣ D.8
43.如图是自动扶梯的示意图.自动扶梯AB的倾斜角为30°在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A、C之间的距离为6m,则自动扶梯的垂直高度BD= m.(结果保留根号)
44.如图航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为60米,那么该建筑物高度BC约为 米.
45.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知乙楼的高CD是45m,则甲楼的高AB是 m(结果保留根号);
46.如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走2米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.则小明从点A走到点D的过程中,他上升的高度为 米;大树BC的高度为 米(结果保留根号)
47.某同学利用数学知识测量建筑物DEFG的高度.他从点A出发沿着坡度为i=1:2.4的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端D的仰角为37°,建筑物底端E的俯角为30°.若AF为水平的地面,测角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到0.1米,参考数据:≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)( )
A.23.0米 B.23.6米 C.26.7米 D.28.9米
五.解直角三角形的应用-方向角问题
48.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos55°海里
C.6sin55°海里 D.6tan55°海里
49.如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A.200tan70°米 B.米
C.200sin 70°米 D.米
50.如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我航海区域的C处截获可疑渔船,问我渔政船的航行路程是 海里(结果保留根号).
51.如图,某渔船在完成捕捞作业后准备返回港口C,途经某海域A处时,港口C的工作人员监测到点A在南偏东30°方向上,另一港口B的工作人员监测到点A在正西方向上.已知港口C在港口B的北偏西60°方向,且B、C两地相距120海里.
(1)求出此时点A到港口C的距离(计算结果保留根号);
(2)若该渔船从A处沿AC方向向港口C驶去,当到达点A'时,测得港口B在A'的南偏东75°的方向上,求此时渔船的航行距离(计算结果保留根号).
52.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,
(1)求B到C的距离;
(2)如果在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由(≈1.732).
53.一艘轮船由南向北航行,如图,在A处测得小岛P在北偏西15°方向上,两个小时后,轮船在B处测得小岛P在北偏西30°方向上,在小岛周围18海里内有暗礁,问若轮船按20海里/时的速度继续向北航行,有无触礁的危险?
54.如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.≈1.414,≈1.732).
55.如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛40nmile的点A处,它沿着点A的南偏东15°的方向航行.
(1)渔船航行多远距离小岛B最近(结果保留根号)?
(2)渔船到达距离小岛B最近点后,按原航向继续航行20nmile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?
56.如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台风中心距离小岛200海里.
(1)过点B作BP⊥AC于点P,求∠PBC的度数;
(2)据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响?请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60,≈1.73)
参考答案
一.解直角三角形
1.解:如图,过点A作AH⊥BC于H.
在Rt△ACH中,∵AH=4,CH=3,
∴AC===5,
∴cos∠ACB==,
故选:C.
2.解:延长AD、BC,两线交于O,
∵在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:C.
3.解:连接AD,如图,
∵∠A=90°,AB=6,AC=8,
∴BC=10,
∵点D为边BC的中点,
∴DA=DC=5,
∴∠1=∠C,
∵∠MDN=90°,∠A=90°,
∴点A、D在以MN为直径的圆上,
∴∠1=∠DMN,
∴∠C=∠DMN,
在Rt△ABC中,sinC===,
∴sin∠DMN=,
故选:A.
4.解:∵∠ACB=90°,AB=5,AC=4,
∴BC=3,
在Rt△ABC与Rt△BCD中,∠A+∠B=90°,∠BCD+∠B=90°.
∴∠A=∠BCD.
∴tan∠BCD=tanA==,
故选:D.
5.解:设AB=x,
∵在Rt△ABC中,∠B=90°,∠ACB=45°,
∴∠BAC=∠ACB=45°,
∴AB=BC=x,
由勾股定理得:AC==x,
∵AC=CD,
∴AC=CD=x,
∴BD=BC+CD=(+1)x,
∴tan22.5°===﹣1,
故选:B.
6.解:作CD⊥AB于点D,作AE⊥BC于点E,
由已知可得,AC==,AB=5,BC==5,CD=3,
∵,
∴,
解得AE=3,
∴CE===1,
∴cos∠ACB===,
故答案为:.
7.解:连接EB,
∵D是AB的中点,DE⊥AB,
∴DE是AB的垂直平分线,
∴EA=EB,
∵==,
设EC=3k,则AE=BE=5k,AC=5k+3k=8k,
在Rt△BCE中,BC==4k,
在Rt△ABC中,tan∠A===,
故答案为:.
8.解:如图所示:
①tan∠BAD==1,∴∠BAD=45°,
tan∠CAD==,∴∠CAD=30°,
∴∠BAC=45°+30°=75°;
②tan∠BAD==1,∴∠BAD=45°,
tan∠CAD==,∴∠CAD=30°,
∴∠BAC=45°﹣30°=15°.
故∠BAC=75°或15°.
9.解:如图,过端午A作AH⊥BC于H,过点C作CE⊥AD于E,连接AC.
在Rt△ABH中,tanB==,
∴可以假设AH=3k,BH=4k,则AB=5k=10,
∴k=2,
∴AH=6,BH=8,
∵BC=12,
∴CH=BC﹣BH=12﹣8=4,
∴AC===2,
∵∠B+∠D=90°,∠D+∠ECD=90°,
∴∠ECD=∠B,
在Rt△CED中,tan∠ECD==,
∵CD=5,
∴DE=3,CE=4,
∴AE===6,
∴AD=AE+DE=9.
故答案为:9.
10.解:①当∠ACB为锐角时,如图1,过点A作AD⊥BC,垂足为D,
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD+DC=6+2=8;
②当∠ACB为钝角时,如图2,过点A作AD⊥BC,交BC的延长线于点D,
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD﹣DC=6﹣2=4;
因此BC的长为8或4,
故答案为:8或4.
11.解:如图,取格点K,连接AK,BK.
观察图形可知AK⊥BK,BK=2AK,BK∥CD,
∴∠AED=∠ABK,
∴tan∠AED=tan∠ABK==,
故选:B.
12.解:如图,延长AD到M,使得DM=DF,连接BM.
∵BD=DC,∠BDM=∠CDF,DM=DF,
∴△BDM≌△CDF(SAS),
∴CF=BM=9,∠M=∠CFD,
∵CE∥BM,
∴∠AFE=∠M,
∵EA=EF,
∴∠EAF=∠EFA,
∴∠BAM=∠M,
∴AB=BM=9,
∵AE=4,
∴BE=5,
∵∠EBC=90°,
∴BC===12,
∴AC===15,
∴cos∠ACB===,
解法二:过点D作DG平行AC,构造三角形BDG相似于三角形BCG,同理AEF相似于AGD,再由题目条件,可得cos角ACB的值,遇到分点问题想平行,构造A或8字型相似.
故选:D.
13.解:(1)过点C作CG⊥AB,垂足为G,
∵∠ACB=90°,
∴∠ACG=∠B,
在△ABC中,sinB=,设AC=3x,则AB=5x,BC=4x,
∴sin∠ACG===sinB,
∴AG=x,CG=x,
∴DG=DA+AG=3x+x=x,
在Rt△DCG中,tan∠D==;
(2)过点C作CH∥DB,交BF的延长线于点H,则有△CHF∽△DBF,
又有E是AC的中点,可证△CHE≌△ABE,
∴HC=AB=5x,
由△CHF∽△DBF得:===.
14.解:(1)如图,
由勾股定理得:AB==2,
AC==3,BC==,
∴AB2+AC2=(2)2+(3)2=26,
BC2=()2=26,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
tan∠ACB===;
(2)如图,∵S△DEF=×2×3=3,
∵BC=,CD==,BD==,
∴BC2+CD2=52,BD2=52,
∴BC2+CD2=BD2,
∴∠BCD=90°,BC=CD,
∴∠CBD=45°,
∴CD=.
15.解:设直线AB交CE于点H,BD交CE于点N,
设∠E=α,则cos∠E==cosα,则sinα=,tanα=4,
∵tan∠ABD=,则tan∠BHN=2,
∵AE⊥AC,BC⊥AC,
∴AE∥BC,
∴∠E=∠ECB=α,
∵∠NDC+∠NCD=90°,∠NCB+∠NCD=90°,
∴∠NCB=∠NDC=α,
在△AHE中,设AE=a,则AG=AEsinα=asinα,GE=acosα,
则GH===AG=asinα,则EH=GE+GH=acosα+asinα,
在Rt△AEC中,EC==,
则HC=EC﹣EH=﹣(acosα+asinα);
在△BHC中,tan∠BHN=2,tanα=4,HC=﹣(acosα+asinα),
同理可得:BC=×,
在Rt△BCD中,CD==×=a(﹣﹣)=,
AD=AC﹣CD=4a﹣=,
则=,故答案为.
二.解直角三角形的应用
16.解:∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=60°,
∴∠ABD=60°﹣30°=30°,
∴∠A=∠ABD,
∴BD=AD=20米,
∴BC=BD sin60°=10(米),故选:C.
17.解:在Rt△ABC中,∵∠A=90°,BC=3.5米,∠BCA=29°,
∴AB=BC sin∠ACB=3.5 sin29°,
故选:A.
18.解:在直角△ADE中,∠DAE=α,AE=5米,tan,
∴tanα===,
∴DE=1.5米.
又CE=AB=1.7米,
∴CD=CE+DE=3.2米.故选:C.
19.解:如图,作OH⊥AB于H.
由题意:AB=8,OA﹣OH=3,
∵OH⊥AB,
∴AH=BH=4,
∵AH2+OH2=OA2,
∴42=(OA+OH)(OA﹣OH),
∴OA+OH=,
∴OA=,OH=,
∴cos∠OAB===,
故选:B.
20.解:设AB=xm,
在Rt△ABD中,∵∠ADB=45°,
∴AB=BD=xm,
在Rt△ABC中,∵∠ACB=56.3°,且tan∠ACB=,
∴BC==≈x,
由BC+CD=BD得x+10=x,
解得x=30,
∴AB的长约为30m,
故选:B.
21.解:∵动力×动力臂=阻力×阻力臂,
∴当阻力及阻力臂不变时,动力×动力臂为定值,且定值>0,
∴动力随着动力臂的增大而减小,
∵杠杆向下运动时α的度数越来越小,此时cosα的值越来越大,而β的度数越来越大,cosβ的值越来越小,
∴阻力臂越来越小,而阻力不变,
∴动力×动力臂越来越小,而动力臂越来越大,
∴此时的动力越来越小,
故选:A.
22.解:如图,∵CE∥AB,
∴∠ECB=∠ABC,
∵∠ECB=∠ACB,
∴∠ACB=∠ABC,
∴AC=AB,
作CD⊥AB,垂足为D,
则CD=1.
∵sin∠A=,
∴==AB,
∴S△ABC=×AB×CD=,
∴折叠后重叠部分的面积为cm2.
故选:D.
23.解:由题意可得:∵AM=4米,∠MAD=45°,
∴DM=4m,
∵AM=4米,AB=8米,
∴MB=12米,
∵∠MBC=30°,
∴BC=2MC,
∴MC2+MB2=(2MC)2,
MC2+122=(2MC)2,
∴MC=4,
则DC=4﹣4≈2.9(米),
故答案为:2.9.
24.解:如图②中,过点D作DH⊥AC于H,
在Rt△ADH中,cos∠CAD=,sin∠CAD=,
∴AH=AD cos53°≈25×=15(m),DH=AD sin53°≈25×=20(m),
∵AC=20m,
∴CH=AC﹣AH=5(m),
∴CD===5(m).
25.解:(1)在Rt△ABC中,
∵∠BAC=64°,AC=5m,
∴AB=≈5÷0.44≈11.4(m);
故答案为:11.4;
(2)过点D作DH⊥地面于H,交水平线于点E,
在Rt△ADE中,
∵AD=20m,∠DAE=64°,EH=1.5m,
∴DE=sin64°×AD≈20×0.9≈18(m),
即DH=DE+EH=18+1.5=19.5(m),
答:如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是19.5m.
26.解:(1)在Rt△EFH中,cos∠FHE===,
∴∠FHE=45°.
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan60°=1.3×=1.3(米),
∴GM=AB=1.3(米),
在Rt△ANH中,∠FAN=∠FHE=45°,
∴HN=AHsin45°=×=(米),
∴EM=EG+GM=+1.3≈2.75(米).
答:篮板底部点E到地面的距离大约是2.75米.
27.解:过点C作CE⊥PB,垂足为E,过点D作DF⊥PB,垂足为F,
则∠CEP=∠PFD=90°,
由题意可知:设AB=x,
在Rt△PCE中,tan32.3°=,
∴PE=x tan32.3°,
同理可得:在Rt△PDF中,tan55.7°=,
∴PF=x tan55.7°,
由PF﹣PE=EF=CD=35,
可得x tan55.7°﹣x tan32.3°=35,
解得:x=42.
∴楼间距AB的长度约为42m.
28.解:∵CD⊥AC,
∴∠ACD=90°,
∵∠ABD=135°,
∴∠DBC=45°,
∴∠D=45°,
∴CB=CD,
在Rt△DCB中:CD2+BC2=BD2,
2CD2=8002,
CD=400≈566(米),
答:直线L上距离D点566米的C处开挖.
29.解:(1)当∠ANB=45°时,
∵MB=MN,
∴∠B=∠ANB=45°,
∴∠NMB=180°﹣∠ANB﹣∠B=90°.
在Rt△NMB中,sin∠B=,
∴BN===12cm.
∴CN=CB﹣BN=AN﹣BN=(20﹣12)cm.
(2)当∠ANB=30°时,作ME⊥CB,垂足为E.
∵MB=MN,
∴∠B=∠ANB=30°
在Rt△BEM中,cos∠B=,
∴BE=MB cos∠B=(AN﹣AM) cos∠B=6cm.
∵MB=MN,ME⊥CB,
∴BN=2BE=12cm.
∵CB=AN=20cm,且12>20,
∴此时N不在CB边上,与题目条件不符.
随着∠ANB度数的减小,BN长度在增加,
∴倾斜角不可以小于30°.
三.解直角三角形的应用-坡度坡角问题
30.解:延长AB交ED于G,过C作CF⊥DE于F,
∴GF=BC=5(米),
∵山坡CD的坡度为1:0.75,
∴设DF=3k,CF=4k,
∴CD=5k=35(米),
∴k=7(米),
∴DF=21米,BG=CF=28米,
∴EG=GF+DF+DE=5+21+19=45(米),
∵∠AED=52°,
∴AG=EG tan52.5°≈45×1.30=58.5(米),
∴AB=30.5米,
答:铁塔AB的高度约为30.5米.
故选:C.
31.解:过B作BE⊥AD于E,过C作CF⊥AD于F,如图所示:
则四边形BEFC是矩形,
∴BE=CF,
∵背水坡CD的坡比i=1:1,CD=米,
∴CF=DF=CD=6(米),
∴BE=CF=6米,
又∵斜坡AB的坡比i=1:2=,
∴AE=2BE=12(米),
∴AB===6(米),
故选:C.
32.解:Rt△ABC中,tan∠BAC=斜坡AB的坡度=1:=,
∴∠BAC=30°,
∵BC⊥AC,
∴BC=AB=3m,
故选:B.
33.解:如图AC=13,作CB⊥AB,
∵sinα==,
∴BC=5,
∴小车上升的高度是5m.
故选:A.
34.解:∵斜面坡度为1:2,BC=6m,
∴AC=12m,
则AB=(m).
故选:B.
35.解:过点A作AD⊥CB延长线于点D,
∵∠ABD=45°,
∴AD=BD,
∵AB=4,
∴AD=BD=ABsin45°=4×=4,
∵坡度i=1:,
∴,
则DC=4,
故AC==8(m).
故选:A.
36.解:∵迎水坡AB的坡比是1:,坝高BC=10m,
∴==,
解得:AC=10,
则AB==20(m).
故答案为:20.
37.解:(1)如图,
在Rt△ABM中,AM=ABsin45°=2(米).
在Rt△ACM中,
∵∠ACM=30°,
∴AC=2AM=4(米).
即新传送带AC的长度约为4米;
(2)结论:货物DEFG不用挪走.
解:在Rt△ABM中,BM=ABcos45°=2(米).
在Rt△ACM中,CM=AM=2(米).
∴CB=CM﹣BM=2﹣2≈2.08(米).
∵DC=DB﹣CB≈5﹣2.08=2.92(米)>2(米),
∴货物DEFG不应挪走.
38.解:(1)由题意CD=CH,
在Rt△ACH中,CH==2≈12.2(cm).
∴CD=CH=12.2(cm).
(2)如图2中,过点E作EK⊥PC于K.
在Rt△ECK中,EK=EC sin53°≈4(cm),CK=EC cos53°≈3(cm),
在Rt△EPK中,PK===2≈4.48(cm),
∴DP=CD﹣CK﹣PK﹣MN=12.2﹣3﹣4.48﹣2=2.72>2.5,
∴能在ND处装入一段长为2.5cm的订书钉.
四.解直角三角形的应用-仰角俯角问题
39.解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC tanα=2tanα,
故选:B.
40.解:连接DE,作BF⊥DE于F,BG⊥DA于G,如图:
则DF=BG,BF=DG=AD+AG,
∵AB=斜坡AB的坡度i=0.75=,
∴设BG=3xm,则AG=4xm,BF=DG=20+4x(m),CF=BF+BC=20+4x+20=40+4x(m),
由题意得:∠EBF=37°,∠ECF=22°,
∵tan∠BEF==,tan∠ECF==,
∴EF=tan37°(20+4x),EF=tan22°(40+4x),
∴0.75(20+4x)=0.40(40+4x),
解得:x=,
∴DF=BG=3x=(m),
EF=0.40(40+4x)=(m),
∴DE=DF+EF=+≈19.3(m);
故选:B.
41.解:∵AB⊥BE,DE⊥BE,AD∥BE,
∴四边形ABED是矩形,
∵BE=9m,AB=1.5m,
∴AD=BE=9m,DE=AB=1.5m,
在Rt△ACD中,
∵∠CAD=30°,AD=9m,
∴CD=AD tan30°=9×=3,
∴CE=CD+DE=3+1.5
故选:C.
42.解:延长PQ交直线AB于点E,设PE=x米.
在直角△APE中,∠A=45°,
则AE=PE=x米;
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中,BE=PE=x米,
∵AB=AE﹣BE=6米,
则x﹣x=6,
解得:x=9+3.
则BE=(3+3)米.
在直角△BEQ中,QE=BE=(3+3)=(3+)米.
∴PQ=PE﹣QE=9+3﹣(3+)=6+2(米).
答:电线杆PQ的高度是6+2(米).
故选:A.
43.解:∵∠BCD=∠BAC+∠ABC,∠BAC=30°,∠BCD=60°,
∴∠ABC=∠BCD﹣∠BAC=30°,
∴∠BAC=∠ABC,
∴BC=AC=6m,
在Rt△BDC中,
∵BD=BC sin∠BCD=6×=3(m),
故答案为:3.
44.解:由题意可得:tan30°===,
解得:BD=20(米),
tan60°===,
解得:DC=60(米),
故该建筑物的高度为:BC=BD+DC=80(米)
故答案为80.
45.解:由题意可得:∠BDA=45°,
则AB=AD,
又∵∠CAD=30°,
∴在Rt△ADC中,CD=45m.
tan∠CDA=tan30°==,即=,
解得:AD=45(m),
∴AB=45m.
故答案为:45.
46.解:如图,过点D作DK⊥BC于K,DH⊥CE于H,
则四边形DHCK为矩形.
故DK=CH,CK=DH,
在直角三角形AHD中,=,AD=2米,
∴DH=2米,AH=4米,
∴CK=DH=2米,
设BC=x米,
在直角三角形ABC中,AC==x米,
∴DK=(4+x)米,BK=(x﹣2)米,
在直角三角形BDK中,∵BK=DK tan30°,
∴x﹣2=(4+x)×,
解得:x=5+3,
∴BC=(5+3 )米.
答:大树的高度为(3+5)米.
故答案是:2;(3+5).
47.解:如图所示:过点B作BN⊥AE,CM⊥DE垂足分别为:N,M,
∵i=1:2.4,AB=26m,
∴设BN=x,则AN=2.4x,
∴AB=2.6x,
则2.6x=26,
解得:x=10,
故BN=10,
∴CN=ME=11.6,
则tan30°===,
解得:CM=11.6,
则tan37°===0.75,
解得:DM≈15.1(m),
故DE=DM+EM=15.1+11.6=26.7(m).
故选:C.
五.解直角三角形的应用-方向角问题
48.解:如图所示:
由题意可知∠NPA=55°,PA=6海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=55°.
在Rt△ABP中,∵∠ABP=90°,∠A=55°,PA=6海里,
∴AB=AP cos∠A=6cos55°海里.
故选:B.
49.解:在Rt△PQT中,
∵∠QPT=90°,∠PQT=90°﹣70°=20°,
∴∠PTQ=70°,
∴tan70°=,
∴PT==,
即河宽米,
故选:B.
50.解:作CD⊥AB于点D,垂足为D,
在Rt△BCD中,
∵BC=12×1.5=18(海里),∠CBD=45°,
∴CD=BC sin45°=18×=9(海里),
则在Rt△ACD中,
AC==9×2=18(海里).
故我渔政船航行了18海里.
故答案为:18.
51.解:(1)如图所示:延长BA,过点C作CD⊥BA延长线于点D,
由题意可得:∠CBD=30°,BC=120海里,
则CD=BC=60海里,
∵cos∠ACD==cos30°=,
即=,
∴AC=40(海里),
答:此时点A到军港C的距离为40海里;
(2)过点A′作A′N⊥BC于点N,如图:
由(1)得:CD=60海里,AC=40海里,
∵A'E∥CD,
∴∠AA'E=∠ACD=30°,
∴∠BA′A=45°,
∵∠BA'E=75°,
∴∠ABA'=15°,
∴∠2=15°=∠ABA',
即A′B平分∠CBA,
∴A'E=A'N,
设AA′=x,则AE=AA',A'N=A′E=AE=x,
∵∠1=60°﹣30°=30°,A'N⊥BC,
∴A'C=2A'N=x,
∵A'C+AA'=AC,
∴x+x=40,
解得:x=60﹣20,
∴AA'=(60﹣20)海里,
答:此时渔船的航行距离为(60﹣20)海里.
52.解:(1)由题意得:∠BAC=90°﹣60°=30°,∠MBC=90°﹣30°=60°,
∵∠MBC=∠BAC+∠ACB,
∴∠ACB=∠MBC﹣∠BAC=30°,
∴∠BAC=∠ACB,
∴BC=AB=24×=12(海里);
(2)该货船无触礁危险,理由如下:
过点C作CD⊥AD于点D,如图所示:
∵∠EAC=60°,∠FBC=30°,
∴∠CAB=30°,∠CBD=60°.
∴在Rt△CBD中,CD=BD.
在Rt△CAD中,AD=CD=3BD=AB+BD=12+BD,
∴BD=6.
∴CD=6.
∵6>9,
∴货船继续向正东方向行驶无触礁危险.
53.解:如图,作PD⊥AB交AB延长线于D点,
∵∠PBC=30°,
∴∠PAB=15°,
∴∠APB=∠PBC﹣∠PAB=15°,
∴PB=AB=20×2=40 (海里),
在Rt△BPD中,
∴PD=PB=20(海里),
∵20>18,
∴不会触礁.
54.解:过P作PC⊥AB于点C,
∴∠ACP=90°.
由题意可知,∠PAC=30°,∠PBC=45°.
∴∠BPC=45°.
∴BC=PC.
在Rt△ACP中,.
∵AB=20,
∴.
∴≈27.3.
答:河流宽度约为27.3米.
55.解:(1)过B作BM⊥AC于M,
由题意可知∠BAM=45°,则∠ABM=45°,
在Rt△ABM中,∵∠BAM=45°,AB=40nmile,
∴BM=AM=AB=20nmile,
∴渔船航行20nmile距离小岛B最近;
(2)∵BM=20nmile,MC=20nmile,
∴tan∠MBC===,
∴∠MBC=60°,
∴∠CBG=180°﹣60°﹣45°﹣30°=45°,
在Rt△BCM中,∵∠CBM=60°,BM=20nmile,
∴BC==2BM=40nmile,
故救援队从B处出发沿点B的南偏东45°的方向航行到达事故地点航程最短,最短航程是40nmile.
56.解:(1)∵∠MAC=60°,
∴∠BAC=30°,
又∵BP⊥AC,
∴∠APB=90°,
∴∠ABP=60°,
又∵∠CBN=29°,∠ABN=90°,
∴∠ABC=119°,
∴∠PBC=∠ABC﹣∠ABP=59°;
(2)不会受到影响.理由如下:
由(1)可知,∠PBC=59°,
∴∠C=90°﹣∠PBC=31°,
又∵tan31°=0.60,
∴,
设BP为x海里,
则AP=海里,CP=海里,
∴,
解得:x≈59,
∵59>50,
∴沿海城市B不会受到台风影响.
题型分类训练(附答案)
一.解直角三角形
1.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么cos∠ACB值为( )
A. B. C. D.
2.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A. B. C. D.2
3.如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则sin∠DMN为( )
A. B. C. D.
4.如图,Rt△ABC中,∠ACB=90°,AB=5,AC=4,CD⊥AB于D,则tan∠BCD的值为( )
A. B. C. D.
5.如图,在Rt△ABC中,∠B=90°,∠ACB=45°,延长BC到D,使CD=AC,则tan22.5°=( )
A. B. C. D.
6.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于 .
7.如图,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB,交AC于E,若=,则tan∠A= .
8.已知AD是△ABC的高,CD=1,AD=BD=,则∠BAC= .
9.新定义:有一组对角互余的凸四边形称为对余四边形,如图,已知在对余四边形ABCD中,AB=10,BC=12,CD=5,tanB=,那么边AD的长为 .
10.△ABC中,∠ABC=30°,AB=4,AC=4,则BC= .
11.在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )
A.2 B. C. D.
12.如图,在△ABC中,∠ABC=90°,D为BC的中点,点E在AB上,AD,CE交于点F,AE=EF=4,FC=9,则cos∠ACB的值为( )
A. B. C. D.
13.如图,已知在△ABC中,∠ACB=90°,sinB=,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求的值.
14.如图,在10×6的正方形网格中,每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
(1)在图中以AB为边画Rt△ABC,点C在小正方形的格点上,使∠BAC=90°,且tan∠ACB=;
(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的格点上,使∠CBD=45°,连接CD,直接写出线段CD的长.
15.在Rt△ABC中,∠ACB=90°,点D是AC边上一点,连BD,过C点作BD的垂线与过A点作AC的垂线交于点E.当tan∠ABD=,cos∠E=,则的值是 .
二.解直角三角形的应用
16.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米 B.10米 C.10米 D.20米
17.某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
A.3.5sin29° B.3.5cos29° C.3.5tan29° D.
18.小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮筐底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知tanα=,则点D到地面的距离CD是( )
A.2.7米 B.3.0米 C.3.2米 D.3.4米
19.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积=(弦×矢+矢2),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长AB,“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为3,则cos∠OAB=( )
A. B. C. D.
20.如图,要测量一条河两岸相对的两点A,B之间的距离,我们可以在岸边取点C和D,使点B,C,D共线且直线BD与AB垂直,测得∠ACB=56.3°,∠ADB=45°,CD=10m,则AB的长约为( )(参考数据sin56.3°≈0.8,cos56.3°≈0.6,tan56.3°≈1.5,sin45°≈0.7,cos45°≈0.7,tan45°=1)
A.15m B.30m C.35m D.40m
21.如图,撬钉子的工具是一个杠杆,动力臂L1=L cosα,阻力臂L2=l cosβ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )
A.越来越小 B.不变 C.越来越大 D.无法确定
22.如图,将宽为1cm的纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为( )
A.cm2 B.cm2 C.cm2 D.cm2
23.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果精确到0.1,参考数据:=1.41,=1.73)
24.智能手机如果安装了一款测量软件“SmartMeasure”后,就可以测量物高、宽度和面积等,如图,打开软件后将手机摄像头对准脚部按键,再对准头部按键,即可测量出人体的高度.测量者AB用其数学原理如图②所示,测量一棵大树CD,手机显示AC=20m,AD=25m,∠CAD=53°,求此时CD的高.(结果保留根号)(sin53°≈,cos53°≈,tan53°≈)
25.如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.
(1)当吊臂底部A与货物的水平距离AC为5m时,求吊臂AB的长;
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计,计算结果精确到0.1m,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
26.如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=米,HF=米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:≈1.41,≈1.73)
27.如图,1号楼在2号楼的南侧,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=35m.请求出两楼之间的距离AB的长度(结果保留整数)
(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
28.如图,修公路遇到一座山,于是要修一条隧道,为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过点C作直线AB的垂线l,过点B作一直线(在山的旁边经过),与l相交于D点,经测量∠ABD=135°,BD=800m,求直线l上距离D点多远的C处开挖?(≈1.414,精确到1米)
29.图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②.其中AN表示平板电脑,M为AN上的定点,AN=CB=20cm,AM=8cm,MB=MN.我们把∠ANB叫做倾斜角.
(1)当倾斜角为45°时,求CN的长;
(2)按设计要求,倾斜角能小于30°吗?请说明理由.
三.解直角三角形的应用-坡度坡角问题
30.国家电网近来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD的平台BC上(如图),测得∠AED=52.5°,BC=5米,CD=35米,DE=19米,则铁塔AB的高度约为(参考数据:sin52.5°≈0.79,cos52.5°≈0.61,tan52.5°≈1.30)( )
A.7.6米 B.27.5米 C.30.5米 D.58.5米
31.如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为米,则斜坡AB的长度为( )
A. B. C. D.24
32.河堤横断面如图所示,斜坡AB的坡度=1:,AB=6m,则BC的长是( )
A.m B.3m C.m D.6m
33.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知sinα=,则小车上升的高度是( )
A.5米 B.6米 C.6.5米 D.7米
34.如图是拦水坝的横断面,堤高BC为6米,斜面坡度为1:2,则斜坡AB的长为( )
A.米 B.米 C.米 D.24米
35.某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角45°的传送带AB,调整为坡度i=1:的新传送带AC(如图所示).已知原传送带AB的长是4米,那么新传送带AC的长是( )
A.8米 B.4米 C.6米 D.3米
36.拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是 m.
37.如图是某货站传送货物的平面示意图为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角使其由45°改为30°,已知原传送带AB长为4米.
(1)求新传送带AC的长度;(结果保留根号)
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物DEFG是否需要挪走,并说明理由(结果精确到0.1米数据:≈1.41,≈1.73,≈2.45)
38.如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据:≈2.24,≈6.08,sin53°≈0.80,cos53°≈0.60)
四.解直角三角形的应用-仰角俯角问题
39.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )
A.2sinα B.2tanα C.2cosα D.
40.保利观澜旁边有一望江公园,公园里有一文峰塔,工程人员在与塔底中心的D同一水平线的A处,测得AD=20米,沿坡度i=0.75的斜坡AB走到B点,测得塔顶E仰角为37°,再沿水平方向走20米到C处,测得塔顶E的仰角为22°,则塔高DE为( )米.(结果精确到十分位)(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,)
A.18.3米 B.19.3米 C.20米 D.21.2米
41.如图,活动课小明利用一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为9m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )
A.3m B.27m C.(3+)m D.(27+)m
42.如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ高度为( )m.
A.6+2 B.6 C.10﹣ D.8
43.如图是自动扶梯的示意图.自动扶梯AB的倾斜角为30°在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A、C之间的距离为6m,则自动扶梯的垂直高度BD= m.(结果保留根号)
44.如图航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为60米,那么该建筑物高度BC约为 米.
45.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知乙楼的高CD是45m,则甲楼的高AB是 m(结果保留根号);
46.如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走2米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.则小明从点A走到点D的过程中,他上升的高度为 米;大树BC的高度为 米(结果保留根号)
47.某同学利用数学知识测量建筑物DEFG的高度.他从点A出发沿着坡度为i=1:2.4的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端D的仰角为37°,建筑物底端E的俯角为30°.若AF为水平的地面,测角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到0.1米,参考数据:≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)( )
A.23.0米 B.23.6米 C.26.7米 D.28.9米
五.解直角三角形的应用-方向角问题
48.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos55°海里
C.6sin55°海里 D.6tan55°海里
49.如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A.200tan70°米 B.米
C.200sin 70°米 D.米
50.如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我航海区域的C处截获可疑渔船,问我渔政船的航行路程是 海里(结果保留根号).
51.如图,某渔船在完成捕捞作业后准备返回港口C,途经某海域A处时,港口C的工作人员监测到点A在南偏东30°方向上,另一港口B的工作人员监测到点A在正西方向上.已知港口C在港口B的北偏西60°方向,且B、C两地相距120海里.
(1)求出此时点A到港口C的距离(计算结果保留根号);
(2)若该渔船从A处沿AC方向向港口C驶去,当到达点A'时,测得港口B在A'的南偏东75°的方向上,求此时渔船的航行距离(计算结果保留根号).
52.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,
(1)求B到C的距离;
(2)如果在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由(≈1.732).
53.一艘轮船由南向北航行,如图,在A处测得小岛P在北偏西15°方向上,两个小时后,轮船在B处测得小岛P在北偏西30°方向上,在小岛周围18海里内有暗礁,问若轮船按20海里/时的速度继续向北航行,有无触礁的危险?
54.如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.≈1.414,≈1.732).
55.如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛40nmile的点A处,它沿着点A的南偏东15°的方向航行.
(1)渔船航行多远距离小岛B最近(结果保留根号)?
(2)渔船到达距离小岛B最近点后,按原航向继续航行20nmile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?
56.如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台风中心距离小岛200海里.
(1)过点B作BP⊥AC于点P,求∠PBC的度数;
(2)据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响?请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60,≈1.73)
参考答案
一.解直角三角形
1.解:如图,过点A作AH⊥BC于H.
在Rt△ACH中,∵AH=4,CH=3,
∴AC===5,
∴cos∠ACB==,
故选:C.
2.解:延长AD、BC,两线交于O,
∵在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:C.
3.解:连接AD,如图,
∵∠A=90°,AB=6,AC=8,
∴BC=10,
∵点D为边BC的中点,
∴DA=DC=5,
∴∠1=∠C,
∵∠MDN=90°,∠A=90°,
∴点A、D在以MN为直径的圆上,
∴∠1=∠DMN,
∴∠C=∠DMN,
在Rt△ABC中,sinC===,
∴sin∠DMN=,
故选:A.
4.解:∵∠ACB=90°,AB=5,AC=4,
∴BC=3,
在Rt△ABC与Rt△BCD中,∠A+∠B=90°,∠BCD+∠B=90°.
∴∠A=∠BCD.
∴tan∠BCD=tanA==,
故选:D.
5.解:设AB=x,
∵在Rt△ABC中,∠B=90°,∠ACB=45°,
∴∠BAC=∠ACB=45°,
∴AB=BC=x,
由勾股定理得:AC==x,
∵AC=CD,
∴AC=CD=x,
∴BD=BC+CD=(+1)x,
∴tan22.5°===﹣1,
故选:B.
6.解:作CD⊥AB于点D,作AE⊥BC于点E,
由已知可得,AC==,AB=5,BC==5,CD=3,
∵,
∴,
解得AE=3,
∴CE===1,
∴cos∠ACB===,
故答案为:.
7.解:连接EB,
∵D是AB的中点,DE⊥AB,
∴DE是AB的垂直平分线,
∴EA=EB,
∵==,
设EC=3k,则AE=BE=5k,AC=5k+3k=8k,
在Rt△BCE中,BC==4k,
在Rt△ABC中,tan∠A===,
故答案为:.
8.解:如图所示:
①tan∠BAD==1,∴∠BAD=45°,
tan∠CAD==,∴∠CAD=30°,
∴∠BAC=45°+30°=75°;
②tan∠BAD==1,∴∠BAD=45°,
tan∠CAD==,∴∠CAD=30°,
∴∠BAC=45°﹣30°=15°.
故∠BAC=75°或15°.
9.解:如图,过端午A作AH⊥BC于H,过点C作CE⊥AD于E,连接AC.
在Rt△ABH中,tanB==,
∴可以假设AH=3k,BH=4k,则AB=5k=10,
∴k=2,
∴AH=6,BH=8,
∵BC=12,
∴CH=BC﹣BH=12﹣8=4,
∴AC===2,
∵∠B+∠D=90°,∠D+∠ECD=90°,
∴∠ECD=∠B,
在Rt△CED中,tan∠ECD==,
∵CD=5,
∴DE=3,CE=4,
∴AE===6,
∴AD=AE+DE=9.
故答案为:9.
10.解:①当∠ACB为锐角时,如图1,过点A作AD⊥BC,垂足为D,
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD+DC=6+2=8;
②当∠ACB为钝角时,如图2,过点A作AD⊥BC,交BC的延长线于点D,
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD﹣DC=6﹣2=4;
因此BC的长为8或4,
故答案为:8或4.
11.解:如图,取格点K,连接AK,BK.
观察图形可知AK⊥BK,BK=2AK,BK∥CD,
∴∠AED=∠ABK,
∴tan∠AED=tan∠ABK==,
故选:B.
12.解:如图,延长AD到M,使得DM=DF,连接BM.
∵BD=DC,∠BDM=∠CDF,DM=DF,
∴△BDM≌△CDF(SAS),
∴CF=BM=9,∠M=∠CFD,
∵CE∥BM,
∴∠AFE=∠M,
∵EA=EF,
∴∠EAF=∠EFA,
∴∠BAM=∠M,
∴AB=BM=9,
∵AE=4,
∴BE=5,
∵∠EBC=90°,
∴BC===12,
∴AC===15,
∴cos∠ACB===,
解法二:过点D作DG平行AC,构造三角形BDG相似于三角形BCG,同理AEF相似于AGD,再由题目条件,可得cos角ACB的值,遇到分点问题想平行,构造A或8字型相似.
故选:D.
13.解:(1)过点C作CG⊥AB,垂足为G,
∵∠ACB=90°,
∴∠ACG=∠B,
在△ABC中,sinB=,设AC=3x,则AB=5x,BC=4x,
∴sin∠ACG===sinB,
∴AG=x,CG=x,
∴DG=DA+AG=3x+x=x,
在Rt△DCG中,tan∠D==;
(2)过点C作CH∥DB,交BF的延长线于点H,则有△CHF∽△DBF,
又有E是AC的中点,可证△CHE≌△ABE,
∴HC=AB=5x,
由△CHF∽△DBF得:===.
14.解:(1)如图,
由勾股定理得:AB==2,
AC==3,BC==,
∴AB2+AC2=(2)2+(3)2=26,
BC2=()2=26,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
tan∠ACB===;
(2)如图,∵S△DEF=×2×3=3,
∵BC=,CD==,BD==,
∴BC2+CD2=52,BD2=52,
∴BC2+CD2=BD2,
∴∠BCD=90°,BC=CD,
∴∠CBD=45°,
∴CD=.
15.解:设直线AB交CE于点H,BD交CE于点N,
设∠E=α,则cos∠E==cosα,则sinα=,tanα=4,
∵tan∠ABD=,则tan∠BHN=2,
∵AE⊥AC,BC⊥AC,
∴AE∥BC,
∴∠E=∠ECB=α,
∵∠NDC+∠NCD=90°,∠NCB+∠NCD=90°,
∴∠NCB=∠NDC=α,
在△AHE中,设AE=a,则AG=AEsinα=asinα,GE=acosα,
则GH===AG=asinα,则EH=GE+GH=acosα+asinα,
在Rt△AEC中,EC==,
则HC=EC﹣EH=﹣(acosα+asinα);
在△BHC中,tan∠BHN=2,tanα=4,HC=﹣(acosα+asinα),
同理可得:BC=×,
在Rt△BCD中,CD==×=a(﹣﹣)=,
AD=AC﹣CD=4a﹣=,
则=,故答案为.
二.解直角三角形的应用
16.解:∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=60°,
∴∠ABD=60°﹣30°=30°,
∴∠A=∠ABD,
∴BD=AD=20米,
∴BC=BD sin60°=10(米),故选:C.
17.解:在Rt△ABC中,∵∠A=90°,BC=3.5米,∠BCA=29°,
∴AB=BC sin∠ACB=3.5 sin29°,
故选:A.
18.解:在直角△ADE中,∠DAE=α,AE=5米,tan,
∴tanα===,
∴DE=1.5米.
又CE=AB=1.7米,
∴CD=CE+DE=3.2米.故选:C.
19.解:如图,作OH⊥AB于H.
由题意:AB=8,OA﹣OH=3,
∵OH⊥AB,
∴AH=BH=4,
∵AH2+OH2=OA2,
∴42=(OA+OH)(OA﹣OH),
∴OA+OH=,
∴OA=,OH=,
∴cos∠OAB===,
故选:B.
20.解:设AB=xm,
在Rt△ABD中,∵∠ADB=45°,
∴AB=BD=xm,
在Rt△ABC中,∵∠ACB=56.3°,且tan∠ACB=,
∴BC==≈x,
由BC+CD=BD得x+10=x,
解得x=30,
∴AB的长约为30m,
故选:B.
21.解:∵动力×动力臂=阻力×阻力臂,
∴当阻力及阻力臂不变时,动力×动力臂为定值,且定值>0,
∴动力随着动力臂的增大而减小,
∵杠杆向下运动时α的度数越来越小,此时cosα的值越来越大,而β的度数越来越大,cosβ的值越来越小,
∴阻力臂越来越小,而阻力不变,
∴动力×动力臂越来越小,而动力臂越来越大,
∴此时的动力越来越小,
故选:A.
22.解:如图,∵CE∥AB,
∴∠ECB=∠ABC,
∵∠ECB=∠ACB,
∴∠ACB=∠ABC,
∴AC=AB,
作CD⊥AB,垂足为D,
则CD=1.
∵sin∠A=,
∴==AB,
∴S△ABC=×AB×CD=,
∴折叠后重叠部分的面积为cm2.
故选:D.
23.解:由题意可得:∵AM=4米,∠MAD=45°,
∴DM=4m,
∵AM=4米,AB=8米,
∴MB=12米,
∵∠MBC=30°,
∴BC=2MC,
∴MC2+MB2=(2MC)2,
MC2+122=(2MC)2,
∴MC=4,
则DC=4﹣4≈2.9(米),
故答案为:2.9.
24.解:如图②中,过点D作DH⊥AC于H,
在Rt△ADH中,cos∠CAD=,sin∠CAD=,
∴AH=AD cos53°≈25×=15(m),DH=AD sin53°≈25×=20(m),
∵AC=20m,
∴CH=AC﹣AH=5(m),
∴CD===5(m).
25.解:(1)在Rt△ABC中,
∵∠BAC=64°,AC=5m,
∴AB=≈5÷0.44≈11.4(m);
故答案为:11.4;
(2)过点D作DH⊥地面于H,交水平线于点E,
在Rt△ADE中,
∵AD=20m,∠DAE=64°,EH=1.5m,
∴DE=sin64°×AD≈20×0.9≈18(m),
即DH=DE+EH=18+1.5=19.5(m),
答:如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是19.5m.
26.解:(1)在Rt△EFH中,cos∠FHE===,
∴∠FHE=45°.
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan60°=1.3×=1.3(米),
∴GM=AB=1.3(米),
在Rt△ANH中,∠FAN=∠FHE=45°,
∴HN=AHsin45°=×=(米),
∴EM=EG+GM=+1.3≈2.75(米).
答:篮板底部点E到地面的距离大约是2.75米.
27.解:过点C作CE⊥PB,垂足为E,过点D作DF⊥PB,垂足为F,
则∠CEP=∠PFD=90°,
由题意可知:设AB=x,
在Rt△PCE中,tan32.3°=,
∴PE=x tan32.3°,
同理可得:在Rt△PDF中,tan55.7°=,
∴PF=x tan55.7°,
由PF﹣PE=EF=CD=35,
可得x tan55.7°﹣x tan32.3°=35,
解得:x=42.
∴楼间距AB的长度约为42m.
28.解:∵CD⊥AC,
∴∠ACD=90°,
∵∠ABD=135°,
∴∠DBC=45°,
∴∠D=45°,
∴CB=CD,
在Rt△DCB中:CD2+BC2=BD2,
2CD2=8002,
CD=400≈566(米),
答:直线L上距离D点566米的C处开挖.
29.解:(1)当∠ANB=45°时,
∵MB=MN,
∴∠B=∠ANB=45°,
∴∠NMB=180°﹣∠ANB﹣∠B=90°.
在Rt△NMB中,sin∠B=,
∴BN===12cm.
∴CN=CB﹣BN=AN﹣BN=(20﹣12)cm.
(2)当∠ANB=30°时,作ME⊥CB,垂足为E.
∵MB=MN,
∴∠B=∠ANB=30°
在Rt△BEM中,cos∠B=,
∴BE=MB cos∠B=(AN﹣AM) cos∠B=6cm.
∵MB=MN,ME⊥CB,
∴BN=2BE=12cm.
∵CB=AN=20cm,且12>20,
∴此时N不在CB边上,与题目条件不符.
随着∠ANB度数的减小,BN长度在增加,
∴倾斜角不可以小于30°.
三.解直角三角形的应用-坡度坡角问题
30.解:延长AB交ED于G,过C作CF⊥DE于F,
∴GF=BC=5(米),
∵山坡CD的坡度为1:0.75,
∴设DF=3k,CF=4k,
∴CD=5k=35(米),
∴k=7(米),
∴DF=21米,BG=CF=28米,
∴EG=GF+DF+DE=5+21+19=45(米),
∵∠AED=52°,
∴AG=EG tan52.5°≈45×1.30=58.5(米),
∴AB=30.5米,
答:铁塔AB的高度约为30.5米.
故选:C.
31.解:过B作BE⊥AD于E,过C作CF⊥AD于F,如图所示:
则四边形BEFC是矩形,
∴BE=CF,
∵背水坡CD的坡比i=1:1,CD=米,
∴CF=DF=CD=6(米),
∴BE=CF=6米,
又∵斜坡AB的坡比i=1:2=,
∴AE=2BE=12(米),
∴AB===6(米),
故选:C.
32.解:Rt△ABC中,tan∠BAC=斜坡AB的坡度=1:=,
∴∠BAC=30°,
∵BC⊥AC,
∴BC=AB=3m,
故选:B.
33.解:如图AC=13,作CB⊥AB,
∵sinα==,
∴BC=5,
∴小车上升的高度是5m.
故选:A.
34.解:∵斜面坡度为1:2,BC=6m,
∴AC=12m,
则AB=(m).
故选:B.
35.解:过点A作AD⊥CB延长线于点D,
∵∠ABD=45°,
∴AD=BD,
∵AB=4,
∴AD=BD=ABsin45°=4×=4,
∵坡度i=1:,
∴,
则DC=4,
故AC==8(m).
故选:A.
36.解:∵迎水坡AB的坡比是1:,坝高BC=10m,
∴==,
解得:AC=10,
则AB==20(m).
故答案为:20.
37.解:(1)如图,
在Rt△ABM中,AM=ABsin45°=2(米).
在Rt△ACM中,
∵∠ACM=30°,
∴AC=2AM=4(米).
即新传送带AC的长度约为4米;
(2)结论:货物DEFG不用挪走.
解:在Rt△ABM中,BM=ABcos45°=2(米).
在Rt△ACM中,CM=AM=2(米).
∴CB=CM﹣BM=2﹣2≈2.08(米).
∵DC=DB﹣CB≈5﹣2.08=2.92(米)>2(米),
∴货物DEFG不应挪走.
38.解:(1)由题意CD=CH,
在Rt△ACH中,CH==2≈12.2(cm).
∴CD=CH=12.2(cm).
(2)如图2中,过点E作EK⊥PC于K.
在Rt△ECK中,EK=EC sin53°≈4(cm),CK=EC cos53°≈3(cm),
在Rt△EPK中,PK===2≈4.48(cm),
∴DP=CD﹣CK﹣PK﹣MN=12.2﹣3﹣4.48﹣2=2.72>2.5,
∴能在ND处装入一段长为2.5cm的订书钉.
四.解直角三角形的应用-仰角俯角问题
39.解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC tanα=2tanα,
故选:B.
40.解:连接DE,作BF⊥DE于F,BG⊥DA于G,如图:
则DF=BG,BF=DG=AD+AG,
∵AB=斜坡AB的坡度i=0.75=,
∴设BG=3xm,则AG=4xm,BF=DG=20+4x(m),CF=BF+BC=20+4x+20=40+4x(m),
由题意得:∠EBF=37°,∠ECF=22°,
∵tan∠BEF==,tan∠ECF==,
∴EF=tan37°(20+4x),EF=tan22°(40+4x),
∴0.75(20+4x)=0.40(40+4x),
解得:x=,
∴DF=BG=3x=(m),
EF=0.40(40+4x)=(m),
∴DE=DF+EF=+≈19.3(m);
故选:B.
41.解:∵AB⊥BE,DE⊥BE,AD∥BE,
∴四边形ABED是矩形,
∵BE=9m,AB=1.5m,
∴AD=BE=9m,DE=AB=1.5m,
在Rt△ACD中,
∵∠CAD=30°,AD=9m,
∴CD=AD tan30°=9×=3,
∴CE=CD+DE=3+1.5
故选:C.
42.解:延长PQ交直线AB于点E,设PE=x米.
在直角△APE中,∠A=45°,
则AE=PE=x米;
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中,BE=PE=x米,
∵AB=AE﹣BE=6米,
则x﹣x=6,
解得:x=9+3.
则BE=(3+3)米.
在直角△BEQ中,QE=BE=(3+3)=(3+)米.
∴PQ=PE﹣QE=9+3﹣(3+)=6+2(米).
答:电线杆PQ的高度是6+2(米).
故选:A.
43.解:∵∠BCD=∠BAC+∠ABC,∠BAC=30°,∠BCD=60°,
∴∠ABC=∠BCD﹣∠BAC=30°,
∴∠BAC=∠ABC,
∴BC=AC=6m,
在Rt△BDC中,
∵BD=BC sin∠BCD=6×=3(m),
故答案为:3.
44.解:由题意可得:tan30°===,
解得:BD=20(米),
tan60°===,
解得:DC=60(米),
故该建筑物的高度为:BC=BD+DC=80(米)
故答案为80.
45.解:由题意可得:∠BDA=45°,
则AB=AD,
又∵∠CAD=30°,
∴在Rt△ADC中,CD=45m.
tan∠CDA=tan30°==,即=,
解得:AD=45(m),
∴AB=45m.
故答案为:45.
46.解:如图,过点D作DK⊥BC于K,DH⊥CE于H,
则四边形DHCK为矩形.
故DK=CH,CK=DH,
在直角三角形AHD中,=,AD=2米,
∴DH=2米,AH=4米,
∴CK=DH=2米,
设BC=x米,
在直角三角形ABC中,AC==x米,
∴DK=(4+x)米,BK=(x﹣2)米,
在直角三角形BDK中,∵BK=DK tan30°,
∴x﹣2=(4+x)×,
解得:x=5+3,
∴BC=(5+3 )米.
答:大树的高度为(3+5)米.
故答案是:2;(3+5).
47.解:如图所示:过点B作BN⊥AE,CM⊥DE垂足分别为:N,M,
∵i=1:2.4,AB=26m,
∴设BN=x,则AN=2.4x,
∴AB=2.6x,
则2.6x=26,
解得:x=10,
故BN=10,
∴CN=ME=11.6,
则tan30°===,
解得:CM=11.6,
则tan37°===0.75,
解得:DM≈15.1(m),
故DE=DM+EM=15.1+11.6=26.7(m).
故选:C.
五.解直角三角形的应用-方向角问题
48.解:如图所示:
由题意可知∠NPA=55°,PA=6海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=55°.
在Rt△ABP中,∵∠ABP=90°,∠A=55°,PA=6海里,
∴AB=AP cos∠A=6cos55°海里.
故选:B.
49.解:在Rt△PQT中,
∵∠QPT=90°,∠PQT=90°﹣70°=20°,
∴∠PTQ=70°,
∴tan70°=,
∴PT==,
即河宽米,
故选:B.
50.解:作CD⊥AB于点D,垂足为D,
在Rt△BCD中,
∵BC=12×1.5=18(海里),∠CBD=45°,
∴CD=BC sin45°=18×=9(海里),
则在Rt△ACD中,
AC==9×2=18(海里).
故我渔政船航行了18海里.
故答案为:18.
51.解:(1)如图所示:延长BA,过点C作CD⊥BA延长线于点D,
由题意可得:∠CBD=30°,BC=120海里,
则CD=BC=60海里,
∵cos∠ACD==cos30°=,
即=,
∴AC=40(海里),
答:此时点A到军港C的距离为40海里;
(2)过点A′作A′N⊥BC于点N,如图:
由(1)得:CD=60海里,AC=40海里,
∵A'E∥CD,
∴∠AA'E=∠ACD=30°,
∴∠BA′A=45°,
∵∠BA'E=75°,
∴∠ABA'=15°,
∴∠2=15°=∠ABA',
即A′B平分∠CBA,
∴A'E=A'N,
设AA′=x,则AE=AA',A'N=A′E=AE=x,
∵∠1=60°﹣30°=30°,A'N⊥BC,
∴A'C=2A'N=x,
∵A'C+AA'=AC,
∴x+x=40,
解得:x=60﹣20,
∴AA'=(60﹣20)海里,
答:此时渔船的航行距离为(60﹣20)海里.
52.解:(1)由题意得:∠BAC=90°﹣60°=30°,∠MBC=90°﹣30°=60°,
∵∠MBC=∠BAC+∠ACB,
∴∠ACB=∠MBC﹣∠BAC=30°,
∴∠BAC=∠ACB,
∴BC=AB=24×=12(海里);
(2)该货船无触礁危险,理由如下:
过点C作CD⊥AD于点D,如图所示:
∵∠EAC=60°,∠FBC=30°,
∴∠CAB=30°,∠CBD=60°.
∴在Rt△CBD中,CD=BD.
在Rt△CAD中,AD=CD=3BD=AB+BD=12+BD,
∴BD=6.
∴CD=6.
∵6>9,
∴货船继续向正东方向行驶无触礁危险.
53.解:如图,作PD⊥AB交AB延长线于D点,
∵∠PBC=30°,
∴∠PAB=15°,
∴∠APB=∠PBC﹣∠PAB=15°,
∴PB=AB=20×2=40 (海里),
在Rt△BPD中,
∴PD=PB=20(海里),
∵20>18,
∴不会触礁.
54.解:过P作PC⊥AB于点C,
∴∠ACP=90°.
由题意可知,∠PAC=30°,∠PBC=45°.
∴∠BPC=45°.
∴BC=PC.
在Rt△ACP中,.
∵AB=20,
∴.
∴≈27.3.
答:河流宽度约为27.3米.
55.解:(1)过B作BM⊥AC于M,
由题意可知∠BAM=45°,则∠ABM=45°,
在Rt△ABM中,∵∠BAM=45°,AB=40nmile,
∴BM=AM=AB=20nmile,
∴渔船航行20nmile距离小岛B最近;
(2)∵BM=20nmile,MC=20nmile,
∴tan∠MBC===,
∴∠MBC=60°,
∴∠CBG=180°﹣60°﹣45°﹣30°=45°,
在Rt△BCM中,∵∠CBM=60°,BM=20nmile,
∴BC==2BM=40nmile,
故救援队从B处出发沿点B的南偏东45°的方向航行到达事故地点航程最短,最短航程是40nmile.
56.解:(1)∵∠MAC=60°,
∴∠BAC=30°,
又∵BP⊥AC,
∴∠APB=90°,
∴∠ABP=60°,
又∵∠CBN=29°,∠ABN=90°,
∴∠ABC=119°,
∴∠PBC=∠ABC﹣∠ABP=59°;
(2)不会受到影响.理由如下:
由(1)可知,∠PBC=59°,
∴∠C=90°﹣∠PBC=31°,
又∵tan31°=0.60,
∴,
设BP为x海里,
则AP=海里,CP=海里,
∴,
解得:x≈59,
∵59>50,
∴沿海城市B不会受到台风影响.
