2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用同步达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用同步达标测评(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 549.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 12:35:29 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》
同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为( )
A. B. C. D.
2.如图,在△ABC中,∠ABC=90°,tan∠BAC=,AD=2,BD=4,连接CD,则CD长的最大值是( )
A.2+ B.2+1 C.2+ D.2+2
3.如图,在△ABC中,∠ABC=90°,D为BC的中点,点E在AB上,AD,CE交于点F,AE=EF=4,FC=9,则cos∠ACB的值为( )
A. B. C. D.
4.已知△ABC中,BC=a,AC=b,AB=c,且2b=a+c,延长CA到D,使AD=AB,连接BD,则tan∠BCA的值为( )
A. B. C. D.
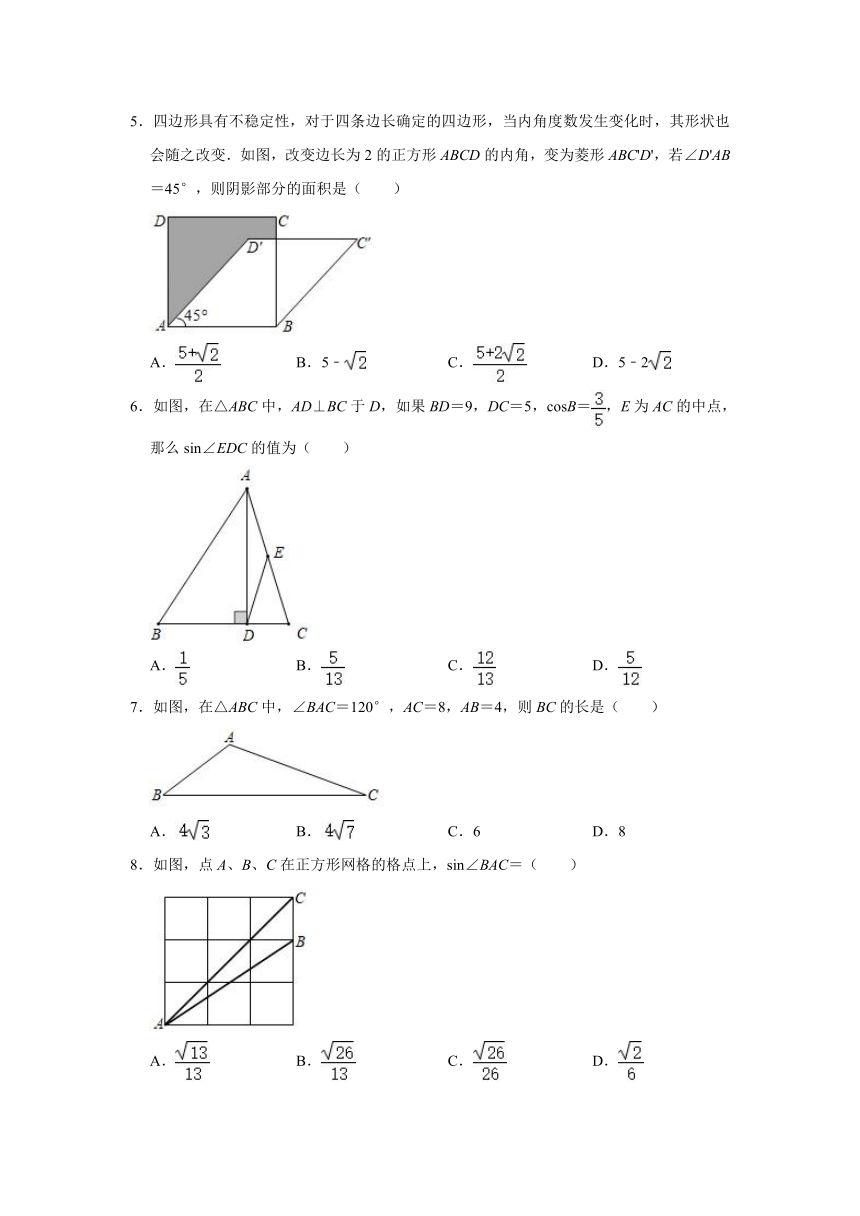
5.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变边长为2的正方形ABCD的内角,变为菱形ABC'D',若∠D'AB=45°,则阴影部分的面积是( )
A. B.5﹣ C. D.5﹣2
6.如图,在△ABC中,AD⊥BC于D,如果BD=9,DC=5,cosB=,E为AC的中点,那么sin∠EDC的值为( )
A. B. C. D.
7.如图,在△ABC中,∠BAC=120°,AC=8,AB=4,则BC的长是( )
A. B. C.6 D.8
8.如图,点A、B、C在正方形网格的格点上,sin∠BAC=( )
A. B. C. D.
9.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,AD=3,CE=5,则tan∠BCE的值为( )
A. B. C. D.
10.在△ABC中,如果sinA=,cotB=,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
二.填空题(共5小题,满分20分)
11.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图,在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°====2﹣.类比这种方法,计算tan22.5°的值为 .
12.关于x的方程2x2﹣5xsinA+2=0有两个相等的实数根,其中∠A是锐角△ABC的一个内角;关于y的方程y2﹣10y+m2﹣4m+29=0的两个根恰好是△ABC的两边长,则△ABC的周长是 .
13.如图,在△ABC中,∠A=90°,AB=22021,AC=22020,点D1,D3,D5,…D2n﹣1在AB边上,点D2,D4,D6,…D2n在AC边上,若∠B=∠ACD1=∠AD1D2=∠AD2D3=…=∠ADnDn+1,则D2020D2021= .
14.如图,已知点A(4,3),点B为直线y=﹣2上的一动点,点C(0,n),﹣2<n<3,AC⊥BC于点C,连接AB.若直线AB与x轴正半轴所夹的锐角为α,那么当sinα的值最大时,n的值为 .
15.如图,每个小正方形的边长都为1,点A、B、C都在小正方形的顶点上,则∠ABC的正切值为 .
三.解答题(共10小题,满分70分)
16.为方便市民绿色出行,临沂市政府推出共享单车服务.图①是某品牌共享单车放在地面上的实物图,图②是其示意图,其中AB、CD均与地面l平行,车轮半径为32cm,∠BCD=64°,BC=60cm,坐垫E与点B的距离BE为15cm.
(1)求坐垫E到地面的距离;
(2)根据经验,当坐垫E到CD的距离为人体腿长的0.8时,坐骑比较舒适.小明的腿长约78cm,现将坐垫E调整至坐骑舒适高度E',求EE'的长.(结果精确到0.1m,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
17.如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD⊥AO时,称点P为“最佳视角点”,作PC⊥BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若∠AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据:≈1.414,≈1.732)
18.如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了130米到达B处,测的∠CBN=60°,求河流的宽度CE(结果保留整数).
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,≈1.7)
19.某学校部分平面图如图所示,点A,C,D在同一直线上,点B,C,E在同一直线上,∠DAB=∠E=90°,∠ABC=37°.测得A处与D处之间的距离为80米,B处与E处之间的距离为100米,求教学楼D处到实验楼E处的距离(结果保留整数,参考数据:sin37°≈,cos37°≈,tan37°≈)
20.我市里运河有一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.(参考数据:≈1.414,≈1.732)
21.如图,斜坡AF的坡度为5:12,斜坡AF上一棵与水平面垂直的大树BD在阳光照射下,在斜坡上的影长BC=6.5米,此时光线与水平线恰好成30°角,求大树BD的高.(结果精确的0.1米,参考数据≈1.414,≈1.732)
22.阅读材料:关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ,tan(α+β)=.利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和(差),如tan75°=tan(30°+45°)==2+.
问题解决:根据以上阅读材料,请选择适当的公式解答下列问题.
(1)求sin75°;
(2)如图,边长为2的正△ABC沿直线滚动,设当△ABC滚动240°时,C点的位置在C′,当△ABC滚动480°时,A点的位置在A′.
①求tan∠CAC′的值;
②试确定∠CAC′+∠CAA′的度数.
23.已知,如图,四边形ABCD中,AB=BC=1,CD=,DA=1,且∠B=90°.试求:
(1)∠BAD的度数;
(2)四边形ABCD的面积(结果保留根号).
24.某海域有一小岛P,在以P为圆心,半径r为10(3+)海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东60°的方向上,当海监船行驶20海里后到达B处,此时观测小岛P位于B处北偏东45°方向上.
(1)求A,P之间的距离AP;
(2)若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?
25.风能作为一种清洁能源越来越受到世界各国的重视,我省多地结合自身地理优势架设风力发电机利用风能发电.王芳和李华假期去大理巍山游玩,看见风电场的各个山头上布满了大大小小的风力发电机,好奇的想知道风力发电机塔架的高度.如图,王芳站在坡度i=:1,坡面长30m的斜坡BC的底部C点测得C点与塔底D点的距离为25m,此时,李华在坡顶B点测得轮毂A点的仰角α=38°,请根据测量结果帮他们计算风力发电机塔架AD的高度.(结果精确到0.1m,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,≈1.41,≈1.73)
参考答案
一.选择题(共10小题,满分30分)
1.解:连接BF,
∵CE是斜边AB上的中线,EF⊥AB,
∴EF是AB的垂直平分线,
∴S△AFE=S△BFE=5,∠FBA=∠A,
∴S△AFB=10=AF BC,
∵BC=4,
∴AF=5=BF,
在Rt△BCF中,BC=4,BF=5,
∴CF==3,
∵CE=AE=BE=AB,
∴∠A=∠FBA=∠ACE,
又∵∠BCA=90°=∠BEF,
∴∠CBF=90°﹣∠BFC=90°﹣2∠A,
∠CEF=90°﹣∠BEC=90°﹣2∠A,
∴∠CEF=∠FBC,
∴sin∠CEF=sin∠FBC==,
故选:A.
2.解:如图,在AD的下方作Rt△ADT,使得∠ADT=90°,DT=1,连接CT,则AT=,
∵==2,
∴=,
∵∠ADT=∠ABC=90°,
∴△ADT∽△ABC,
∴∠DAT=∠BAC,=
∴∠DAB=∠TAC,
∵=,
∴△DAB∽△TAC,
∴==,
∴TC=2,
∵CD≤DT+CT,
∴CD≤1+2,
∴CD的最大值为1+2,
故选:B.
3.解:如图,延长AD到M,使得DM=DF,连接BM.
∵BD=DC,∠BDM=∠CDF,DM=DF,
∴△BDM≌△CDF(SAS),
∴CF=BM=9,∠M=∠CFD,
∵CE∥BM,
∴∠AFE=∠M,
∵EA=EF,
∴∠EAF=∠EFA,
∴∠BAM=∠M,
∴AB=BM=9,
∵AE=4,
∴BE=5,
∵∠EBC=90°,
∴BC===12,
∴AC===15,
∴cos∠ACB===,
解法二:过点D作DG平行AC,构造三角形BDG相似于三角形BCG,同理AEF相似于AGD,再由题目条件,可得cos角ACB的值,遇到分点问题想平行,构造A或8字型相似.
故选:D.
4.解:过点B作BH⊥AC于H,过点B作BH⊥AC于H.
设HC=x,HA=y,HB=h,
∴x2+h2=a2,y2+h2=c2,x+y=b.
解得:x=(5a﹣3c),y=(5c﹣3a),h=(3c﹣a)(3a﹣c).
∵CE=CB,
∴∠E=∠CBE,
∵∠BCA=∠CBE+∠E,
∴∠E=∠BCA,
∴tan∠BAC tan∠BCA=tan∠D tan∠E====.
故选:B.
5.解:设BC与C′D′交点为E,
则BE⊥C′D′,因此C′E=BC′ cosC′,
∵四边形ABC′D′为菱形,则∠C′=∠D′AB=45°,
∴C′E=BC′ cosC′=2×=,
同理BE=BC′ sinC′=,
∴D′E=2﹣,BE=,
∴梯形D′EBA面积为:
S′=(D′E+AB)×BE×=2﹣1,
阴影面积为:S=SSABCD﹣S′
=2×2﹣(2﹣1)
=5﹣2.
故选:D.
6.解:在Rt△ABD中,cosB==,BD=9,
∴AB=BD=15,
由勾股定理得AD===12,
在Rt△ADC中,由勾股定理得AC===13,
∵E为AC中点,
∴ED=EC=AC=,
∴sin∠EDC=sinC==.
故选:C.
7.解:如图,过点C作CE⊥BA交BA的延长线于E.
∵∠BAC=120°,
∴∠CAE=180°﹣120°=60°,
∴AE=AC cos60°=4,EC=AC sin60°=4,
∵AB=4,
∴BE=AB+AE=8,
∴BC===4,
故选:B.
8.解:如图,取格点T,连接BT交AC于H,则BH⊥AC,设BH=a,则AH=5a,
在Rt△AHB中,AB===a,
∴sin∠BAC==,
故选:C.
9.解:∵CE是AB边上的中线,CE=5,
∴AE=BE=5,AB=10,
∴∠BCE=∠EBC,
∵AD=3,
∴BD=AB﹣AD=7,DE=AE﹣AD=2,
在Rt△CDE中,由勾股定理得:
CD===,
∴tan∠BCE=tan∠EBC==.
故选:B.
10.解:∵sinA=,cotB=,
∴∠A=30°,∠B=60°,
∴∠C=180°﹣30°﹣60°=90°,
∴△ABC是直角三角形,
故选:D.
二.填空题(共5小题,满分20分)
11.解:如图,在等腰直角△ABC中,∠C=90°,延长CB至点D,使得AB=BD,则∠BAD=∠D.
∵∠ABC=45°,
∴45°=∠BAD+∠D=2∠D,
∴∠D=22.5°,
设AC=1,则BC=1,AB=AC=,
∴CD=CB+BD=CB+AB=1+,
∴tan22.5°=tanD====﹣1.
故答案为:﹣1.
12.解:根据题意得Δ=25sin2A﹣16=0,
∴sin2A=,
∴sinA=﹣或 ,
∵∠A为锐角,
∴sinA=.
由题意知,方程y2﹣10y+m2﹣4m+29=0有两个实数根,
则△≥0,
∴100﹣4(m2﹣4m+29)≥0,
∴﹣(m﹣2)2≥0,
∴(m﹣2)2≤0,
又∵(m﹣2)2≥0,
∴m=2,
把m=2代入方程,得y2﹣10y+25=0,
解得y1=y2=5,
∴△ABC是等腰三角形,且腰长为5.
分两种情况:
当∠A是顶角时:
如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=AC=5.
∵sinA=,
∴AD=3,BD=4,
∴DC=2,
∴BC=2.
∴△ABC的周长为;
当∠A是底角时:
如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=5,
∵sinA=,
∴AD=DC=3,
∴AC=6.
∴△ABC的周长为16,
综合以上讨论可知:△ABC的周长为或16.
故答案是:或16.
13.解:∵∠A=90°,∠B=∠ACD1=∠AD1D2=∠AD2D3=…=∠ADnDn+1,
∴======…=,
∴AD1=AC=22019,
AD2=AD1=22018,
AD3=AD2=22017,
AD4=AD3=22016,
……
AD2020=AD2019=20=1,
AD2021=AD2020=2﹣1=,
在Rt△AD2020D2021中,
AD2020D2021==,
故答案为:.
14.解:过点A作AM⊥y轴于点M,作AN⊥BN交于点N,
∵直线y=﹣2∥x轴,故∠ABN=α,
当sinα的值最大时,则tanα=值最大,
故BN最小,即BG最大时,tanα最大,
即当BG最大时,sinα的值最大,
设BG=y,
则AM=4,GC=n+2,CM=3﹣n,
∵∠ACM+∠MAC=90°,∠ACM+∠BCG=90°,
∴∠CAM=∠BCG,
∴tan∠CAM=tan∠BCG,
∴,即,
∴y=﹣(n﹣3)(n+2),
∵﹣<0,
故当n=(3﹣2)=时,y取得最大值,
故n=,
故答案为:.
15.解:
如图:长方形AEFM,连接AC,
∵由勾股定理得:AB2=32+12=10,BC2=22+12=5,AC2=22+12=5,
∴AC2+BC2=AB2,AC=BC,
即∠ACB=90°,
∴tan∠ABC==1,
故答案为:1.
三.解答题(共10小题,满分70分)
16.解:(1)如图②,过点E作EH⊥CD,垂足为G,交直线l于点H,
∵CD∥l,
∴EH⊥l,
∴GH等于车轮半径32cm.
在Rt△CGE中,,
即,
∴EG=67.50≈67.5(cm).
坐垫E到地面的距离为67.5+32=99.5(cm).
(2)如图②,在BE上取点E',过点E'作E'P⊥CD于点P,
当E'P=78×0.8=62.4时,
在Rt△E'CP中,,
即,
∴E'C≈69.33(cm),
∴E'E=EC﹣E'C=5.67≈5.7(cm)
17.解:(1)当PA=45cm时,连接PO.
∵D为AO的中点,PD⊥AO,
∴PO=PA=45cm.
∵BO=24cm,BC=12cm,∠C=90°,
∴OC=OB+BC=36cm,PC==27cm;
(2)当∠AOC=120°,过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.
在Rt△DOE中,∵∠DOE=60°,DO=AO=12,
∴DE=DO sin60°=6,EO=DO=6,
∴FC=DE=6,DF=EC=EO+OB+BC=6+24+12=42.
在Rt△PDF中,∵∠PDF=30°,
∴PF=DF tan30°=42×=14,
∴PC=PF+FC=14+6=20≈34.6>27,
∴点P在直线PC上的位置上升了,此时PC的长约是34.6cm.
18.解:过点C作CF∥DA交AB于点F.
∵MN∥PQ,CF∥DA,
∴四边形AFCD是平行四边形.
∴AF=CD=50m,∠CFB=35°.
∴FB=AB﹣AF=130﹣50=80(m),
设BE=x,∵∠CBN=60°,
∴EC=x,
∴tan35°=≈0.7,
即=0.7,
解得:x=56,
∴CE=56×1.7≈95.2≈95(m),
答:河流的宽是95米.
19.解:∵∠DAB=∠E=90°,∠ABC=37°,
∴∠D=37°,
根据题意可得:设EC=3x,则DC=5x,DE=4x,
故AC=80﹣5x,BC=100﹣3x,
则sin37°===,
解得:x=,
故DE=4x=25(m),
答:教学楼D处到实验楼E处的距离为25m.
20.解:该文化墙PM不需要拆除,
理由:设新坡面坡角为α,新坡面的坡度为1:,
∴tanα==,
∴α=30°.
作CD⊥AB于点D,则CD=6米,
∵新坡面的坡度为1:,
∴tan∠CAD===,
解得,AD=6,
∵坡面BC的坡度为1:1,CD=6米,
∴BD=6米,
∴AB=AD﹣BD=(6﹣6)米,
又∵PB=8米,
∴PA=PB﹣AB=8﹣(6﹣6)=14﹣6≈14﹣6×1.732≈3.6米>3米,
∴该文化墙PM不需要拆除.
21.解:作CM⊥DB于点M,
∵斜坡AF的坡度是1:2.4,∠A=∠BCM,
∴==,
∴在直角△MBC中,设BM=5x,则CM=12x.
由勾股定理可得:BM2+CM2=BC2,
∴(5x)2+(12x)2=6.52,
解得:x=,
∴BM=5x=,CM=12x=6,
在直角△MDC中,∠DCM=∠EDG=30°,
∴DM=CM tan∠DCM=6tan30°=6×=2,
∴BD=DM+BM=+2≈2.5+2×1.732≈6.0(米).
答:大树的高约为6.0米.
22.解:(1)sin75°=sin(30°+45°)
=sin30° cos45°+cos30° sin45°
=+
=;
(2)①过C′作C′E⊥l于E,
∵△ABC是等边三角形且边长为2,
∴C′E=,AE=2+2+1=5,
∴tan∠CAC′==;
②过A′作A′F⊥l于F,
∵△ABC是等边三角形且边长为2,
∴A′F=,AF=2+2+2+2+1=9,
∴tan∠CAA′==.
设∠CAC′=α,∠CAA′=β,
tan(α+β)===,
∴α+β=30°,
∴∠CAC′+CAA′=30°.
23.解:(1)如图,连接AC,
∵AB=BC=1,且∠B=90°,
∴∠BAC=45°,AC==,
而CD=,DA=1,
∴CD2=AD2+AC2,
∴△ACD是直角三角形,即∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=135°;
(2)∵S四边形ABCD=S△ABC+S△ACD,
而S△ABC=AB×BC=,
S△ACD=AD×CA=,
∴S四边形ABCD=S△ABC+S△ACD=(+1).
24.解:(1)过点P作PC⊥AB,交AB的延长线于点C,
由题意得,∠PAC=30°,∠PBC=45°,AB=20,
设PC=x,则BC=x,
在Rt△PAC中,
∵tan30°===,
∴x=10+10,
∴PA=2x=20+20,
答:A,P之间的距离AP为(20+20)海里;
(2)因为PC﹣10(3+)=10+10﹣30﹣10=10(+1)(﹣)<0,
所以有触礁的危险;
设海监船无触礁危险的新航线为射线BD,作PE⊥BD,垂足为E,
当P到BD的距离PE=10(3+)海里时,
有sin∠PBE===,
∴∠PBD=60°,
∴∠CBD=60°﹣45°=15°,
90°﹣15°=75°
即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域.
25.解:如图,过点B分别作CD,AD的垂线,垂足分别为E,F.
由题意得,四边形BEDF是矩形,
则BE=DF,BF=ED.
在Rt△BCE中,i=:1,
∴∠BCE=60°.
又∵BC=30m,
∴BE=sin60° BC=15m.
由勾股定理得:EC=15m.
∵CD=25m,
∴ED=EC+CD=15+25=40(m).
∴BF=ED=40m.
在Rt△ABF中,∠ABF=38°,AF=tan∠ABF BF=tan38° 40≈0.78×40=31.2(m).
∴AD=AF+FD≈31.2+15×1.73≈57.2(m).
答:塔架高度AD约为57.2m.
同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为( )
A. B. C. D.
2.如图,在△ABC中,∠ABC=90°,tan∠BAC=,AD=2,BD=4,连接CD,则CD长的最大值是( )
A.2+ B.2+1 C.2+ D.2+2
3.如图,在△ABC中,∠ABC=90°,D为BC的中点,点E在AB上,AD,CE交于点F,AE=EF=4,FC=9,则cos∠ACB的值为( )
A. B. C. D.
4.已知△ABC中,BC=a,AC=b,AB=c,且2b=a+c,延长CA到D,使AD=AB,连接BD,则tan∠BCA的值为( )
A. B. C. D.
5.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变边长为2的正方形ABCD的内角,变为菱形ABC'D',若∠D'AB=45°,则阴影部分的面积是( )
A. B.5﹣ C. D.5﹣2
6.如图,在△ABC中,AD⊥BC于D,如果BD=9,DC=5,cosB=,E为AC的中点,那么sin∠EDC的值为( )
A. B. C. D.
7.如图,在△ABC中,∠BAC=120°,AC=8,AB=4,则BC的长是( )
A. B. C.6 D.8
8.如图,点A、B、C在正方形网格的格点上,sin∠BAC=( )
A. B. C. D.
9.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,AD=3,CE=5,则tan∠BCE的值为( )
A. B. C. D.
10.在△ABC中,如果sinA=,cotB=,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
二.填空题(共5小题,满分20分)
11.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图,在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°====2﹣.类比这种方法,计算tan22.5°的值为 .
12.关于x的方程2x2﹣5xsinA+2=0有两个相等的实数根,其中∠A是锐角△ABC的一个内角;关于y的方程y2﹣10y+m2﹣4m+29=0的两个根恰好是△ABC的两边长,则△ABC的周长是 .
13.如图,在△ABC中,∠A=90°,AB=22021,AC=22020,点D1,D3,D5,…D2n﹣1在AB边上,点D2,D4,D6,…D2n在AC边上,若∠B=∠ACD1=∠AD1D2=∠AD2D3=…=∠ADnDn+1,则D2020D2021= .
14.如图,已知点A(4,3),点B为直线y=﹣2上的一动点,点C(0,n),﹣2<n<3,AC⊥BC于点C,连接AB.若直线AB与x轴正半轴所夹的锐角为α,那么当sinα的值最大时,n的值为 .
15.如图,每个小正方形的边长都为1,点A、B、C都在小正方形的顶点上,则∠ABC的正切值为 .
三.解答题(共10小题,满分70分)
16.为方便市民绿色出行,临沂市政府推出共享单车服务.图①是某品牌共享单车放在地面上的实物图,图②是其示意图,其中AB、CD均与地面l平行,车轮半径为32cm,∠BCD=64°,BC=60cm,坐垫E与点B的距离BE为15cm.
(1)求坐垫E到地面的距离;
(2)根据经验,当坐垫E到CD的距离为人体腿长的0.8时,坐骑比较舒适.小明的腿长约78cm,现将坐垫E调整至坐骑舒适高度E',求EE'的长.(结果精确到0.1m,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
17.如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD⊥AO时,称点P为“最佳视角点”,作PC⊥BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若∠AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据:≈1.414,≈1.732)
18.如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了130米到达B处,测的∠CBN=60°,求河流的宽度CE(结果保留整数).
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,≈1.7)
19.某学校部分平面图如图所示,点A,C,D在同一直线上,点B,C,E在同一直线上,∠DAB=∠E=90°,∠ABC=37°.测得A处与D处之间的距离为80米,B处与E处之间的距离为100米,求教学楼D处到实验楼E处的距离(结果保留整数,参考数据:sin37°≈,cos37°≈,tan37°≈)
20.我市里运河有一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.(参考数据:≈1.414,≈1.732)
21.如图,斜坡AF的坡度为5:12,斜坡AF上一棵与水平面垂直的大树BD在阳光照射下,在斜坡上的影长BC=6.5米,此时光线与水平线恰好成30°角,求大树BD的高.(结果精确的0.1米,参考数据≈1.414,≈1.732)
22.阅读材料:关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ,tan(α+β)=.利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和(差),如tan75°=tan(30°+45°)==2+.
问题解决:根据以上阅读材料,请选择适当的公式解答下列问题.
(1)求sin75°;
(2)如图,边长为2的正△ABC沿直线滚动,设当△ABC滚动240°时,C点的位置在C′,当△ABC滚动480°时,A点的位置在A′.
①求tan∠CAC′的值;
②试确定∠CAC′+∠CAA′的度数.
23.已知,如图,四边形ABCD中,AB=BC=1,CD=,DA=1,且∠B=90°.试求:
(1)∠BAD的度数;
(2)四边形ABCD的面积(结果保留根号).
24.某海域有一小岛P,在以P为圆心,半径r为10(3+)海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东60°的方向上,当海监船行驶20海里后到达B处,此时观测小岛P位于B处北偏东45°方向上.
(1)求A,P之间的距离AP;
(2)若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?
25.风能作为一种清洁能源越来越受到世界各国的重视,我省多地结合自身地理优势架设风力发电机利用风能发电.王芳和李华假期去大理巍山游玩,看见风电场的各个山头上布满了大大小小的风力发电机,好奇的想知道风力发电机塔架的高度.如图,王芳站在坡度i=:1,坡面长30m的斜坡BC的底部C点测得C点与塔底D点的距离为25m,此时,李华在坡顶B点测得轮毂A点的仰角α=38°,请根据测量结果帮他们计算风力发电机塔架AD的高度.(结果精确到0.1m,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,≈1.41,≈1.73)
参考答案
一.选择题(共10小题,满分30分)
1.解:连接BF,
∵CE是斜边AB上的中线,EF⊥AB,
∴EF是AB的垂直平分线,
∴S△AFE=S△BFE=5,∠FBA=∠A,
∴S△AFB=10=AF BC,
∵BC=4,
∴AF=5=BF,
在Rt△BCF中,BC=4,BF=5,
∴CF==3,
∵CE=AE=BE=AB,
∴∠A=∠FBA=∠ACE,
又∵∠BCA=90°=∠BEF,
∴∠CBF=90°﹣∠BFC=90°﹣2∠A,
∠CEF=90°﹣∠BEC=90°﹣2∠A,
∴∠CEF=∠FBC,
∴sin∠CEF=sin∠FBC==,
故选:A.
2.解:如图,在AD的下方作Rt△ADT,使得∠ADT=90°,DT=1,连接CT,则AT=,
∵==2,
∴=,
∵∠ADT=∠ABC=90°,
∴△ADT∽△ABC,
∴∠DAT=∠BAC,=
∴∠DAB=∠TAC,
∵=,
∴△DAB∽△TAC,
∴==,
∴TC=2,
∵CD≤DT+CT,
∴CD≤1+2,
∴CD的最大值为1+2,
故选:B.
3.解:如图,延长AD到M,使得DM=DF,连接BM.
∵BD=DC,∠BDM=∠CDF,DM=DF,
∴△BDM≌△CDF(SAS),
∴CF=BM=9,∠M=∠CFD,
∵CE∥BM,
∴∠AFE=∠M,
∵EA=EF,
∴∠EAF=∠EFA,
∴∠BAM=∠M,
∴AB=BM=9,
∵AE=4,
∴BE=5,
∵∠EBC=90°,
∴BC===12,
∴AC===15,
∴cos∠ACB===,
解法二:过点D作DG平行AC,构造三角形BDG相似于三角形BCG,同理AEF相似于AGD,再由题目条件,可得cos角ACB的值,遇到分点问题想平行,构造A或8字型相似.
故选:D.
4.解:过点B作BH⊥AC于H,过点B作BH⊥AC于H.
设HC=x,HA=y,HB=h,
∴x2+h2=a2,y2+h2=c2,x+y=b.
解得:x=(5a﹣3c),y=(5c﹣3a),h=(3c﹣a)(3a﹣c).
∵CE=CB,
∴∠E=∠CBE,
∵∠BCA=∠CBE+∠E,
∴∠E=∠BCA,
∴tan∠BAC tan∠BCA=tan∠D tan∠E====.
故选:B.
5.解:设BC与C′D′交点为E,
则BE⊥C′D′,因此C′E=BC′ cosC′,
∵四边形ABC′D′为菱形,则∠C′=∠D′AB=45°,
∴C′E=BC′ cosC′=2×=,
同理BE=BC′ sinC′=,
∴D′E=2﹣,BE=,
∴梯形D′EBA面积为:
S′=(D′E+AB)×BE×=2﹣1,
阴影面积为:S=SSABCD﹣S′
=2×2﹣(2﹣1)
=5﹣2.
故选:D.
6.解:在Rt△ABD中,cosB==,BD=9,
∴AB=BD=15,
由勾股定理得AD===12,
在Rt△ADC中,由勾股定理得AC===13,
∵E为AC中点,
∴ED=EC=AC=,
∴sin∠EDC=sinC==.
故选:C.
7.解:如图,过点C作CE⊥BA交BA的延长线于E.
∵∠BAC=120°,
∴∠CAE=180°﹣120°=60°,
∴AE=AC cos60°=4,EC=AC sin60°=4,
∵AB=4,
∴BE=AB+AE=8,
∴BC===4,
故选:B.
8.解:如图,取格点T,连接BT交AC于H,则BH⊥AC,设BH=a,则AH=5a,
在Rt△AHB中,AB===a,
∴sin∠BAC==,
故选:C.
9.解:∵CE是AB边上的中线,CE=5,
∴AE=BE=5,AB=10,
∴∠BCE=∠EBC,
∵AD=3,
∴BD=AB﹣AD=7,DE=AE﹣AD=2,
在Rt△CDE中,由勾股定理得:
CD===,
∴tan∠BCE=tan∠EBC==.
故选:B.
10.解:∵sinA=,cotB=,
∴∠A=30°,∠B=60°,
∴∠C=180°﹣30°﹣60°=90°,
∴△ABC是直角三角形,
故选:D.
二.填空题(共5小题,满分20分)
11.解:如图,在等腰直角△ABC中,∠C=90°,延长CB至点D,使得AB=BD,则∠BAD=∠D.
∵∠ABC=45°,
∴45°=∠BAD+∠D=2∠D,
∴∠D=22.5°,
设AC=1,则BC=1,AB=AC=,
∴CD=CB+BD=CB+AB=1+,
∴tan22.5°=tanD====﹣1.
故答案为:﹣1.
12.解:根据题意得Δ=25sin2A﹣16=0,
∴sin2A=,
∴sinA=﹣或 ,
∵∠A为锐角,
∴sinA=.
由题意知,方程y2﹣10y+m2﹣4m+29=0有两个实数根,
则△≥0,
∴100﹣4(m2﹣4m+29)≥0,
∴﹣(m﹣2)2≥0,
∴(m﹣2)2≤0,
又∵(m﹣2)2≥0,
∴m=2,
把m=2代入方程,得y2﹣10y+25=0,
解得y1=y2=5,
∴△ABC是等腰三角形,且腰长为5.
分两种情况:
当∠A是顶角时:
如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=AC=5.
∵sinA=,
∴AD=3,BD=4,
∴DC=2,
∴BC=2.
∴△ABC的周长为;
当∠A是底角时:
如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=5,
∵sinA=,
∴AD=DC=3,
∴AC=6.
∴△ABC的周长为16,
综合以上讨论可知:△ABC的周长为或16.
故答案是:或16.
13.解:∵∠A=90°,∠B=∠ACD1=∠AD1D2=∠AD2D3=…=∠ADnDn+1,
∴======…=,
∴AD1=AC=22019,
AD2=AD1=22018,
AD3=AD2=22017,
AD4=AD3=22016,
……
AD2020=AD2019=20=1,
AD2021=AD2020=2﹣1=,
在Rt△AD2020D2021中,
AD2020D2021==,
故答案为:.
14.解:过点A作AM⊥y轴于点M,作AN⊥BN交于点N,
∵直线y=﹣2∥x轴,故∠ABN=α,
当sinα的值最大时,则tanα=值最大,
故BN最小,即BG最大时,tanα最大,
即当BG最大时,sinα的值最大,
设BG=y,
则AM=4,GC=n+2,CM=3﹣n,
∵∠ACM+∠MAC=90°,∠ACM+∠BCG=90°,
∴∠CAM=∠BCG,
∴tan∠CAM=tan∠BCG,
∴,即,
∴y=﹣(n﹣3)(n+2),
∵﹣<0,
故当n=(3﹣2)=时,y取得最大值,
故n=,
故答案为:.
15.解:
如图:长方形AEFM,连接AC,
∵由勾股定理得:AB2=32+12=10,BC2=22+12=5,AC2=22+12=5,
∴AC2+BC2=AB2,AC=BC,
即∠ACB=90°,
∴tan∠ABC==1,
故答案为:1.
三.解答题(共10小题,满分70分)
16.解:(1)如图②,过点E作EH⊥CD,垂足为G,交直线l于点H,
∵CD∥l,
∴EH⊥l,
∴GH等于车轮半径32cm.
在Rt△CGE中,,
即,
∴EG=67.50≈67.5(cm).
坐垫E到地面的距离为67.5+32=99.5(cm).
(2)如图②,在BE上取点E',过点E'作E'P⊥CD于点P,
当E'P=78×0.8=62.4时,
在Rt△E'CP中,,
即,
∴E'C≈69.33(cm),
∴E'E=EC﹣E'C=5.67≈5.7(cm)
17.解:(1)当PA=45cm时,连接PO.
∵D为AO的中点,PD⊥AO,
∴PO=PA=45cm.
∵BO=24cm,BC=12cm,∠C=90°,
∴OC=OB+BC=36cm,PC==27cm;
(2)当∠AOC=120°,过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.
在Rt△DOE中,∵∠DOE=60°,DO=AO=12,
∴DE=DO sin60°=6,EO=DO=6,
∴FC=DE=6,DF=EC=EO+OB+BC=6+24+12=42.
在Rt△PDF中,∵∠PDF=30°,
∴PF=DF tan30°=42×=14,
∴PC=PF+FC=14+6=20≈34.6>27,
∴点P在直线PC上的位置上升了,此时PC的长约是34.6cm.
18.解:过点C作CF∥DA交AB于点F.
∵MN∥PQ,CF∥DA,
∴四边形AFCD是平行四边形.
∴AF=CD=50m,∠CFB=35°.
∴FB=AB﹣AF=130﹣50=80(m),
设BE=x,∵∠CBN=60°,
∴EC=x,
∴tan35°=≈0.7,
即=0.7,
解得:x=56,
∴CE=56×1.7≈95.2≈95(m),
答:河流的宽是95米.
19.解:∵∠DAB=∠E=90°,∠ABC=37°,
∴∠D=37°,
根据题意可得:设EC=3x,则DC=5x,DE=4x,
故AC=80﹣5x,BC=100﹣3x,
则sin37°===,
解得:x=,
故DE=4x=25(m),
答:教学楼D处到实验楼E处的距离为25m.
20.解:该文化墙PM不需要拆除,
理由:设新坡面坡角为α,新坡面的坡度为1:,
∴tanα==,
∴α=30°.
作CD⊥AB于点D,则CD=6米,
∵新坡面的坡度为1:,
∴tan∠CAD===,
解得,AD=6,
∵坡面BC的坡度为1:1,CD=6米,
∴BD=6米,
∴AB=AD﹣BD=(6﹣6)米,
又∵PB=8米,
∴PA=PB﹣AB=8﹣(6﹣6)=14﹣6≈14﹣6×1.732≈3.6米>3米,
∴该文化墙PM不需要拆除.
21.解:作CM⊥DB于点M,
∵斜坡AF的坡度是1:2.4,∠A=∠BCM,
∴==,
∴在直角△MBC中,设BM=5x,则CM=12x.
由勾股定理可得:BM2+CM2=BC2,
∴(5x)2+(12x)2=6.52,
解得:x=,
∴BM=5x=,CM=12x=6,
在直角△MDC中,∠DCM=∠EDG=30°,
∴DM=CM tan∠DCM=6tan30°=6×=2,
∴BD=DM+BM=+2≈2.5+2×1.732≈6.0(米).
答:大树的高约为6.0米.
22.解:(1)sin75°=sin(30°+45°)
=sin30° cos45°+cos30° sin45°
=+
=;
(2)①过C′作C′E⊥l于E,
∵△ABC是等边三角形且边长为2,
∴C′E=,AE=2+2+1=5,
∴tan∠CAC′==;
②过A′作A′F⊥l于F,
∵△ABC是等边三角形且边长为2,
∴A′F=,AF=2+2+2+2+1=9,
∴tan∠CAA′==.
设∠CAC′=α,∠CAA′=β,
tan(α+β)===,
∴α+β=30°,
∴∠CAC′+CAA′=30°.
23.解:(1)如图,连接AC,
∵AB=BC=1,且∠B=90°,
∴∠BAC=45°,AC==,
而CD=,DA=1,
∴CD2=AD2+AC2,
∴△ACD是直角三角形,即∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=135°;
(2)∵S四边形ABCD=S△ABC+S△ACD,
而S△ABC=AB×BC=,
S△ACD=AD×CA=,
∴S四边形ABCD=S△ABC+S△ACD=(+1).
24.解:(1)过点P作PC⊥AB,交AB的延长线于点C,
由题意得,∠PAC=30°,∠PBC=45°,AB=20,
设PC=x,则BC=x,
在Rt△PAC中,
∵tan30°===,
∴x=10+10,
∴PA=2x=20+20,
答:A,P之间的距离AP为(20+20)海里;
(2)因为PC﹣10(3+)=10+10﹣30﹣10=10(+1)(﹣)<0,
所以有触礁的危险;
设海监船无触礁危险的新航线为射线BD,作PE⊥BD,垂足为E,
当P到BD的距离PE=10(3+)海里时,
有sin∠PBE===,
∴∠PBD=60°,
∴∠CBD=60°﹣45°=15°,
90°﹣15°=75°
即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域.
25.解:如图,过点B分别作CD,AD的垂线,垂足分别为E,F.
由题意得,四边形BEDF是矩形,
则BE=DF,BF=ED.
在Rt△BCE中,i=:1,
∴∠BCE=60°.
又∵BC=30m,
∴BE=sin60° BC=15m.
由勾股定理得:EC=15m.
∵CD=25m,
∴ED=EC+CD=15+25=40(m).
∴BF=ED=40m.
在Rt△ABF中,∠ABF=38°,AF=tan∠ABF BF=tan38° 40≈0.78×40=31.2(m).
∴AD=AF+FD≈31.2+15×1.73≈57.2(m).
答:塔架高度AD约为57.2m.
