2021--2022学年湘教版九年级上册数学第3章 图形的相似 检测试卷 (word版含答案)
文档属性
| 名称 | 2021--2022学年湘教版九年级上册数学第3章 图形的相似 检测试卷 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 86.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 14:05:30 | ||
图片预览


文档简介
湘教版九年级上册数学第3章 图形的相似 检测试卷
(时间:90分钟 满分100分)
学校 班级 姓名 得分
一、选择题(每小题3分,共30分)
1. 下列各组数中,成比例的是( )
A.-7,-5,14,5 B.-6,-8,3,4 C.3,5,9,12 D.2,3,6,12
2.如图,直线 ∥ ∥ ,直线AC分别交 , , 于点A,B,C;直线DF分别交 , , 于点D,E,F.AC与DF相交于点G,且AG=2,GB=1,BC=5,则 的值为( )
A. B. C. D. 2
第2题图 第3题图第4题图
3.如图,在△ABC中,DE∥BC,若=,则=( )
A. B. C. D.
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形有( )
A.1对 B.2对 C.3对 D.4对
5.如图,△ABC∽△DEF,相似比为1∶2,若BC=1,则EF的长是( )
第5题图 第7题图
A. 1 B. 2 C. 3 D. 4
6.已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为( )
A.32 B.8 C.4 D.16
7.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
8.在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( )
第8题图 第10题图
A. 900cm B. 1000cm C. 1100cm D. 1200cm
9.下列说法中:①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A′B′C′D′E′位似,则在五边形中连线组成的△ABC与△A′B′C′也是位似的.正确的个数是( )
A. 1 B. 2 C. 3 D. 4
10.如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长是( )
A. 4或 B. 2或 C.4或 D. 2或
二、填空题(每小题3分,共24分)
11.已知5x-8y=0,则x∶y= .
12.如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3,AD=2,EF=EH,那么EH的长为 .
第12题图 第13题图
13.已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .
14.两三角形的相似比是2:3,则其面积之比是 .
15.在△ABC中,∠B=25°,AD是BC边上的高,并且AD2=BD·DC,则∠BCA的度数为 .
16.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为 .
第16题图 第17题图
17.一块直角三角板ABC按如图放置,顶点A的坐标(0,1),直角顶点C的坐标(-3,0),∠B=30°,则点B的坐标为 .
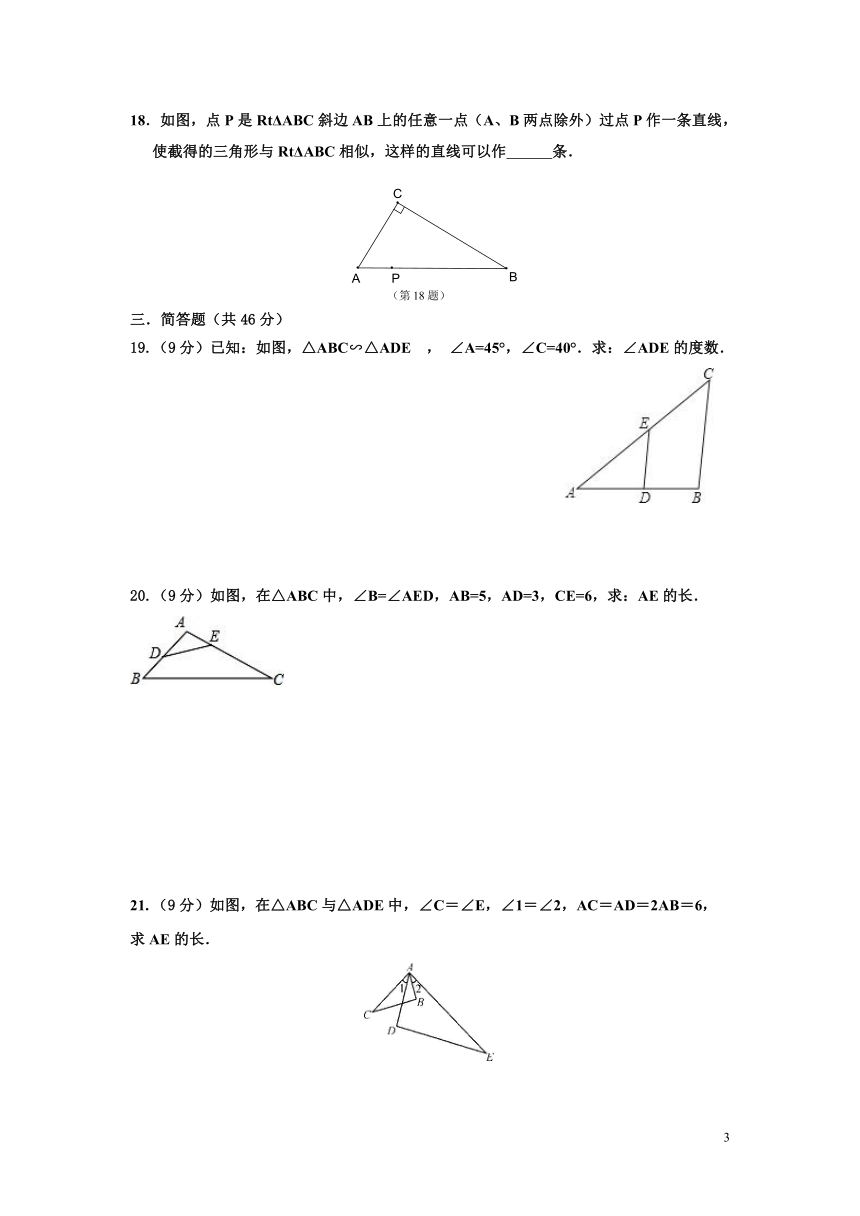
18.如图,点P是RtΔABC斜边AB上的任意一点(A、B两点除外)过点P作一条直线,使截得的三角形与RtΔABC相似,这样的直线可以作 条.
(
(第18题)
)
三.简答题(共46分)
19.(9分)已知:如图,△ABC∽△ADE , ∠A=45°,∠C=40°.求:∠ADE的度数.
20.(9分)如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6,求:AE的长.
(9分)如图,在△ABC与△ADE中,∠C=∠E,∠1=∠2,AC=AD=2AB=6,
求AE的长.
22.(9分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
23.(10分)如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD.
(2)若AB=13,BC=10,求线段DE的长.
答案
一、选择题
1 2 3 4 5 6 7 8 9 10
B B C C B C B D C A
二、填空题
11 12 13 14 15 16 17 18
8∶5 9 4:9 65°或115° 0.4m (-3-,3) 3
19.解:∵△ABC∽△ADE , ∠C=40°,
∴∠AED=∠C=40°.
在△ADE中,
∵∠AED+∠ADE+∠A=180°,∠A=45°
即40°+∠ADE+45°=180°,
∴∠ADE=95°.
20.解:∵∠B=∠AED,∠A=∠A,∴△ADE∽△ABC 则 = ,
即 = .∵AB=5,AD=3,CE=6,∴ = ,∴AE=9
21.解:∵∠1=∠2,∴∠CAB=∠EAD.又∵∠C=∠E,∴△ABC∽△ADE.
∴=.∵AC=AD=2AB=6,∴AB=3.∴=.∴AE=12.
22.解:∵BC∥DE,∴△ABC∽△ADE,∴=,∴=,∴AB=17(m),
经检验:AB=17是分式方程的解,答:河宽AB的长为17米.
23.解:(1)∵AB=AC,BD=CD,
∴AD⊥BC,∠B=∠C,
∵DE⊥AB,
∴∠DEB=∠ADC,
∴△BDE∽△CAD.
(2)∵AB=AC,BD=CD,∴AD⊥BC,
在Rt△ADB中,AD===12,
∵ AD BD= AB DE,∴DE=.
(
1
)
(时间:90分钟 满分100分)
学校 班级 姓名 得分
一、选择题(每小题3分,共30分)
1. 下列各组数中,成比例的是( )
A.-7,-5,14,5 B.-6,-8,3,4 C.3,5,9,12 D.2,3,6,12
2.如图,直线 ∥ ∥ ,直线AC分别交 , , 于点A,B,C;直线DF分别交 , , 于点D,E,F.AC与DF相交于点G,且AG=2,GB=1,BC=5,则 的值为( )
A. B. C. D. 2
第2题图 第3题图第4题图
3.如图,在△ABC中,DE∥BC,若=,则=( )
A. B. C. D.
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形有( )
A.1对 B.2对 C.3对 D.4对
5.如图,△ABC∽△DEF,相似比为1∶2,若BC=1,则EF的长是( )
第5题图 第7题图
A. 1 B. 2 C. 3 D. 4
6.已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为( )
A.32 B.8 C.4 D.16
7.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
8.在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( )
第8题图 第10题图
A. 900cm B. 1000cm C. 1100cm D. 1200cm
9.下列说法中:①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A′B′C′D′E′位似,则在五边形中连线组成的△ABC与△A′B′C′也是位似的.正确的个数是( )
A. 1 B. 2 C. 3 D. 4
10.如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长是( )
A. 4或 B. 2或 C.4或 D. 2或
二、填空题(每小题3分,共24分)
11.已知5x-8y=0,则x∶y= .
12.如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3,AD=2,EF=EH,那么EH的长为 .
第12题图 第13题图
13.已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .
14.两三角形的相似比是2:3,则其面积之比是 .
15.在△ABC中,∠B=25°,AD是BC边上的高,并且AD2=BD·DC,则∠BCA的度数为 .
16.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为 .
第16题图 第17题图
17.一块直角三角板ABC按如图放置,顶点A的坐标(0,1),直角顶点C的坐标(-3,0),∠B=30°,则点B的坐标为 .
18.如图,点P是RtΔABC斜边AB上的任意一点(A、B两点除外)过点P作一条直线,使截得的三角形与RtΔABC相似,这样的直线可以作 条.
(
(第18题)
)
三.简答题(共46分)
19.(9分)已知:如图,△ABC∽△ADE , ∠A=45°,∠C=40°.求:∠ADE的度数.
20.(9分)如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6,求:AE的长.
(9分)如图,在△ABC与△ADE中,∠C=∠E,∠1=∠2,AC=AD=2AB=6,
求AE的长.
22.(9分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
23.(10分)如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD.
(2)若AB=13,BC=10,求线段DE的长.
答案
一、选择题
1 2 3 4 5 6 7 8 9 10
B B C C B C B D C A
二、填空题
11 12 13 14 15 16 17 18
8∶5 9 4:9 65°或115° 0.4m (-3-,3) 3
19.解:∵△ABC∽△ADE , ∠C=40°,
∴∠AED=∠C=40°.
在△ADE中,
∵∠AED+∠ADE+∠A=180°,∠A=45°
即40°+∠ADE+45°=180°,
∴∠ADE=95°.
20.解:∵∠B=∠AED,∠A=∠A,∴△ADE∽△ABC 则 = ,
即 = .∵AB=5,AD=3,CE=6,∴ = ,∴AE=9
21.解:∵∠1=∠2,∴∠CAB=∠EAD.又∵∠C=∠E,∴△ABC∽△ADE.
∴=.∵AC=AD=2AB=6,∴AB=3.∴=.∴AE=12.
22.解:∵BC∥DE,∴△ABC∽△ADE,∴=,∴=,∴AB=17(m),
经检验:AB=17是分式方程的解,答:河宽AB的长为17米.
23.解:(1)∵AB=AC,BD=CD,
∴AD⊥BC,∠B=∠C,
∵DE⊥AB,
∴∠DEB=∠ADC,
∴△BDE∽△CAD.
(2)∵AB=AC,BD=CD,∴AD⊥BC,
在Rt△ADB中,AD===12,
∵ AD BD= AB DE,∴DE=.
(
1
)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
