2021-2022学年湘教版九年级上册数学第4章 锐角三角函数单元检测试卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版九年级上册数学第4章 锐角三角函数单元检测试卷 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 128.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 14:07:31 | ||
图片预览

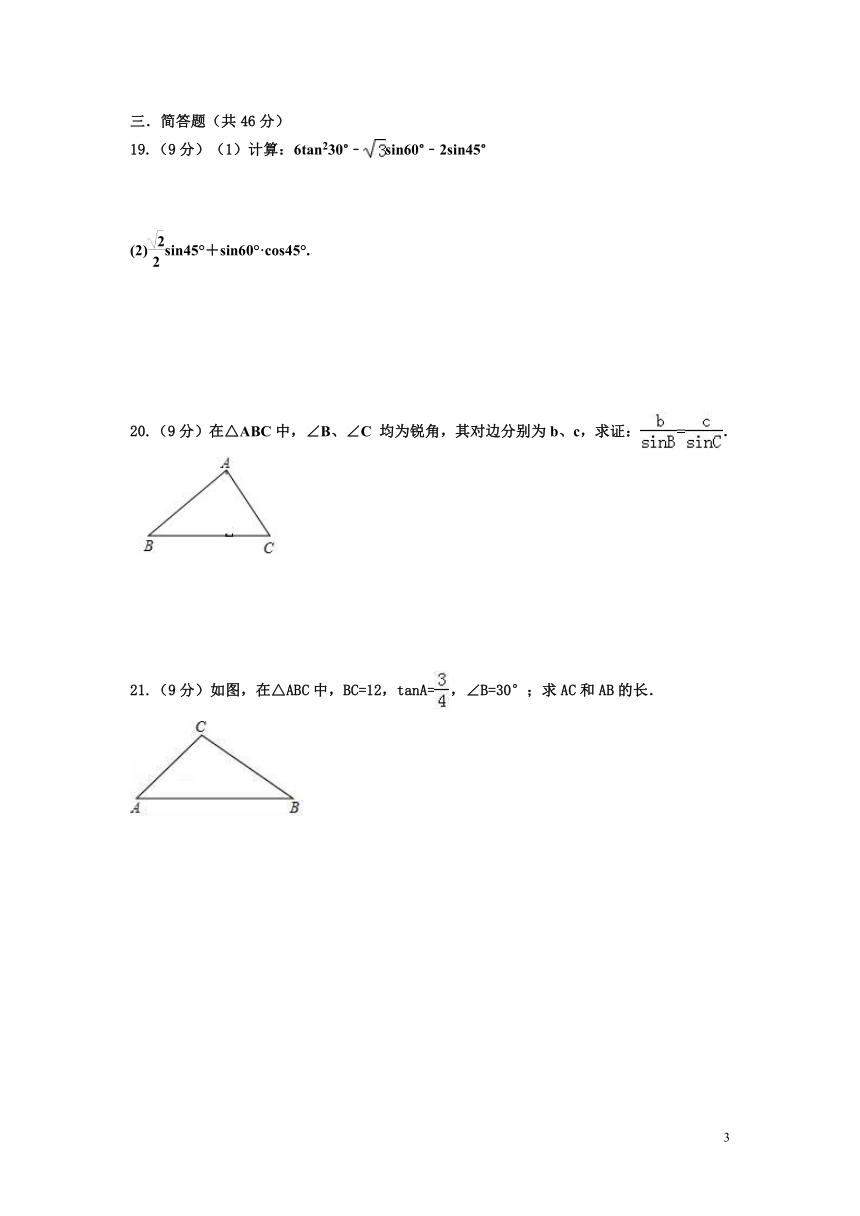
文档简介
湘教版九年级上册数学第4章 锐角三角函数 检测试卷
(时间:90分钟 满分100分)
学校 班级 姓名 得分
一、选择题(每小题3分,共30分)
1.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
第1题图 第2题图
A. B. C. D.
2.如图,将∠AOB放置在5×5的正方形网格中,则tan∠AOB的值是( )
A. B. C. D.
3.在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值 ( )
A 也扩大3倍 B 缩小为原来的 C 都不变 D 有的扩大,有的缩小
4.△ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.bcosB=c B.csinA=a C.atanA=b D.
5.在△ABC中,(2cosA-)2+|1-tanB|=0,则△ABC一定是( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
6.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )
第6题图 第7题图
A.100sin35°米 B.100sin55°米 C.100tan35°米 D.100tan55°米
7.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A. B.1
C. D.
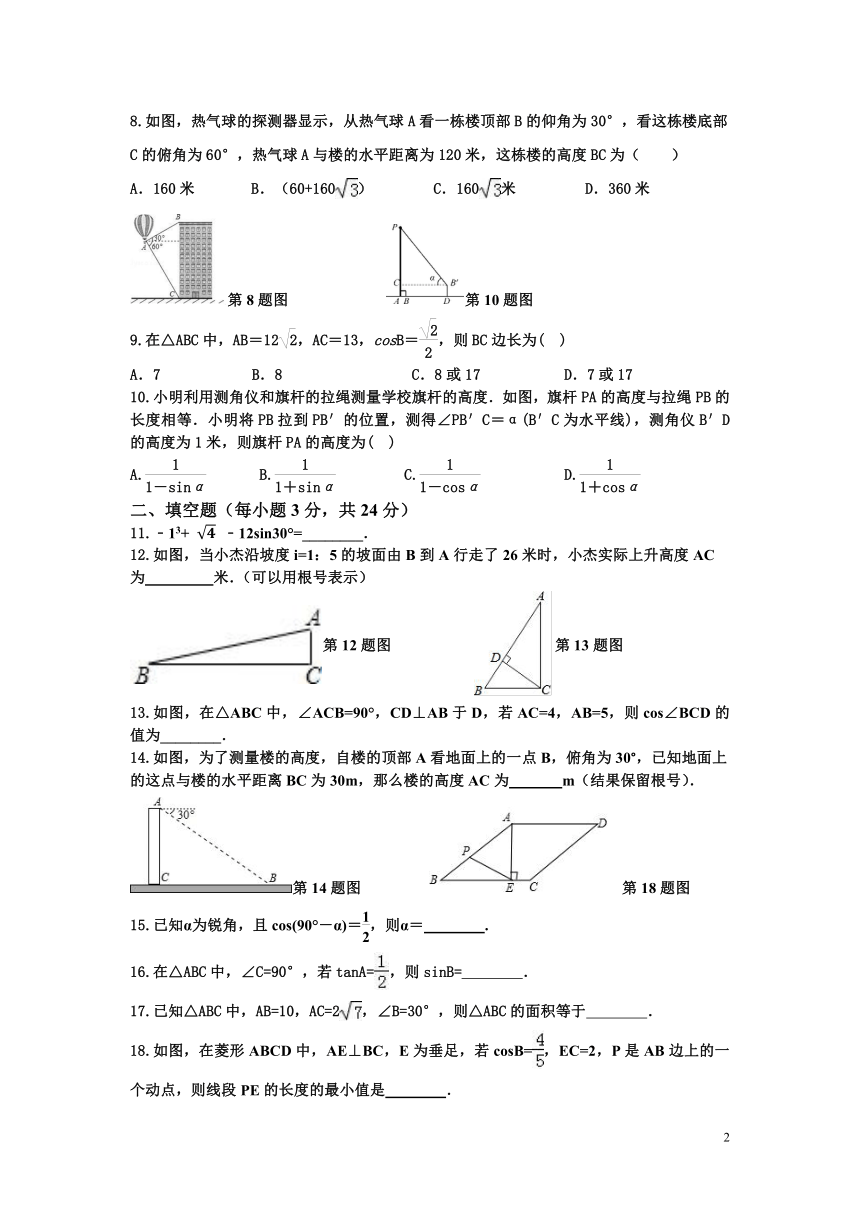
8.如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋楼底部C的俯角为60°,热气球A与楼的水平距离为120米,这栋楼的高度BC为( )
A.160米 B.(60+160) C.160米 D.360米
第8题图 第10题图
9.在△ABC中,AB=12,AC=13,cosB=,则BC边长为( )
A.7 B.8 C.8或17 D.7或17
10.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.﹣13+ ﹣12sin30°=________.
12.如图,当小杰沿坡度i=1:5的坡面由B到A行走了26米时,小杰实际上升高度AC
为 米.(可以用根号表示)
第12题图 第13题图
13.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,AB=5,则cos∠BCD的值为________.
14.如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为 m(结果保留根号).
第14题图 第18题图
15.已知α为锐角,且cos(90°-α)=,则α= .
16.在△ABC中,∠C=90°,若tanA=,则sinB= .
17.已知△ABC中,AB=10,AC=2,∠B=30°,则△ABC的面积等于 .
18.如图,在菱形ABCD中,AE⊥BC,E为垂足,若cosB=,EC=2,P是AB边上的一个动点,则线段PE的长度的最小值是 .
三.简答题(共46分)
19.(9分)(1)计算:6tan230°﹣sin60°﹣2sin45°
(2)sin45°+sin60°·cos45°.
20.(9分)在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
21.(9分)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长.
22.(9分)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)海里处,则海岛A,C之间的距离为多少海里.
(
30
0
45
0
A
r
E
D
B
C
)23. (10分)甲、乙两楼相距45米,从甲楼顶部观测乙楼顶部的俯角为30°,观测乙楼的底部的俯角为45°,试求两楼的高.
答案
一、选择题
1 2 3 4 5 6 7 8 9 10
B B C B D C B C D A
二、填空题
11 12 13 14 15 16 17 18
-5 10 30° 15或10 4.8
19.解:(1)6tan230°﹣sin60°﹣2sin45°
==﹣.
(2)sin45°+sin60°·cos45°.
解:原式=×+×=.
20.证明:过A作AD⊥BC于D,在Rt△ABD中,sinB=,∴AD=ABsinB,
在Rt△ADC中,sinC=,∴AD=ACsinC,∴ABsinB=ACsinC,
而AB=c,AC=b,∴csinB=bsinC,∴=.
21.解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°,∴CH=BC=6,BH==6,
在Rt△ACH中,tanA==,∴AH=8,∴AC==10,∴AB=AH+BH=8+6.
22.解:作AD⊥BC于D,
设AC=x海里,
在Rt△ACD中,AD=AC×sin∠ACD=x,
则CD=x,
在Rt△ABD中,BD=x,
则x+x=18(1+),解得,x=18,
答:A,C之间的距离为18海里.
23.解:解过D做DE⊥AB于E
∵∠MAC=45° ∴∠ACB=45°
BC=45
在RtΔACB中,
在RtΔADE中,∠ADE=30°
答:甲楼高45米,乙楼高米.
(
1
)
(时间:90分钟 满分100分)
学校 班级 姓名 得分
一、选择题(每小题3分,共30分)
1.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
第1题图 第2题图
A. B. C. D.
2.如图,将∠AOB放置在5×5的正方形网格中,则tan∠AOB的值是( )
A. B. C. D.
3.在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值 ( )
A 也扩大3倍 B 缩小为原来的 C 都不变 D 有的扩大,有的缩小
4.△ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.bcosB=c B.csinA=a C.atanA=b D.
5.在△ABC中,(2cosA-)2+|1-tanB|=0,则△ABC一定是( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
6.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )
第6题图 第7题图
A.100sin35°米 B.100sin55°米 C.100tan35°米 D.100tan55°米
7.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A. B.1
C. D.
8.如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋楼底部C的俯角为60°,热气球A与楼的水平距离为120米,这栋楼的高度BC为( )
A.160米 B.(60+160) C.160米 D.360米
第8题图 第10题图
9.在△ABC中,AB=12,AC=13,cosB=,则BC边长为( )
A.7 B.8 C.8或17 D.7或17
10.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.﹣13+ ﹣12sin30°=________.
12.如图,当小杰沿坡度i=1:5的坡面由B到A行走了26米时,小杰实际上升高度AC
为 米.(可以用根号表示)
第12题图 第13题图
13.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,AB=5,则cos∠BCD的值为________.
14.如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为 m(结果保留根号).
第14题图 第18题图
15.已知α为锐角,且cos(90°-α)=,则α= .
16.在△ABC中,∠C=90°,若tanA=,则sinB= .
17.已知△ABC中,AB=10,AC=2,∠B=30°,则△ABC的面积等于 .
18.如图,在菱形ABCD中,AE⊥BC,E为垂足,若cosB=,EC=2,P是AB边上的一个动点,则线段PE的长度的最小值是 .
三.简答题(共46分)
19.(9分)(1)计算:6tan230°﹣sin60°﹣2sin45°
(2)sin45°+sin60°·cos45°.
20.(9分)在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
21.(9分)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长.
22.(9分)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)海里处,则海岛A,C之间的距离为多少海里.
(
30
0
45
0
A
r
E
D
B
C
)23. (10分)甲、乙两楼相距45米,从甲楼顶部观测乙楼顶部的俯角为30°,观测乙楼的底部的俯角为45°,试求两楼的高.
答案
一、选择题
1 2 3 4 5 6 7 8 9 10
B B C B D C B C D A
二、填空题
11 12 13 14 15 16 17 18
-5 10 30° 15或10 4.8
19.解:(1)6tan230°﹣sin60°﹣2sin45°
==﹣.
(2)sin45°+sin60°·cos45°.
解:原式=×+×=.
20.证明:过A作AD⊥BC于D,在Rt△ABD中,sinB=,∴AD=ABsinB,
在Rt△ADC中,sinC=,∴AD=ACsinC,∴ABsinB=ACsinC,
而AB=c,AC=b,∴csinB=bsinC,∴=.
21.解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°,∴CH=BC=6,BH==6,
在Rt△ACH中,tanA==,∴AH=8,∴AC==10,∴AB=AH+BH=8+6.
22.解:作AD⊥BC于D,
设AC=x海里,
在Rt△ACD中,AD=AC×sin∠ACD=x,
则CD=x,
在Rt△ABD中,BD=x,
则x+x=18(1+),解得,x=18,
答:A,C之间的距离为18海里.
23.解:解过D做DE⊥AB于E
∵∠MAC=45° ∴∠ACB=45°
BC=45
在RtΔACB中,
在RtΔADE中,∠ADE=30°
答:甲楼高45米,乙楼高米.
(
1
)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
