3.3 垂径定理 课件(共21张PPT)
文档属性
| 名称 | 3.3 垂径定理 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览




文档简介
(共21张PPT)
§3.3 垂径定理
北师版九年级下册 圆
1.通过手脑结合,充分掌握圆的轴对称性.
2.运用探索、推理,充分了解圆中的垂径定理及其逆定理.
3.拓展思维,与实践相结合,运用垂径定理及其逆定理进行有关的计算和证明.并着重培养学生的数学语言表达能力.
温故知新
圆是轴对称图形吗?
如果是,它的对称轴是什么 你能找到多少条对称轴?
你是用什么方法解决上述问题的
●O
圆的对称轴是任意一条经过圆心的直线,
它有无数条对称轴.
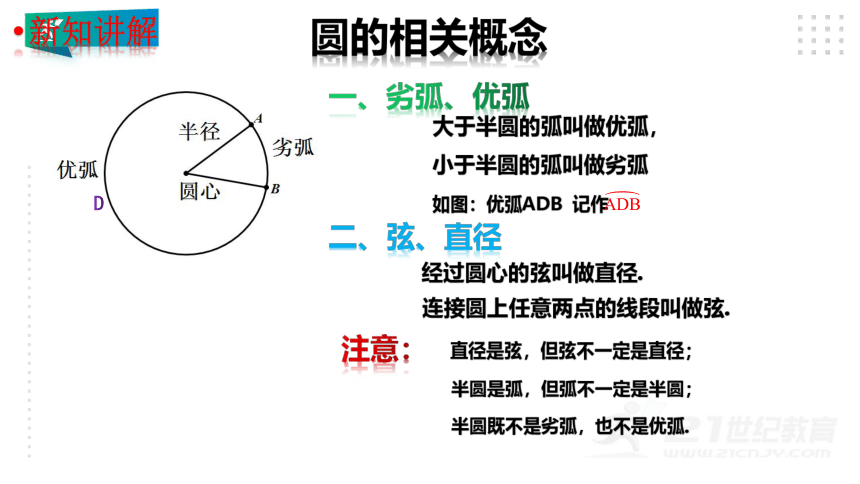
圆的相关概念
新知讲解
大于半圆的弧叫做优弧,
小于半圆的弧叫做劣弧
连接圆上任意两点的线段叫做弦.
经过圆心的弦叫做直径.
直径是弦,但弦不一定是直径;
半圆是弧,但弧不一定是半圆;
半圆既不是劣弧,也不是优弧.
注意:
如图:优弧ADB 记作
一、劣弧、优弧
D
二、弦、直径
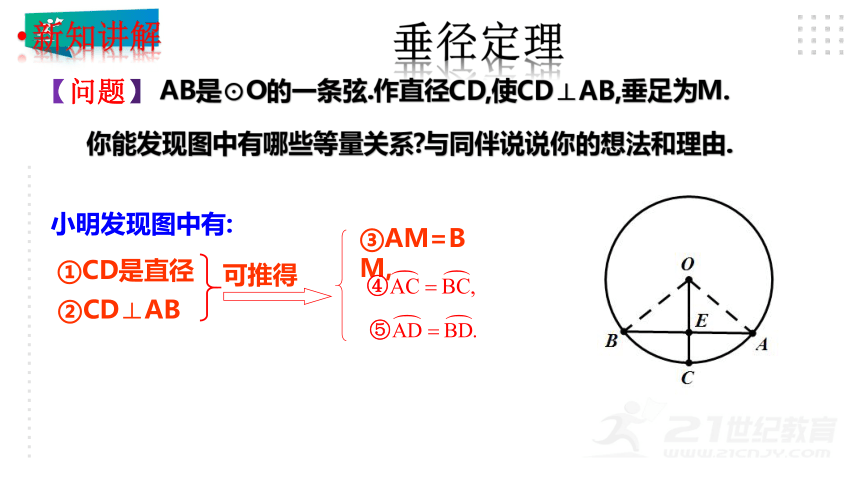
【问题】
AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
新知讲解
垂径定理
③AM=BM,
小明发现图中有:
①CD是直径
②CD⊥AB
可推得
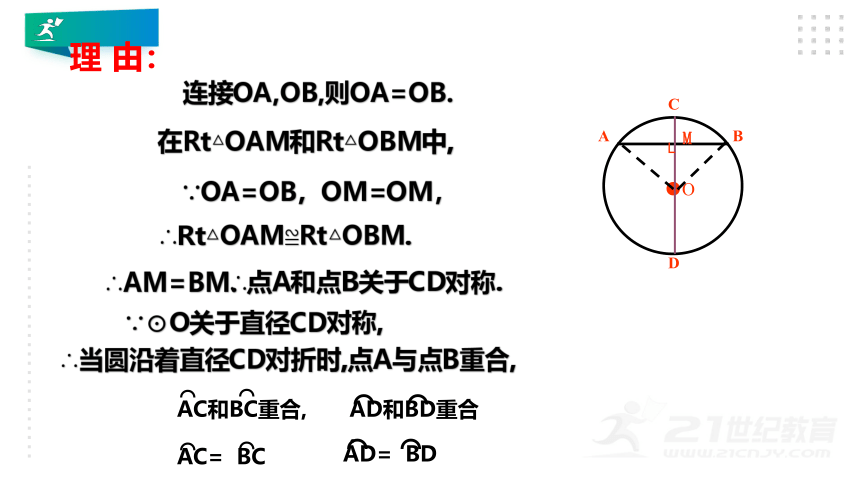
连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
理 由:
●O
A
B
C
D
└
M
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
AC= BC
⌒
⌒
AD= BD
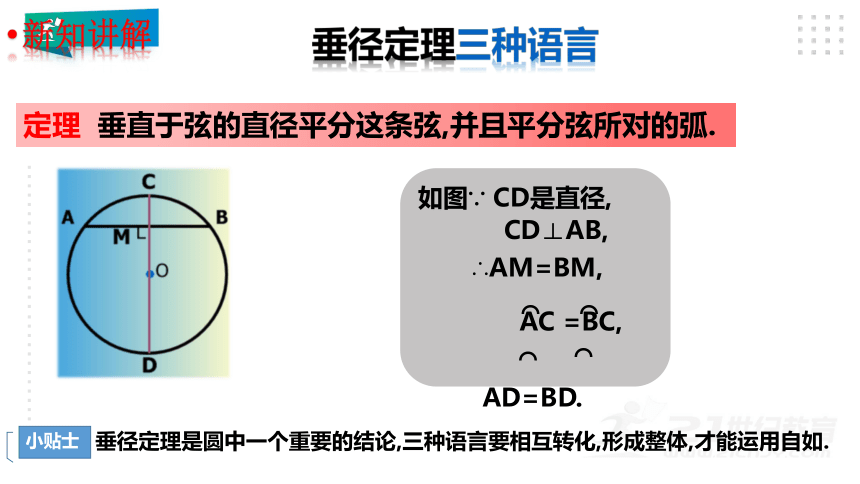
垂径定理三种语言
新知讲解
定理 垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
小贴士
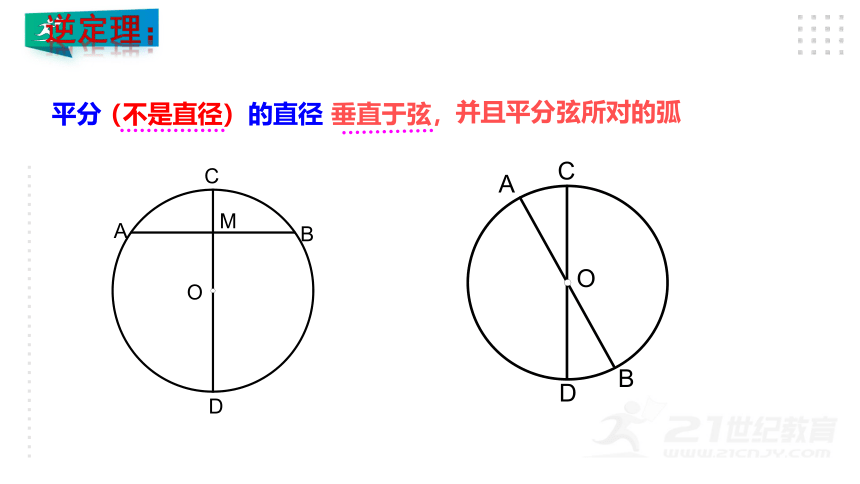
(不是直径)
并且平分弦所对的弧
平分
的直径
垂直于弦,
逆定理:
逆定理再思考
你可以写出相应的命题吗
相信自己是最棒的!
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC= BC,
⌒
⌒
⑤AD=BD.
D
河南中考弱化了关于“垂径定理”及相关推论的学习和考察!所以这项内容,老师们酌情使用.
参考
条件 结论 命题
①② ③④⑤
①③ ②④⑤
①④ ②③⑤
①⑤ ②③④ ②③ ①④⑤
②④ ①③⑤
②⑤ ①③④ ③④ ①②⑤
③⑤ ①②④ ④⑤ ①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
河南中考弱化了关于“垂径定理”及相关推论的学习和考察!所以这项内容,老师们酌情使用.
如图3-13,—条公路的转弯处是—段圆弧(即图中的弧CD).点O是弧CD所
在圆的圆心,其中CD=600m;E为弧CD上点,且OE⊥CD,垂足为F,EF=90m.
求这段弯路的半径.
解:如图,连接OC.
设弯路的半径为Rm,则OF=(R-90)m. 因为OE⊥CD.
根据勾股定理,得OC =CF2十OF2,即R =3002+(R-90) ,解得R=545. 所以这段弯路的半径为545 m.
典例精讲
【规律方法】 运用垂径定理及其推论解决一些数学问题.最常见的辅助线是连接圆上的点与圆心构成半径,及过圆心作弦的垂线,构造直角三角形,利用勾股定理解决问题.
归纳小结
口诀“连半径,做垂直”
1、“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问经几何?”用现在的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长.”依题意,CD长为( )
A.22.5寸 B.13寸
C.25寸 D.26寸
D
跟踪练习
口诀“连半径,做垂直”
2、如图,已知⊙O的半径为30mm,弦AB=36mm.则点O到AB的距离是 ,及 ∠OAB的余弦值= .
C
24cm
口诀“连半径,做垂直”
跟踪练习
1.如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,
CM = 4,求AB.
解:连接OA,
在⊙O中,直径CD⊥AB,
∴ AB =2AM,
△OMA是直角三角形.
∵ CD = 20,
∴ AO = CO = 10.
∴ OM = OC – CM = 10 – 4 = 6.
在Rt △OMA中,AO = 10,OM = 6,
根据勾股定理,得:AO2=OM2+AM2
∴ AB=2AM=2×8=16.
课堂练习
2.如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上.
你认为AC与BD的大小有什么关系?为什么?
课堂练习
G
└
解:作OG⊥AB,
∵AG=BG,CG=DG,
∴AC=BD.
3.如图,⊙O的直径为10,弦AB=8,P是AB上一个动点,则OP的最小值为( )
A.2 B.3 C.4 D.5
4.(2020·甘孜州)如图,AB为⊙O的直径,弦CD⊥AB于点H.若AB=10,CD=8,则OH的长度为 .
B
3
课堂练习
5.如图,在半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片,则弓形弦AB的长为( )
A.10 cm B.16 cm
C.24 cm D.26 cm
6.如图,水平放置的圆柱形排水管道的截面直径是1 m,其中水面的宽AB为0.8 m,则排水管内水的深度为 m.
C
0.8
课堂练习
7.如图,AB是⊙O的弦,点C在AB的延长线上,AB=2BC,连接OA,OC,若∠OAC=45°,则tanC的值为( )
A. 1 B. C. D.2
B
D
课堂练习
8.(襄阳·中考)已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A.17cm B.7 cm
C.12 cm D.17 cm或7 cm
图(1) 图(2)
D
课堂练习
1.圆的相关概念,弦、弧、优弧、劣弧.
3、通过对“垂径定理”及9条逆定理的探究,发展学生的思维和表达能力
2.垂径定理及推论、圆的对称性.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
§3.3 垂径定理
北师版九年级下册 圆
1.通过手脑结合,充分掌握圆的轴对称性.
2.运用探索、推理,充分了解圆中的垂径定理及其逆定理.
3.拓展思维,与实践相结合,运用垂径定理及其逆定理进行有关的计算和证明.并着重培养学生的数学语言表达能力.
温故知新
圆是轴对称图形吗?
如果是,它的对称轴是什么 你能找到多少条对称轴?
你是用什么方法解决上述问题的
●O
圆的对称轴是任意一条经过圆心的直线,
它有无数条对称轴.
圆的相关概念
新知讲解
大于半圆的弧叫做优弧,
小于半圆的弧叫做劣弧
连接圆上任意两点的线段叫做弦.
经过圆心的弦叫做直径.
直径是弦,但弦不一定是直径;
半圆是弧,但弧不一定是半圆;
半圆既不是劣弧,也不是优弧.
注意:
如图:优弧ADB 记作
一、劣弧、优弧
D
二、弦、直径
【问题】
AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
新知讲解
垂径定理
③AM=BM,
小明发现图中有:
①CD是直径
②CD⊥AB
可推得
连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
理 由:
●O
A
B
C
D
└
M
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
AC= BC
⌒
⌒
AD= BD
垂径定理三种语言
新知讲解
定理 垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
小贴士
(不是直径)
并且平分弦所对的弧
平分
的直径
垂直于弦,
逆定理:
逆定理再思考
你可以写出相应的命题吗
相信自己是最棒的!
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC= BC,
⌒
⌒
⑤AD=BD.
D
河南中考弱化了关于“垂径定理”及相关推论的学习和考察!所以这项内容,老师们酌情使用.
参考
条件 结论 命题
①② ③④⑤
①③ ②④⑤
①④ ②③⑤
①⑤ ②③④ ②③ ①④⑤
②④ ①③⑤
②⑤ ①③④ ③④ ①②⑤
③⑤ ①②④ ④⑤ ①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
河南中考弱化了关于“垂径定理”及相关推论的学习和考察!所以这项内容,老师们酌情使用.
如图3-13,—条公路的转弯处是—段圆弧(即图中的弧CD).点O是弧CD所
在圆的圆心,其中CD=600m;E为弧CD上点,且OE⊥CD,垂足为F,EF=90m.
求这段弯路的半径.
解:如图,连接OC.
设弯路的半径为Rm,则OF=(R-90)m. 因为OE⊥CD.
根据勾股定理,得OC =CF2十OF2,即R =3002+(R-90) ,解得R=545. 所以这段弯路的半径为545 m.
典例精讲
【规律方法】 运用垂径定理及其推论解决一些数学问题.最常见的辅助线是连接圆上的点与圆心构成半径,及过圆心作弦的垂线,构造直角三角形,利用勾股定理解决问题.
归纳小结
口诀“连半径,做垂直”
1、“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问经几何?”用现在的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长.”依题意,CD长为( )
A.22.5寸 B.13寸
C.25寸 D.26寸
D
跟踪练习
口诀“连半径,做垂直”
2、如图,已知⊙O的半径为30mm,弦AB=36mm.则点O到AB的距离是 ,及 ∠OAB的余弦值= .
C
24cm
口诀“连半径,做垂直”
跟踪练习
1.如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,
CM = 4,求AB.
解:连接OA,
在⊙O中,直径CD⊥AB,
∴ AB =2AM,
△OMA是直角三角形.
∵ CD = 20,
∴ AO = CO = 10.
∴ OM = OC – CM = 10 – 4 = 6.
在Rt △OMA中,AO = 10,OM = 6,
根据勾股定理,得:AO2=OM2+AM2
∴ AB=2AM=2×8=16.
课堂练习
2.如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上.
你认为AC与BD的大小有什么关系?为什么?
课堂练习
G
└
解:作OG⊥AB,
∵AG=BG,CG=DG,
∴AC=BD.
3.如图,⊙O的直径为10,弦AB=8,P是AB上一个动点,则OP的最小值为( )
A.2 B.3 C.4 D.5
4.(2020·甘孜州)如图,AB为⊙O的直径,弦CD⊥AB于点H.若AB=10,CD=8,则OH的长度为 .
B
3
课堂练习
5.如图,在半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片,则弓形弦AB的长为( )
A.10 cm B.16 cm
C.24 cm D.26 cm
6.如图,水平放置的圆柱形排水管道的截面直径是1 m,其中水面的宽AB为0.8 m,则排水管内水的深度为 m.
C
0.8
课堂练习
7.如图,AB是⊙O的弦,点C在AB的延长线上,AB=2BC,连接OA,OC,若∠OAC=45°,则tanC的值为( )
A. 1 B. C. D.2
B
D
课堂练习
8.(襄阳·中考)已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A.17cm B.7 cm
C.12 cm D.17 cm或7 cm
图(1) 图(2)
D
课堂练习
1.圆的相关概念,弦、弧、优弧、劣弧.
3、通过对“垂径定理”及9条逆定理的探究,发展学生的思维和表达能力
2.垂径定理及推论、圆的对称性.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
